Прямой изгиб. Лекция №6

1.

ЛЕКЦИЯ №6
1
ПРЯМОЙ ИЗГИБ

2.

ПРЯМОЙ ИЗГИБ
2
При изгибе возникают в общем случае изгибающие моменты Mx, My и
поперечные силы Qx , Qy.
Если в поперечном сечении возникает только один изгибающий момент
Mx, то такой изгиб называется чистым.
В большинстве случаев дополнительно к изгибающему моменту
возникает поперечная сила Qy, и такой изгиб называется поперечным.
Если внешняя нагрузка и реактивные усилия лежат в одной плоскости, то
такой изгиб называется плоским.
Прямые брусья, работающие на изгиб, называются балками.

3.

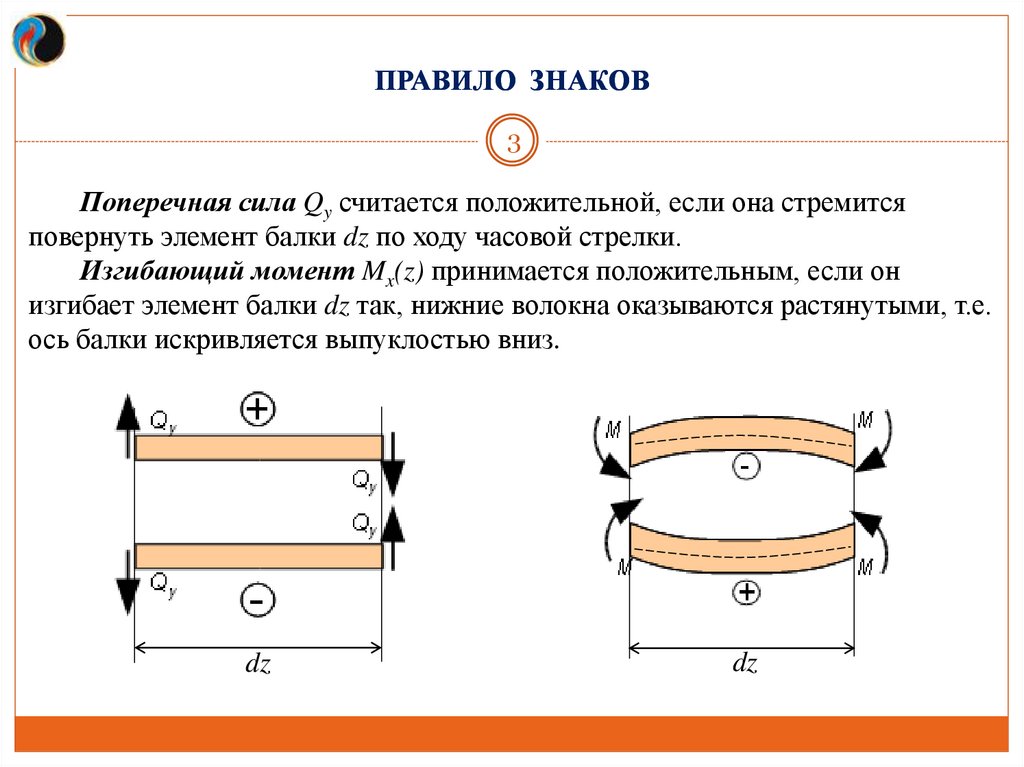
ПРАВИЛО ЗНАКОВ
3
Поперечная сила Qy считается положительной, если она стремится
повернуть элемент балки dz по ходу часовой стрелки.
Изгибающий момент Mx(z) принимается положительным, если он
изгибает элемент балки dz так, нижние волокна оказываются растянутыми, т.е.
ось балки искривляется выпуклостью вниз.
dz
dz

4.

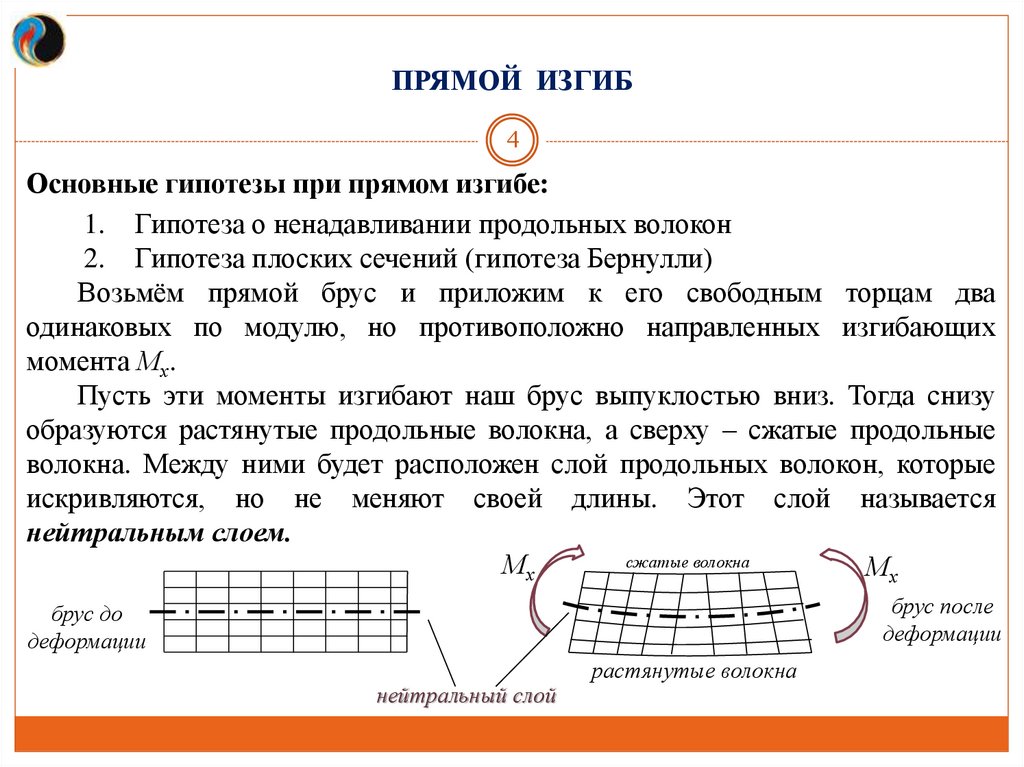
ПРЯМОЙ ИЗГИБ
4
Основные гипотезы при прямом изгибе:
1. Гипотеза о ненадавливании продольных волокон
2. Гипотеза плоских сечений (гипотеза Бернулли)
Возьмём прямой брус и приложим к его свободным торцам два
одинаковых по модулю, но противоположно направленных изгибающих
момента Мх.
Пусть эти моменты изгибают наш брус выпуклостью вниз. Тогда снизу
образуются растянутые продольные волокна, а сверху – сжатые продольные
волокна. Между ними будет расположен слой продольных волокон, которые
искривляются, но не меняют своей длины. Этот слой называется
нейтральным слоем.
сжатые волокна
Мх
Мх
брус после
деформации
брус до
деформации
нейтральный слой
растянутые волокна

5.

ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ
5
y
Дифференциальные зависимости при
изгибе связывают внутренние усилия между
собой в сечении и нагрузкой.
Выделим из балки элемент длиной dz,
находящийся
по
действием
внешней
вертикальной равномерно распределенной
нагрузкой
q,
и
заменим
действие
отброшенных частей внутренними усилиями.
qy
Mx Qy
Mx+dMx
O
z
Qy+dQy
dz
Выделенный элемент находится в равновесии и удовлетворяет уравнения
равновесия:
Y 0; Q q dz (Q dQ ) 0;
i
y
y
M 0i 0; - M x q y dz
y
y
dz
(Q y dQ y )dz ( M x dM x ) 0.
2

6.

ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ
6
Из первого уравнения получаем:
dQ y
q y
dz
Производная от поперечной силы по
продольной координате равна
интенсивности распределенной
нагрузки.
Из второго уравнения, пренебрегая
малыми второго порядка, получаем:
dM x
Qy
dz
Производная от изгибающего
момента по продольной координате
равна поперечной силе.
Полученные дифференциальные зависимости называются
теоремой Журавского.
С использованием этих основных зависимостей получаем:
d 2M x
q y
2
dz
Вторая производная от изгибающего момента по продольной координате
равна интенсивности распределенной нагрузки.

7.

ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ
7
Дифференциальные зависимости при изгибе применяются для контроля
правильности построения эпюр поперечных сил и изгибающих моментов.
Зависимости между qy, Qy и Mx можно представить в интегральной форме.
Q y q y dz
M x Q y dz
z
z
Они применяются для определения поперечной силы и изгибающего
момента при любом способе задания распределенной нагрузки.

8.

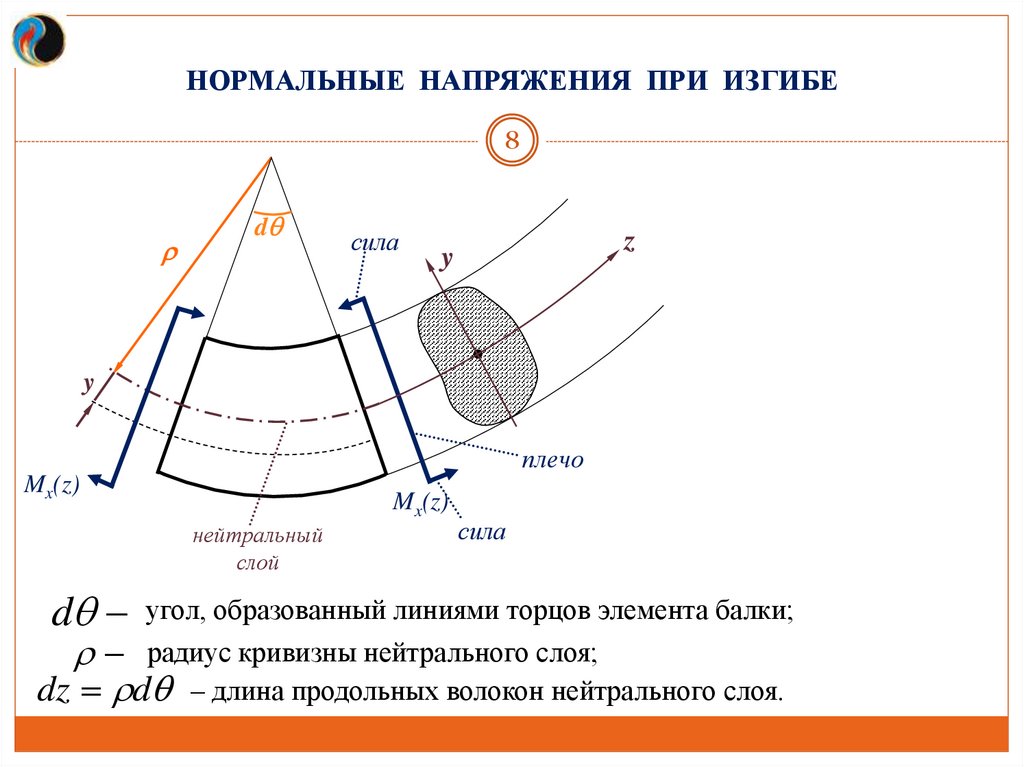
НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
8
d
сила
z
y
y
плечо
Mx(z)
Mx(z)
нейтральный
слой
сила
d угол, образованный линиями торцов элемента балки;
радиус кривизны нейтрального слоя;
dz d – длина продольных волокон нейтрального слоя.

9.

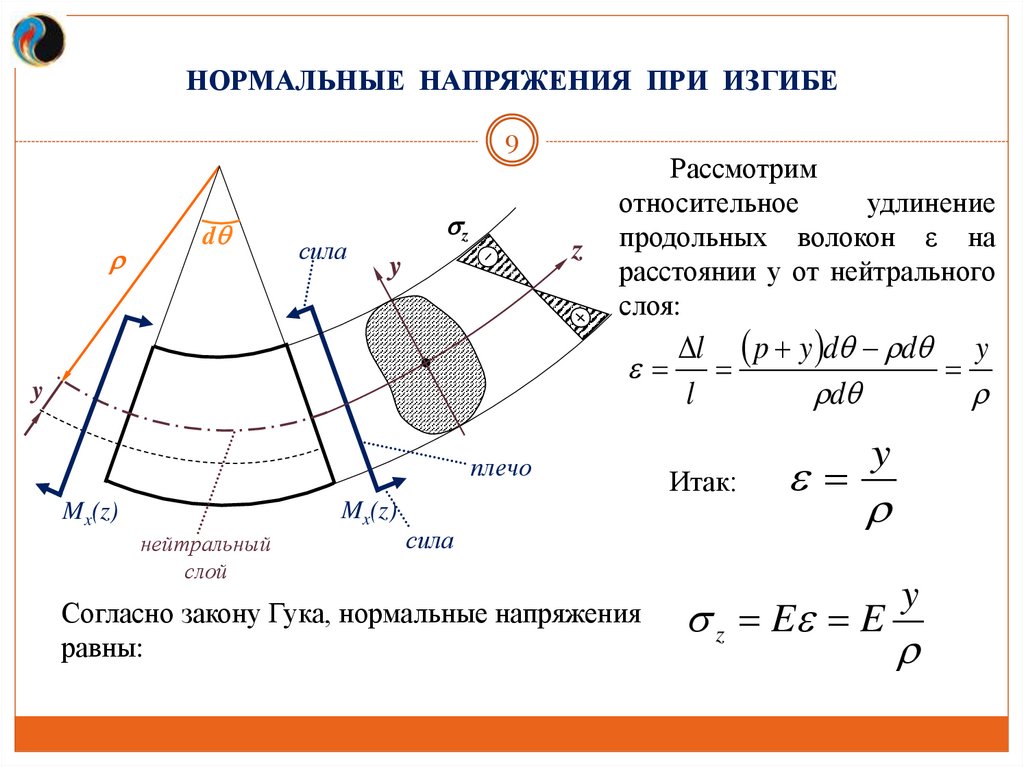
НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
9
d
сила
z
z
y
Рассмотрим
относительное
удлинение
продольных волокон ε на
расстоянии у от нейтрального
слоя:
l p y d d y
l
d
y
плечо
Mx(z)
Mx(z)
нейтральный
слой
сила
Согласно закону Гука, нормальные напряжения
равны:
Итак:
y
z E E
y

10.

НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
10
2
EJ x
Ey
E 2
Изгибающий момент равен: M ydF
x
F z
F dF F y dF
Итак:
Mx
EJ x
Полученная формула выражает закон Гука при изгибе:
E
M xE
Mxy
Поэтому: z y
y
EJ x
Jx
Mxy
z
Jx
Mx
EJ x
1
(EJx – изгибная жесткость)
Размерность: [Н·м2]
Полученная зависимость называется
формулой Навье.

11.

НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
11
Максимальное нормальное напряжение в площади поперечного сечения
балки наблюдается на её поверхности и равно:
Mx
Mx
z max
ymax
Jx
Wx
Итак, получено:
Mx
z max
Wx
- «зеркальная» формула.
Опасным сечением при изгибе называется поперечное сечение бруса, в
котором возникает максимальное нормальное напряжение.

12.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
12
а) проверочный расчет – определяется максимальное расчетное напряжение
и сравнивается с допускаемым напряжением:
max
M x max
Wx
б) проектный расчет – подбор сечения бруса производится из условия:
Wx
M xma x
в) определение допускаемой нагрузки – допускаемый изгибающий момент
определяется из условия:
M x Wx
Далее по полученному значению [Mx] определяют допускаемые значения
внешних поперечных нагрузок [Qy] и внешних изгибающих моментов [M внеш].
Условие прочности имеет вид: Q≤[Q], Mвнеш≤[Mвнеш].

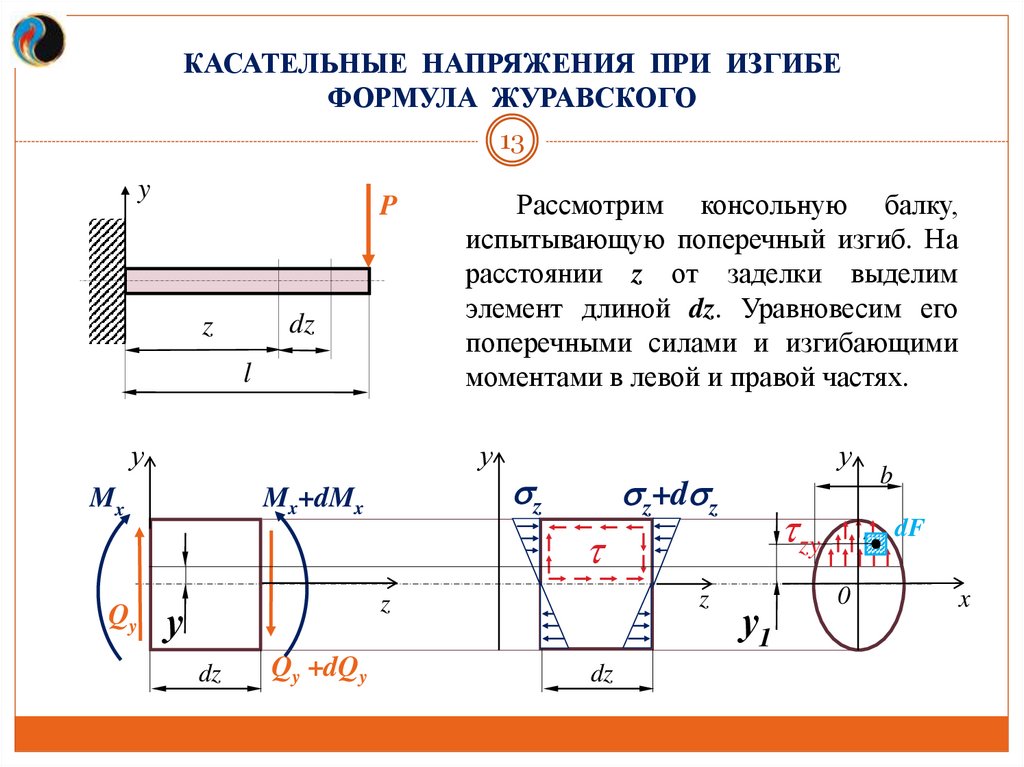
13.

КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ
ФОРМУЛА ЖУРАВСКОГО
13
y
P
dz
z
l
у
Рассмотрим консольную балку,
испытывающую поперечный изгиб. На
расстоянии z от заделки выделим
элемент длиной dz. Уравновесим его
поперечными силами и изгибающими
моментами в левой и правой частях.
у
Mx
Mx+dMx
z
у
z+d z
zy
Qy
z
z
у
dz
Qy +dQy
dz
у1
b
dF
0
x

14.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
14
zy
y
z
b
zy
x
N*+dN*
N* y
yz
0
dz
Продольным
горизонтальным
сечением на расстоянии у от
нейтрального
слоя
разделим
выделенный элемент на две части.
Рассмотрим равновесие верхней части,
имеющей основание шириной b. С учетом
закона парности касательных напряжений
получаем, что в поперечном сечении равны в
продольном сечении, направлены друг от друга
по перпендикуляру.

15.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
15
Составим уравнение Fi z 0 учитывая, что действию всех сил должны
противодействовать обратные:
F
z
N
N
dN
yzbdz 0
i
или
dN
yz
(1)
bdz
dN yz bdz
Mx
Mx
Mx
N dF
y1dF
y1dF
Sx ,
Jx
J x F
Jx
F
F
dM x
M
dN
S x (2)
N x S x
Jx
Jx
dM x S x Qy S x
Подставим (2) в (1): yz
J xbdz
J xb

16.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
16
Полученная зависимость называется формулой Журавского:
yz
Q y S x
J xb
Где:
Qy – поперечная сила, [H];
Sx* – статический момент отсеченной части сечения, находящейся выше (или
ниже) некоторой характерной точки, [м3];
b – ширина сечения в некоторой характерной точке, [м];
Jx – момент инерции всего сечения относительно центра тяжести, [м4].
Характерными будем считать точки на оси ординат, располагающиеся по
верхней и нижней образующей сечения, в местах изменения его ширины, а также в
центре тяжести сечения.
Sx F y
Где:
F* – площадь части сечения выше (или ниже) характерной точки, [м2];
у* – расстояние от центра тяжести площади F* до центра тяжести сечения, [м];

17.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
17
Для стержня прямоугольного сечения со сторонами b и h в общем случае для
0 y
h
2
имеем:
h
y
h
2
y b h y h y y b h y h y
S x F * y b y
2
2
2
4
2
2
4
2
h 2 hy hy y 2
h2 y 2 b h2
b
y 2
b
4
4
2
2 2 4
8
8

18.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
18
Вывод из формулы Журавского:
зависимость τ от у в сечении определяется величиной статического
момента Sx*, поэтому, независимо от формы поперечного сечени:
τmax достигается в центре его тяжести, т.к. в нем Sx*=max, т.к. F*=max
τ=0 в верхней и нижней точках по высоте сечения, т.к. в них Sx*=0, т.к.
F*=0 выше и ниже характерных точек по верхней и нижней образующим
сечения.
Касательные напряжения, возникающие в брусе при
поперечном изгибе, обычно на порядок меньше нормальных
напряжений, поэтому в упрощенных расчетах стальных
балок на прочность ими пренебрегают.

19.

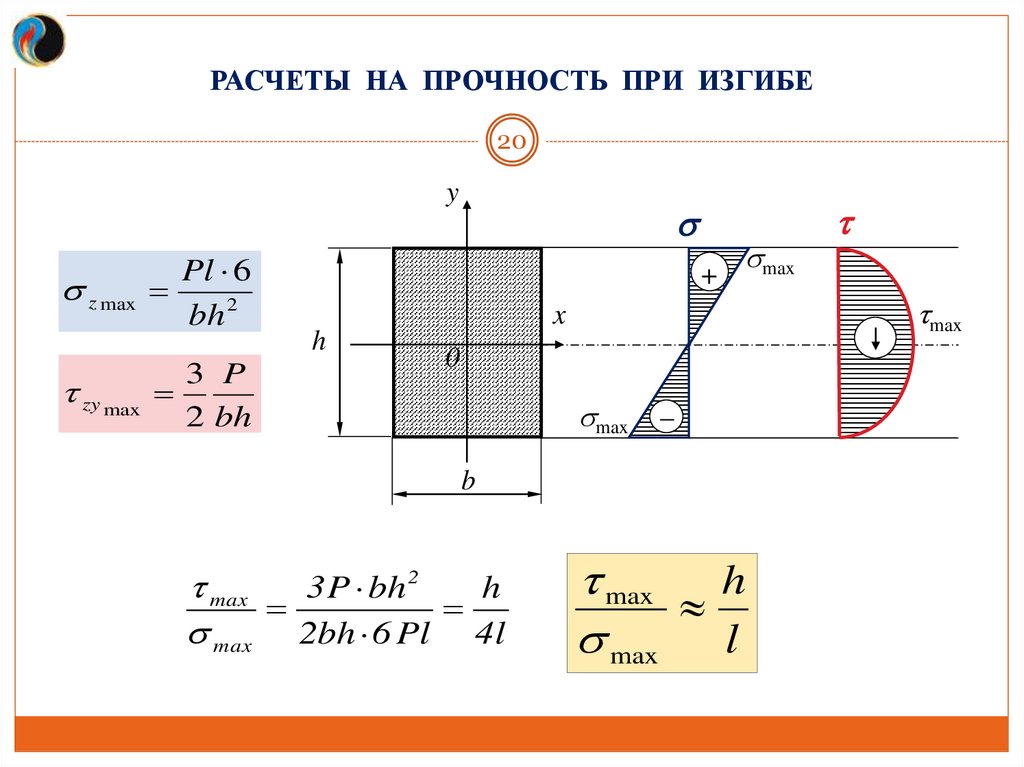
РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
19
Определим различие уровня величин нормальных и касательных напряжений
для консольной балки прямоугольного сечения.
Р
Опасное сечение – заделка:
l
M x max Pl
Q P
Нормальные напряжения (формула Навье):
Q
+
Р
M
Рl
z max
M x max
Wx
Pl 6
bh 2
Касательные напряжения (формула Журавского):
_
h h
P b
Р S x
3 P
2
4
zy max
3
bh
Jx b
2 bh
b
12

20.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ
20
y
Pl 6
z max
bh 2
3 P
zy max
2 bh
+
max
max
x
h
0
max
_
b
max
3 P bh 2
h
max 2bh 6 Pl 4l
max
h
max l

21.

РАБОТА НА ПОПЕРЕЧНЫЙ ИЗГИБ ЛИСТОВ В ПАКЕТАХ
21
нескрепленный пакет листов
Р
n – число листов в пакете
hi – высота одного листа
h
l
max
b
Р
h
hi
n
Р
Рi - сила, воспринимаемая одним листом;
n
Рl - момент, возникающий в одном листе;
Mi
n
2
bh
b h - момент
Wxi
сопротивления сечения,
6
6 n возникающий в одном
2
i
листе.

22.

РАБОТА НА ПОПЕРЕЧНЫЙ ИЗГИБ ЛИСТОВ В ПАКЕТАХ
22
M i Pl 6 n 2 6 Pl
max
2 n
2
Wxi
n bn
bh
- максимальное напряжение,
возникающее в нескрепленном
пакете листов.
1 M i Pl 12 n 3 12 Pl 2
k
n - кривизна листового пакета
3
3
EJ xi n E bh
Ebh
3
b h
J xi - момент инерции одного листа
12 n

23.

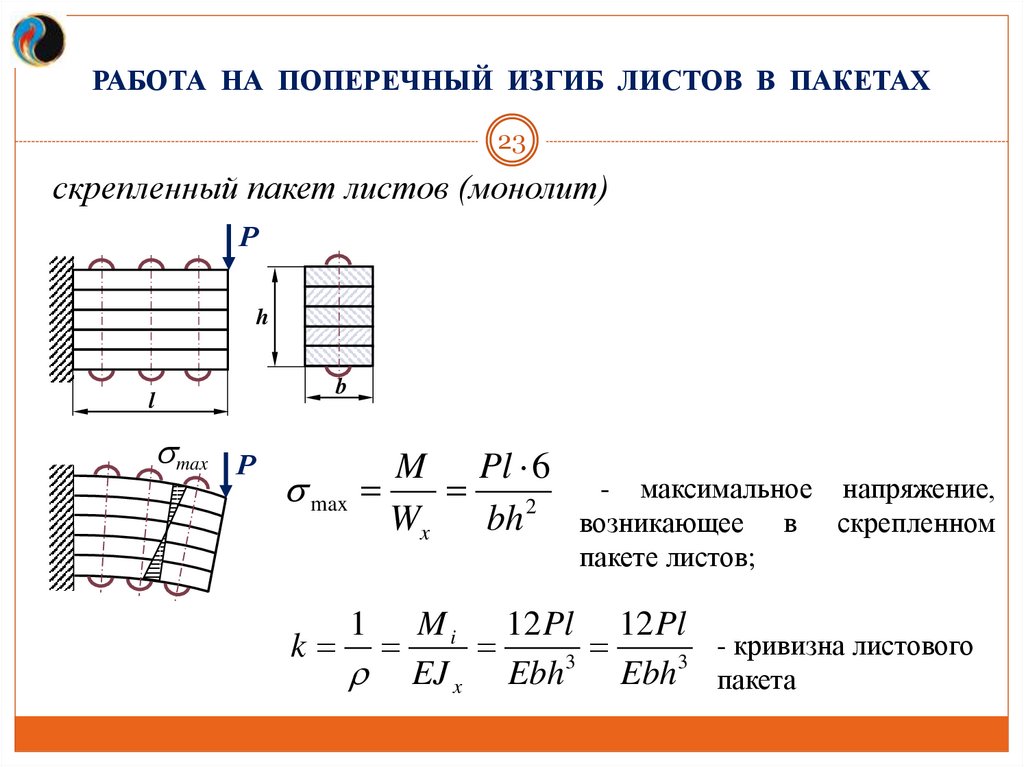
РАБОТА НА ПОПЕРЕЧНЫЙ ИЗГИБ ЛИСТОВ В ПАКЕТАХ
23
скрепленный пакет листов (монолит)
Р
h
b
l
max
Р
M Pl 6
max
Wx
bh 2
- максимальное напряжение,
возникающее в скрепленном
пакете листов;
M i 12 Pl 12 Pl
- кривизна листового
k
3
3
EJ x Ebh
Ebh пакета
1

24.

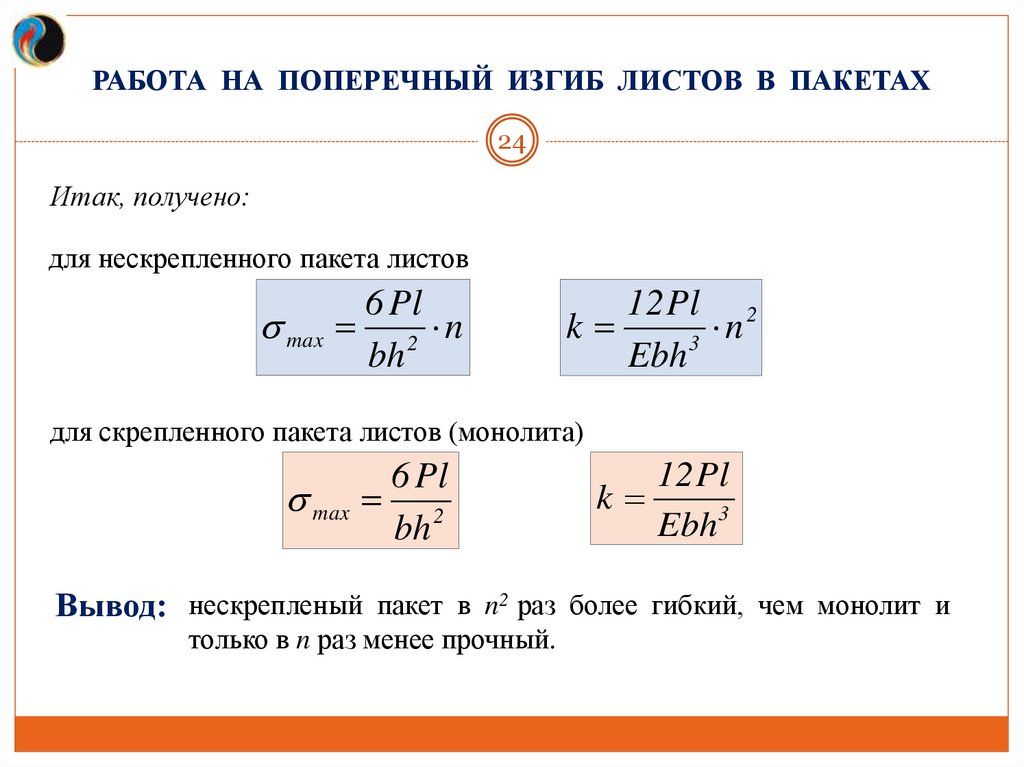
РАБОТА НА ПОПЕРЕЧНЫЙ ИЗГИБ ЛИСТОВ В ПАКЕТАХ
24
Итак, получено:
для нескрепленного пакета листов
6 Pl
max 2 n
bh
12 Pl 2
k
n
3
Ebh
для скрепленного пакета листов (монолита)
6 Pl
max 2
bh
12 Pl
k
Ebh3
Вывод: нескрепленый пакет в n2 раз более гибкий, чем монолит и
только в n раз менее прочный.

25.

РАЦИОНАЛЬНЫЕ ТИПЫ СЕЧЕНИЙ БАЛОК
25
Спроектировать балку рационального сечения означает задать ей такие
размеры и форму, которые обеспечат при минимальном расходе материала
выполнение условия прочности.
Несущая способность балки пропорциональна моменту сопротивления
сечения, т.е. [Mx]=[Wx], а расход материала – площади поперечного сечения.
Чем меньше площадь поперечного сечения балки, тем она легче
и, соответственно, экономичнее.
Показателем рациональности сечения балки является коэффициент
экономичности, определяемый по формуле:
Wx
F h
Чем выше , тем экономичнее сечение.

26.

РАЦИОНАЛЬНЫЕ ТИПЫ СЕЧЕНИЙ БАЛОК
26
В
строительной
промышленности
используются
следующие
тонкостенные стандартные прокатные профили поперечных сечений:
равнополочные и
неравнополочные
уголки
равнополочные и
неравнополочные
двутавры верхняя горизонтальная
швеллеры
полка
вертикальная
стенка
нижняя горизонтальная
полка
Стандартные профили регламентированы по ГОСТ и сведены в сортаменты.

27.

РАЦИОНАЛЬНЫЕ ТИПЫ СЕЧЕНИЙ БАЛОК
27
Пример Определить, какое из представленных сечений является
наиболее рациональным для стальной балки ([ ] = 160 МПа)
консольного типа, нагруженной согласно рисунку.
q
l
Qy
ql2/2
ql 2 5 103 4
M x max
40кН / м
2
2
2
+
ql
Mx
l=4м
q = 5 kH/м
Опасное сечение – жесткая заделка:
–
Условие прочности:
Mx
z max
Wx

28.

РАЦИОНАЛЬНЫЕ ТИПЫ СЕЧЕНИЙ БАЛОК
28
y
прямоугольное сечение
M x 12
bh 2 h h 2 h 3
Wx
3
6
2 6 12
h
h 3
12 M x
3
h
x
0
Примем h=2b
b
12 40 10
0 ,144 м 14 ,4см - требуемая высота сечения
6
160 10
3
h
h 2 0 ,144
F bh h
1,0368 10 2 м 2 103,68см 2 - площадь сечения
2
2
2
2
h 3 0 ,144
Wx
248 ,33см 3
12
12
3
- момент сопротивления сечения
Wx
248 ,33
0 ,166 - коэффициент экономичности сечения
F h 103,68 14 ,4

29.

РАЦИОНАЛЬНЫЕ ТИПЫ СЕЧЕНИЙ БАЛОК
29
круглое сечение
d 3
M x 32
Wx
3
32
d
x
0
d
3
32
40
10
d 3
3
0 ,136 м 13,6 см
6
3,14 160 10
32 M x
y
- требуемая высота сечения
3,14 0,136
F
0, 01452 10 2 м2 145, 2см2 - площадь сечения
4
4
d2
2
d 3 3,14 0 ,136 3
Wx
246 ,83см 3 - момент сопротивления сечения
32
32
Wx
246 ,83
0 ,125
F h 145 ,2 13,6
- коэффициент экономичности сечения

30.

РАЦИОНАЛЬНЫЕ ТИПЫ СЕЧЕНИЙ БАЛОК
30
y
двутавровое сечение
40 10 3
3 3
3
Wx
0
,
25
10
м
250
см
160 106
- требумый момент сопротивления сечения
Mx
h
0
x
b
Ближайший момент сопротивления сечения по сортаменту Wx = 254 см3, что
соответствует двутавру № 22 «а».
Его характеристики: F = 32,8 см2, h = 22 см.
Wx
254
0 ,352 - коэффициент экономичности сечения
F h 32 ,8 22
Итак, получено:
αпрямоуг. = 0,166
αкруг. = 0,125
αдвут. = 0,352
Вывод:
Наиболее предпочтительным оказалось
двутавровое сечение, т.к. его коэффициент
экономичности максимален.