Векторы и операции над ними (часть 1). ЕГЭ по математике

1.

2.

Справочный материал
Координаты вектора
А х1; у1
В х2 ; у2
у2
АВ х2 х1; у2 у1
А
а а1; а2
а а а
2
1
В
2
2
х1
у1
х2

3.

Справочный материал
Сложение векторов
а а1; а2
b b1; b2
а b а1 b1; а2 b2
Свойства :
Сумма векторов – вектор.
1) а 0 а
2) а b b а
3) а b c а b c

4.

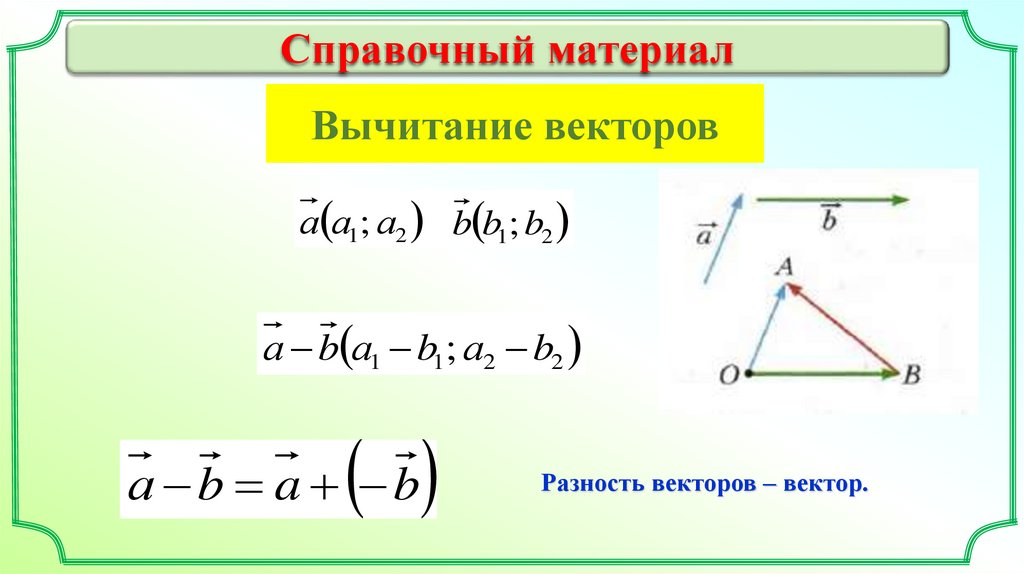
Справочный материал
Вычитание векторов
а а1; а2 b b1; b2
а b а1 b1; а2 b2
а b a b
Разность векторов – вектор.

5.

Справочный материал
Скалярное произведение векторов
Скалярное произведение векторов – число.
Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
а а1; а2 b b1; b2
a b = a b cos(a b )
Для вычисления скалярного произведения
векторов существуют разные формулы.
Формула вычисления скалярного
произведения векторов через координаты
векторов не содержит косинуса угла.

6.

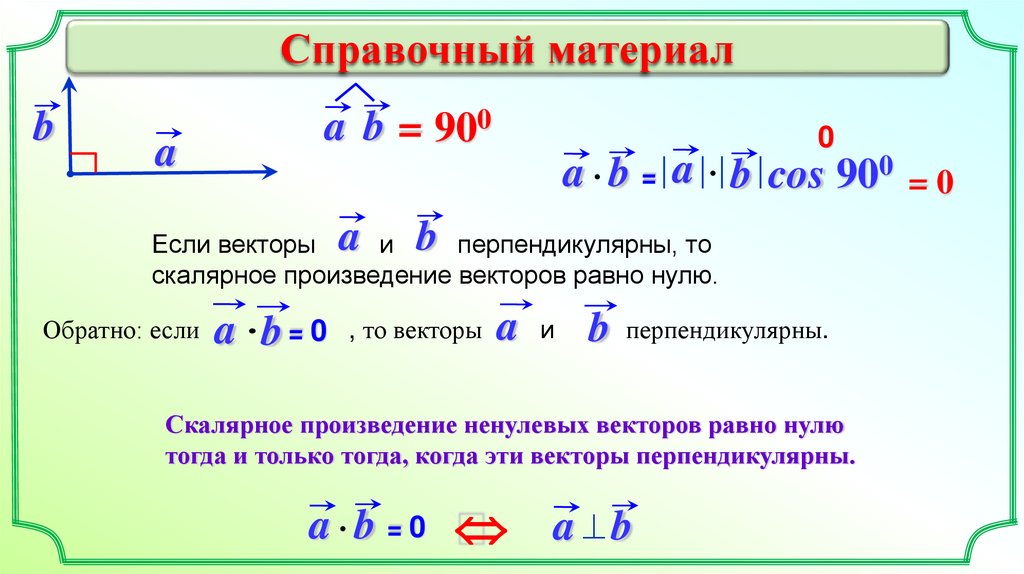
Справочный материал
b
a
a b = 900
a
0
a b = a b cos 900 = 0
b
Если векторы
и
перпендикулярны, то
скалярное произведение векторов равно нулю.
Обратно: если
a b = 0 , то векторы a и b перпендикулярны.
Скалярное произведение ненулевых векторов равно нулю
тогда и только тогда, когда эти векторы перпендикулярны.
a b =0
a ^b

7.

Справочный материал
a b < 900
>0
a b = a b cos a > 0
b
a
Скалярное произведение ненулевых векторов
положительно тогда и только тогда , когда угол между
векторами острый.
a b > 0 a b < 900

8.

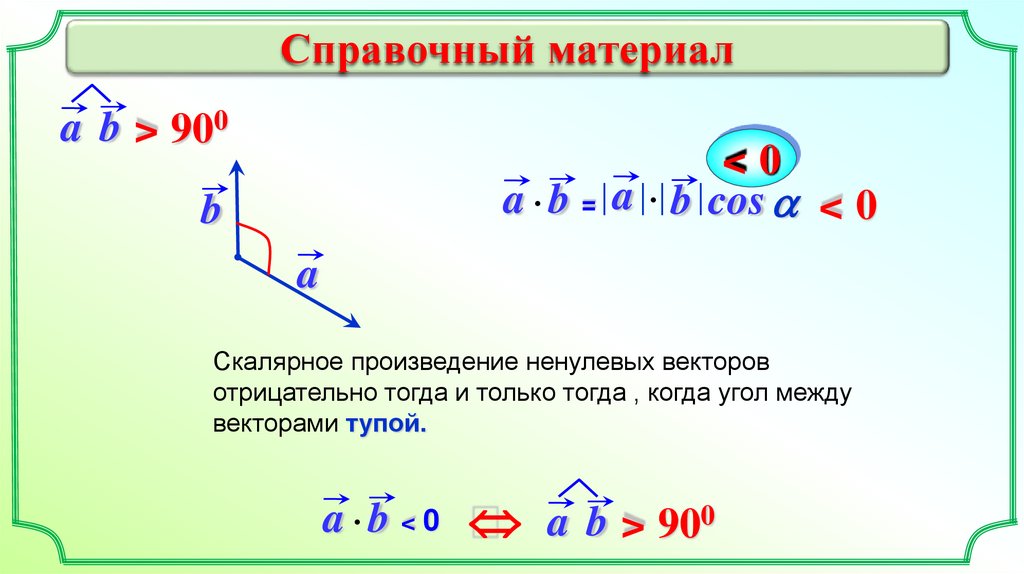
Справочный материал
a b > 900
<0
a b = a b cos a < 0
b
a
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда , когда угол между
векторами тупой.
a b < 0 a b > 900

9.

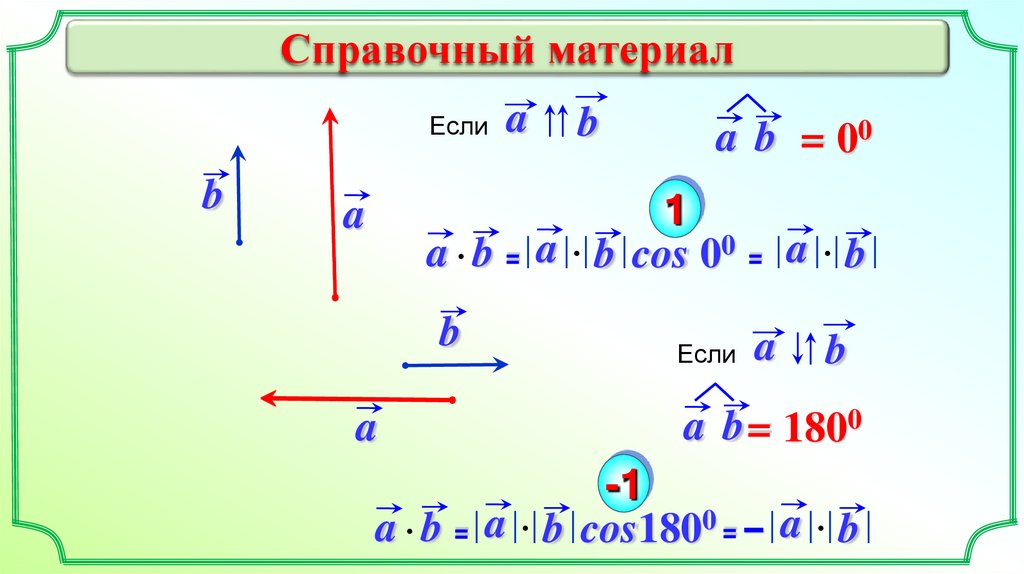
Справочный материал
Если
b
a
b
a b = 00
1
a b = a b cos 00 = a b
a
b
a
Если
a
b
a b = 1800
-1
a b = a b cos1800 = – a b

10.

Справочный материал
a
a a = 00
1
a a = a a cos 00 = a a = a 2
a a называется
скалярным квадратом вектора a и обозначается a 2
Скалярное произведение
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
a2 = a 2

11.

№1
Найдите длину вектора а (6; 8).
⃗

12.

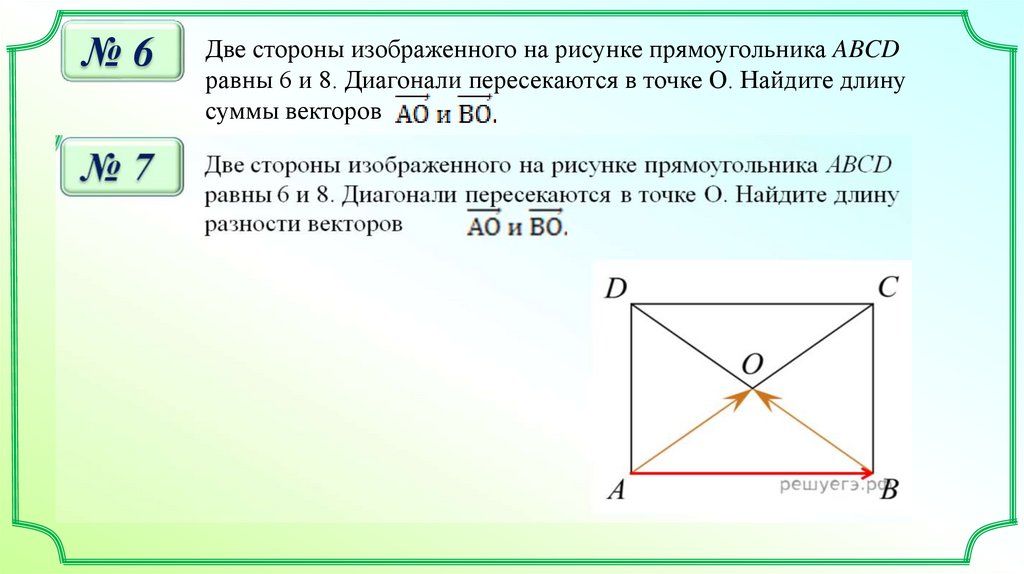
№6
Две стороны изображенного на рисунке прямоугольника ABCD
равны 6 и 8. Диагонали пересекаются в точке О. Найдите длину
суммы векторов

13.

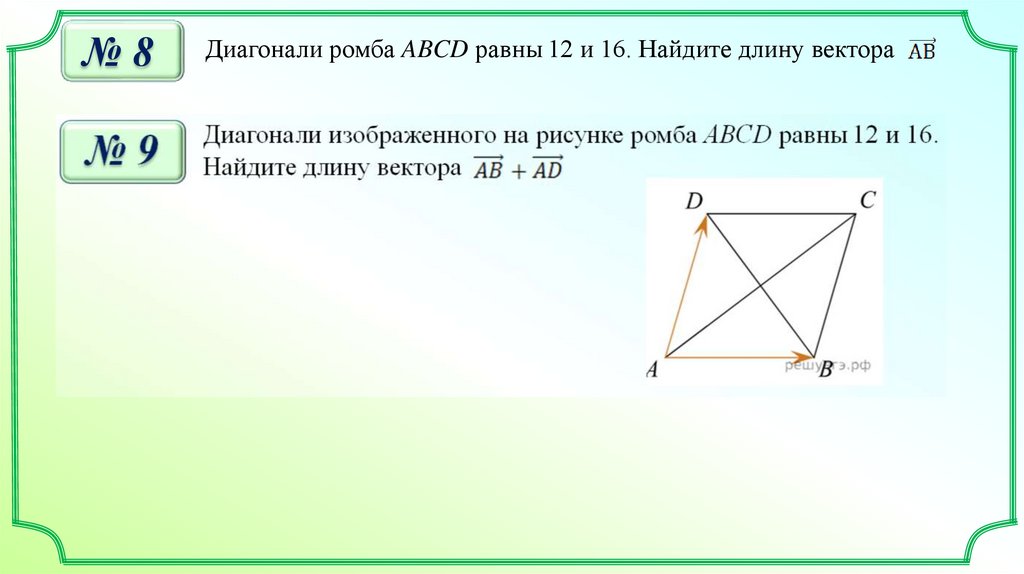
№8
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора

14.

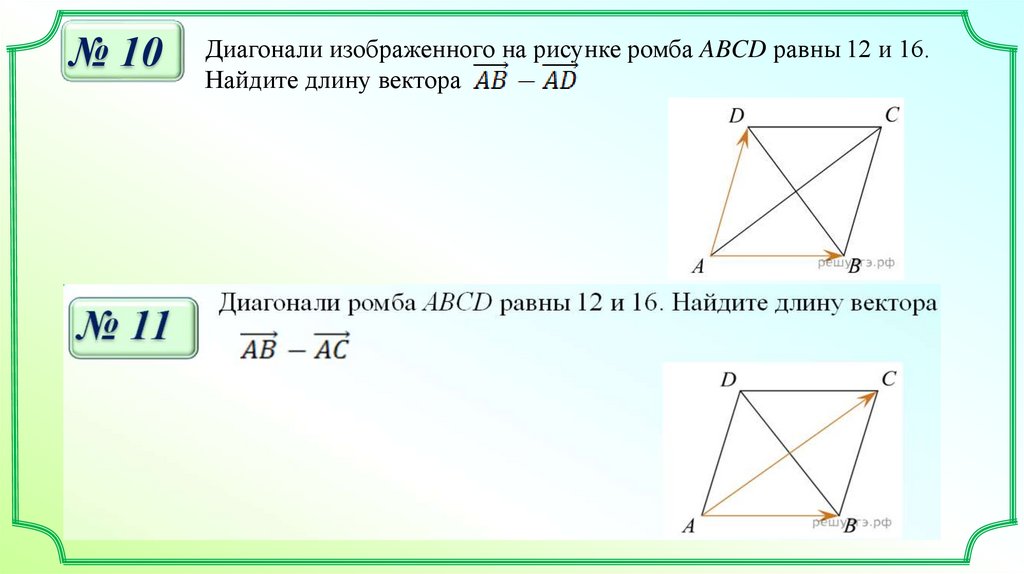
№ 10
Диагонали изображенного на рисунке ромба ABCD равны 12 и 16.
Найдите длину вектора

15.

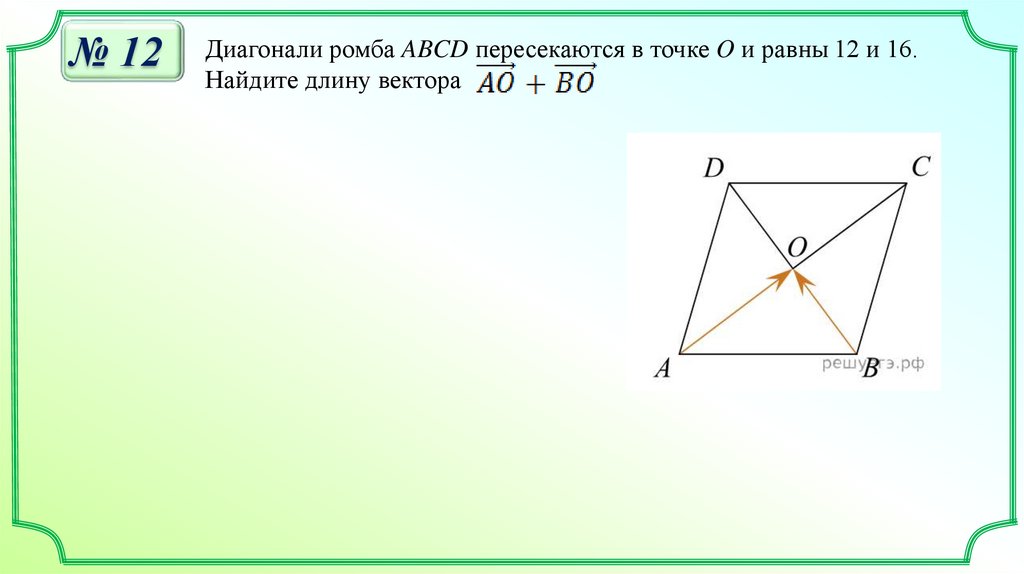
№ 12
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16.
Найдите длину вектора

16.

№ 13
Диагонали ромба ABCD пересекаются в точке О и равны 12 и 16.
Найдите длину вектора

17.

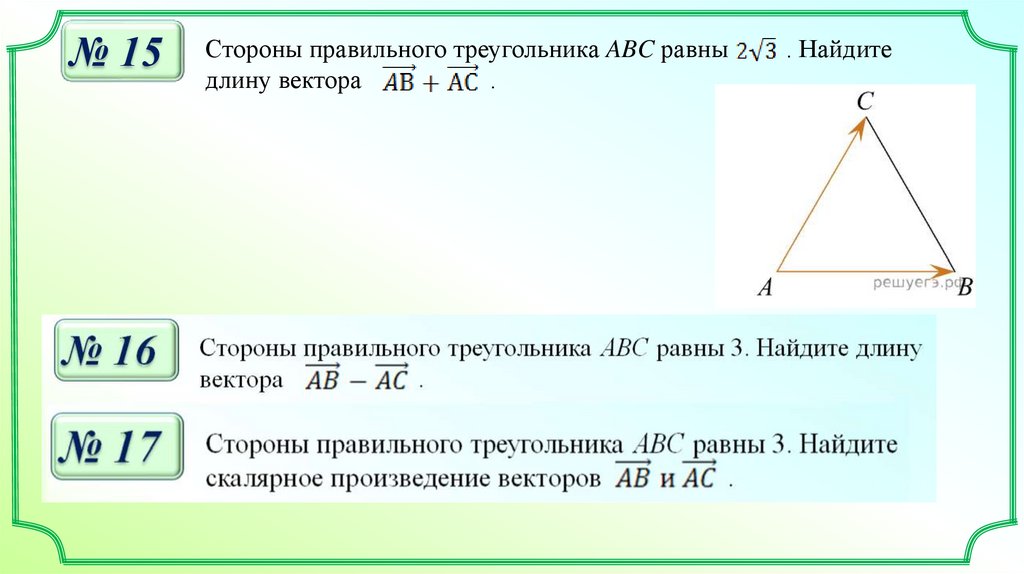
№ 15
Стороны правильного треугольника ABC равны
длину вектора
.
. Найдите

18.

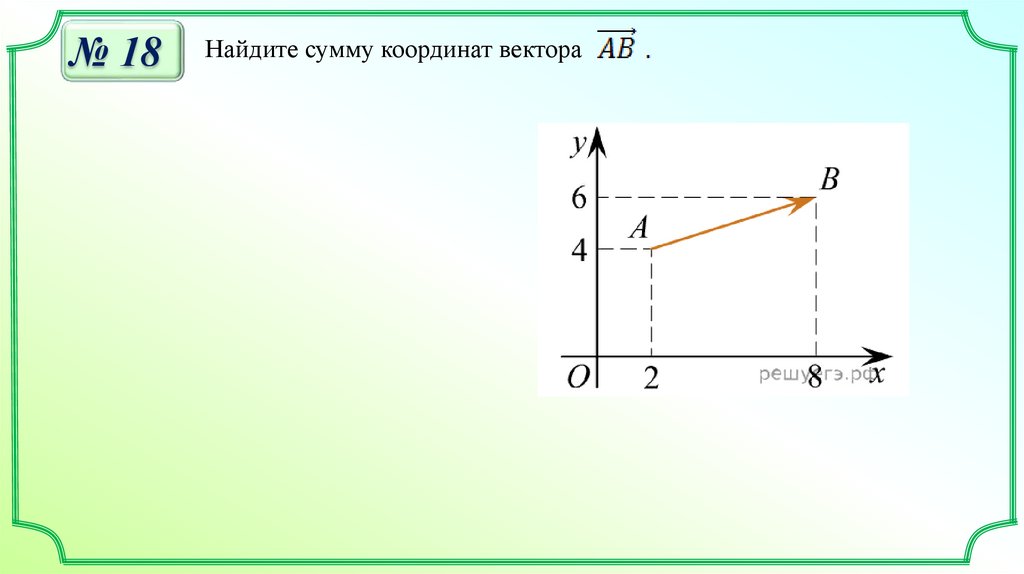
№ 18
Найдите сумму координат вектора

19.

№ 19
Вектор
с началом в точке A(2; 4) имеет координаты (6; 2).
Найдите абсциссу точки B.