Согласованный фильтр

1. ОПТИМАЛЬНЫЕ ЛС (продолжение)

2. ОСНОВНЫЕ ЭТАПЫ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ ЛС (предыдущая лекция)

1. Априорная информация в виде математических моделей
[ ], X (t ), N (t ).
2. Критерии оптимальности (качества ).
3. Ограничения на синтез ОС.
4. Синтез ОС.
5. Анализ ОС.
6. Точная или приближенная реализация ОС.

3. СОГЛАСОВАННЫЙ ФИЛЬТР

4. ФИЛЬТР, МАКСИМИЗИРУЮЩИЙ ОТНОШЕНИЕ СИГНАЛ/ШУМ (СОГЛАСОВАННЫЙ ФИЛЬТР)

1. Априорная информация
Наблюдаемый сигнал: Y (t ) sвх (t ) Nвх (t )
sвх (t ) - детерминированный сигнал
Nвх (t ) - белый шум с КФ
2. Критерий оптимальности:
N0
Kn ( )
( )
вх
2
2
s
2
вых (t0 )
q
max
hcф ( )
Dn
вых
3. Ограничения на синтез ОС: каузальный линейный фильтр с
постоянными параметрами
КЧХ фильтра
ИХ фильтра
Hсф ( f ) Cсф ( f )exp( j сф ( f ))
hcф ( ) 0 при 0

5. СИНТЕЗ СОГЛАСОВАННОГО ФИЛЬТРА

Спектральная плотность входного сигнала:
Sвх ( f ) F{sвх (t )} Sвх ( f )exp( j вх ( f ))
Спектральная плотность выходного сигнала:
Sвых ( f ) Hcф ( f )Sвх ( f ) Ccф ( f ) Sвх ( f ) exp( j ( вх ( f ) cф ( f )))
Сигнал на выходе фильтра:
sвых (t ) F 1 Sвых ( f )
Ccф ( f )Sвх ( f ) exp( j ( вх ( f ) cф ( f ) 2 ft ))df

6. СИНТЕЗ СОГЛАСОВАННОГО ФИЛЬТРА

Сигнал на выходе фильтра при t=t0:
sвых (t0 ) Ccф ( f ) Sвх ( f )exp( j ( вх ( f ) cф ( f ) 2 ft0 ))df
N0 2
Ccф ( f )df
Дисперсия шума на выходе фильтра: Dnвых
2
2
s
2
вых (t0 )
q
max
Hcф ( f )
Dn
вых
1. cф ( f ) вх ( f ) 2 ft0
2. Ccф ( f ) BSвх ( f )
B 0

7.

СИНТЕЗ СОГЛАСОВАННОГО
ФИЛЬТРА
КОМПЛЕКСНАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКА
ОПТИМАЛЬНОГО ФИЛЬТРА (СФ)
Hcф ( f ) BSвх ( f ) exp( j ( вх ( f ) 2 ft0 ))
BSвх ( f ) exp( j вх ( f )) exp( j 2 ft0 )
*
BSвх ( f )exp( j 2 ft0 )
ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА СФ
hсф (t ) F 1{Hсф ( f )} Bsвх (t0 t )
t0 tc

8. ВЫВОДЫ ПО РЕЗУЛЬТАТАМ СИНТЕЗА

*
Hcф ( f ) BSвх
( f )exp( j 2 ft0 )
hсф (t ) Bsвх (t0 t )
t0 tc
1. Спектральная плотность выходного сигнала
2
Sвых ( f ) BSвх
( f )exp( j 2 ft0 )
вых ( f ) 2 ft0
Компенсируются начальные фазы
в спектре входного сигнала
2. СФ является оптимальным для всех
сигналов одной и той же формы, т.е.
отличающихся от сигнала только
постоянным множителем
3.Если sвх(t) – четная функция относительно tc/2
hсф(t)=B sвх(t)
B 0
- вх(f)
вых(f) при t0=0
f
вх(f)
вых(f)

9. АНАЛИЗ СОГЛАСОВАННОГО ФИЛЬТРА

Сигнал на выходе СФ
2
Sвых ( f ) BSвх
( f )exp( j 2 ft0 )
2
sвых (t ) F 1 Sвых ( f ) B Sвх
( f ) exp( j 2 f (t0 t ))df
sвых (t ) B s (t t0 )
вх
1. Сигнал на выходе СФ с точностью до константы равен КФ
входного сигнала, сдвинутой вправо по оси времени на
величину t0
sвых (t0 ) BEsвх
2. Сигнал на выходе СФ при t=t0 с точностью до константы равен
энергии входного сигнала

10. АНАЛИЗ СОГЛАСОВАННОГО ФИЛЬТРА

СПМ шума на выходе СФ
N0 2 2
N0 2
B Sвх ( f )
Gn ( f ) Cсф ( f )
вых
2
2
КФ шума на выходе СФ
Kn
вых
( ) F
1
G
B 2 F
nвых ( f )
2 N0
1
B 2 s ( )
2
Sвх
(f)
2 N0
вх
3. КФ шума на выходе СФ с точностью до константы равна КФ
входного сигнала
4. Шум на выходе СФ коррелирован. КФ шума равна нулю
при
| | tc

11. АНАЛИЗ СОГЛАСОВАННОГО ФИЛЬТРА

Дисперсия шума на выходе СФ
2 N0
2 N0
Es
s (0) B
Dn Kn (0) B
вых
вых
2 вх
2 вх
sвых (t0 ) BEs
вх
Отношение сигнал/шум на выходе СФ при t=t0
2
2 Es
s
2
вых (t0 )
вх
qсф
Dn
N0
вых
5. Отношение сигнал/шум на выходе СФ зависит от энергии
полезного сигнала и интенсивности белого шума , т.е. зависит от
характеристик входного сигнала и входного шума

12. СФ ДЛЯ ПРЯМОУГОЛЬНОГО ВИДЕОИМПУЛЬСА

Информационный сигнал:
uc при 0 t tc ,
sвх (t )
0 при t 0 или t tc .
Примем:
t0 tc
Buc , 0 tc ,
hcф ( )
0, 0 и tc .
sвх (t )
uc
tc
t

13. СИНТЕЗ СФ

Спектральная плотность входного сигнала:
tc
Sвх ( f ) F{sвх (t )} uc exp( j 2 ft )dt
0
КЧХ СФ: t0 tc
uc
(1 exp( j 2 ftc ))
j 2 f
*
Hcф ( f ) BSвх
( f )exp( j 2 ft0 )
uc
B
(1 exp( j 2 ftc ))
j 2 f

14. АНАЛИЗ СФ

Энергия входного сигнала:
tc
Es
вх
uc2 dt uc2tc
0
Отношение сигнал/шум на выходе СФ:
2
2u
2
c tc
qсф
N0
Корреляционная функция входного сигнала:
2 | |
uc tc 1 t , | | tc ,
s ( )
c
вх
0, | | tc .

15.

АНАЛИЗ СФ
Сигнал на выходе СФ
B sвх (t tc ), 0 t 2tc ,
sвых (t )
0, t 0 или t 2tc ,
КФ шума на выходе СФ
2 N0
B 2 sвх ( ),| | tc ,
Kn ( )
вых
0, | | t .
c
Интервал корреляции выходного шума
( ) |
tc
tc
0
d 1 d
tc
K
(0)
2
0
n
0
вых
tc | K
nвых

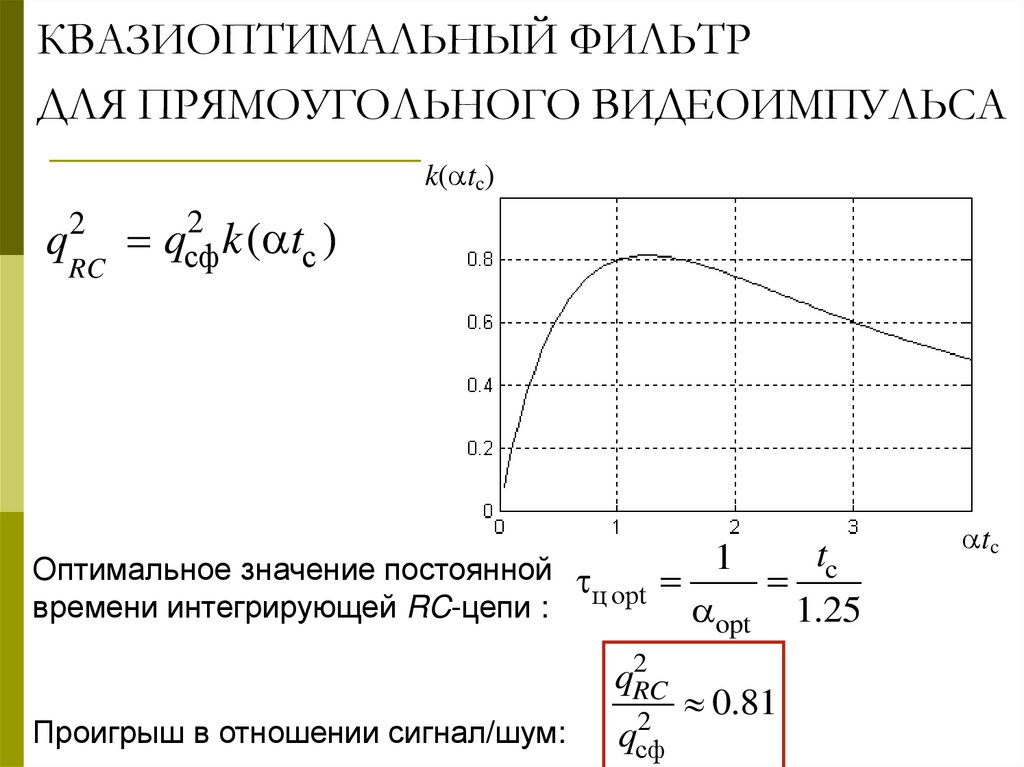
16. КВАЗИОПТИМАЛЬНЫЙ ФИЛЬТР ДЛЯ ПРЯМОУГОЛЬНОГО ВИДЕОИМПУЛЬСА

sвх(t)
ц 1 RC
sвых(t)
2
s
2
вых (t0 )
qRC
max
Dn
вых
Сигнал на выходе интегрирующей RC-цепи:
0, t 0.
sвых (t ) uc (1 exp( tc ))exp( (t tc )), t tc ,
uc (1 exp( t )), 0 t tc ,
Максимальное значение выходного
сигнала:
Дисперсия шума на выходе RC-цепи:
sвых (tc ) uc (1 exp( tc ))
N0
Dn
вых
2 2

17.

КВАЗИОПТИМАЛЬНЫЙ ФИЛЬТР
ДЛЯ ПРЯМОУГОЛЬНОГО ВИДЕОИМПУЛЬСА
Отношение сигнал/шум:
2
2
u
(1
exp(
t
))
c
q2 c
RC
N0
2 2
uc2tc (1 exp( tc ))2
N0
tc
2
2
2
2u
2
c tc
qсф
N0
2
q qсф
RC
2
2
(1 exp( tc ))2
tc
2
qсф
k ( tc )

18.

КВАЗИОПТИМАЛЬНЫЙ ФИЛЬТР
ДЛЯ ПРЯМОУГОЛЬНОГО ВИДЕОИМПУЛЬСА
k( tc)
2
k ( tc )
q2 qсф
RC
tc
1
Оптимальное значение постоянной
ц opt
времени интегрирующей RC-цепи :
opt 1.25
2
qRC
Проигрыш в отношении сигнал/шум:
2
qсф
0.81
tc

19.

ЭПЮРЫ СИГНАЛОВ И КФ ДЛЯ СФ И
ИНТЕГРИРУЮЩЕЙ RC-ЦЕПИ
sвх (t )
K nвх ( )
us
N0
2
tc
t
hсф ( )
h ( )
hRC (t )
Bus
tc
tc
tc
Kn
вых
( )
uc (1 exp( tc ))
BEsвх
sвых (t )
B2
tc
2tc
t
tc
N0
Esвх
2
2tc
N0
2 2
tc
tc
tc

20. СФ ДЛЯ ПРЯМОУГОЛЬНОГО РАДИОИМПУЛЬСА

Информационный сигнал:
uc sin(2 f0t ) при 0 t tc ,
sвх (t )
0 при t 0 и t tc .
Примем:
t0 tc
Buc sin(2 f0t ), 0 t tc ,
hсф (t )
0, t 0 и t tc ,
где
2n 1
f0tc
2

21.

СТРУКТУРНАЯ СХЕМА СФ
hсф(t)
hсф(t)
Buc
sвх(t)
sвых(t)
%
sвх(t)
Buc
sвых(t)

22.

АНАЛИЗ СФ
Энергия входного
сигнала:
tc
2
u
2
2
c tc
Es uc (sin 2 f0t ) dt
вх
2
0
Отношение сигнал/шум
на выходе СФ:
2
u
2 c tc
2
qсф
N0 2
Корреляционная функция входного сигнала:
uc2tc | |
1
cos 2 f0 , | | tc ,
tc
s ( ) 2
вх
0, | | tc .

23.

СИГНАЛ И КФ НА ВЫХОДЕ СФ
uc2tc | t tc |
B
1
cos 2 f0t при 0 t 2tc ,
tc
sвых (t ) 2
0 при t 0 и t 2tc ;
2 N0 uc2tc | |
B
1
cos 2 f0 при | | tc ,
2 2
tc
Kn ( )
вых
0 при | | tc .
Интервал корреляции по огибающей КФ:
tc
tc
0 1 d
tc
2
0

24. КВАЗИОПТИМАЛЬНЫЙ ФИЛЬТР ДЛЯ ПРЯМОУГОЛЬНОГО РАДИООИМПУЛЬСА

iвх
Резонансная частота:
R
C
1
f0
2 LC
uвых
L
uвых =iвхRрез =iвхR
Постоянная времени контура:
1
2Q
k k 2 RC
2 f0
k
h( ) 2R k e
Импульсная характеристика:
КЧХ:
H( f )
R
1 j 2 ( f f0 ) k 1
cos(2 f0 )

25.

КВАЗИОПТИМАЛЬНЫЙ ФИЛЬТР
ДЛЯ ПРЯМОУГОЛЬНОГО РАДИООИМПУЛЬСА
Максимальное значение выходного сигнала:
sвых (tc ) uc R(1 exp( k tc ))
Дисперсия шума на выходе RLC-контура:
N0 2
Dn
R k
вых
2
Отношение сигнал/шум:
2
2
u
(1
exp(
t
))
2
2
2
2
c
k c
q
qcф
(1 exp( k tc ))2 qcф
k ( k tc )
LC
N0
k tc
k
2

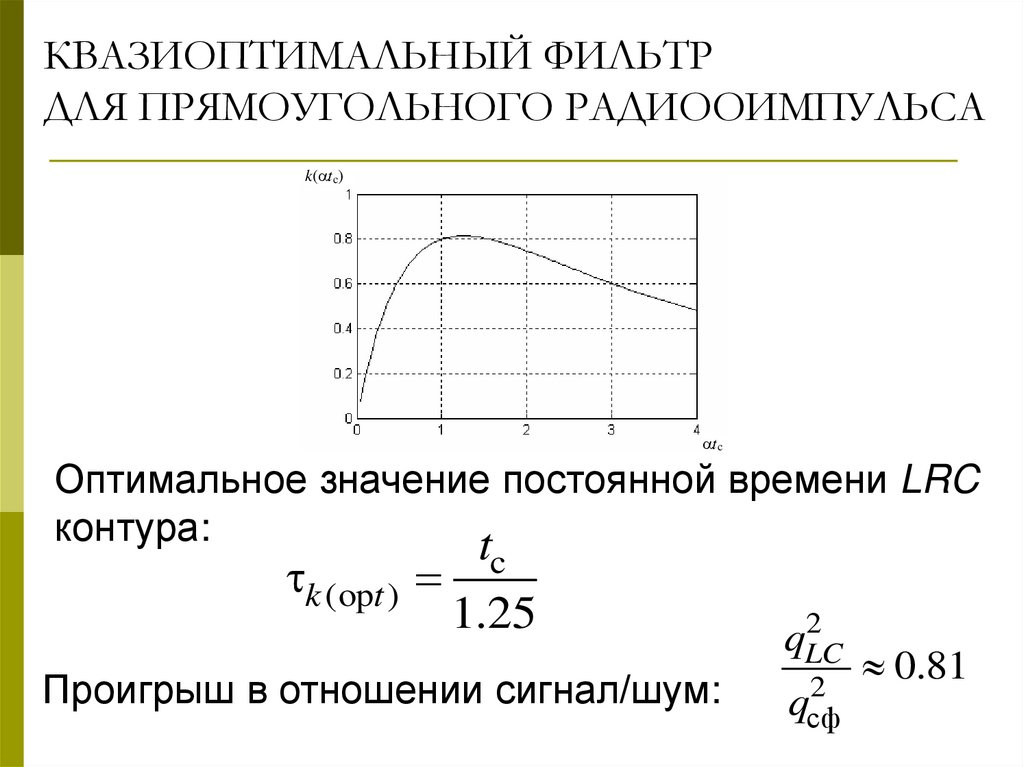
26.

КВАЗИОПТИМАЛЬНЫЙ ФИЛЬТР
ДЛЯ ПРЯМОУГОЛЬНОГО РАДИООИМПУЛЬСА
k( t c)
t c
Оптимальное значение постоянной времени LRC
контура:
t
k (opt )
c
1.25
Проигрыш в отношении сигнал/шум:
2
qLC
2
qсф
0.81

27. СФ КАК КОРРЕЛЯТОР

hсф ( ) Bsвх (t0 )
sвых ( ) B s ( t0 )
вх
z(t ) sвх (t )
t
sвых (t ) hсф ( )z (t )d
0
t
B sвх (t0 )z (t ) d B s z (t t0 )
вх
0

28. СХЕМЫ КОРРЕЛЯТОРА И СФ

СФ

29. СФ КАК КОРРЕЛЯТОР

1.Отношение сигнал/шум на выходе СФ при t=t0 равно
отношению сигнал/шум на выходе коррелятора с опорным
сигналом, равным sвх (t )
2.Сигналы на выходе СФ и коррелятора не совпадают по
форме