Влияние внешних сил на колебательные процессы

1.

ЛЕКЦИЯ 2 (часть 1)
Сегодня: пятница, 13 июня 2025 г.
Тема 3.
ВЛИЯНИЕ ВНЕШНИХ СИЛ НА КОЛЕБАТЕЛЬНЫЕ ПРОЦЕССЫ
3.1. Свободные затухающие механические
колебания
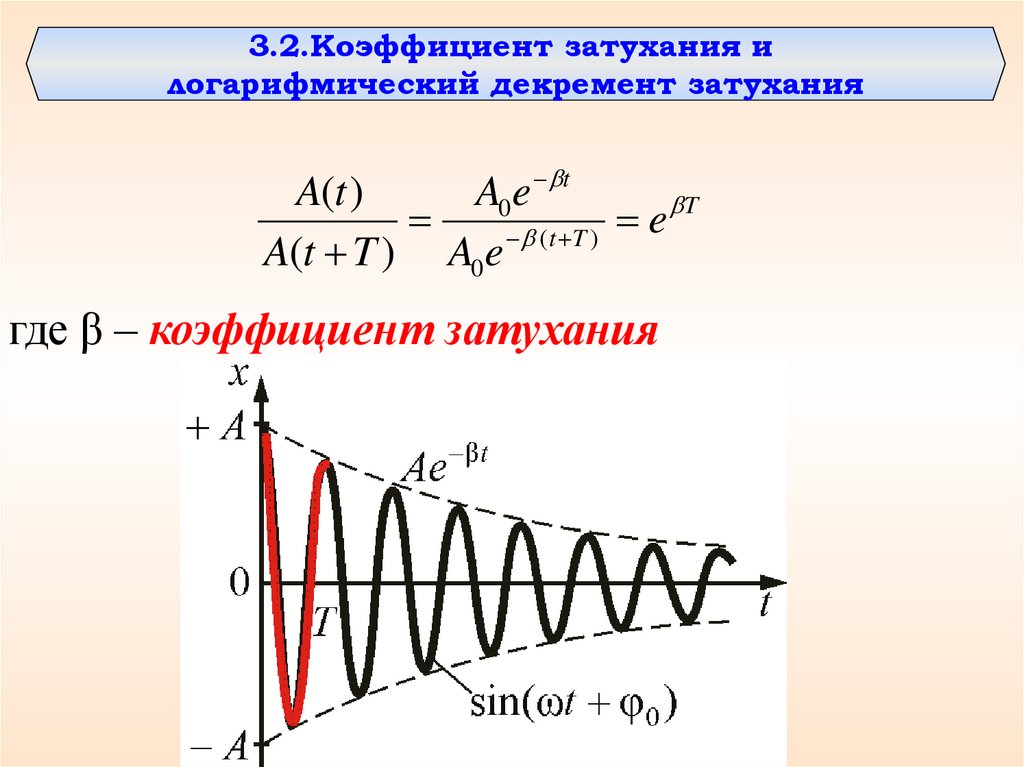
3.2. Коэффициент затухания и
логарифмический декремент затухания
3.3. Вынужденные механические колебания

2.

3.1. Свободные затухающие механические колебания
Все реальные колебания являются затухающими.
Энергия механических колебаний постепенно
расходуется на работу против сил трения и
амплитуда колебаний уменьшается.
Сила трения (или сопротивления)
Fтр r
где r – коэффициент сопротивления,
– скорость движения

3.

Второй закон Ньютона для затухающих
прямолинейных колебаний вдоль оси x
max kx r x
где kx – возвращающая сила, r x– сила трения.
d 2 x r dx k
x 0
2
dt
m dt m
Введем обозначения
r
;
2m
k
2
0
m
2
d x
dx
2
2
0x 0
2
dt
dt
Решение уравнения (3.1.1) имеет вид (при 0 )
(3.1.1)

4.

Решение уравнения (3.1.1) имеет вид
x A0e
t
(3.1.2)
cos( t )
Найдем частоту колебаний ω. (ω ω0 )
β ω0
2 2
0
k
0
m
;
2
k r
.
m 2m
r
2m ;
условный период
T
2
2
2
0
2
,

5.

3.2.Коэффициент затухания и
логарифмический декремент затухания
t
A0e
A(t )
T
e
A(t T ) A0e (t T )
где β – коэффициент затухания

6.

Логарифмическим декрементом затухания
называется натуральный логарифм отношения
амплитуд, следующих друг за другом через
период Т.
A(t )
ln
ln e T T ;
A(t T )
T
A0
1
e e , откуда 1;
A
1
.
Следовательно, коэффициент затухания β – есть
физическая величина, обратная времени, в течение
которого амплитуда уменьшается в е раз,
τ – время релаксации.

7.

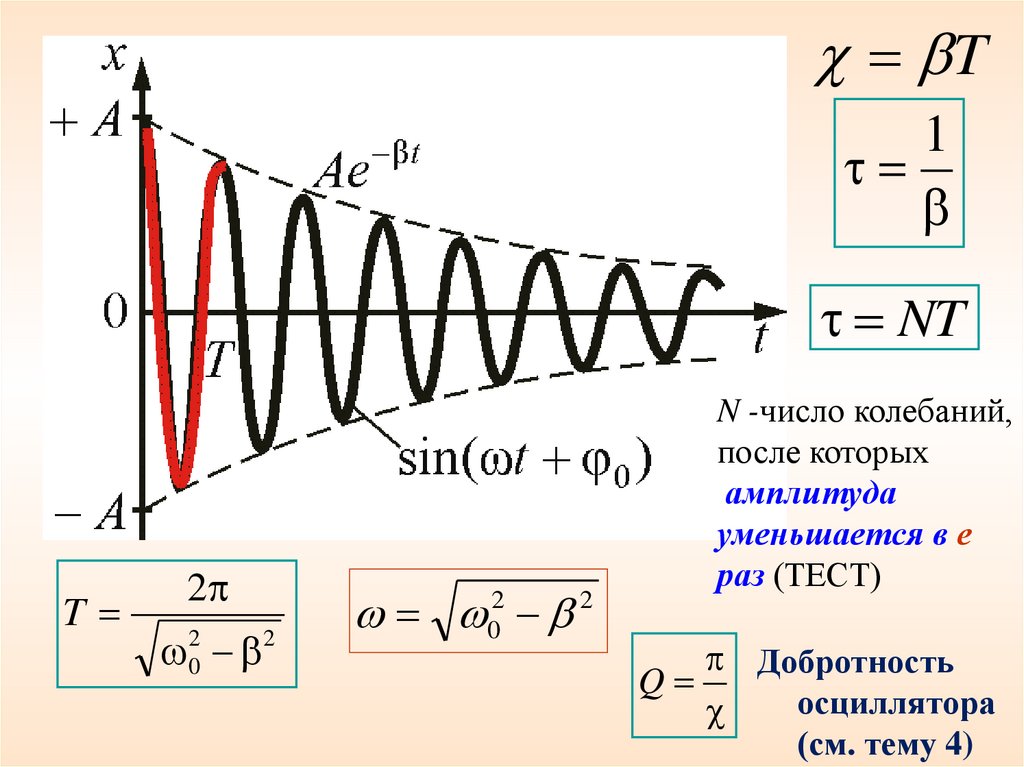
T
1
NT
T
2
2
0
2
2
0
2
N -число колебаний,
после которых
амплитуда
уменьшается в е
раз (ТЕСТ)
Добротность
Q
осциллятора
(см. тему 4)

8.

3.3. Вынужденные механические колебания
Рассмотрим систему, на которую кроме упругой
силы (– kx) и сил сопротивления (– rυ) действует
добавочная периодическая сила Fx– вынуждающая
Fx F0 cos t
сила:
max kx r x Fx
– основное уравнение колебательного процесса,
при вынужденных колебаниях
2
d x
dx
2
2 0 x f 0 cos t
2
dt
dt
r
2m
k
02
m
F0
f0
m
(3.3.1)

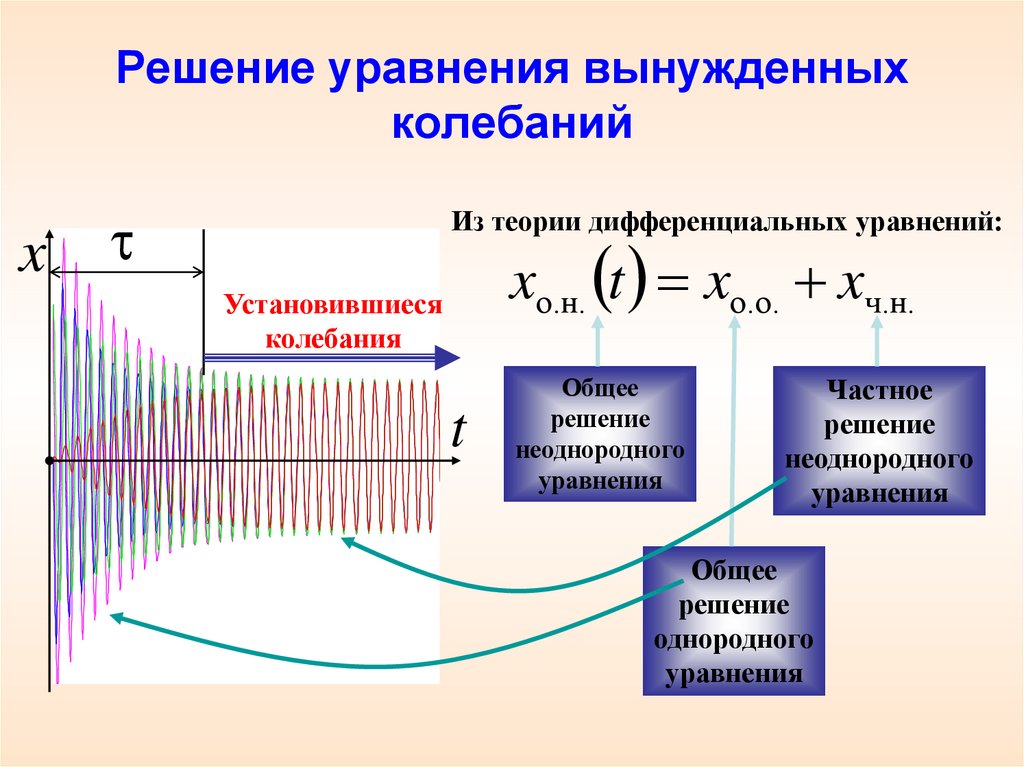
9. Решение уравнения вынужденных колебаний

x
Из теории дифференциальных уравнений:
xо.н. t xо.о. xч.н.
Установившиеся
колебания
t
Общее
решение
неоднородного
уравнения
Частное
решение
неоднородного
уравнения
Общее
решение
однородного
уравнения

10.

Установившиеся колебания представляют собой
гармонические колебания. Подберем начало отсчета
времени таким образом, чтобы начальная фаза была
равна нулю, и будем искать решение – функцию вида
x A cos t
(3.3.2)
Наша задача найти амплитуду А и разность фаз φ
между смещением вынужденных колебаний и
вынуждающей силой.
Введем обозначения:
A 2 – амплитуда ускорения;
2 A – амплитуда скорости;
A 02
– амплитуда смещения;
f 0 – амплитуда вынуждающей силы

11. Векторная диаграмма вынужденных колебаний

x t A cos t
2 A
f 0 x 2 x 2 x f cos t
0
0
x
t
A
sin
t
A 02
A
2
x t A cos t
2
2
2 2
2
2 A A 0 A f0
f0
2
A
tg 2
2
2
2
2 2
0
0 4
2
(3.3.3)
(3.3.4)

12.

A
f0
( 02 2 ) 2 4 2 2
Проанализируем выражение (3.3.3).
1) 0 (частота вынуждающей силы равна нулю)
x f 0 / m 02
–
статическая
амплитуда,
колебания
не
совершаются.
2) β 0 (затухания нет). С увеличением ω (но при
ω ω0), амплитуда растет и при ω ω0 , амплитуда
резко возрастает ( А ). Это явление называется
– резонанс. При дальнейшем увеличении ( ω ω0 )
амплитуда опять уменьшается.
3) 0 рез 02 2 2
– резонансная частота

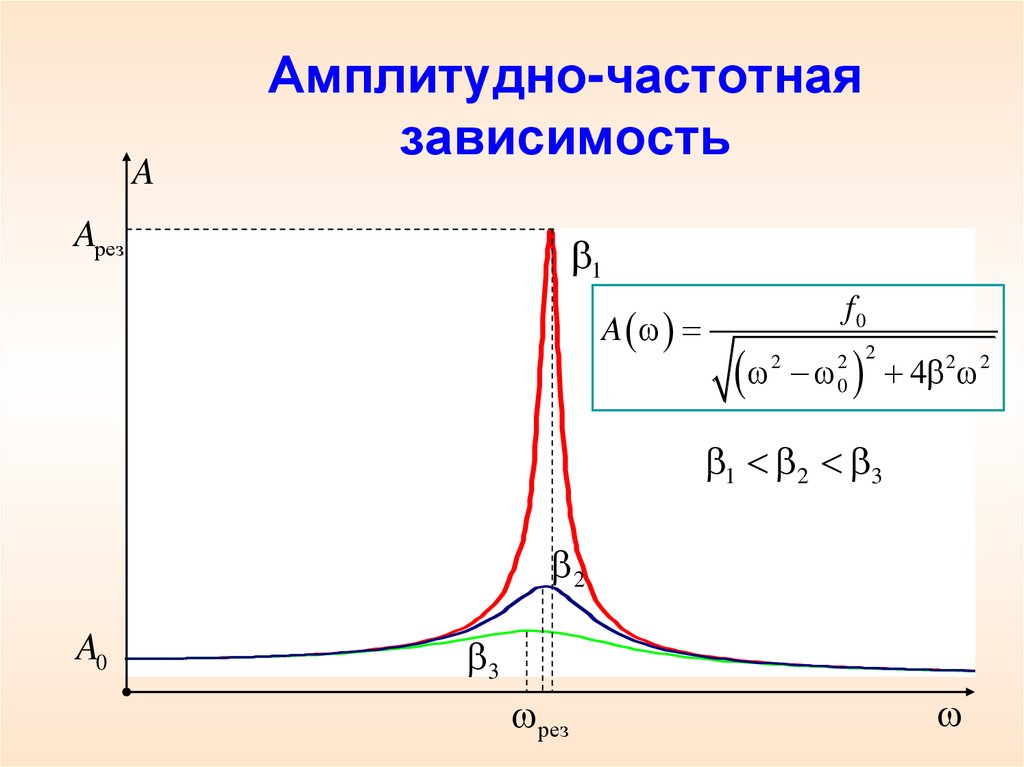
13. Амплитудно-частотная зависимость

A
Амплитудно-частотная
зависимость
Aрез
1
A
f0
2 2
4
2
2 2
0
1 2 3
2
A0
3
рез

14.

рез 2 – резонансная частота.
2
0
2
Явление возрастания амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы к собственной частоте
колебаний системы называется резонансом.
Для консервативной системы, т.е. β 0, рез 0
для диссипативной рез несколько меньше
собственной круговой частоты ω 0.
С увеличением коэффициента затухания β явление
резонанса проявляется все слабее и исчезает при
0
2