Призма Види призм

1. Тема: Пряма і правильна призми. Площі бічної і повної поверхні призми.

Виконала викладач вищої категорії
м.Нікополь “НЦПО”
Ганжа А.Г.

2.

ПРИЗМА
Призмою називається многогранник, у
якого дві грані — рівні n-кутники,
розташовані в паралельних площинах,
а решта n граней — паралелограми.

3.

Властивості призми
• Основи призми є рівними многокутниками.
• Бічні грані призми є паралелограмами.
• Ребра призми – це сторони бічних граней і
основ
• Бічні ребра призми рівні.
• Висота призми — відстань між площинами її
основ.
• Діагональний переріз
будь – якої призми –
паралелограм.

4.

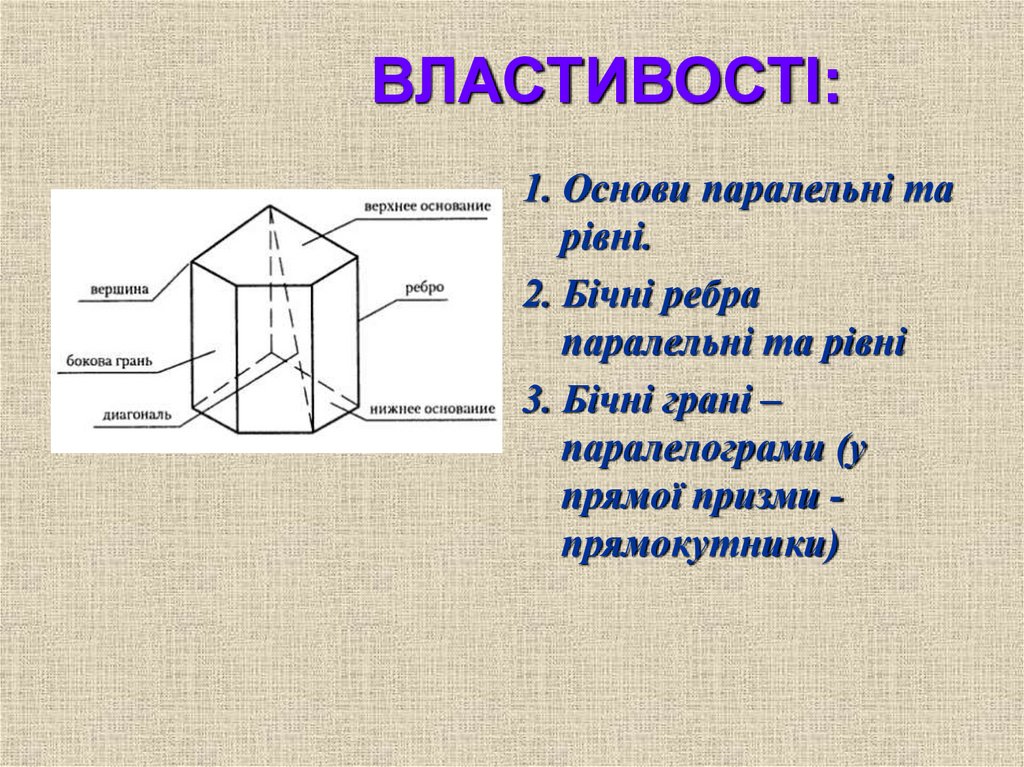
ВЛАСТИВОСТІ:
1. Основи паралельні та
рівні.
2. Бічні ребра
паралельні та рівні
3. Бічні грані –
паралелограми (у
прямої призми прямокутники)

5.

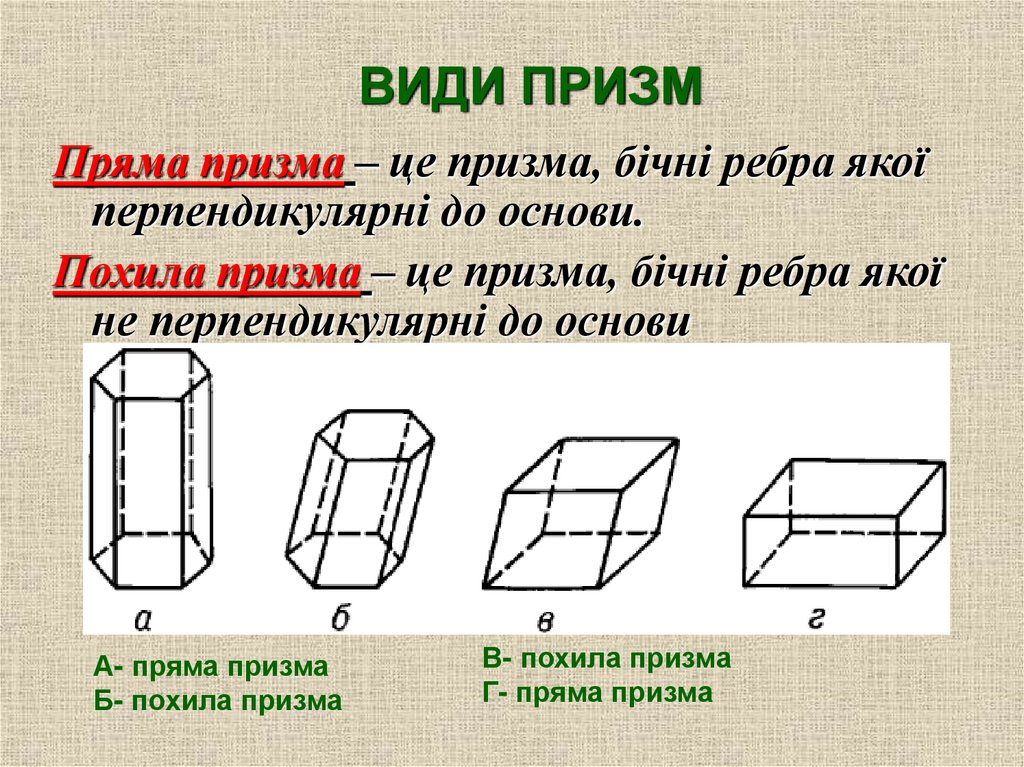
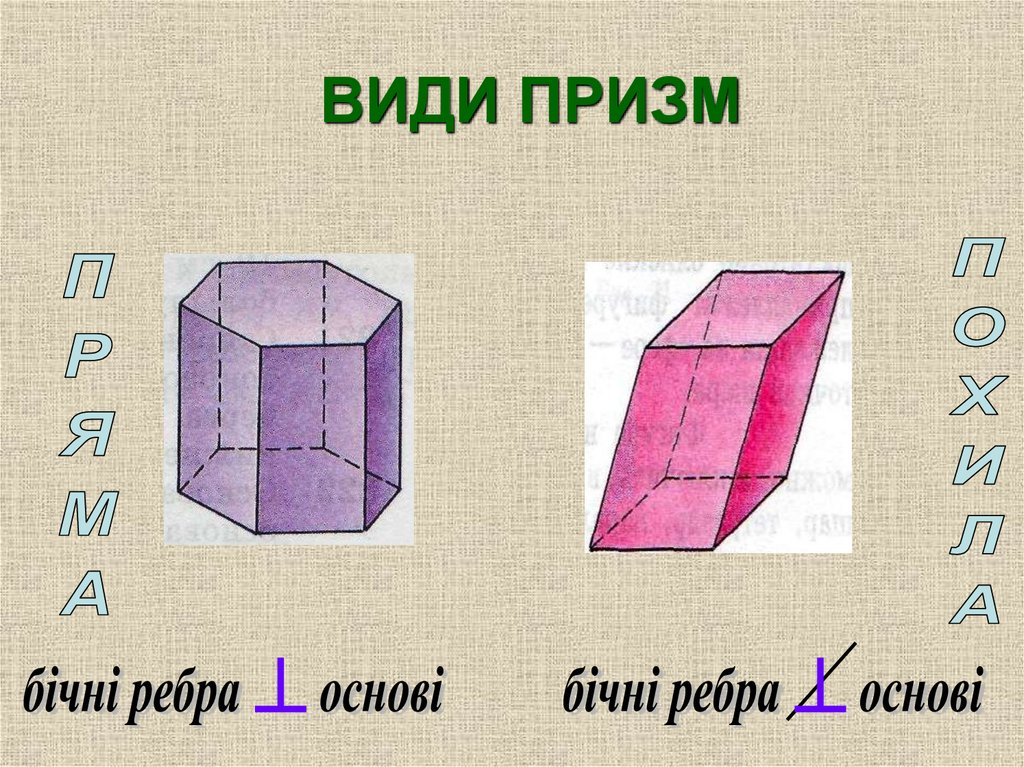
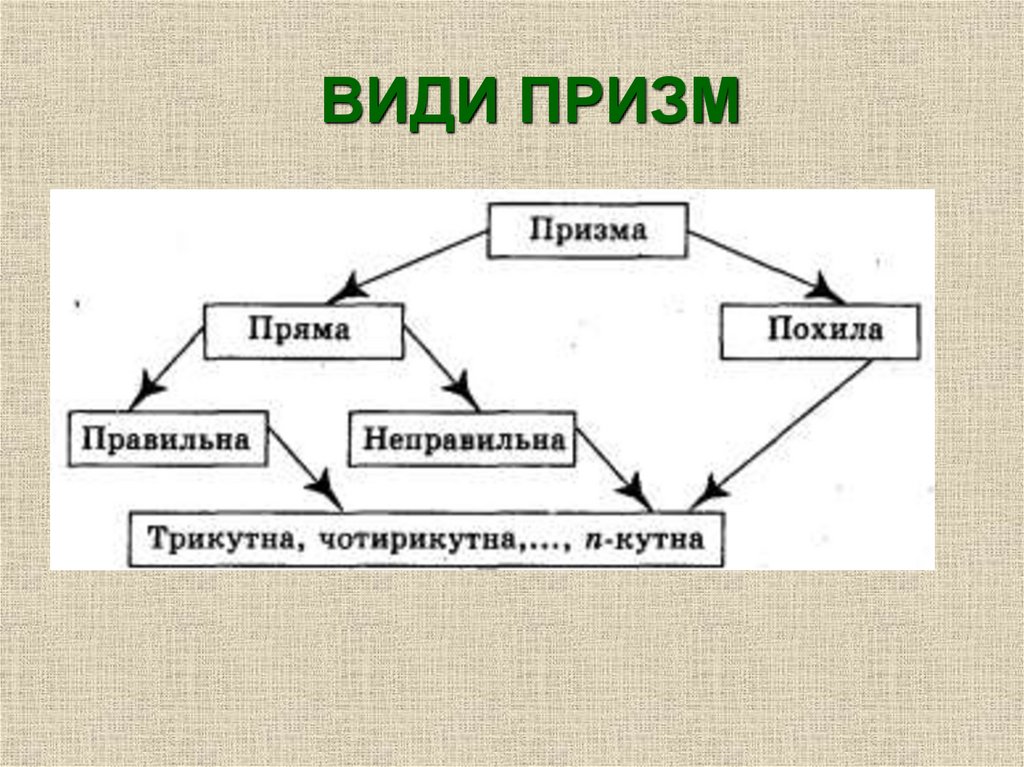
ВИДИ ПРИЗМ
Пряма призма – це призма, бічні ребра якої
перпендикулярні до основи.
Похила призма – це призма, бічні ребра якої
не перпендикулярні до основи
А- пряма призма
Б- похила призма
В- похила призма
Г- пряма призма

6.

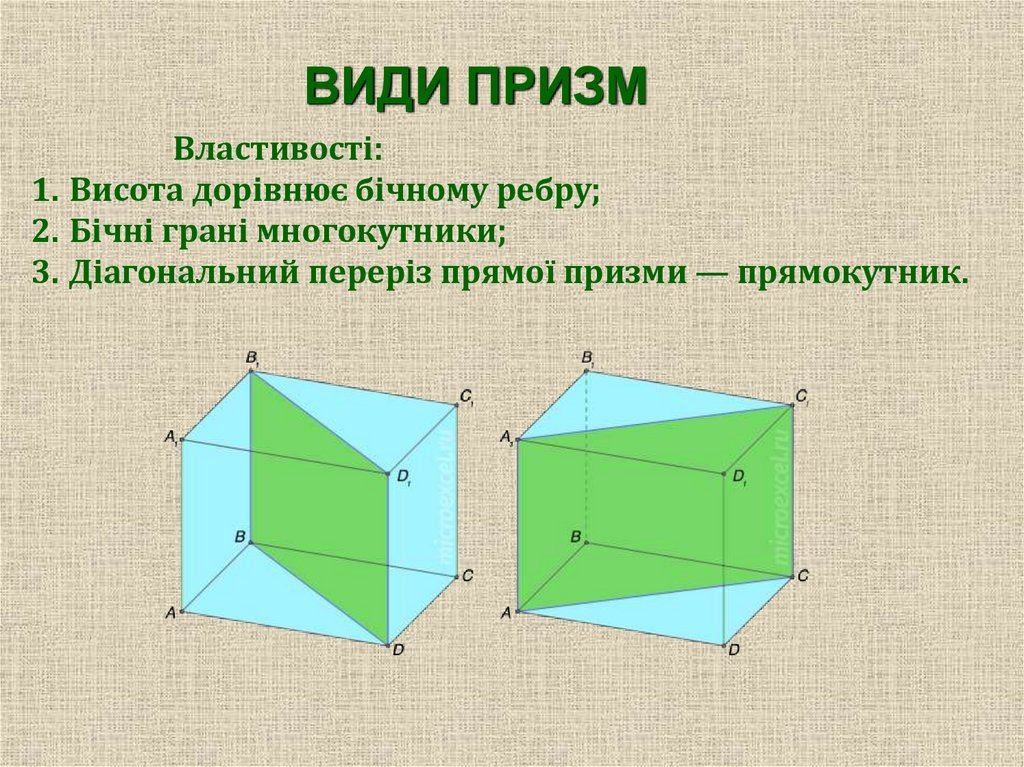
ВИДИ ПРИЗМ
Властивості:
1. Висота дорівнює бічному ребру;
2. Бічні грані многокутники;
3. Діагональний переріз прямої призми — прямокутник.

7.

ВИДИ ПРИЗМ

8.

ВИДИ ПРИЗМ
• Правильна призма – це пряма
призма, в основі якої лежитть
правильний багатокутник
Бічні ребра перпендикулярні до основи;
Усі бічні грані прямокутники;
Бічне ребро є висотою призми;

9.

ВИДИ ПРИЗМ

10.

144
Розв’язування задач
В основі прямої призми лежить квадрат.
Діагональ призми 13 см, висота 5 см.
Знайти довжину діагоналі бічної грані.
Дано:
АВСDА1В1С1D1 – пряма призма
АВСD – квадрат
В1D – діагональ призми; В1D = 13см
АА1 – висота; АА1 = 5 см
Знайти: DС1 – ?
Розв’язання: З трикутника ВВ1D
В основі лежить квадрат.
(90о) за теоремою
d = a √2;а = ВС = d /√2 =
Піфагора В1D2 = В1В2+ ВD2
= 12 /√2 = 6∙ √2 .
ВD2 = В1D2 – ВВ; ВD2 = 132 – 52 =
С1D2 = DС2 + СС2;
= = 169 – 25 = 144; ВD = d = 12 (см)
С1D2 = 72 +25 = 97
С1D = √97(см)

11.

БІЧНА ТА ПОВНА
ПОВЕРХНЯ ПРИЗМИ
Sбіч. = P осн. ∙H
– площа бічної
поверхні
Sп. = Sбіч. + 2Sосн.
– площа повної поверхні

12.

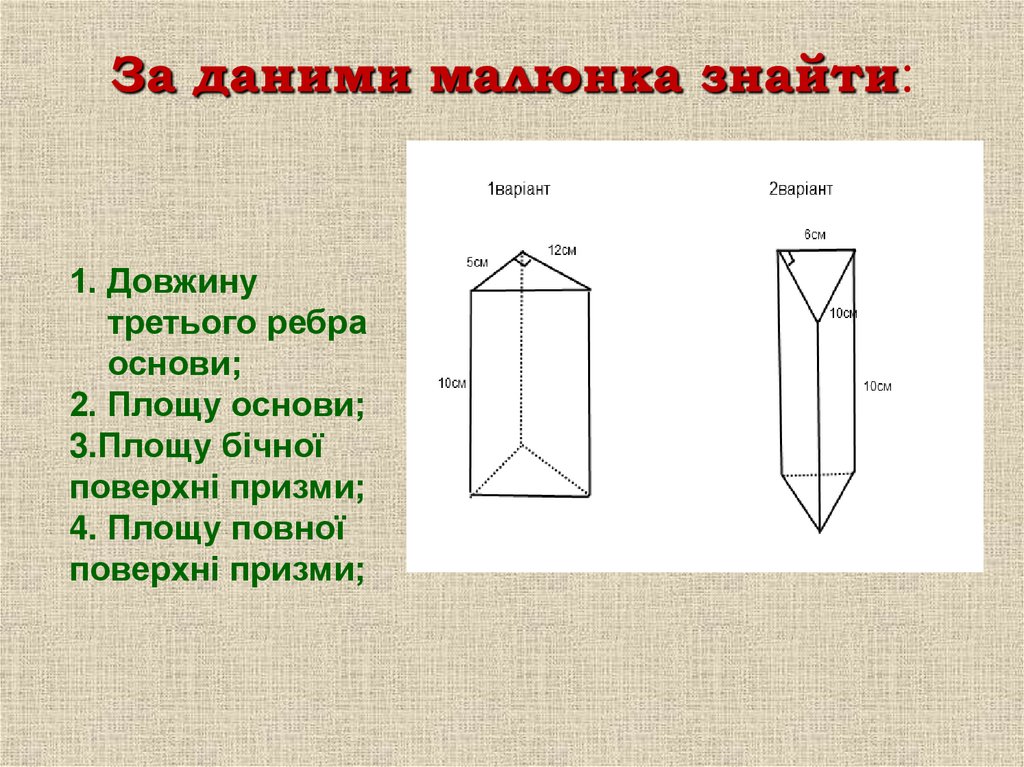
1. Довжину
третього ребра
основи;
2. Площу основи;
3.Площу бічної
поверхні призми;
4. Площу повної
поверхні призми;

13.

Основа прямокутної призми прямокутний
трикутник з катетом 6 см і гіпотенузою 10 см.
Висота дорівнює 15 см. Знайдіть площу
поверхні призми.
Дано:АВ С A1B1С1 – призма
А1B1 = 10 см; А1С1 = 6см; АА1 = H = 15 см
Знайти: Sпов. – ?
Sпов. = Sбіч +2 Sосн; Sбіч = Росн ∙ H
Росн = А1С1 + B1C1 + A1B1; Sосн = А1С1 ∙ B1C1.
90о)
За теоремою Піфагора з тр. А1B1С1(кут С =
(B1C1)2 = (А1B1)2 - (А1С1)2 = 102 - 62 = 100 – 36 =
64;
B1C1 = 8(см).
Росн = 6 + 8 + 10 = 24(см); Sбіч = 24∙15 = 360(см2)
Sосн = 6∙8 = 24(см2); 2Sосн = 2∙24 = 48(см2).
Sпов. = 360 +48 = 408(см2).

14.

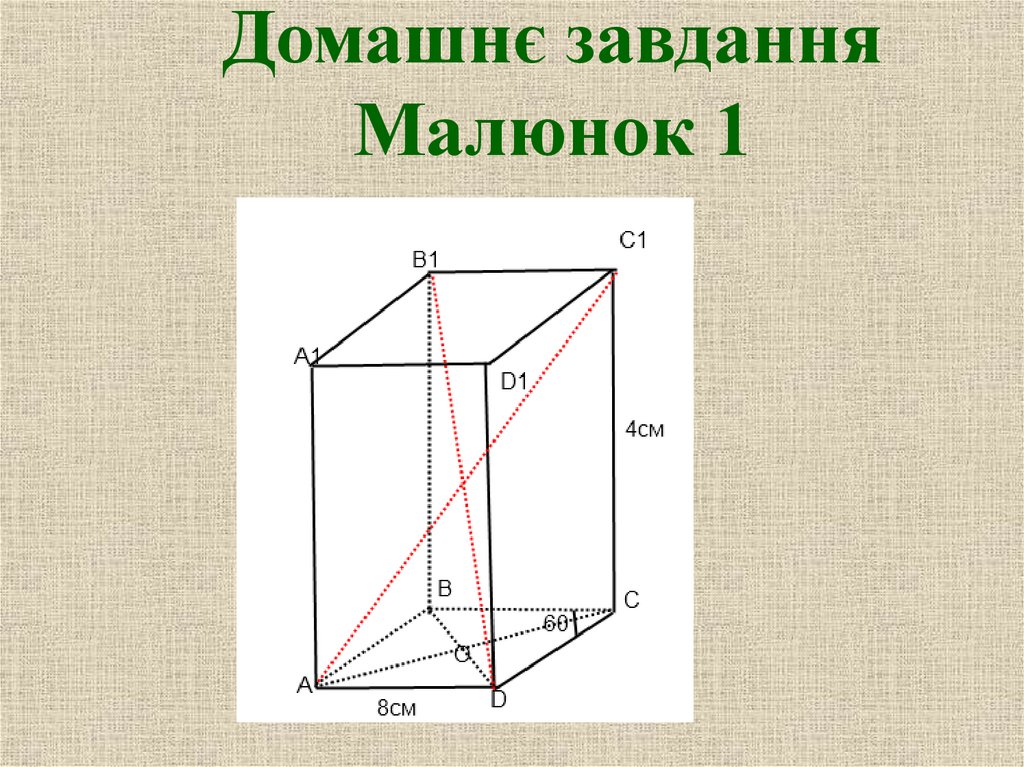
Домашнє завдання
Розв'язати
задачу
• В основі прямої призми
лежить ромб з гострим
кутом 60° і стороною 8 см.
Знайти діагональ призми,
якщо її бічне ребро дорівнює 4
см.

15.

Домашнє завдання
Малюнок 1

16.

ПРИЗМИ У НАШОМУ ЖИТТІ

17.

ПРИЗМИ В АРХІТЕКТУРІ

18.

Рефлексія діяльності
Продовжить фразу
- Мені було цікаво...
- Ми сьогодні
розібралися...
-Я сьогодні зрозумів,
що...
- Мені було важко...
- Завтра я хочу на уроці