Похожие презентации:
Призма
1. КЛАСНА РОБОТА 28.09.21
ПРИЗМА2.
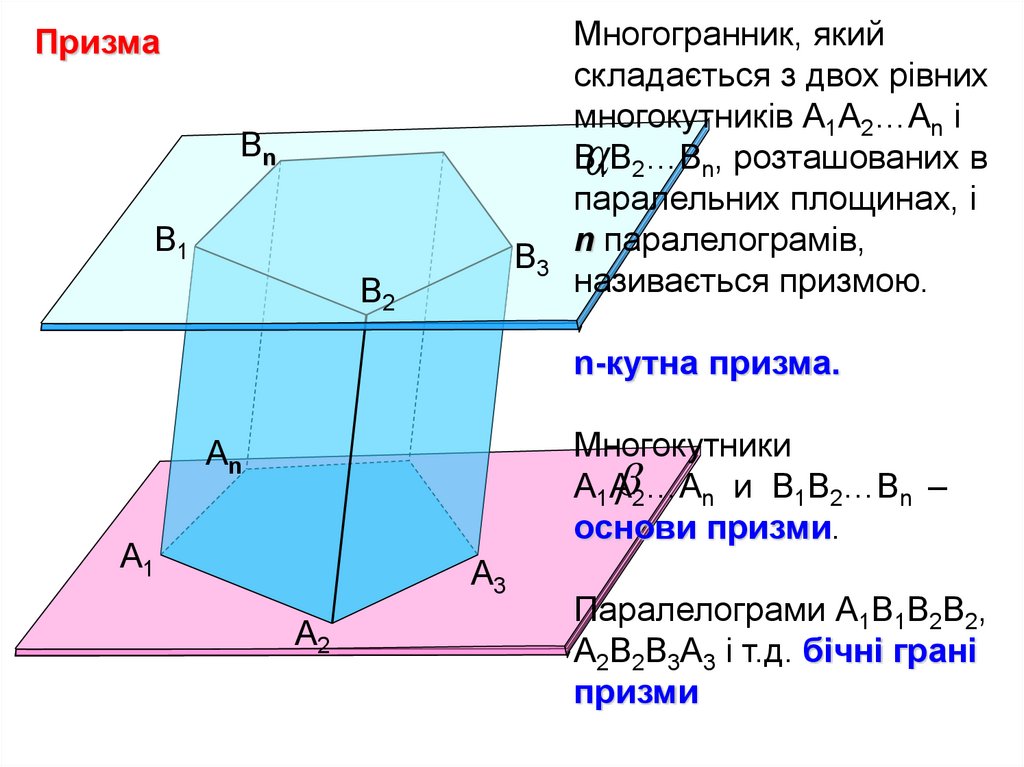
ПризмаМногогранник, який
складається з двох рівних
многокутників А1А2…Аn і
В1В2…Вn, розташованих в
паралельних площинах, і
n паралелограмів,
називається призмою.
Bn
B1
B3
B2
n-кутна призма.
Многокутники
2…Аn и В1В2…Вn –
А1А
основи призми.
Аn
А1
А3
А2
Паралелограми А1В1В2В2,
А2В2В3А3 і т.д. бічні грані
призми
3.
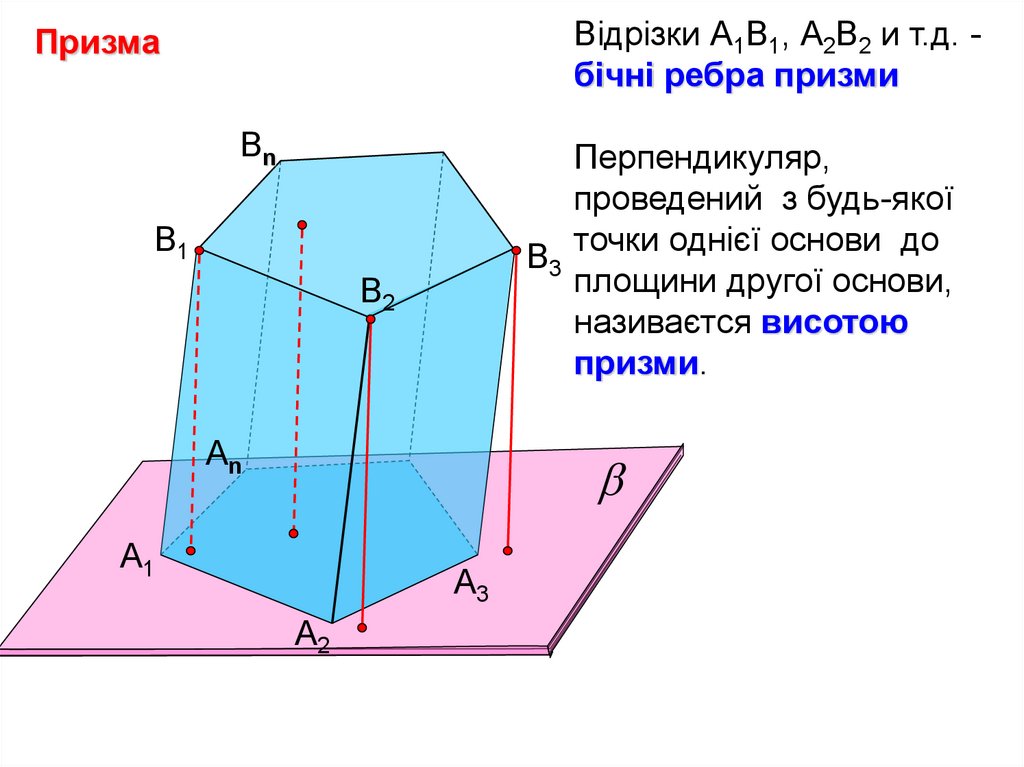
Відрізки А1В1, А2В2 и т.д. бічні ребра призмиПризма
Bn
Перпендикуляр,
проведений з будь-якої
B3 точки однієї основи до
площини другої основи,
називаєтся висотою
призми.
B1
B2
Аn
А1
А3
А2
4.
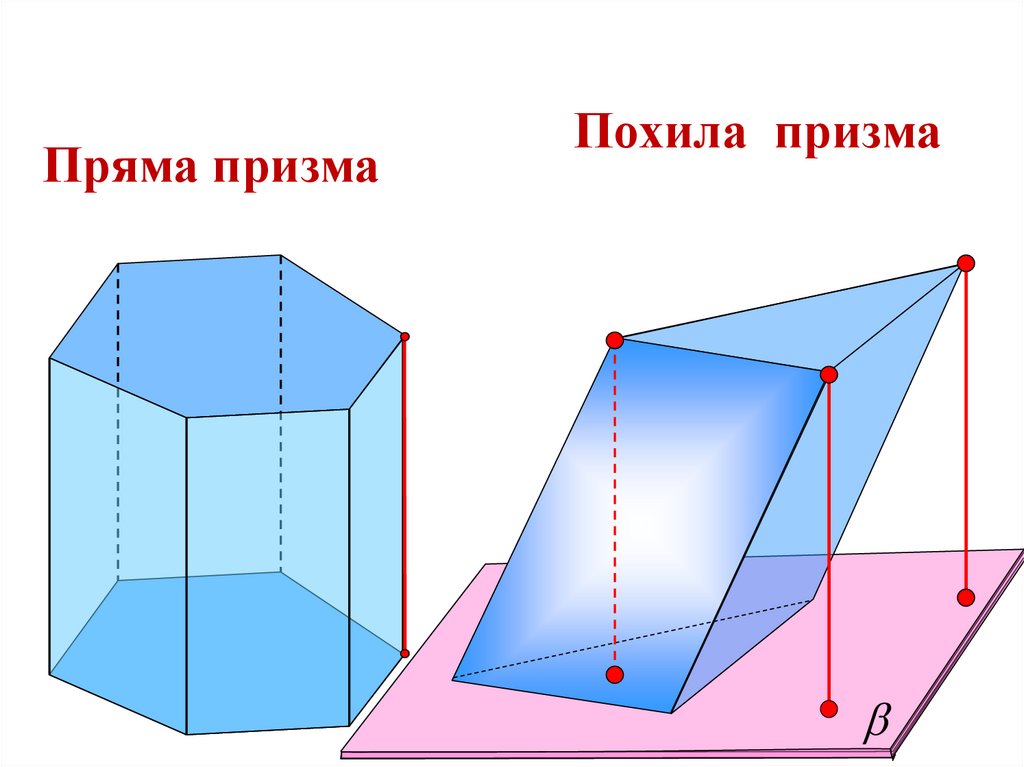
Пряма призмаПохила призма
5.
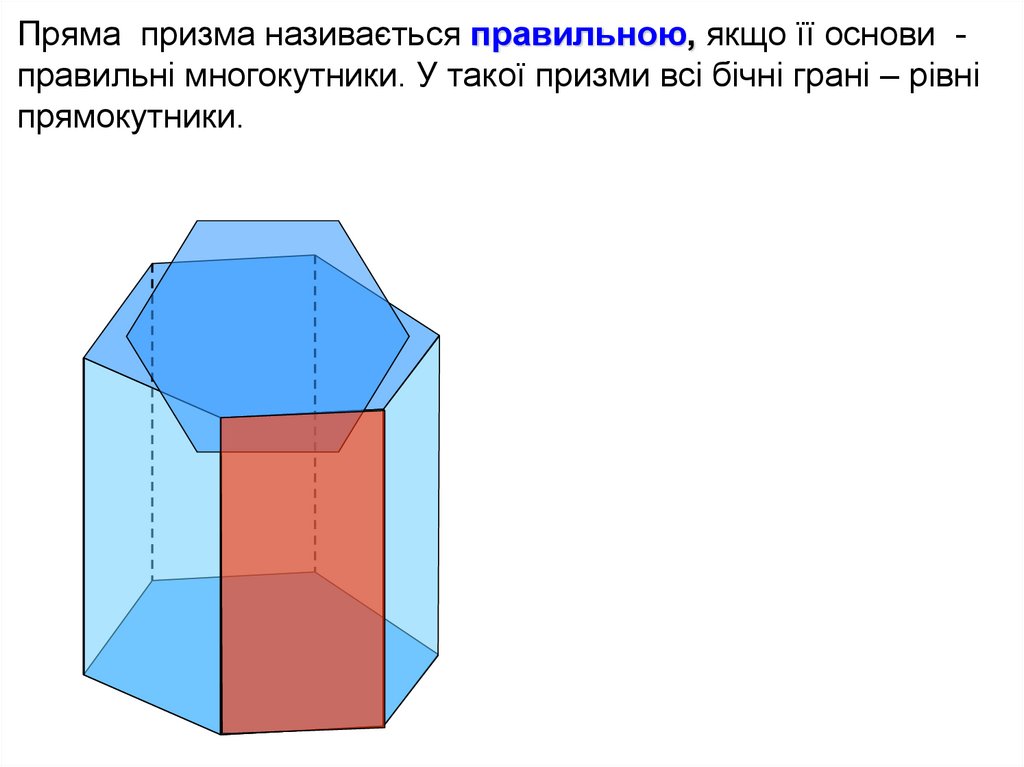
Пряма призма називається правильною, якщо її основи правильні многокутники. У такої призми всі бічні грані – рівніпрямокутники.
6.
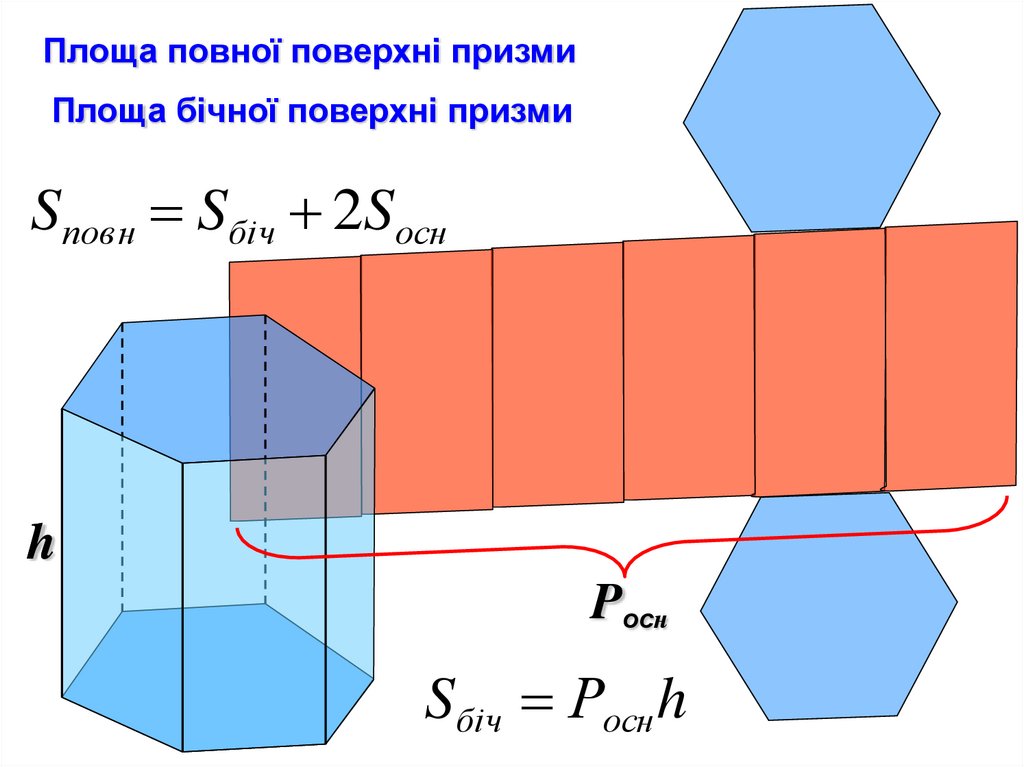
Площа повної поверхні призмиПлоща бічної поверхні призми
Sповн Sбіч 2Sосн
h
Pocн
Sбіч Росн h
7.
Прямокутний паралелепіпед8.
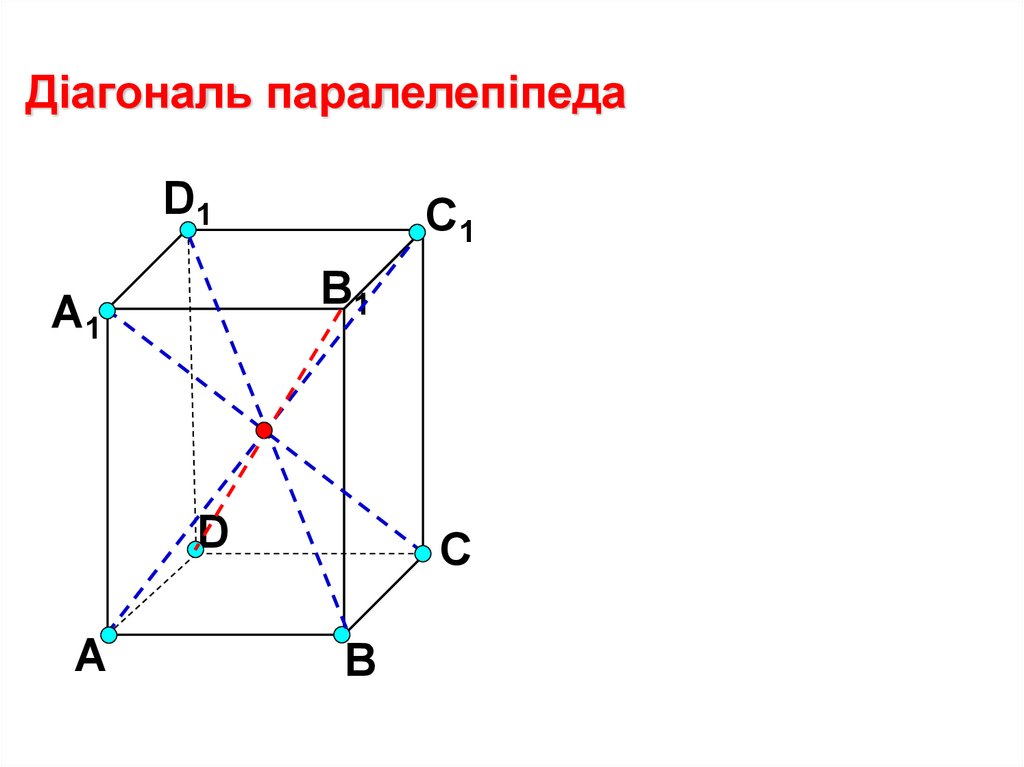
Діагональ паралелепіпедаD1
С1
B1
А1
D
А
С
В
9.
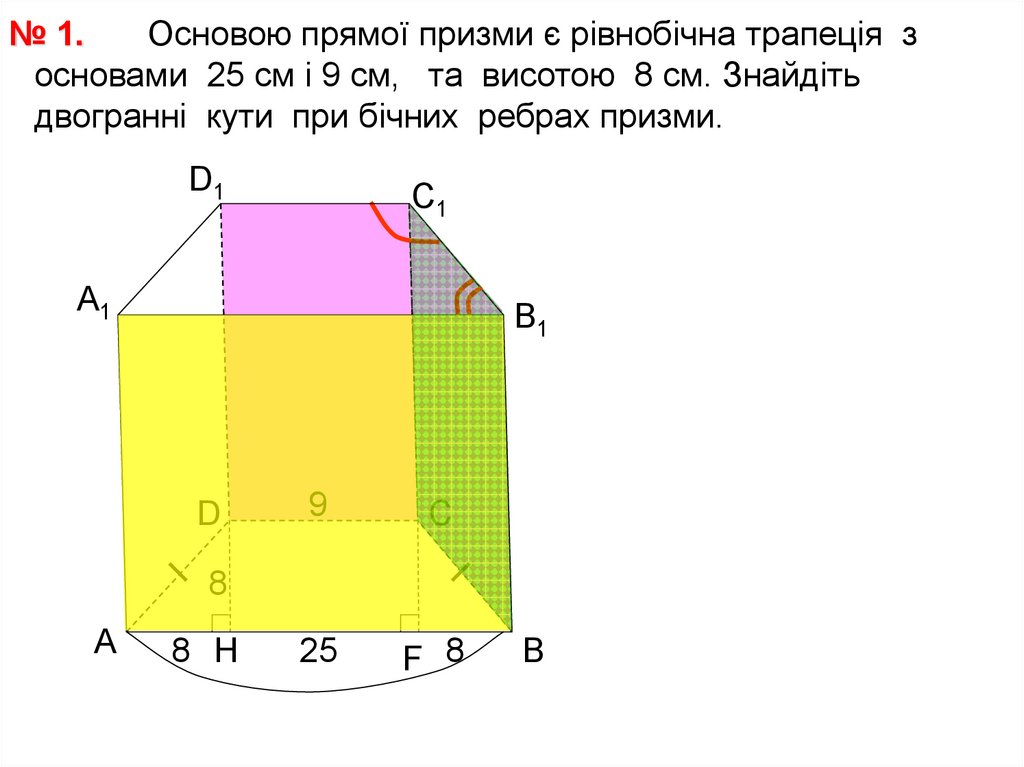
№ 1.Основою прямої призми є рівнобічна трапеція з
основами 25 см і 9 см, та висотою 8 см. Знайдіть
двогранні кути при бічних ребрах призми.
D1
С1
А1
В1
D
9
С
25
F 8
8
А
8 H
В
10.
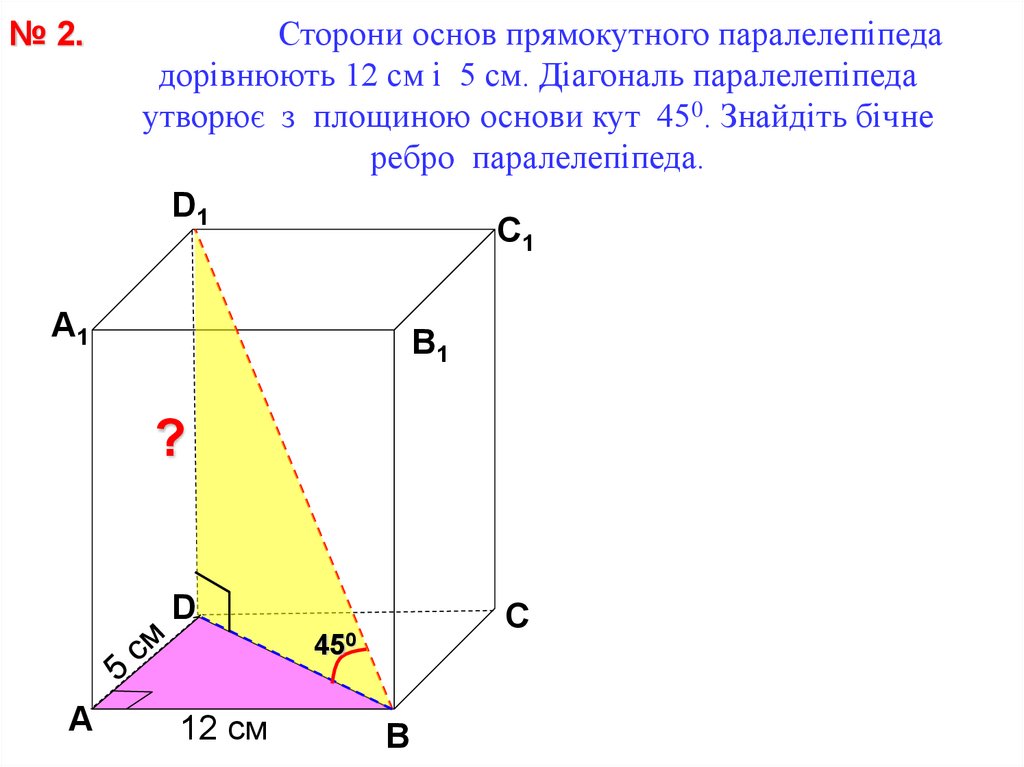
№ 2.Сторони основ прямокутного паралелепіпеда
дорівнюють 12 см і 5 см. Діагональ паралелепіпеда
утворює з площиною основи кут 450. Знайдіть бічне
ребро паралелепіпеда.
D1
С1
А1
В1
?
D
С
450
А
12 см
В
11.
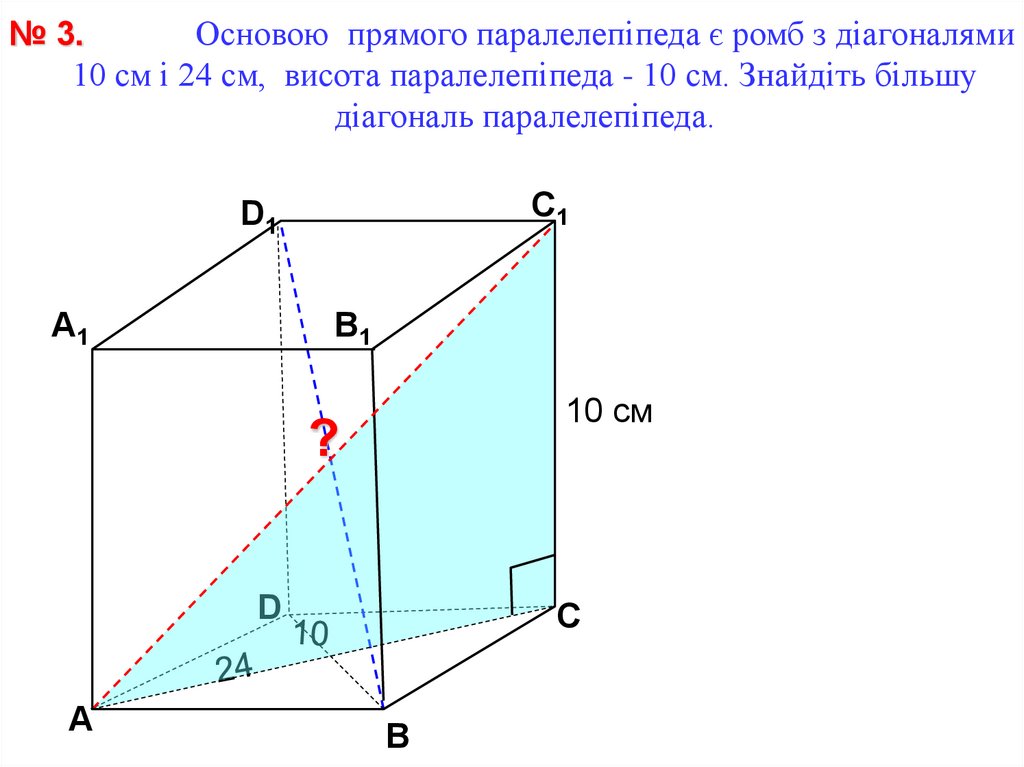
Основою прямого паралелепіпеда є ромб з діагоналями№ 3.
10 см і 24 см, висота паралелепіпеда - 10 см. Знайдіть більшу
діагональ паралелепіпеда.
С1
D1
А1
В1
10 см
?
D
А
С
В
12.
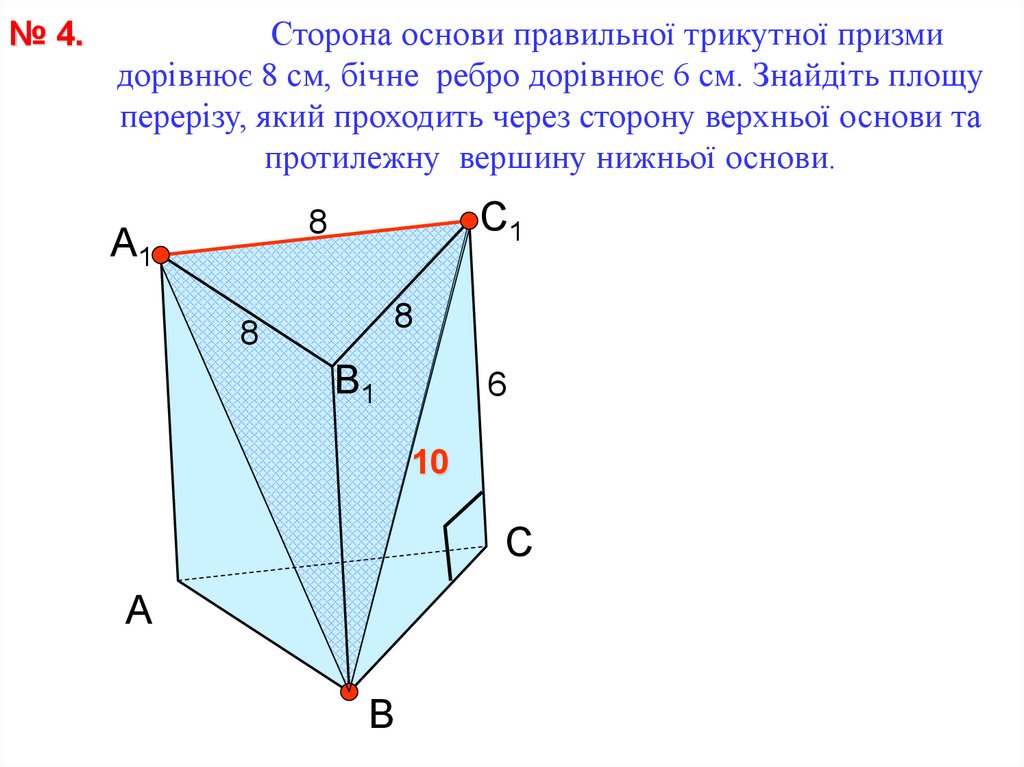
№ 4.Сторона основи правильної трикутної призми
дорівнює 8 см, бічне ребро дорівнює 6 см. Знайдіть площу
перерізу, який проходить через сторону верхньої основи та
протилежну вершину нижньої основи.
С1
8
А1
8
8
В1
6
10
С
А
В
13.
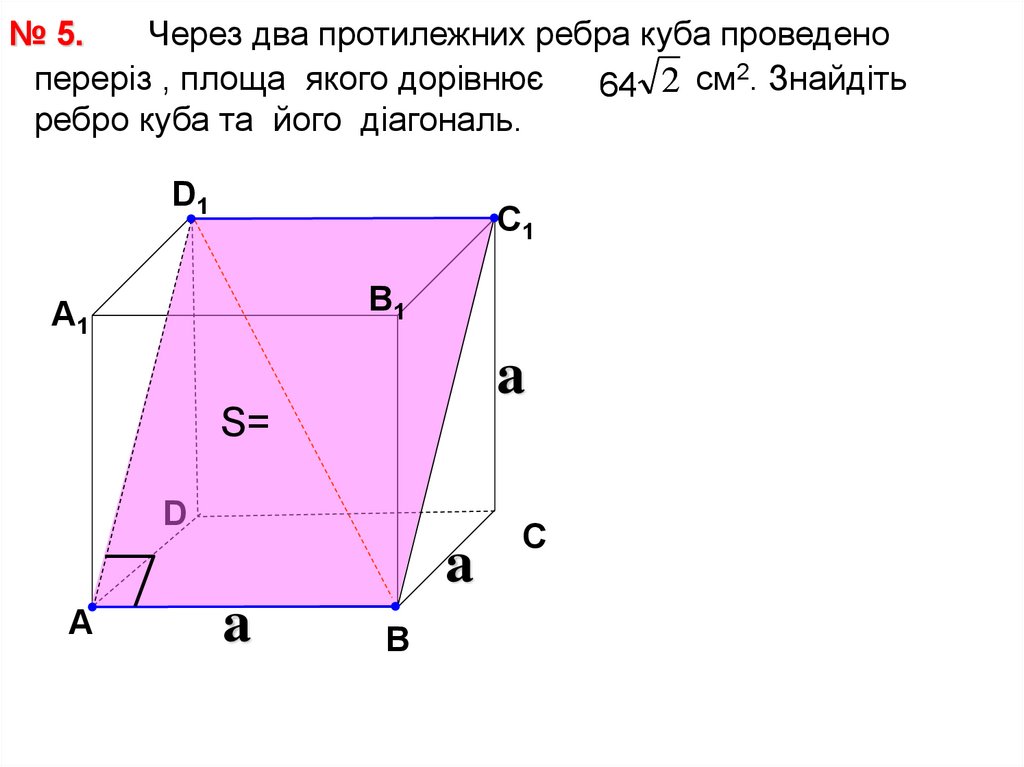
№ 5.Через два протилежних ребра куба проведено
переріз , площа якого дорівнює
64 2 см2. Знайдіть
ребро куба та його діагональ.
D1
С1
В1
А1
a
S=
D
a
А
a
В
С
14.
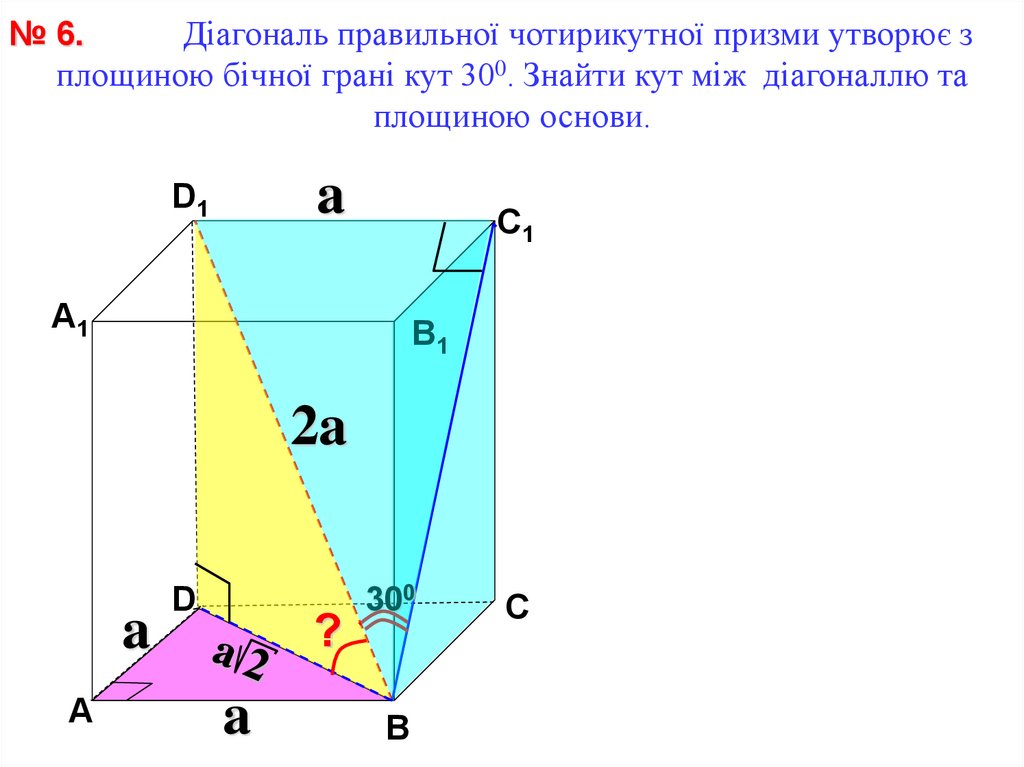
Діагональ правильної чотирикутної призми утворює з№ 6.
площиною бічної грані кут 300. Знайти кут між діагоналлю та
площиною основи.
a
D1
С1
А1
В1
2a
a
А
D
?
a
300
В
С


 Математика
Математика








