Понятие производной

1. Приращение функции. Средняя скорость изменения функции. Понятие производной функции в точке

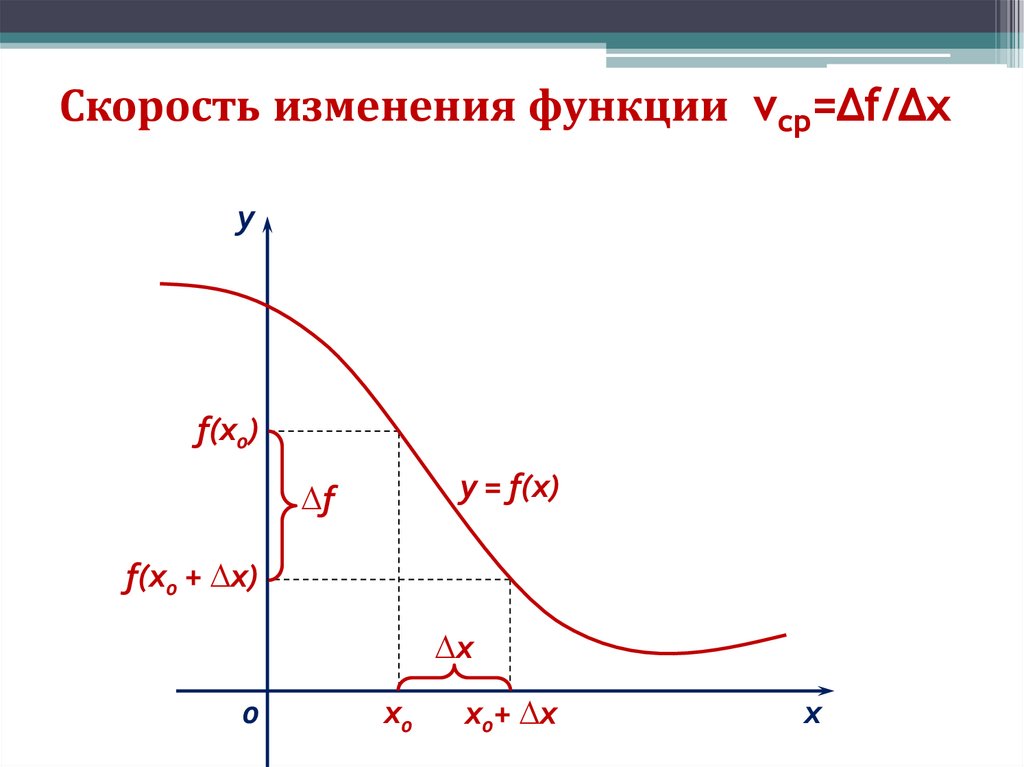
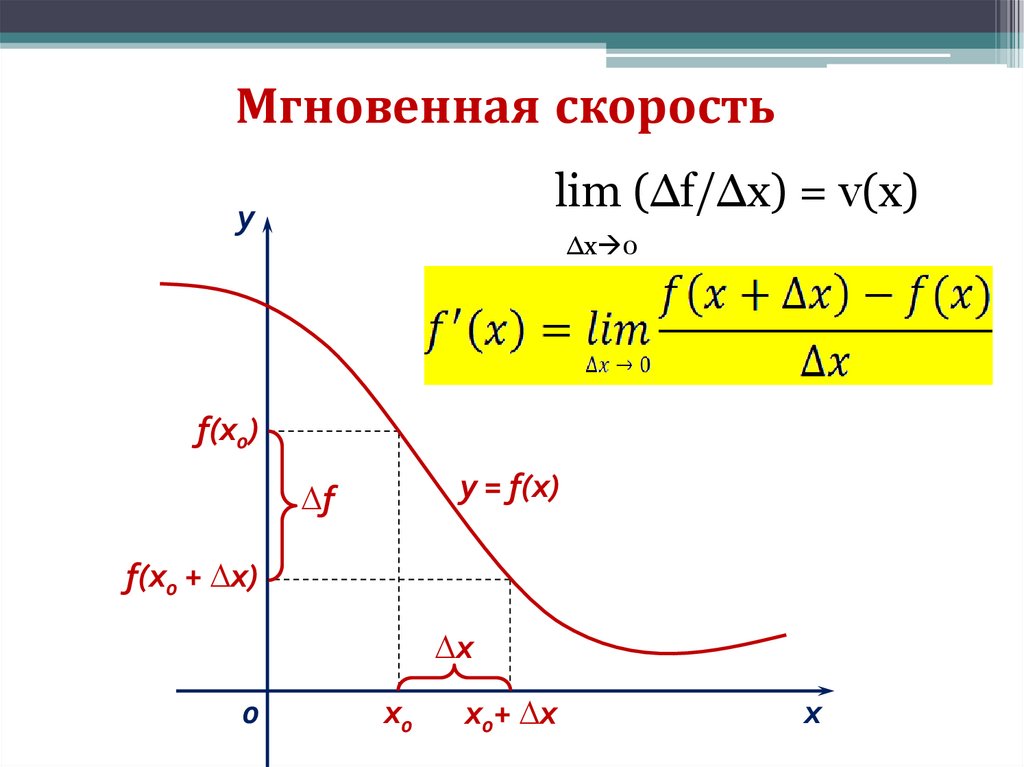
Алгебра 10-11 класс

2. Скорость изменения функции vср=∆f/∆x

у
f(x0)
у = f(x)
∆f
f(x0 + ∆х)
∆х
0
х0
х0+ ∆х
х

3. Определить значение средней скорости изменения функции на заданном промежутке, используя график функции

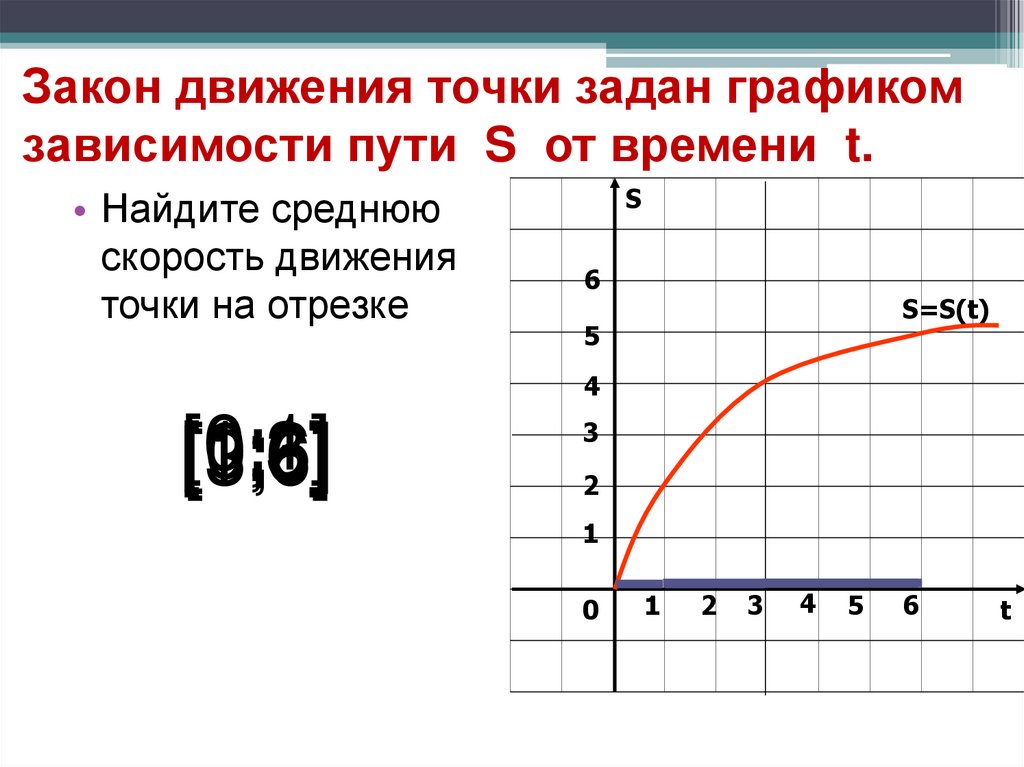
4. Закон движения точки задан графиком зависимости пути S от времени t.

• Найдите среднюю
скорость движения
точки на отрезке
S
6
S=S(t)
5
4
[0;1]
[1;3]
[0;6]
[1;6]
[3;6]
3
2
1
0
1
2
3
4
5
6
t

5. Найти скорость изменения функции у = х³ - х на отрезке [1, 3]

• Приращение аргумента: Δх = 3 – 1 = 2
• Приращение функции:
Δу = у(3) – у(1) =24 – 0 = 24
• Средняя скорость – отношение приращений
Δу : Δх = 24 : 2 = 12

6. Пример 1.

• Найти среднюю скорость изменения функции
y = 0,5 x² на промежутке [1;3].

7. Пример 1.

• Найти среднюю скорость изменения функции
y = 0,5 x² на промежутке [1;3].
• Приращение функции
∆y = f(b) – f(a) =
= 0,5 b² - 0,5 а² = 0,5 · 9 – 0,5 · 1 = 4.
• Приращение аргумента
∆x = b - a = 3 – 1 = 2.
• Средняя скорость
v = ∆y : ∆x = 4 : 2 =2.

8. Пример 2.

• Найти приращение функции y 15 2 x
на промежутке [3; 7] .
• Найти среднюю скорость изменения функции
на этом промежутке.

9. Пример 2.

y 15 2 x
• Найти среднюю скорость изменения функции
на промежутке [3; 7]
y
15 14 15 6 1 3
1
vcp
x
7 3
4
2

10. Пример 3.

• Найти среднюю скорость изменения функции
у = sin( π – x ) на промежутке [π/6; π/2]

11. Пример 3.

• Найти среднюю скорость изменения функции
у = sin( π – x ) на промежутке [π/6; π/2].
5
1
y ( ) sin( ) sin( ) .
6
6
6
2
y ( ) sin( ) 1
2
2
x .
2 6 3
1 1
y 1
2 2
y 1
3
vcp
:
.
x 2 3 2

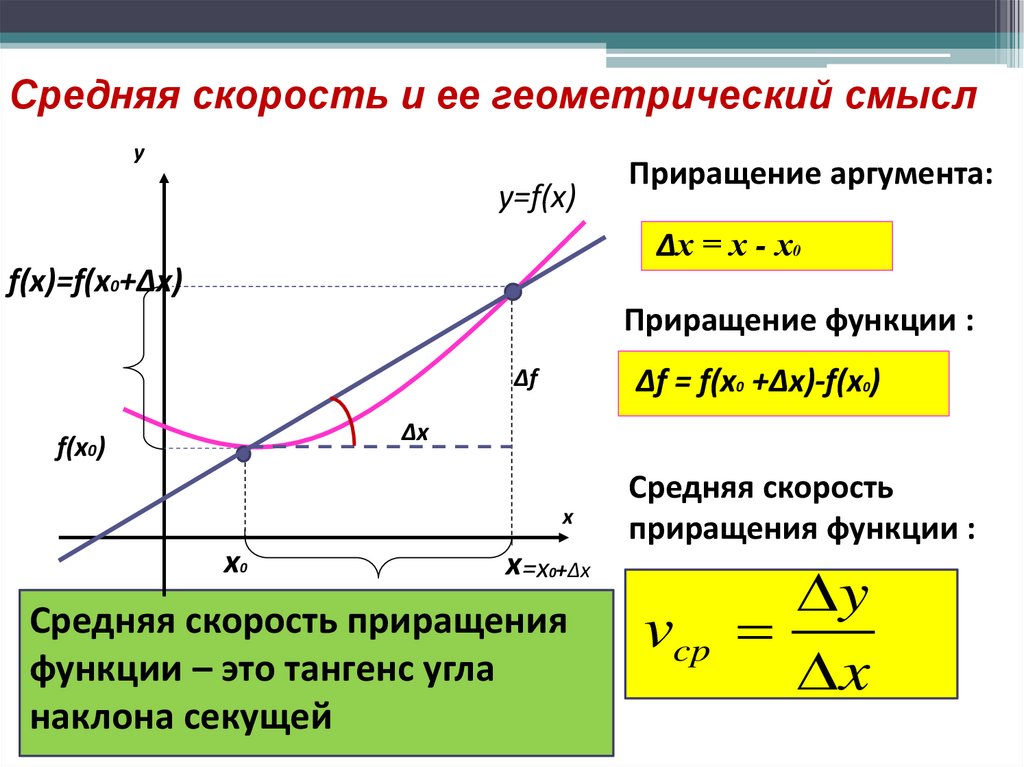
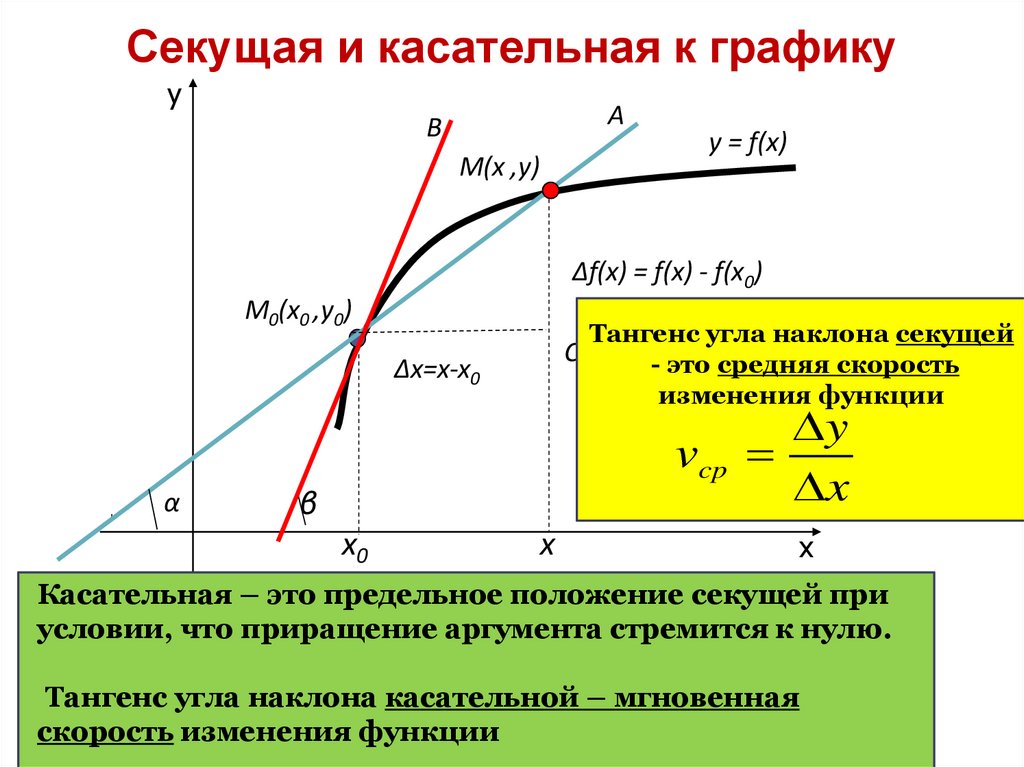
12. Средняя скорость и ее геометрический смысл

y
y=f(x)
Приращение аргумента:
∆х = х - х0
f(x)=f(x0+∆x)
Приращение функции :
∆f = f(x0 +∆x)-f(x0)
∆f
∆x
f(x0)
x
x0
x=x0+∆x
Средняя скорость приращения
функции – это тангенс угла
наклона секущей
Средняя скорость
приращения функции :
y
vcp
x

13. Пример 4.

Найти тангенс угла наклона секущей графика
функции у = 6/х, проведенной через точки
графика с абсциссами х = -1 и х = -3.
y f (b) f (a )
tg
x
b a
y f ( 1) f ( 3) 6 ( 2)
tg
2
x
1 ( 3)
2

14. Пример 5.

Найдите угол наклона секущей к графику
функции y = cos х, проведенной через точки
графика с абсциссами х = -