Лекция 2. Прямые и плоскости

1.

Лекция 2
Комплексный чертеж точки. Осный и
безосный способы изображения
Комплексные чертежи прямых
линий

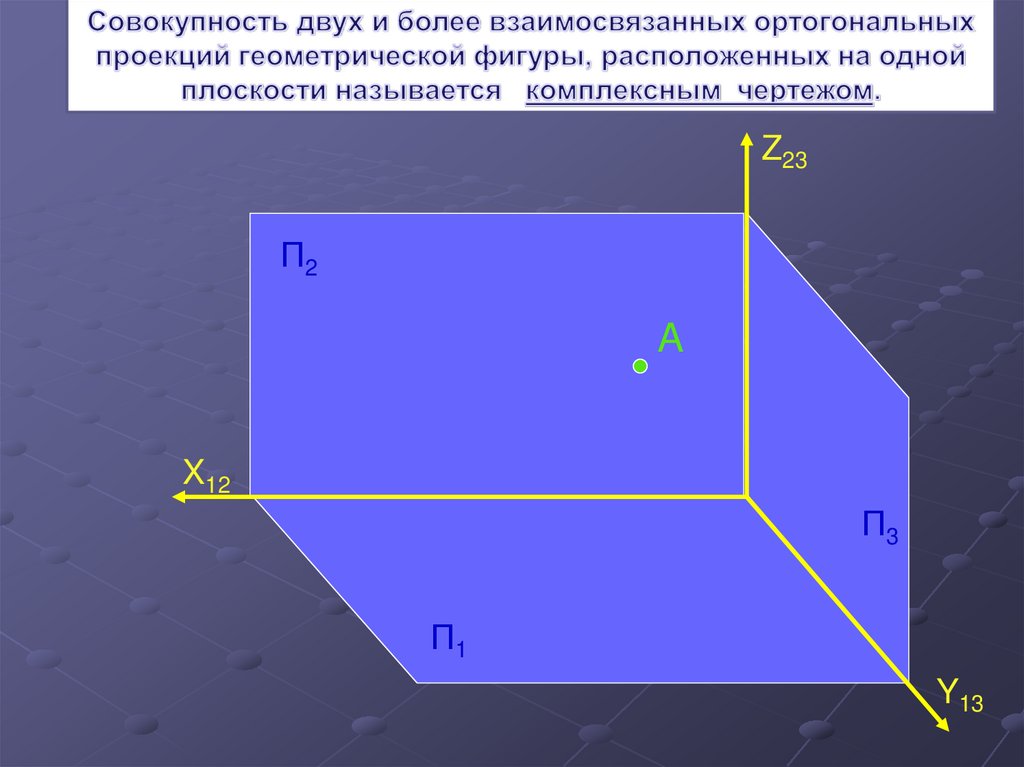
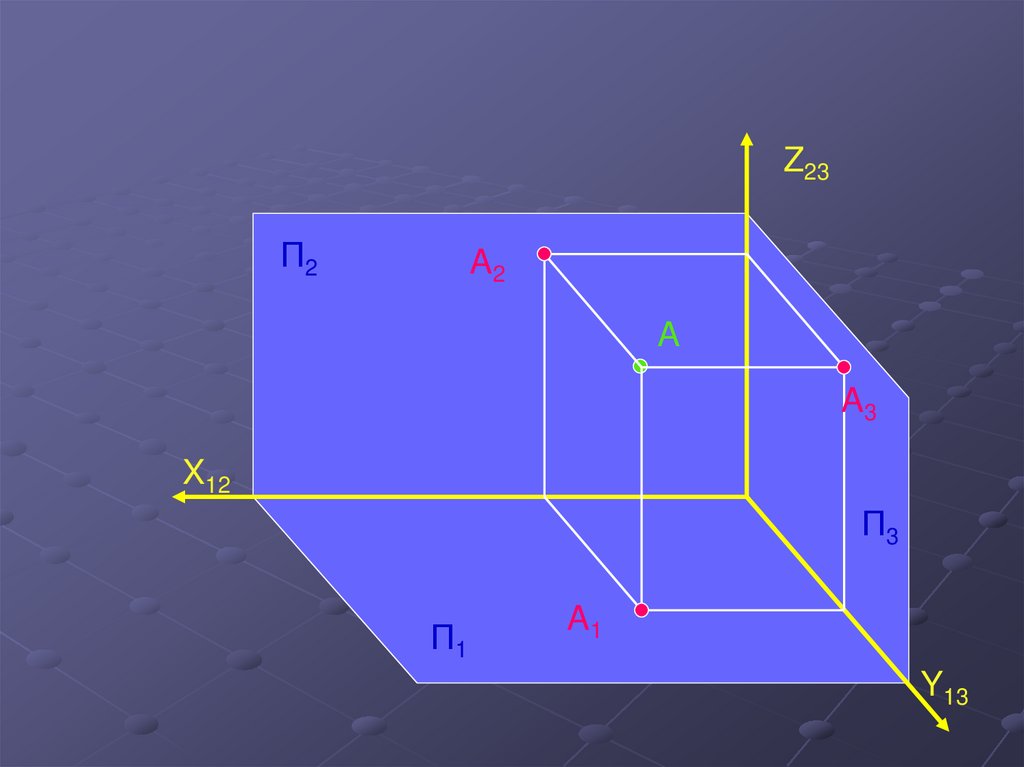
2.

Z23
П2
A
X12
П3
П1
Y13

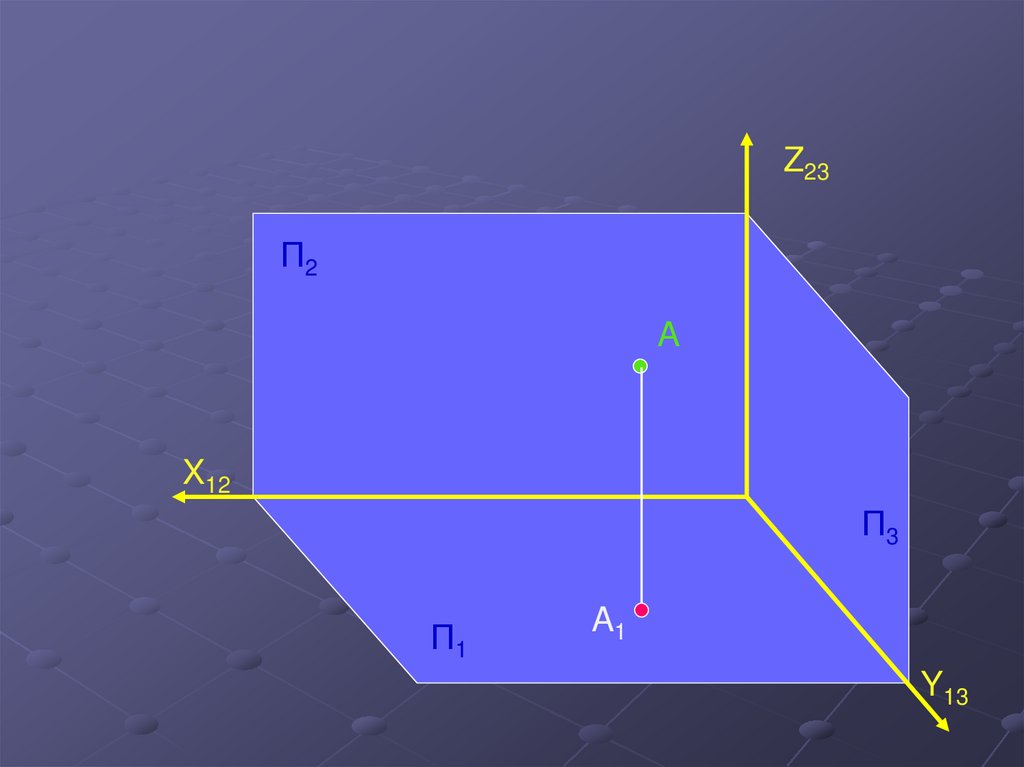
3.

Z23
П2
A
X12
П3
П1
A1
Y13

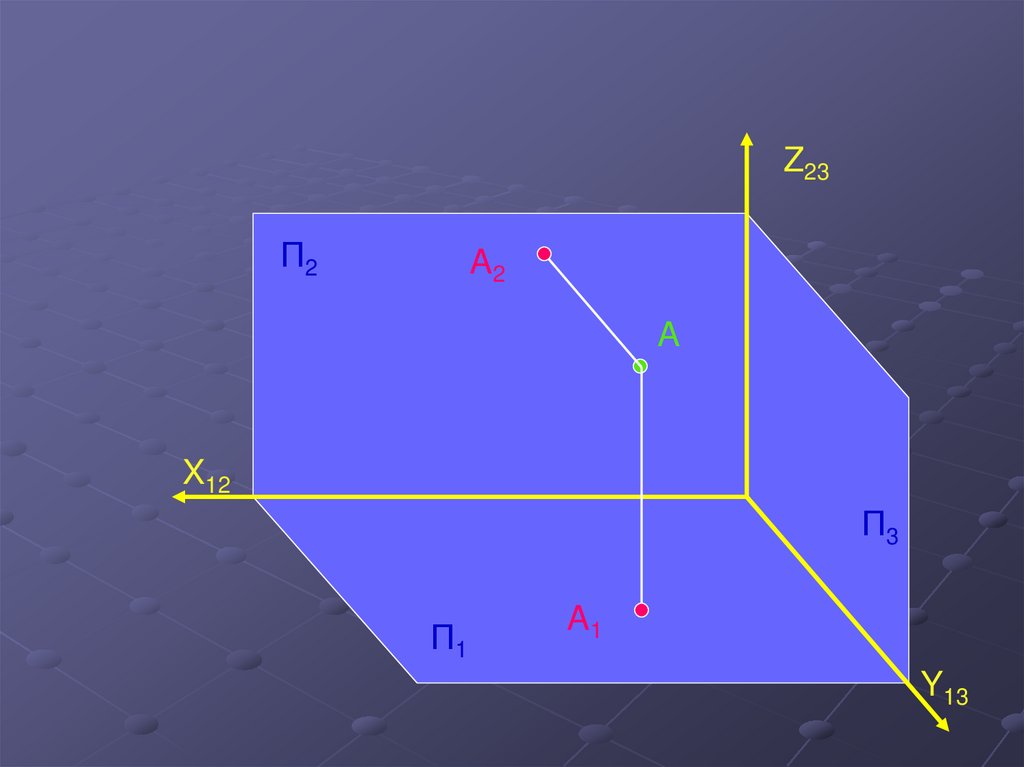
4.

Z23
П2
A2
A
X12
П3
П1
A1
Y13

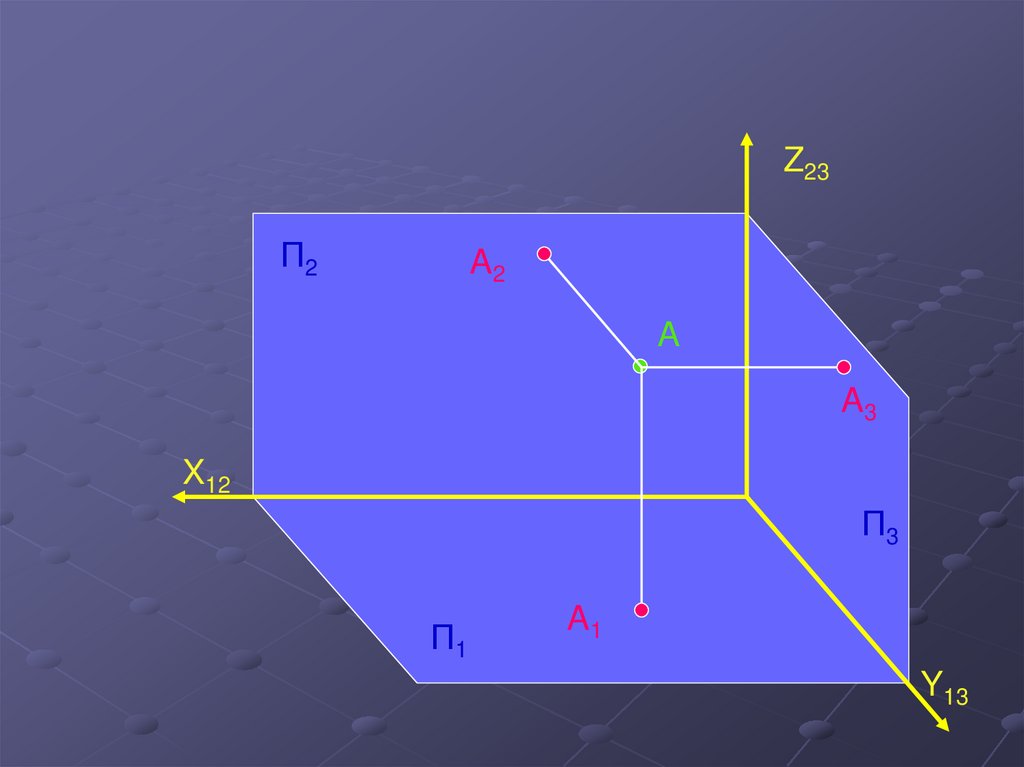
5.

Z23
П2
A2
A
A3
X12
П3
П1
A1
Y13

6.

Z23
П2
A2
A
A3
X12
П3
П1
A1
Y13

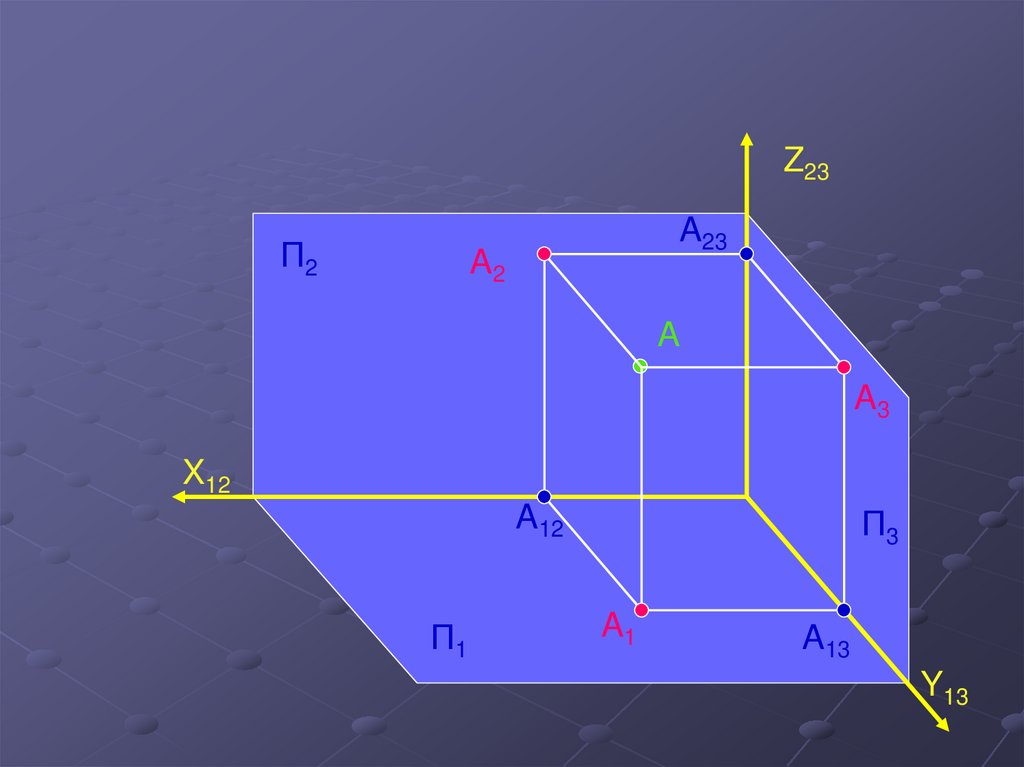
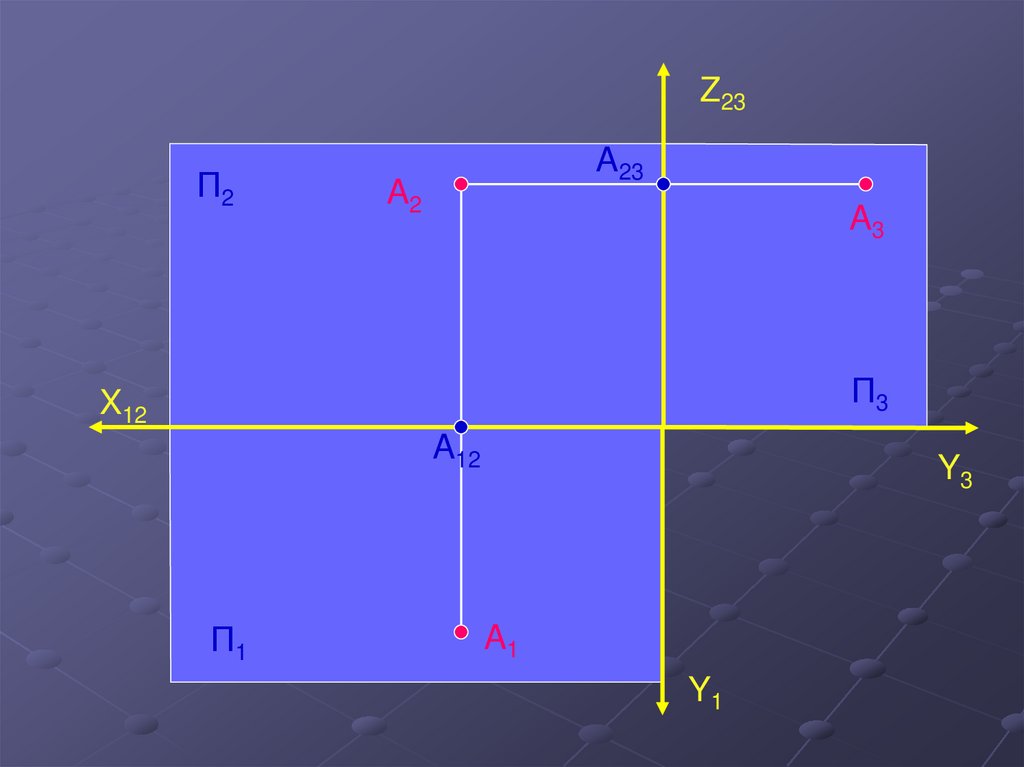
7.

Z23
П2
A23
A2
A
A3
X12
A12
П1
П3
A1
A13
Y13

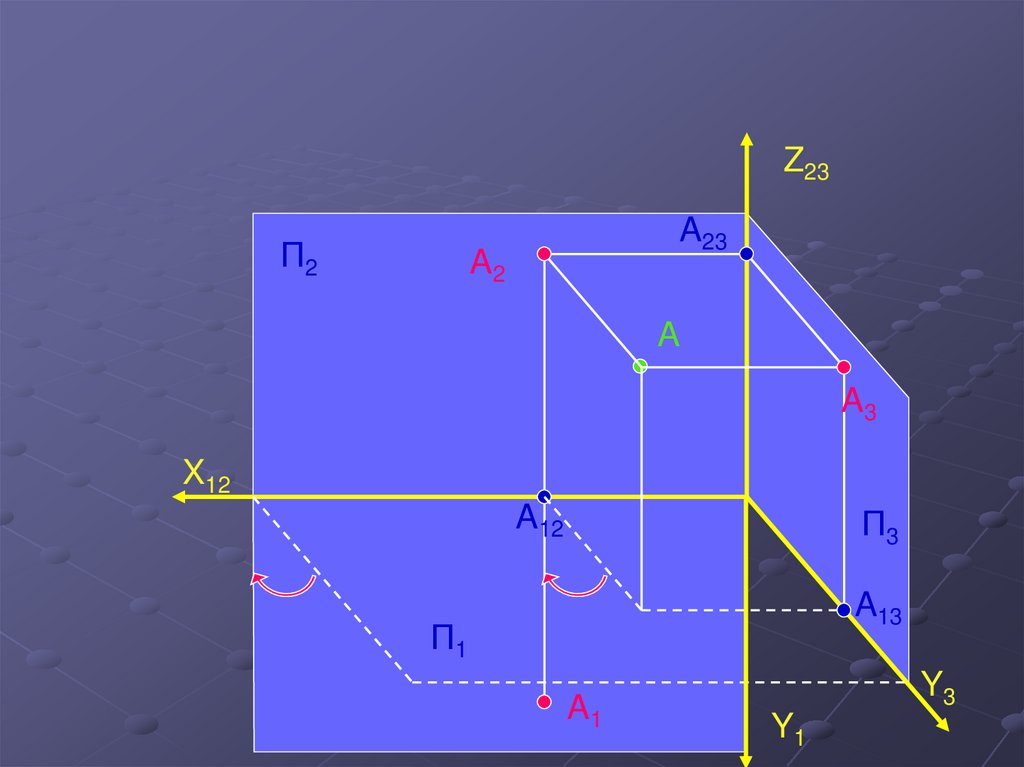
8.

Z23
П2
A23
A2
A
A3
X12
A12
П3
A13
П1
A1
Y3
Y1

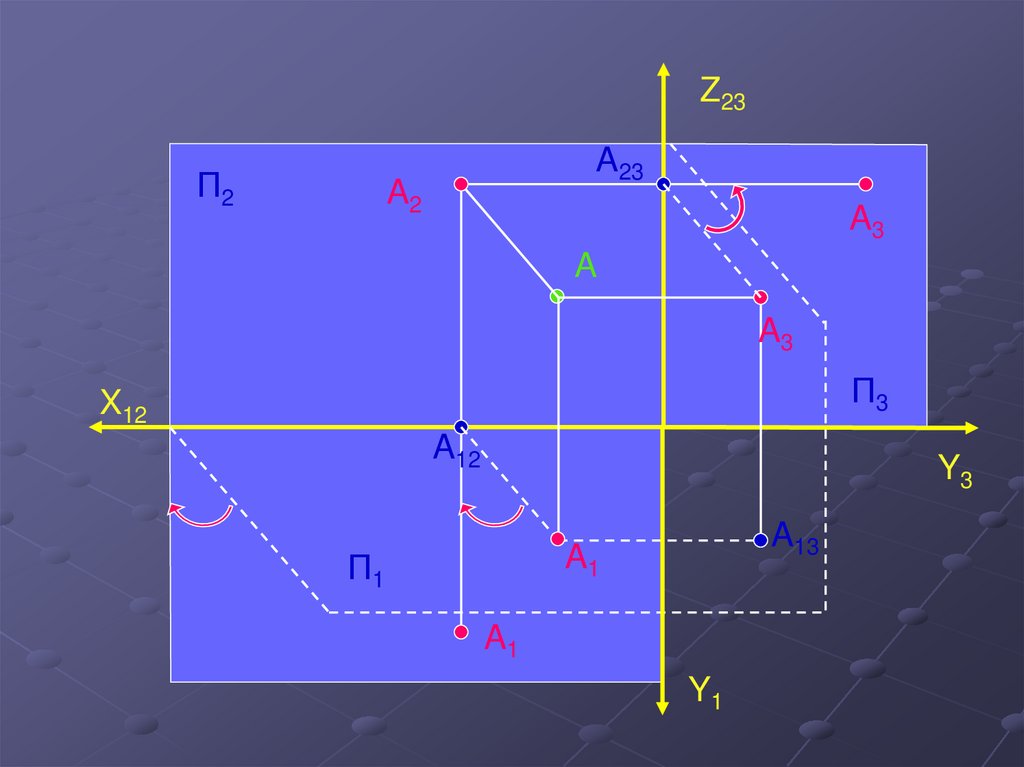
9.

Z23
П2
A23
A2
A3
A
A3
П3
X12
A12
Y3
A13
A1
П1
A1
Y1

10.

Z23
П2
A23
A2
A3
П3
X12
A12
П1
Y3
A1
Y1

11.

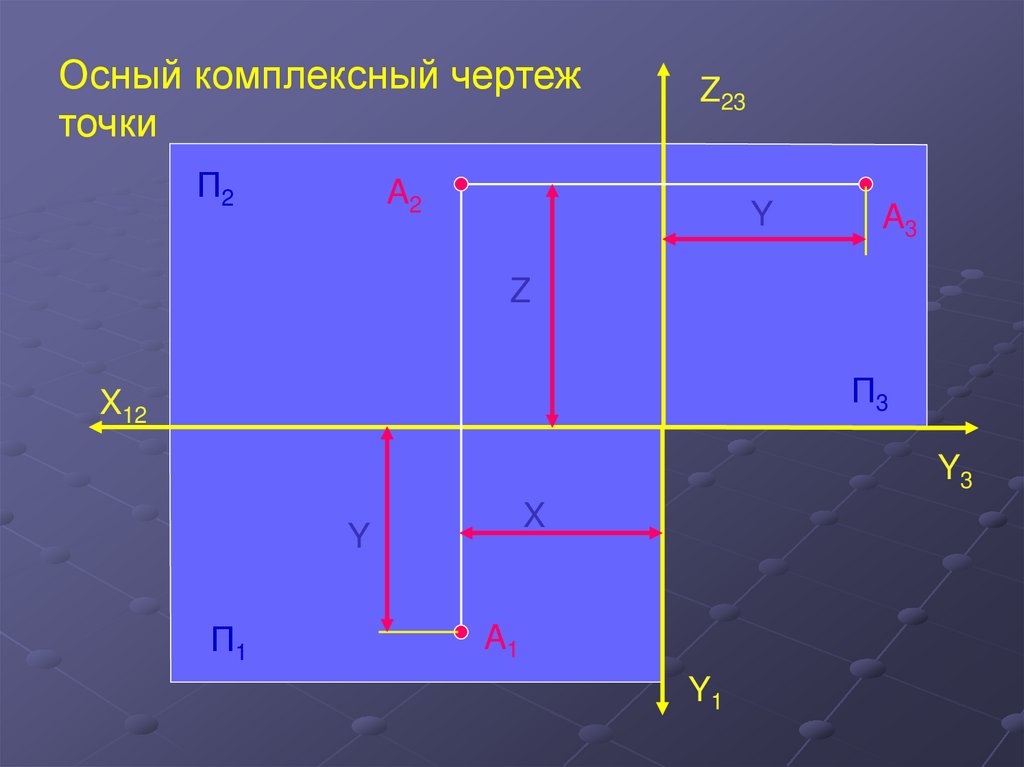
Осный комплексный чертеж
точки
П2
Z23
A2
Y
A3
Z
П3
X12
Y3
X
Y
П1
A1
Y1

12.

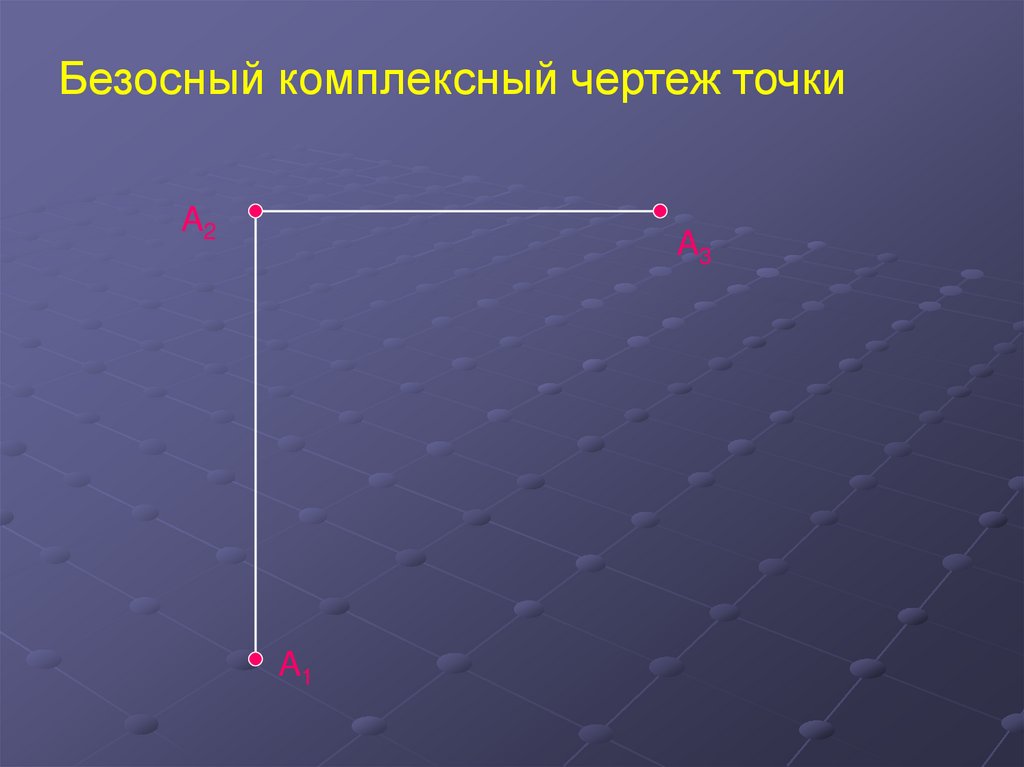
Безосный комплексный чертеж точки
A2
A3
A1

13.

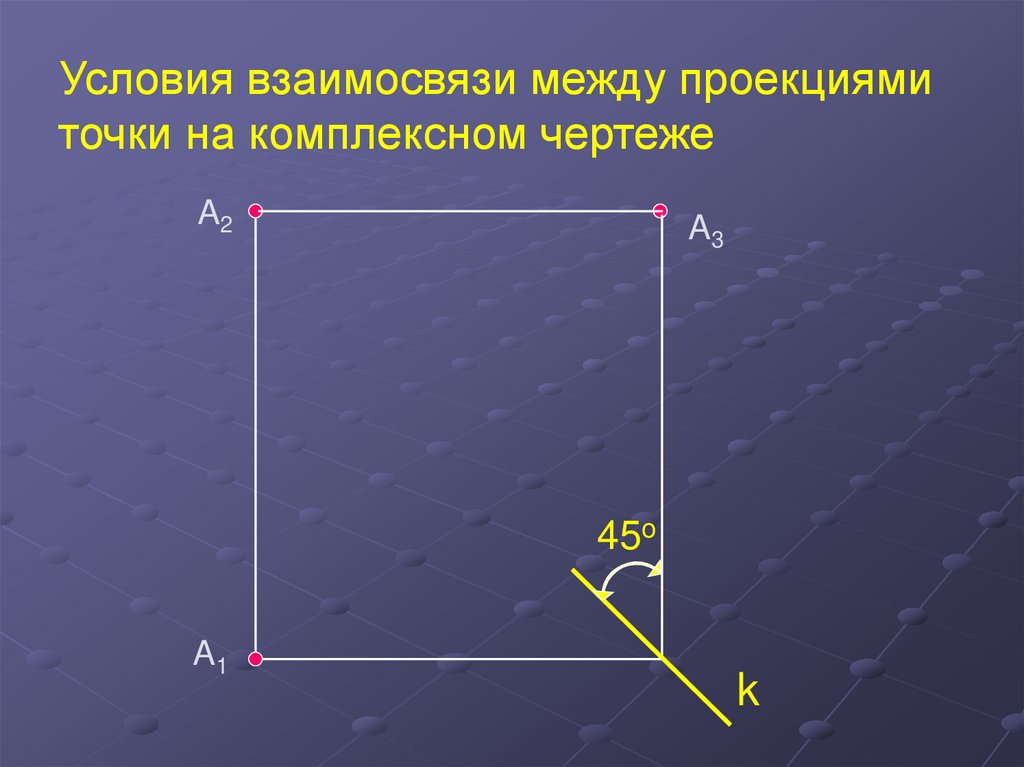
Условия взаимосвязи между проекциями
точки на комплексном чертеже
A2
A3
45o
A1
k

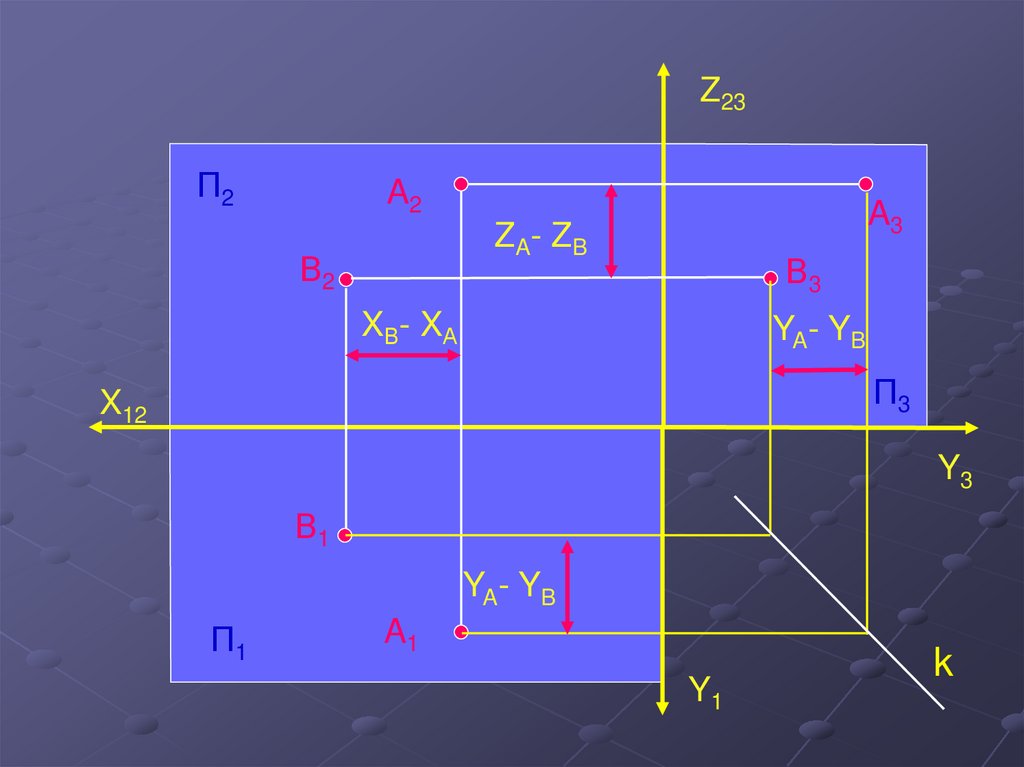
14.

Z23
П2
A2
A3
ZA- ZB
В2
В3
XВ- XА
YA- YB
П3
X12
Y3
В1
YA- YB
П1
A1
Y1
k

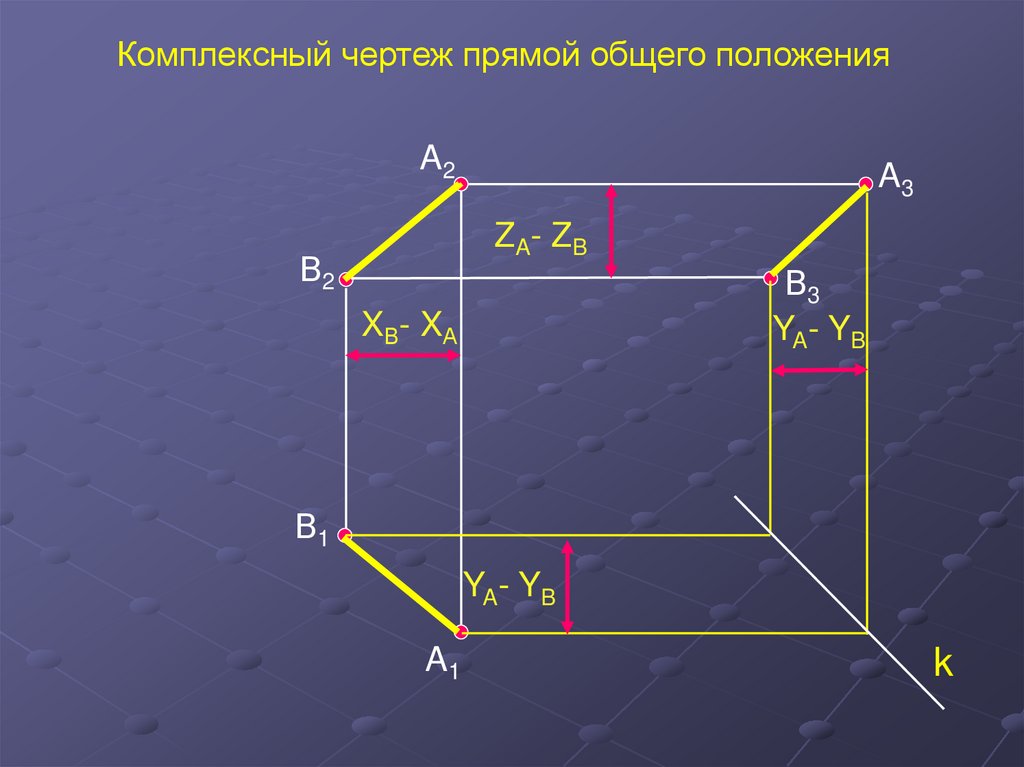
15.

Комплексный чертеж прямой общего положения
A2
A3
ZA- ZB
В2
В3
YA- YB
XВ- XА
В1
YA- YB
A1
k

16. Аксиомы и теоремы, характеризующие свойства прямой линии

Аксиома
Через любые две различные точки
проходит одна и только одна прямая
Теорема
Две различные прямые могут иметь не
более одной общей точки

17. Положение прямых в пространстве

Прямые общего положения- не параллельны и не
перпендикулярны ни одной плоскости проекций
Прямые уровня – параллельны плоскостям проекций
Горизонталь h - параллельна П1
Фронталь f - параллельна П2
Профильная прямая p - параллельна П3
Проецирующие прямые- перпендикулярны плоскостям
проекций
Горизонтально-проецирующая – перпендикулярна П1
Фронтально-проецирующая – перпендикулярна П2
Профильно-проецирующая – перпендикулярна П3

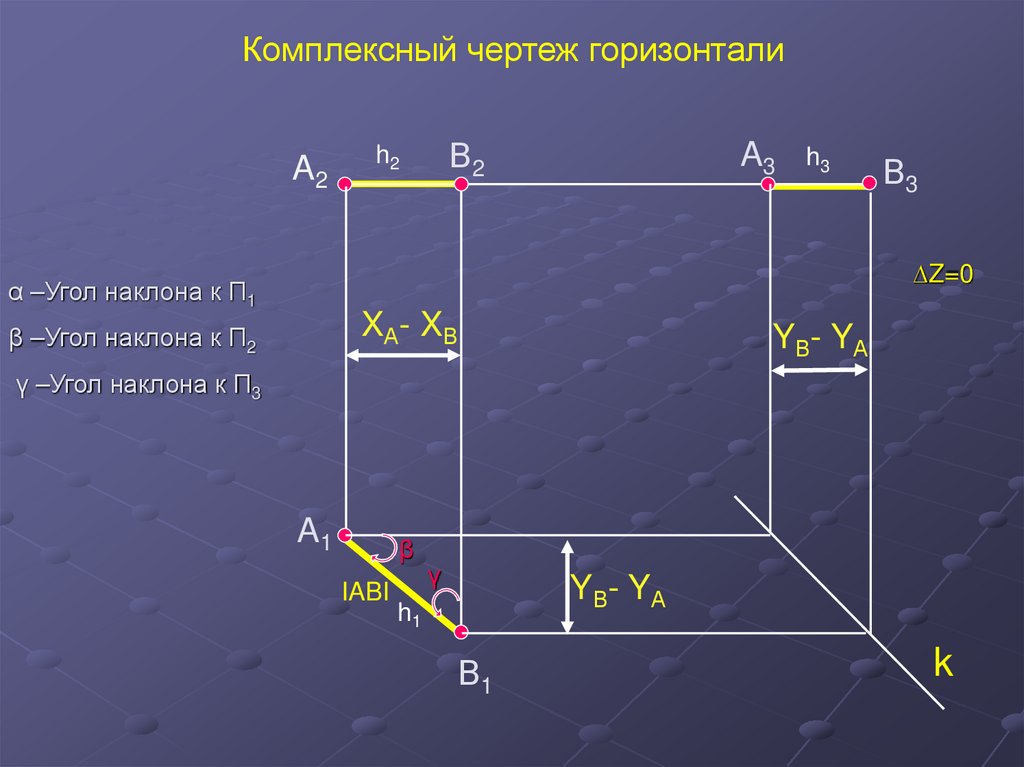
18.

Комплексный чертеж горизонтали
A2
В2
h2
A3
h3
В3
∆Z=0
α –Угол наклона к П1
XА- XВ
β –Угол наклона к П2
YВ- YА
γ –Угол наклона к П3
A1
β
IABI
γ
YВ- YА
h1
В1
k

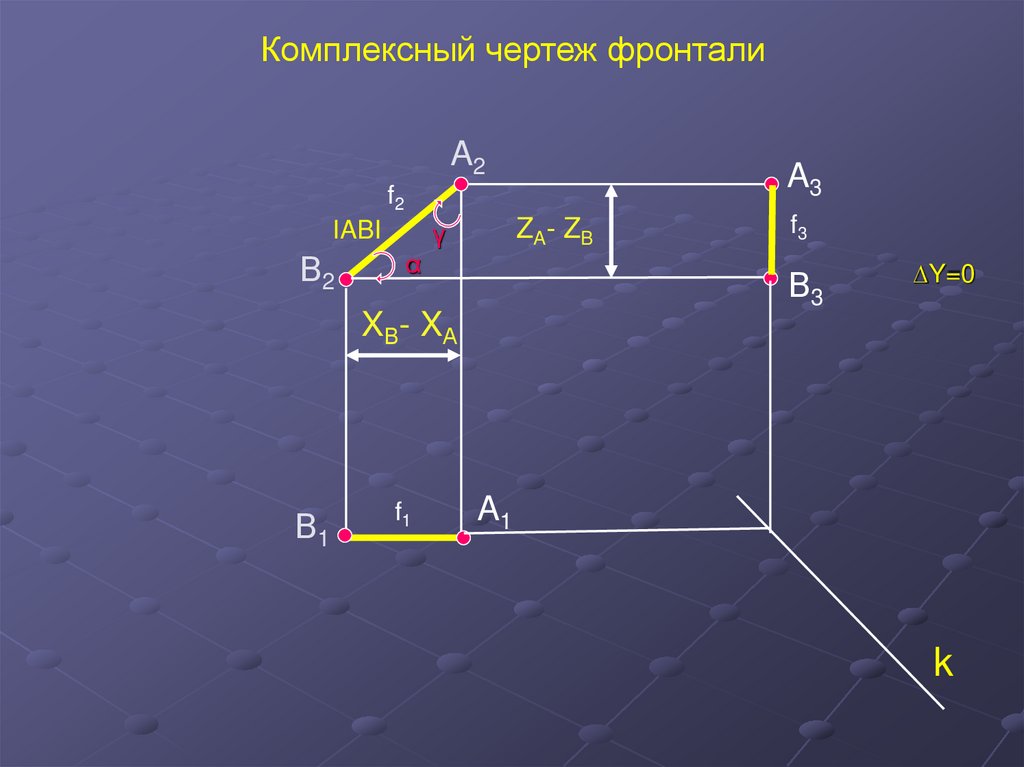
19.

Комплексный чертеж фронтали
A2
A3
f2
В2
ZA- ZB
γ
IABI
α
f3
В3
∆Y=0
XВ- XА
В1
f1
A1
k

20.

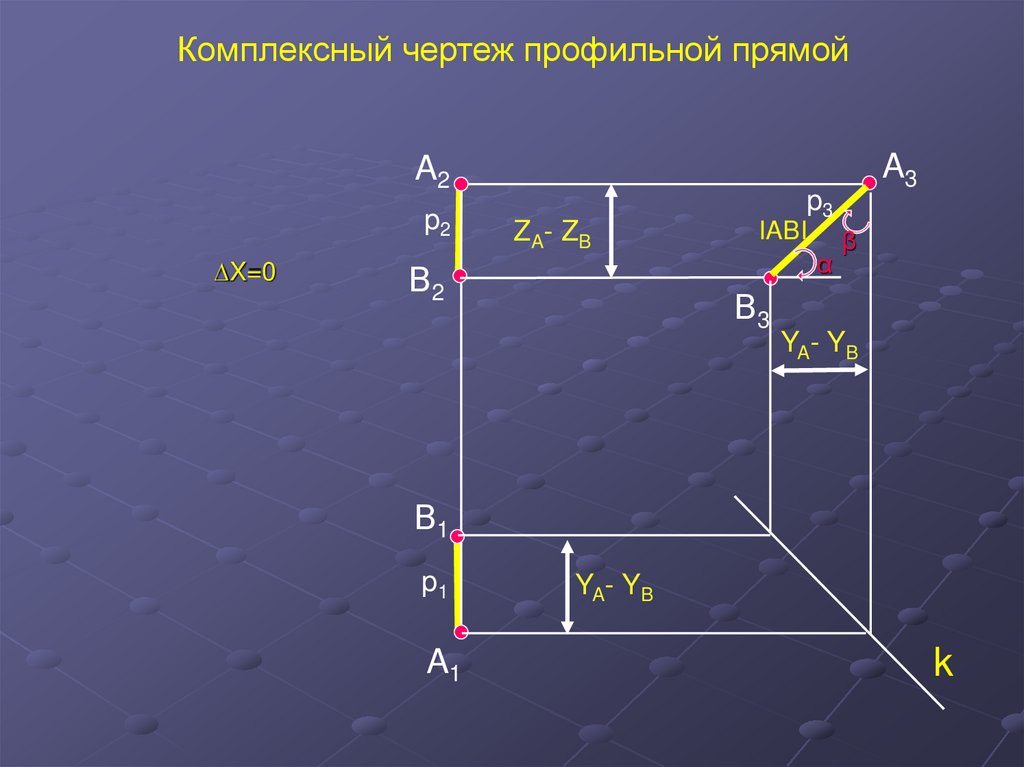
Комплексный чертеж профильной прямой
A2
p2
∆X=0
ZA- ZB
В2
A3
p3
IABI
α
В3
β
YA- YB
В1
p1
A1
YA- YB
k

21.

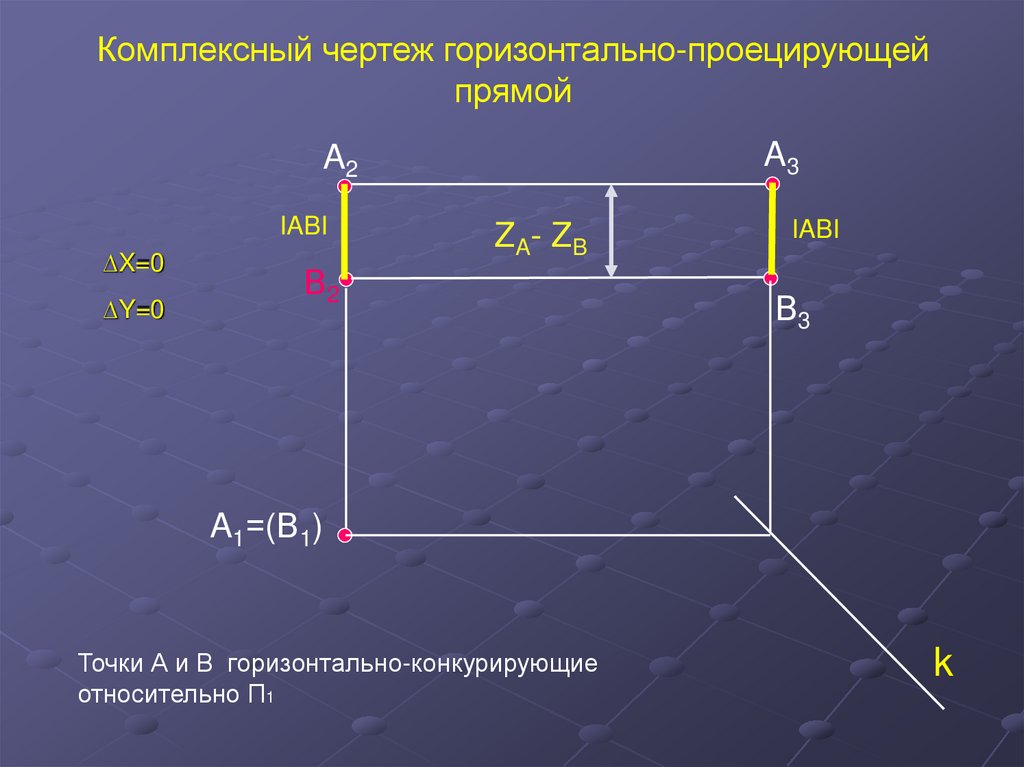
Комплексный чертеж горизонтально-проецирующей
прямой
A3
A2
IABI
∆X=0
∆Y=0
ZA- ZB
В2
IABI
В3
A1=(В1)
Точки А и В горизонтально-конкурирующие
относительно П1
k

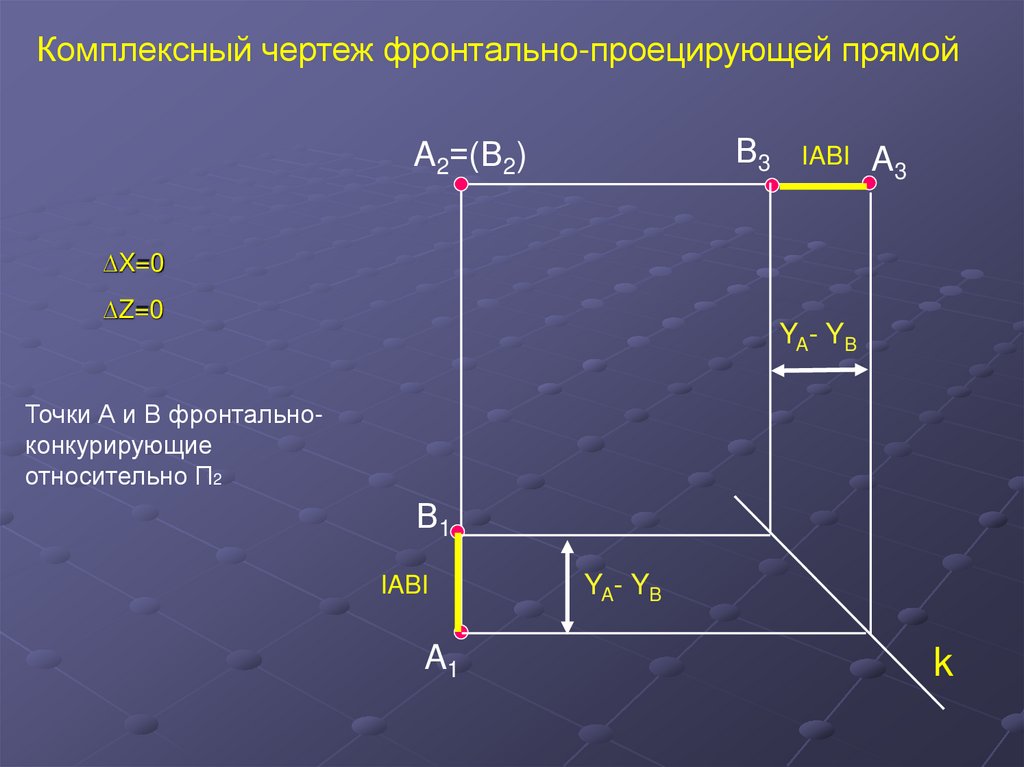
22.

Комплексный чертеж фронтально-проецирующей прямой
В3
A2=(В2)
IABI
A3
∆X=0
∆Z=0
YA- YB
Точки А и В фронтальноконкурирующие
относительно П2
В1
IABI
A1
YA- YB
k

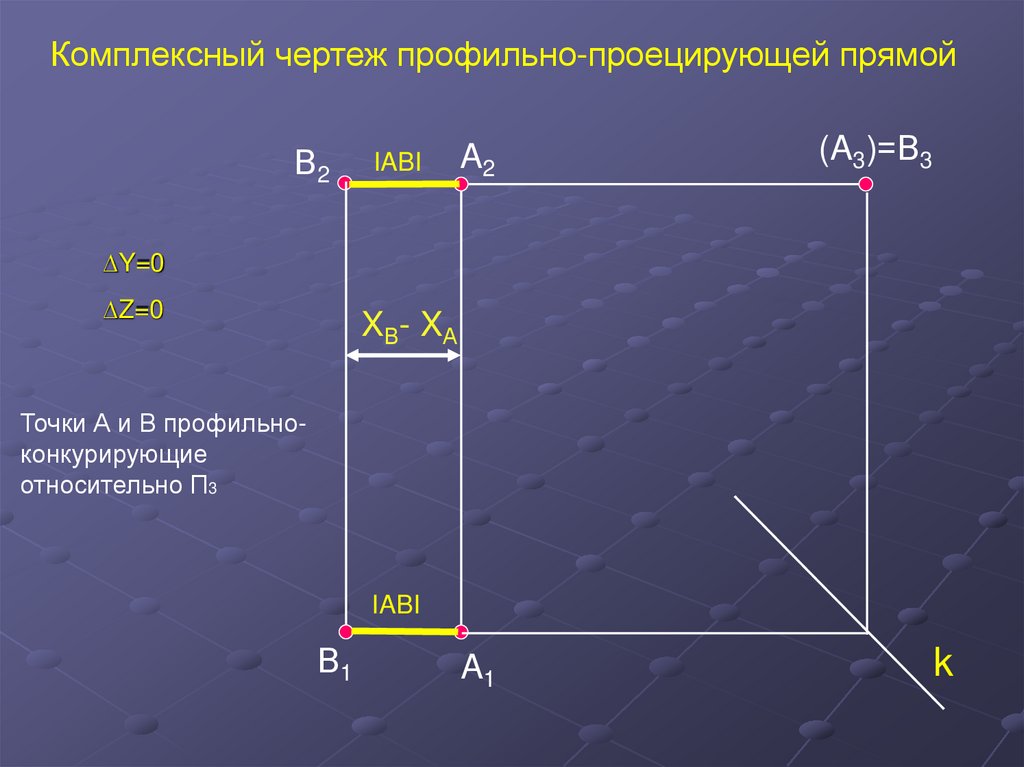
23.

Комплексный чертеж профильно-проецирующей прямой
В2
IABI
A2
(A3)=В3
∆Y=0
∆Z=0
XВ- XА
Точки А и В профильноконкурирующие
относительно П3
IABI
В1
A1
k

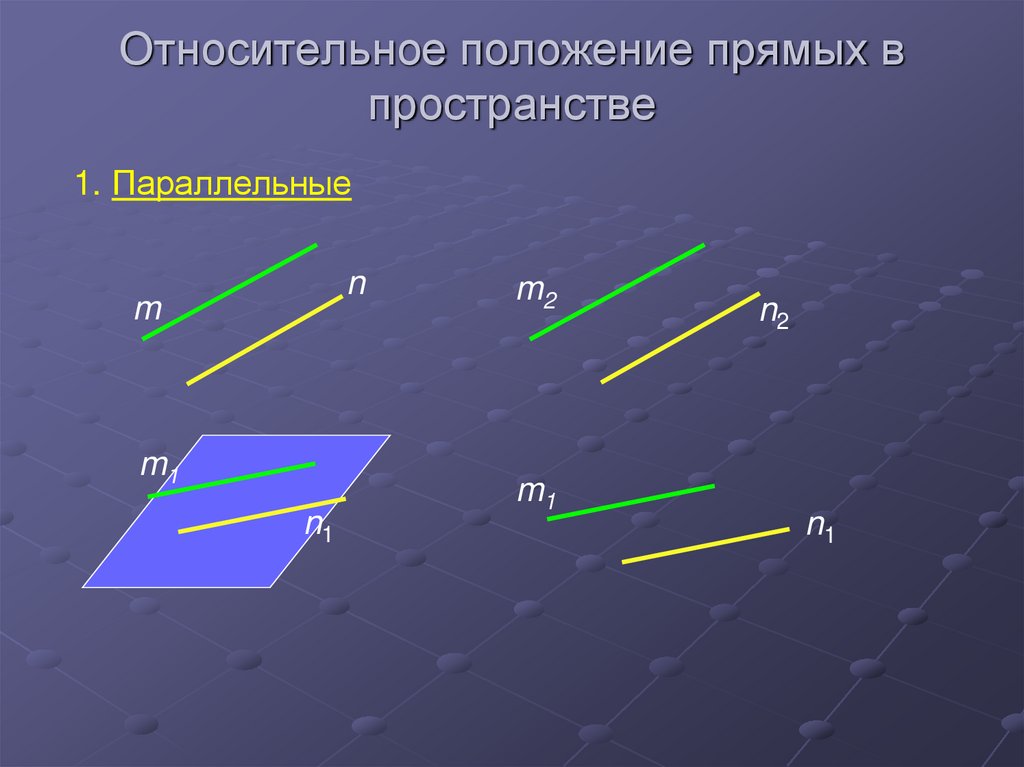
24. Относительное положение прямых в пространстве

1. Параллельные
n
m
m1
n1
m2
m1
n2
n1

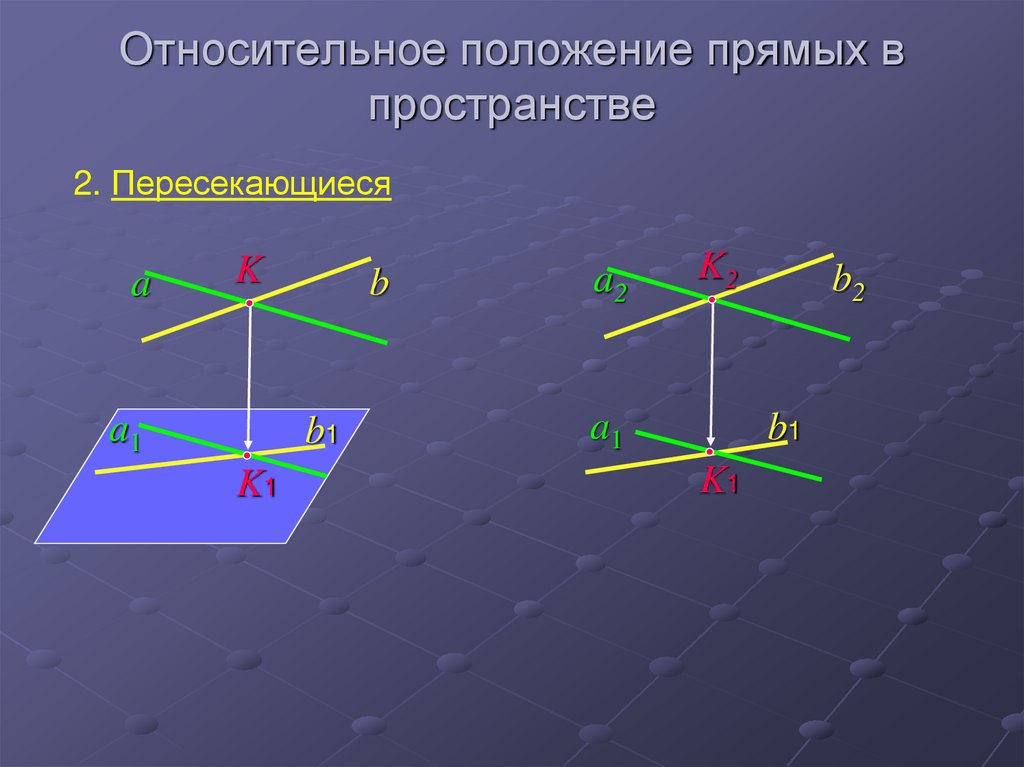
25. Относительное положение прямых в пространстве

2. Пересекающиеся
a
K
a1
b
b1
K1
a2
K2
a1
b2
b1
K1

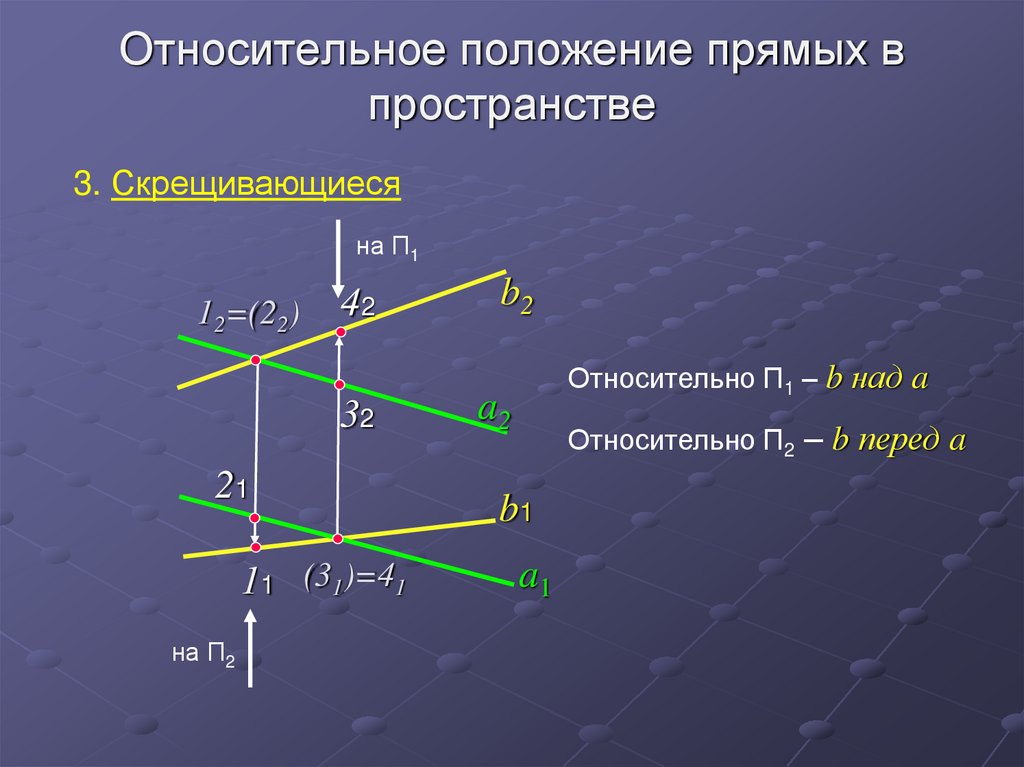
26. Относительное положение прямых в пространстве

3. Скрещивающиеся
на П1
12=(22)
42
32
21
11 (31)=41
на П2
b2
Относительно П1 – b над a
a2
Относительно П2 – b перед a
b1
a1

27. Комплексные чертежи плоскостей

Аксиомы
Через любые три точки не принадлежащие одной
прямой проходит одна и только одна плоскость
1.
2.
3.
Следствия
Через прямую и не принадлежащую ей точку проходит
одна и только одна плоскость
Через две пересекающиеся прямые проходит одна и
только одна плоскость
Через две различные параллельные прямые проходит
одна и только одна плоскость
Если две точки прямой принадлежат плоскости, то
вся прямая принадлежит плоскости
Две плоскости пересекаются по прямой

28. Принадлежность прямой и точки плоскости

Аксиомы
1.
2.
3.
Если две точки прямой принадлежат плоскости, то
вся прямая принадлежит плоскости
Прямая принадлежит плоскости, если она имеет
одну общую точку с плоскостью и параллельна
какой-либо прямой, принадлежащей плоскости
Точка принадлежит плоскости, если через нее
можно провести прямую, принадлежащую
плоскости

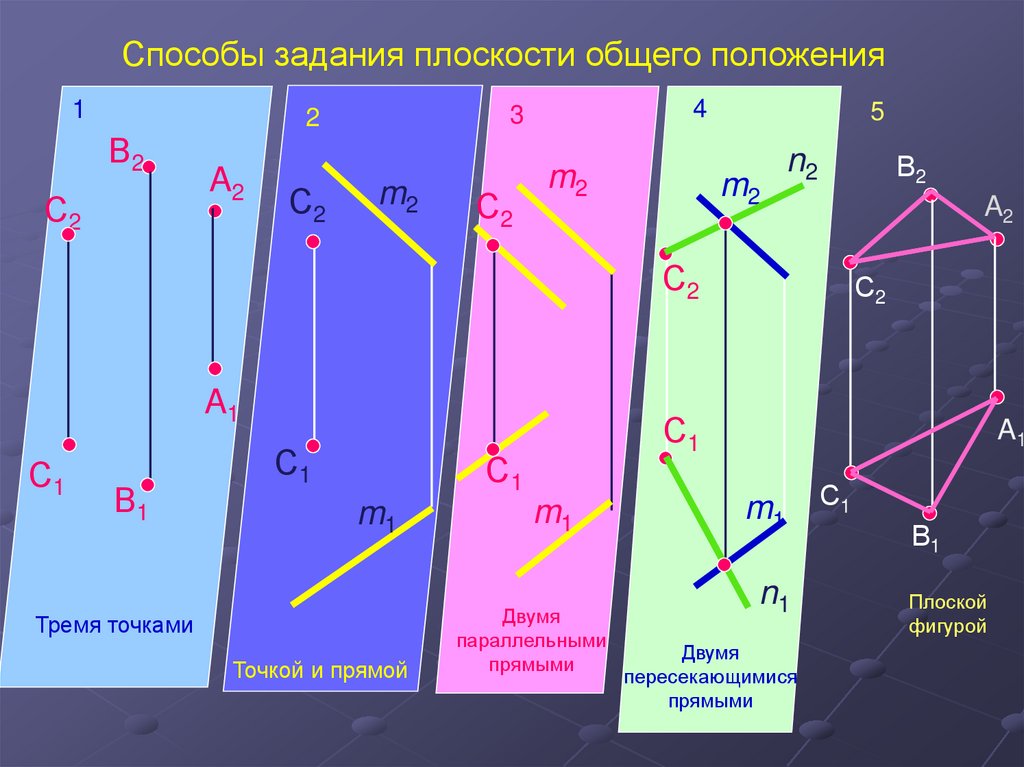
29.

Способы задания плоскости общего положения
1
В2
С2
A2
С2
4
3
2
m2
С2
m2
5
m2
n2
В2
A2
С2
A1
С1
В1
С1
С1
С1
m1
Тремя точками
Точкой и прямой
С2
m1
Двумя
параллельными
прямыми
A1
m1
n1
Двумя
пересекающимися
прямыми
С1
В1
Плоской
фигурой

30. Положение плоскостей в пространстве

Плоскости общего положения- не параллельны и не
перпендикулярны ни одной плоскости проекций
Плоскости уровня – параллельны плоскостям проекций
Горизонтальная пл-ть уровня - параллельна П1
Фронтальная пл-ть уровня - параллельна П2
Профильная пл-ть уровня - параллельна П3
Проецирующие плоскости - перпендикулярны плоскостям
проекций
Горизонтально-проецирующая – перпендикулярна П1
Фронтально-проецирующая – перпендикулярна П2
Профильно-проецирующая – перпендикулярна П3

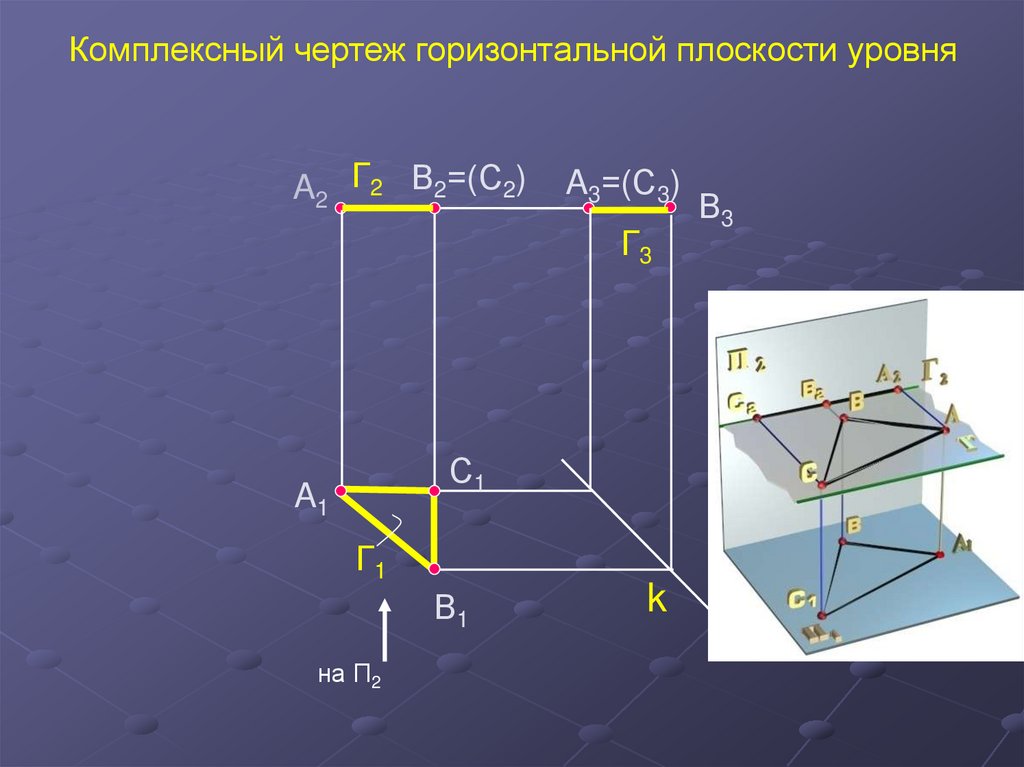
31.

Комплексный чертеж горизонтальной плоскости уровня
A2 Г2 В2=(С2)
A3=(С3)
Г3
С1
A1
Г1
В1
на П2
k
В3

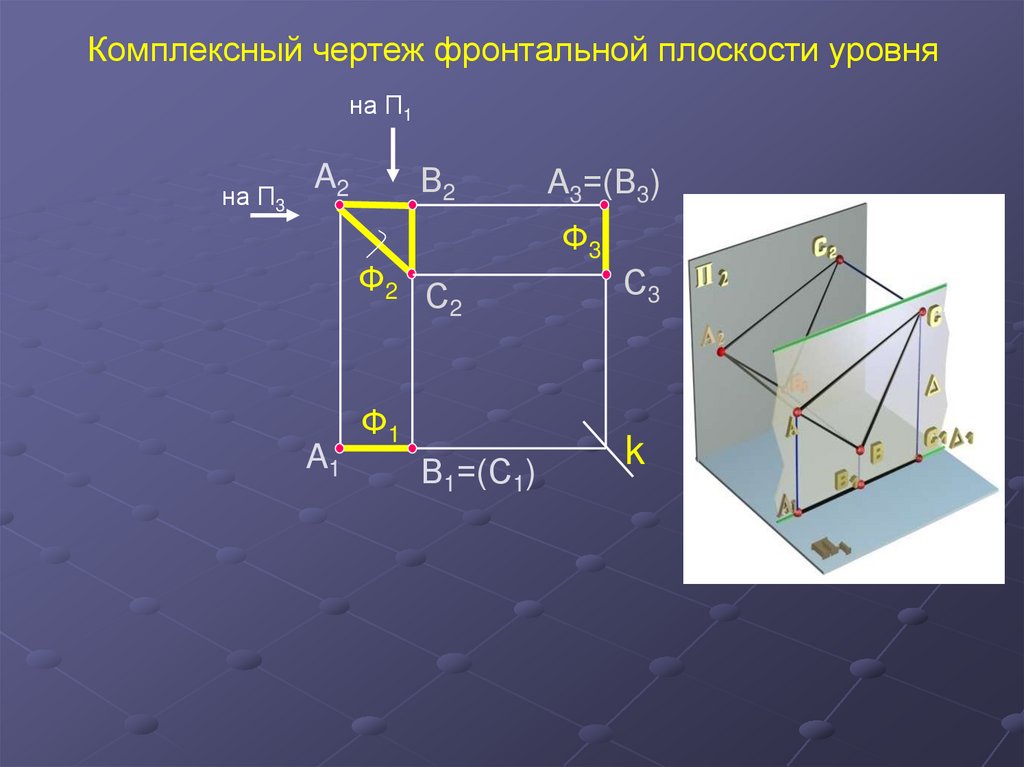
32.

Комплексный чертеж фронтальной плоскости уровня
на П1
на П3
В2
A2
Ф2 С
2
A1
Ф1
В1=(С1)
A3=(В3)
Ф3
С3
k

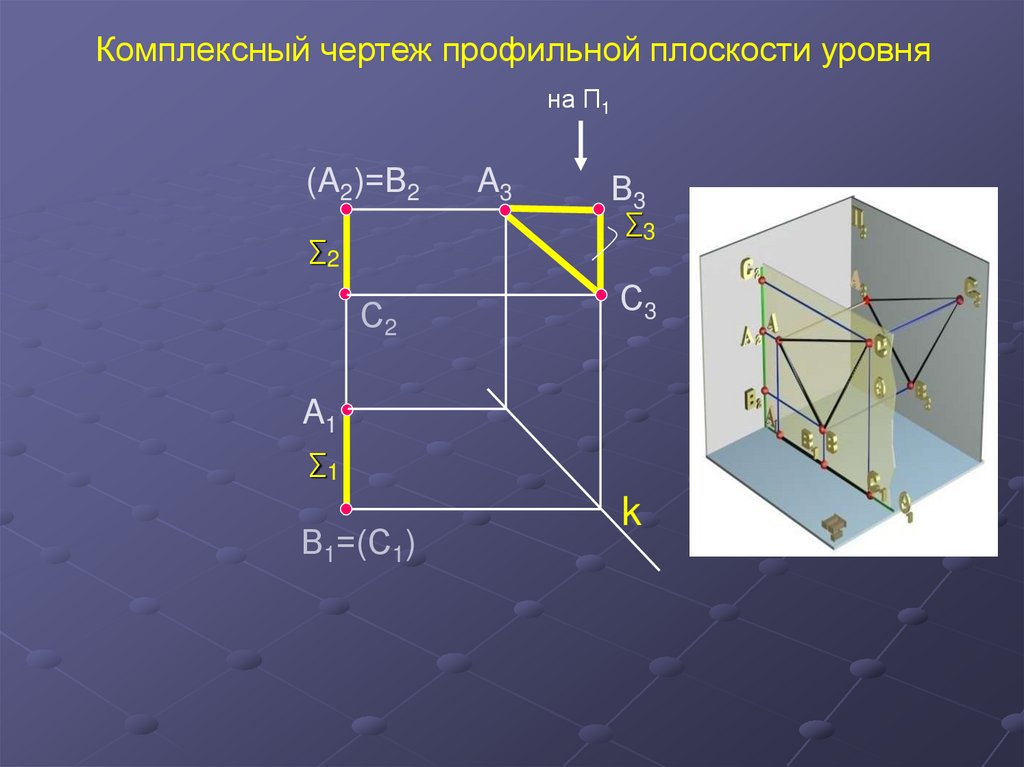
33.

Комплексный чертеж профильной плоскости уровня
на П1
(A2)=В2
A3
В3
∑3
∑2
С2
С3
A1
∑1
В1=(С1)
k

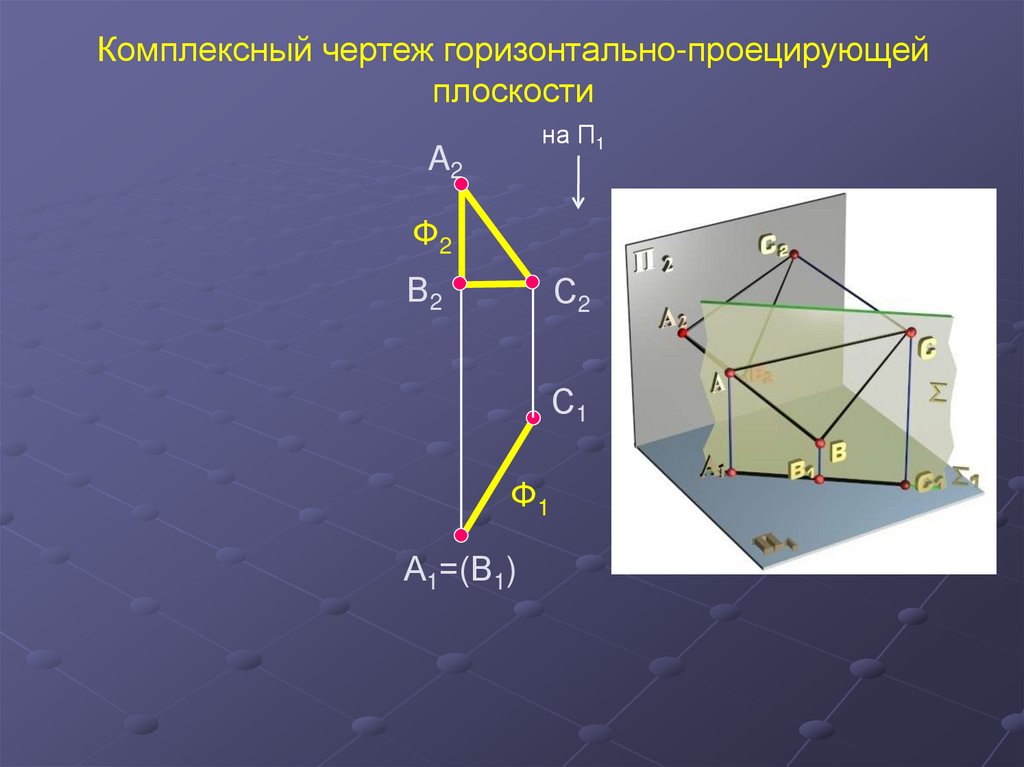
34.

Комплексный чертеж горизонтально-проецирующей
плоскости
на П1
A2
Ф2
В2
С2
С1
Ф1
А1=(В1)

35.

Комплексный чертеж фронтально-проецирующей
плоскости
Ф2
С2
А2=(В2)
В1
A1
Ф1
С1

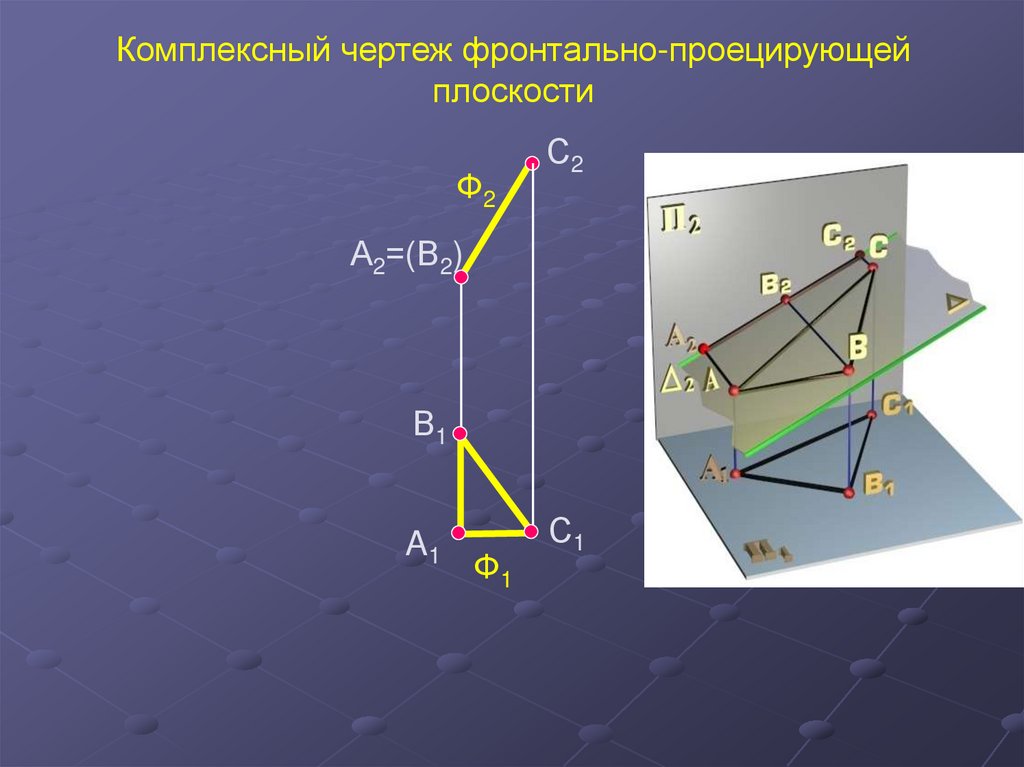
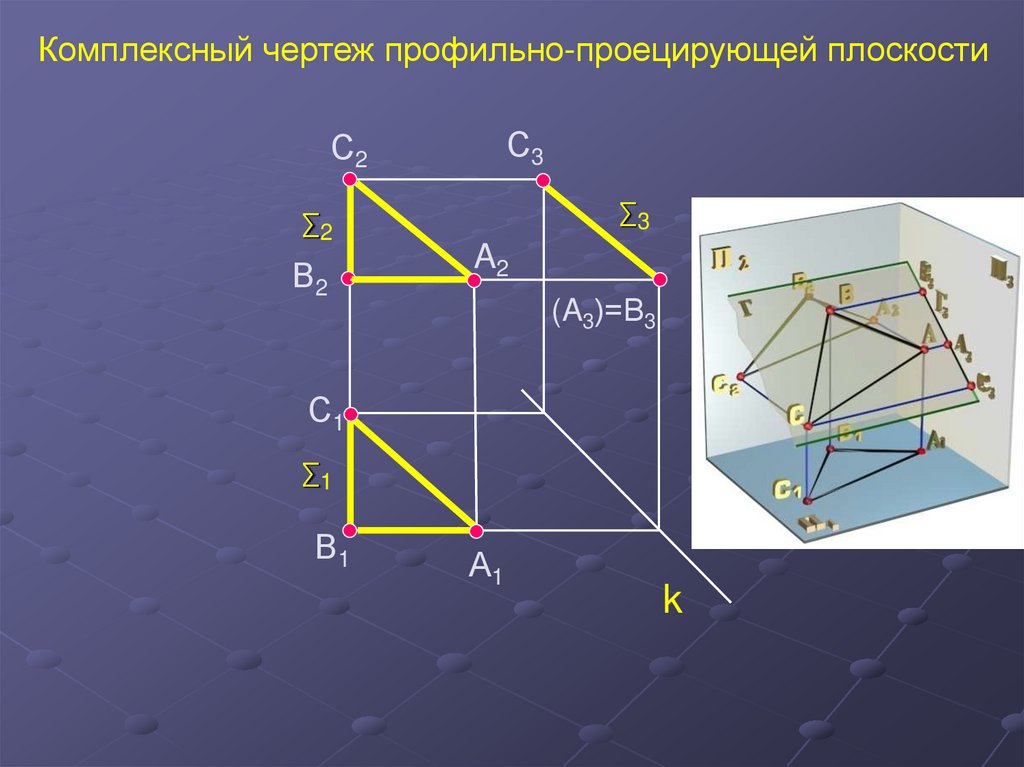
36.

Комплексный чертеж профильно-проецирующей плоскости
С3
С2
∑2
В2
∑3
A2
(A3)=В3
С1
∑1
В1
А1
k