НГ3 прямая (2).1

1.

2.

Проецирование прямой линии
Взаимное положение прямой и точки
Положение прямой относительно плоскостей
проекций
Метод прямоугольного треугольника
Метод поворота вокруг проецирующей оси
Метод замены плоскостей
Взаимное положение двух прямых
Свойство проекций прямого плоского угла

3. Способы задания прямой на эпюре

Координатами 2 точек, принадлежащих
этой прямой
Координатами 1 точки, принадлежащей
прямой и углом наклона этой прямой к
плоскости проекций

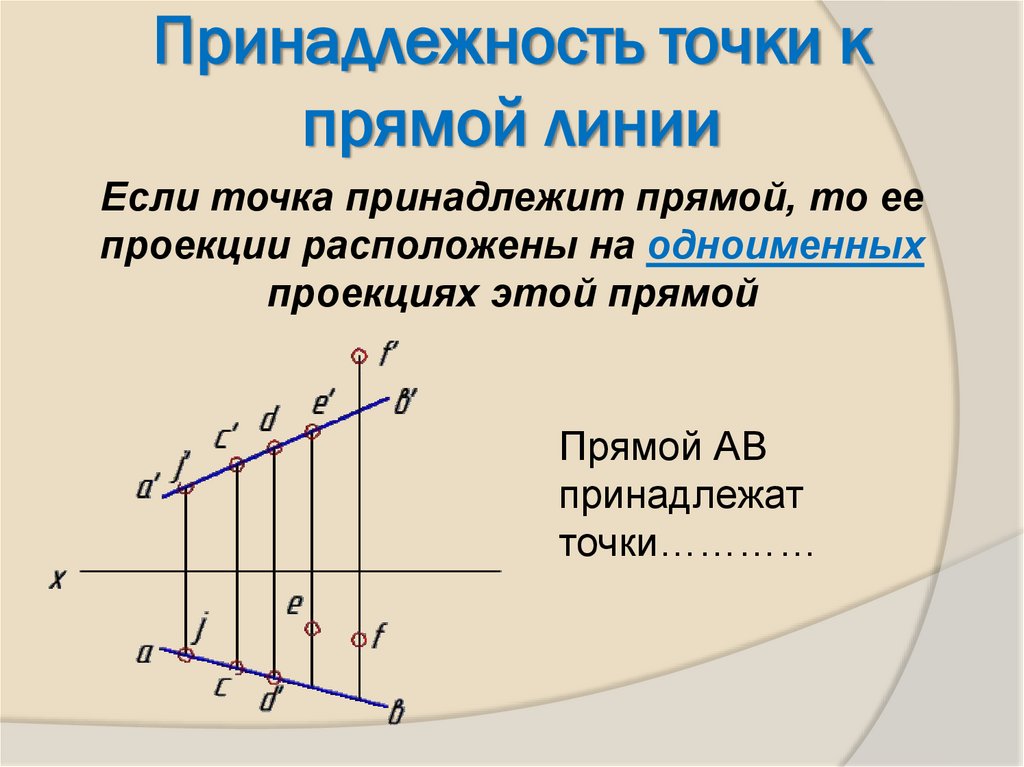
4. Принадлежность точки к прямой линии

Если точка принадлежит прямой, то ее
проекции расположены на одноименных
проекциях этой прямой
Прямой АВ
принадлежат
точки…………

5. Положение прямой относительно плоскостей проекций:

1. Параллельно – прямые уровня (горизонталь,
фронталь, профильная прямая)
2. Перпендикулярно – проецирующие прямые
3. Под углом, отличным от прямого – прямые
общего положения

6. Линии уровня

это – прямые, параллельные плоскостям
проекций:
горизонталь (‖ H)
фронталь (‖ V)
профильная прямая (‖ W)

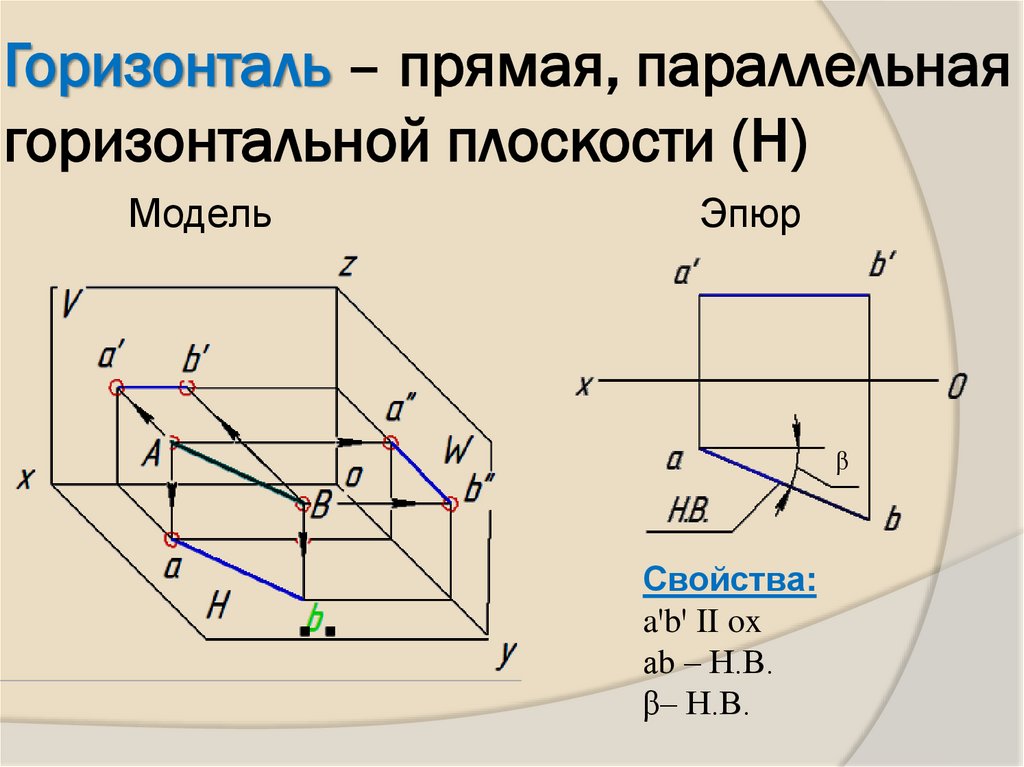
7. Горизонталь – прямая, параллельная горизонтальной плоскости (Н)

Модель
Эпюр
β
Свойства:
aꞌbꞌ II ox
аb – Н.В.
β– Н.В.

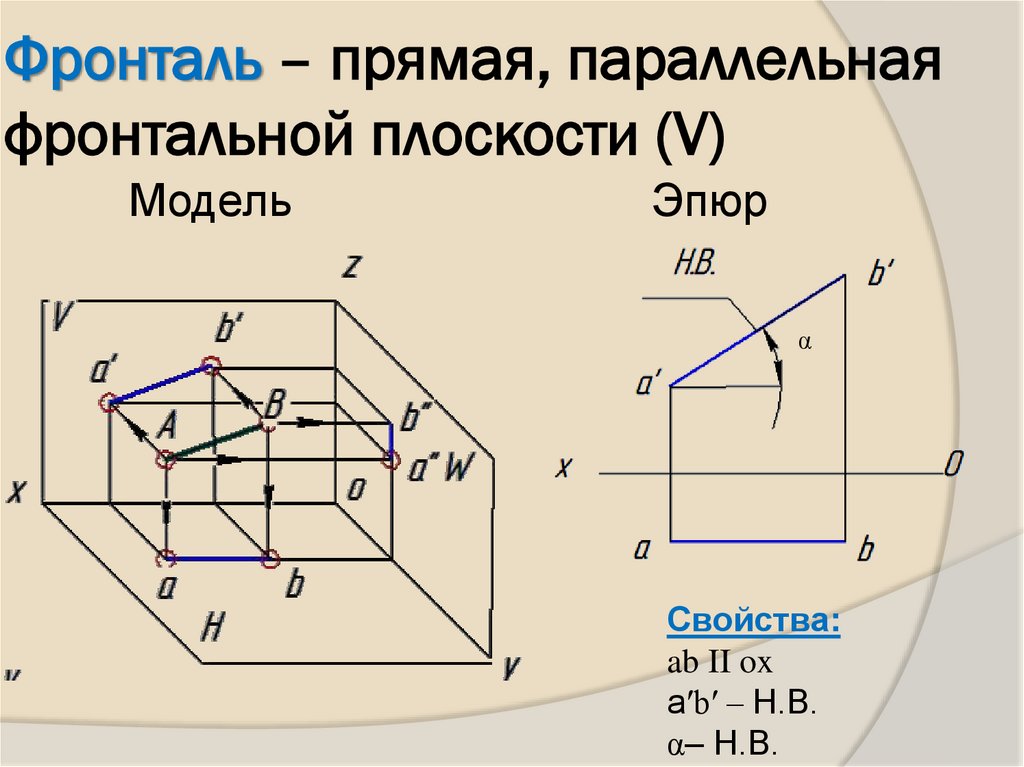
8. Фронталь – прямая, параллельная фронтальной плоскости (V)

Модель
Эпюр
α
Свойства:
ab II ox
аʹbʹ – Н.В.
α– Н.В.

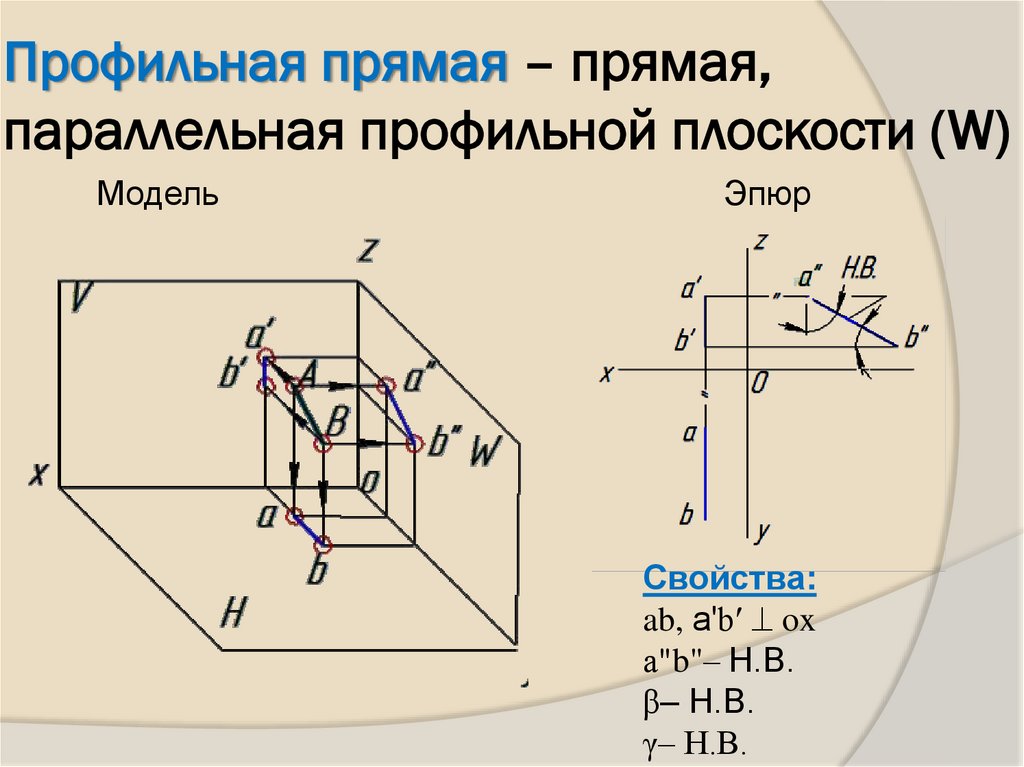
9. Профильная прямая – прямая, параллельная профильной плоскости (W)

Модель
Эпюр
Свойства:
ab, аʹbʹ ox
а"b"– Н.В.
β– Н.В.
γ– Н.В.

10. Проецирующие прямые

Это прямые перпендикулярные к плоскостям
проекций:
горизонтально-проецирующая (┴ H)
фронтально-проецирующая (┴ V)
профильно-проецирующая (┴ W)

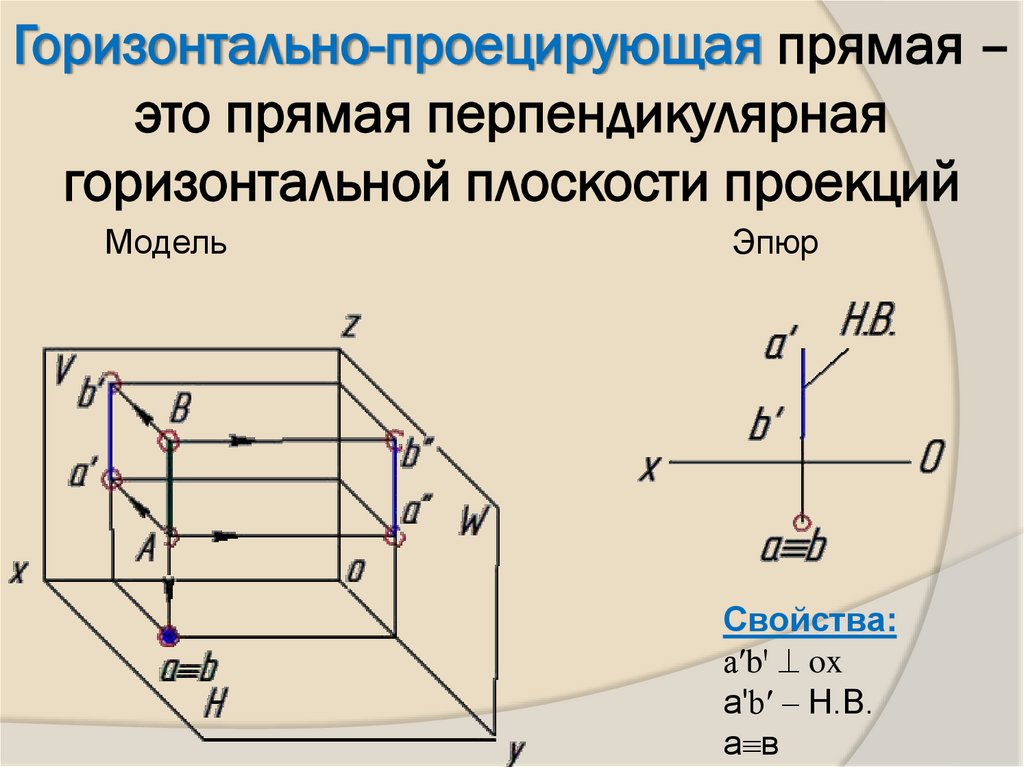
11. Горизонтально-проецирующая прямая – это прямая перпендикулярная горизонтальной плоскости проекций

Модель
Эпюр
Свойства:
аʹbꞌ ox
аʹbʹ – Н.В.
а в

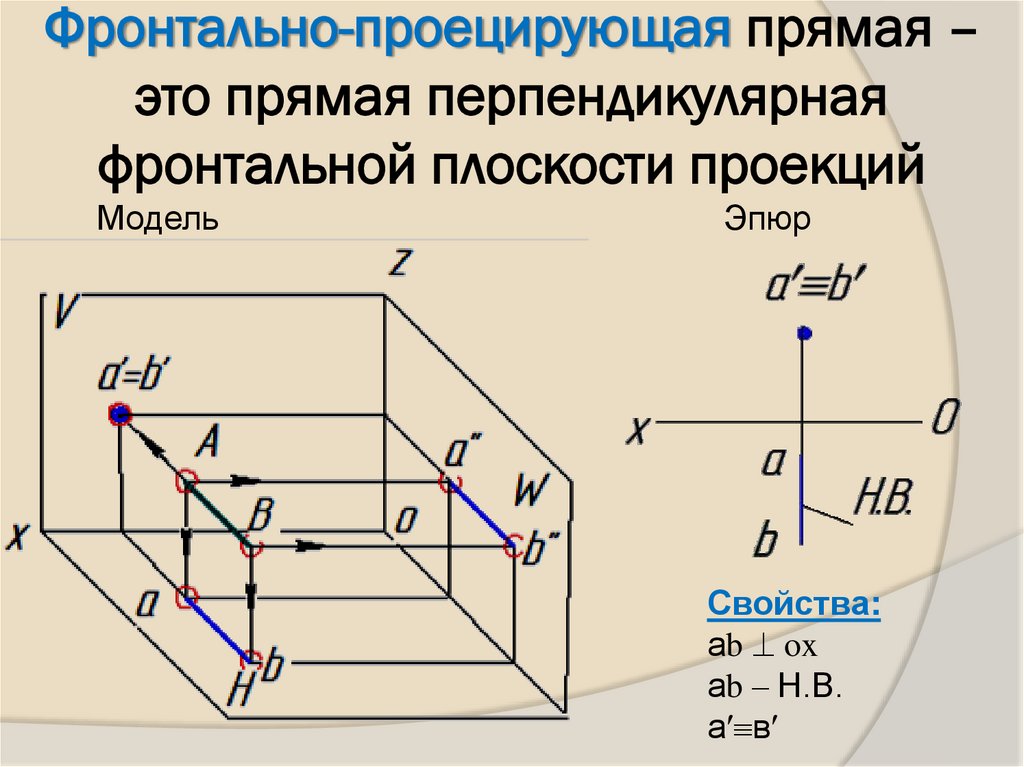
12. Фронтально-проецирующая прямая – это прямая перпендикулярная фронтальной плоскости проекций

Модель
Эпюр
Свойства:
аb ox
аb – Н.В.
аʹ вʹ

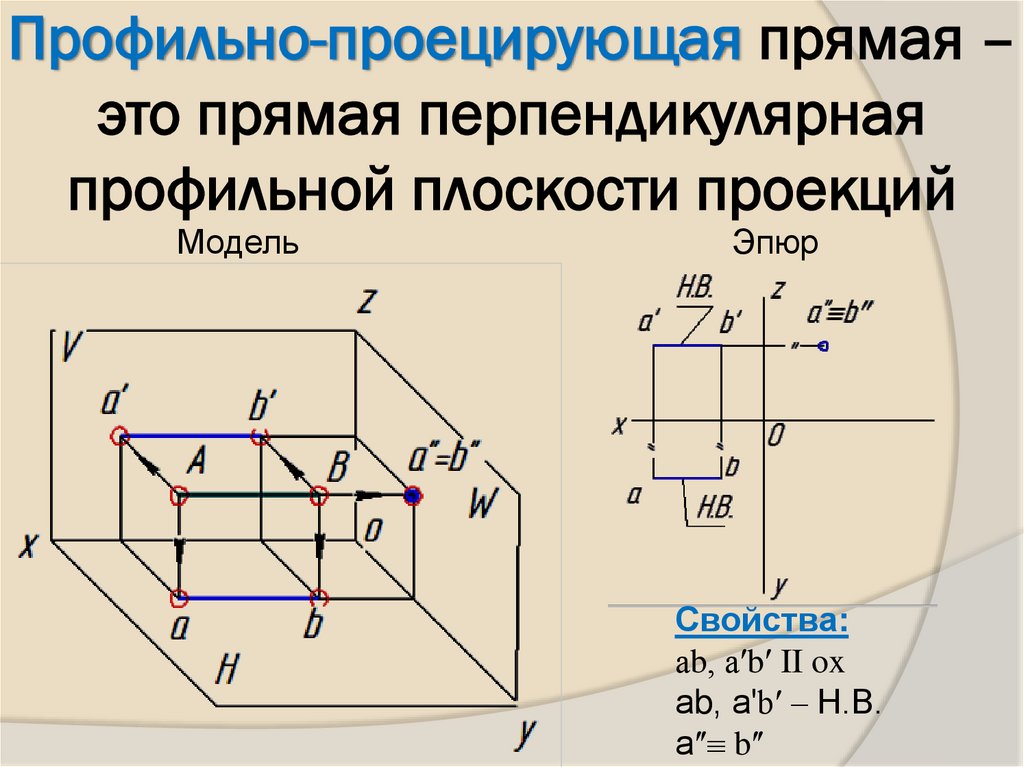
13. Профильно-проецирующая прямая – это прямая перпендикулярная профильной плоскости проекций

Модель
Эпюр
Свойства:
аb, аʹbʹ II ox
аb, аʹbʹ – Н.В.
аʺ bʺ

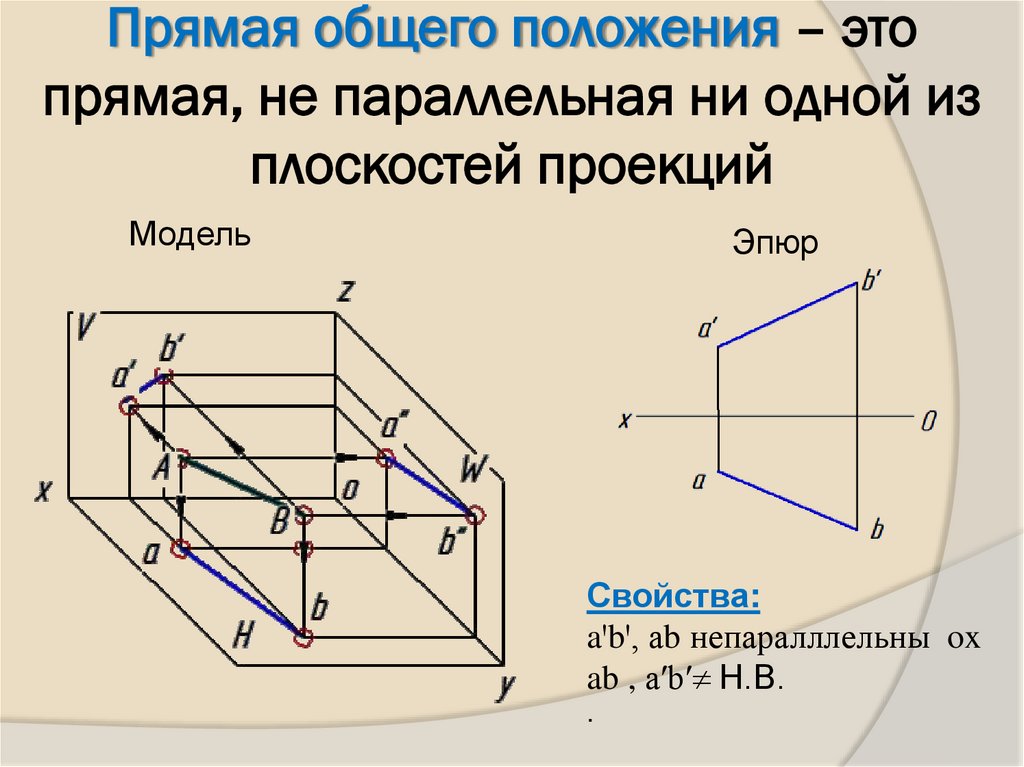
14. Прямая общего положения – это прямая, не параллельная ни одной из плоскостей проекций

Модель
Эпюр
Свойства:
aꞌbꞌ, аb непаралллельны ox
ab , aʹbʹ Н.В.
.

15. Следы прямой

- это точки пересечения прямой с
плоскостями проекций (являются
точками перехода прямой из одной
четверти пространства в другую)

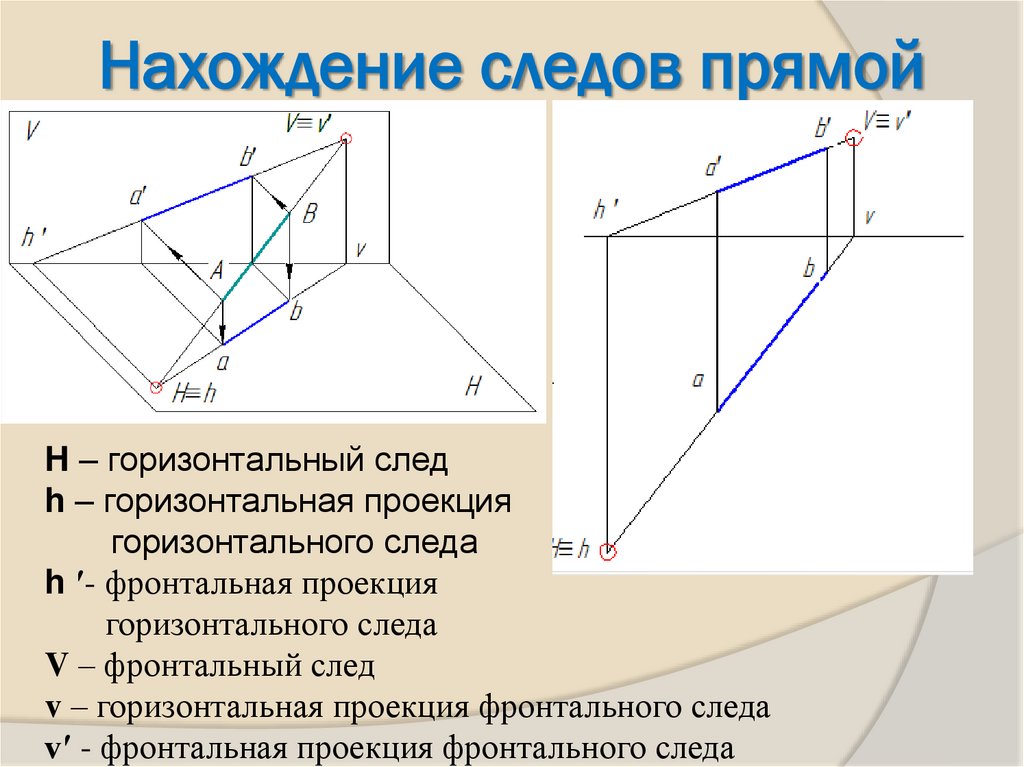
16. Нахождение следов прямой

H – горизонтальный след
h – горизонтальная проекция
горизонтального следа
h ʹ- фронтальная проекция
горизонтального следа
V – фронтальный след
v – горизонтальная проекция фронтального следа
vʹ - фронтальная проекция фронтального следа

17. Вывод

Для построения горизонтального следа прямой
необходимо из точки пересечения фронтальной
проекции прямой с осью OX провести линию
связи до пересечения с продолжением
горизонтальной проекции прямой
Для построения фронтального следа прямой
необходимо из точки пересечения горизонтальной
проекции прямой с осью OX провести линию
связи до пересечения с продолжением
фронтальной проекции

18. Взаимное положение двух прямых

По отношению друг к другу прямые в
пространстве могут быть расположены:
1. параллельно
2. пересекаться
3. скрещиваться

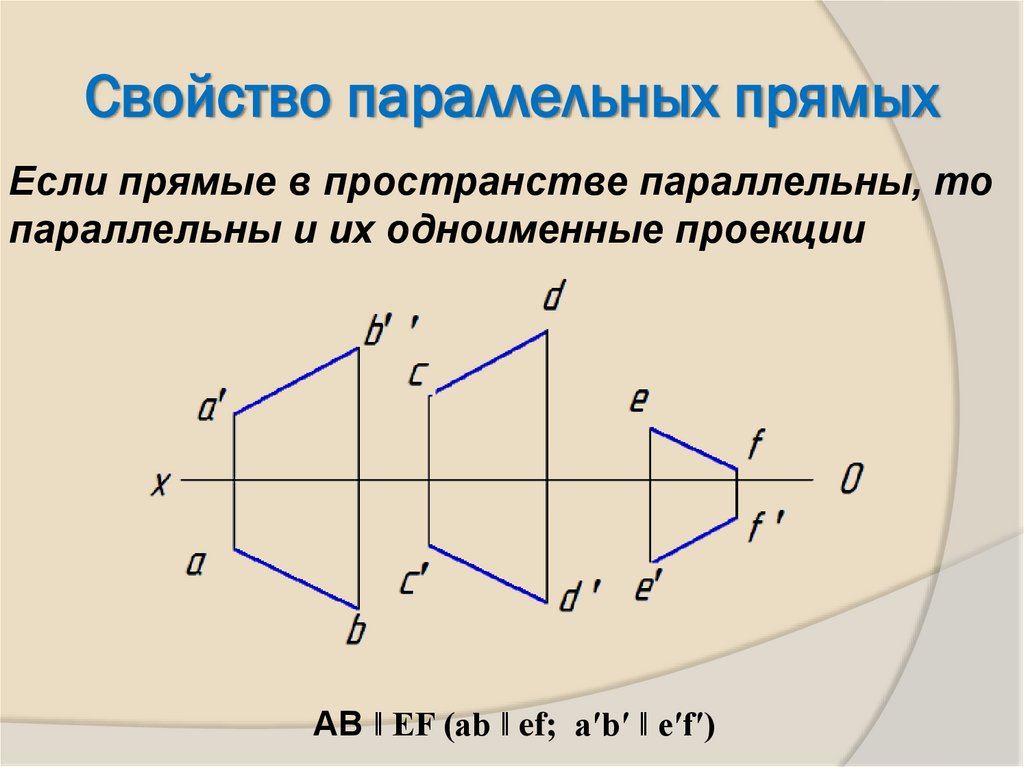
19. Свойство параллельных прямых

Если прямые в пространстве параллельны, то
параллельны и их одноименные проекции
АВ ǁ EF (ab ǁ ef; aʹbʹ ǁ eʹfʹ)

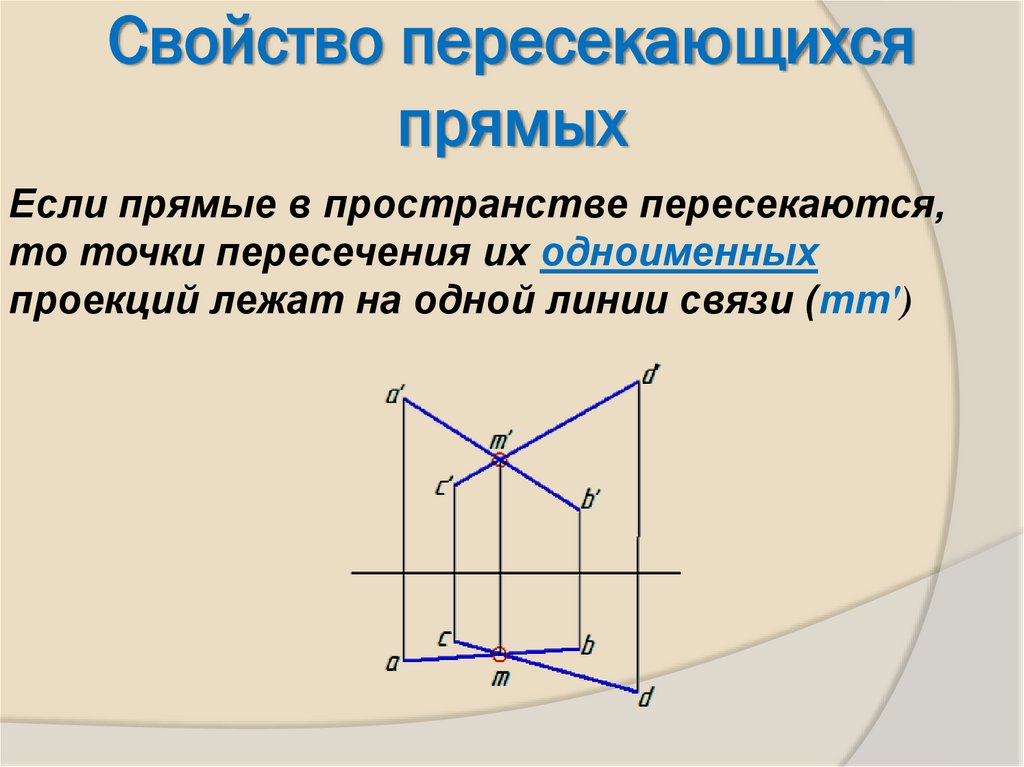
20. Свойство пересекающихся прямых

Если прямые в пространстве пересекаются,
то точки пересечения их одноименных
проекций лежат на одной линии связи (mmʹ)

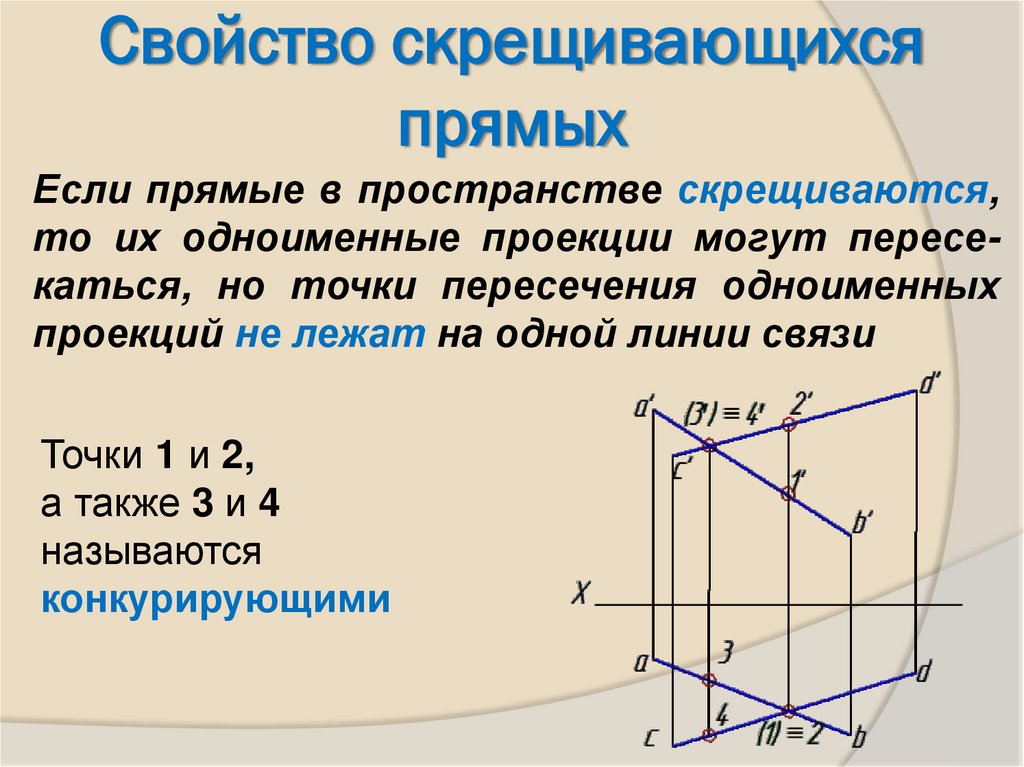
21. Свойство скрещивающихся прямых

Если прямые в пространстве скрещиваются,
то их одноименные проекции могут пересекаться, но точки пересечения одноименных
проекций не лежат на одной линии связи
Точки 1 и 2,
а также 3 и 4
называются
конкурирующими

22. Конкурирующие точки

это точки, проекции которых на какую-либо
плоскость проекций совпадают
Из двух конкурирующих точек видимой будет
та точка, проекция которой расположена
дальше от оси

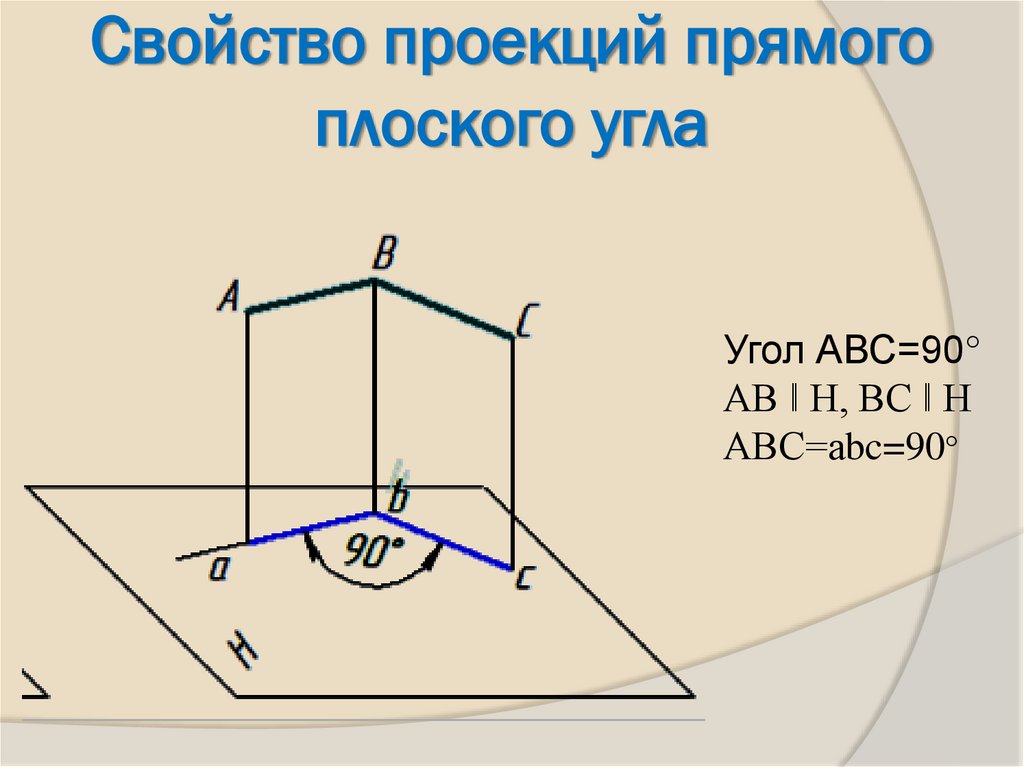
23. Свойство проекций прямого плоского угла

Угол АВС=90°
АВ ǁ Н, ВС ǁ Н
АВС=аbc=90°

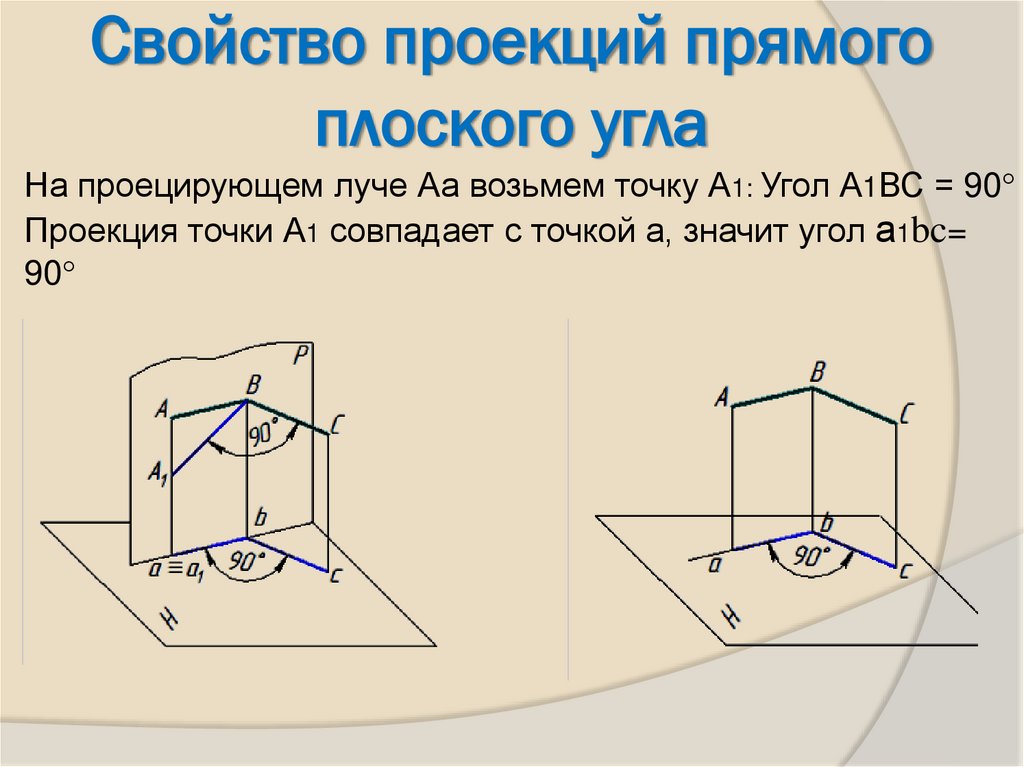
24. Свойство проекций прямого плоского угла

На проецирующем луче Аа возьмем точку А1: Угол А1ВС = 90°
Проекция точки А1 совпадает с точкой а, значит угол а1bc=
90°

25. Свойство проекций прямого плоского угла

Если одна сторона прямого
плоского угла параллельна
плоскости проекций, то прямой
угол на эту плоскость
проецируется в натуральную
величину

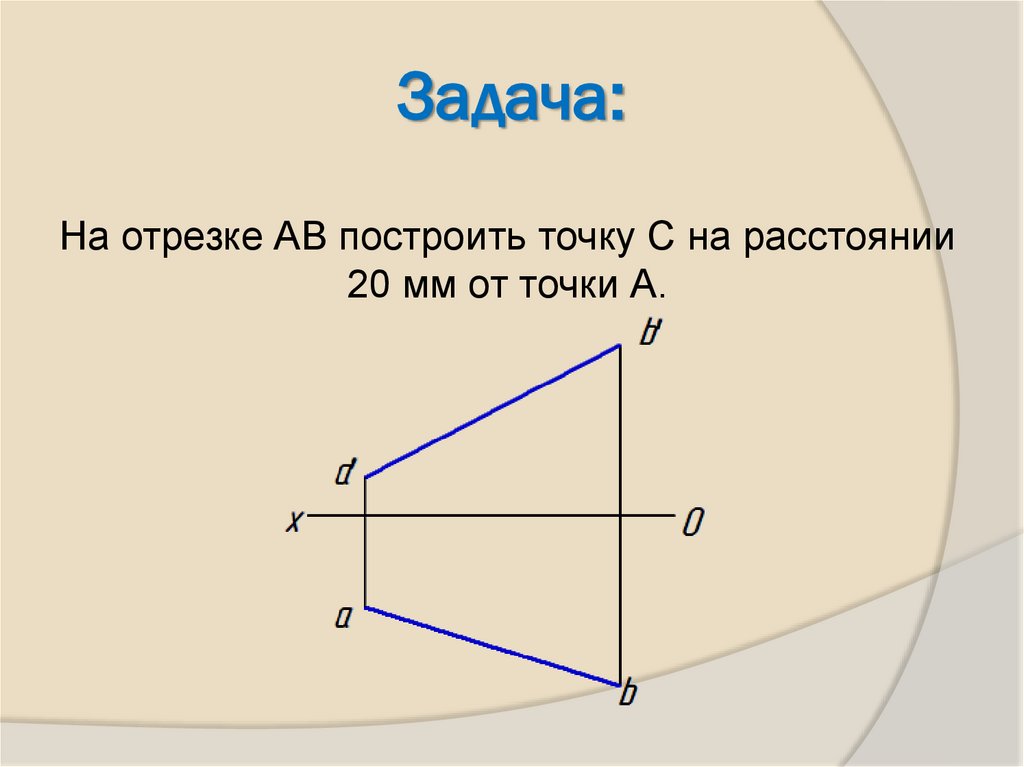
26. Задача:

На отрезке АВ построить точку С на расстоянии
20 мм от точки А.

27.

СПАСИБО ЗА
ВНИМАНИЕ!