Похожие презентации:
Лекция №2 Векторная алгебра (07.10.2025)
1. Векторная алгебра
2.
Скалярное произведение векторовОпр.: Скалярным произведением двух
векторов а и b называется число,
равное произведению длин этих векторов
на косинус угла между ними
a b a b cos
(1)
угол между векторами a и b ,
Обозначение:
a b , a b или a , b
а
b
3.
Свойства скалярного произведения1. Переместительное свойство
а b b а
2. Сочетательное свойство, относительно
скалярного множителя
( а ) b (а b )
3. Распределительное свойство
a (b с ) a b а с
4. Если векторы а и b (ненулевые) взаимно
перпендикулярны, то их скалярное произведение
равно 0.
а b
а b 0
4.
5. Скалярный квадрат вектора равенквадрату его длины
a a а a а cos 0 a
2
2
Следствие: Длина вектора вычисляется по
формуле:
a a а a a a
2
x
2
y
2
z
5.
Пример.Найти длину вектора с 3a 4b , если
a 2, b 3, угол между векторами
Решение :
3a 4b 3a 4b
с с с с 2
3a 4b 9a 24 a b 16 b
2
2
9 4 24 2 3 cos
2
16 9 108 6 3
3 1
2
3
6.
Выражение скалярного произведения черезкоординаты
Заданы 2 вектора
а аx i а y j аz k
b bx i by j bz k
Рассмотрим таблицу скалярных
произведений координатных ортов
i {1,0,0}
j {0,1,0}
k {0,0,1}
i j k
1 0 0
i
j 0 1 0
k 0 0 1
7.
Найдем скалярное произведение векторов а и bа b а x i а y j а z k bx i by j bz k
а x bx i i а x by i j а x bz i k
а y bx j i а y by j j а y bz j k
а z bx k i а z by k j а z bz k k
а x bx 0 0 0 а y by 0 0 0 а z bz
т.е.
а b а x bx а y by а z bz
8.
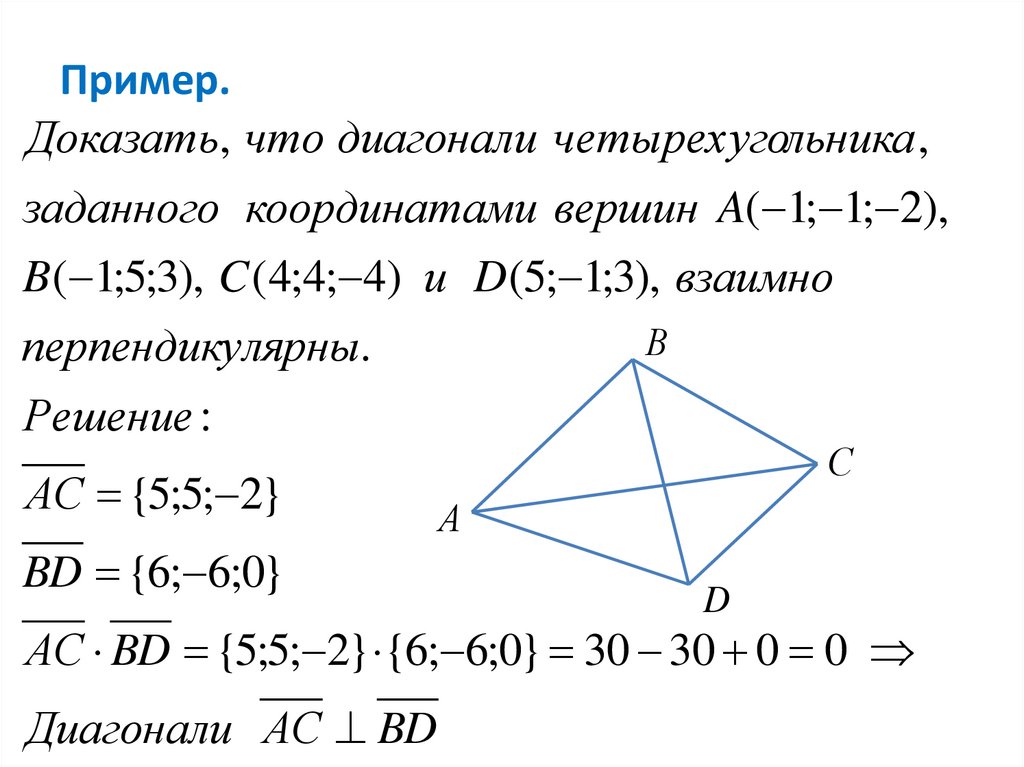
Пример.Доказать, что диагонали четырехугольника ,
заданного координатами вершин A( 1; 1; 2),
B( 1;5;3), C (4;4; 4) и D(5; 1;3), взаимно
перпендикулярны.
Решение :
АС {5;5; 2}
BD {6; 6;0}
В
С
А
D
АС BD {5;5; 2} {6; 6;0} 30 30 0 0
Диагонали АС BD
9.
Приложения скалярного произведения1) Угол между векторами
а аx i а y j аz k
b bx i by j bz k
а b
cos
а b
cos
а x bx а y by а z bz
а x a x а y a y а z a z bx bx by by bz bz
10.
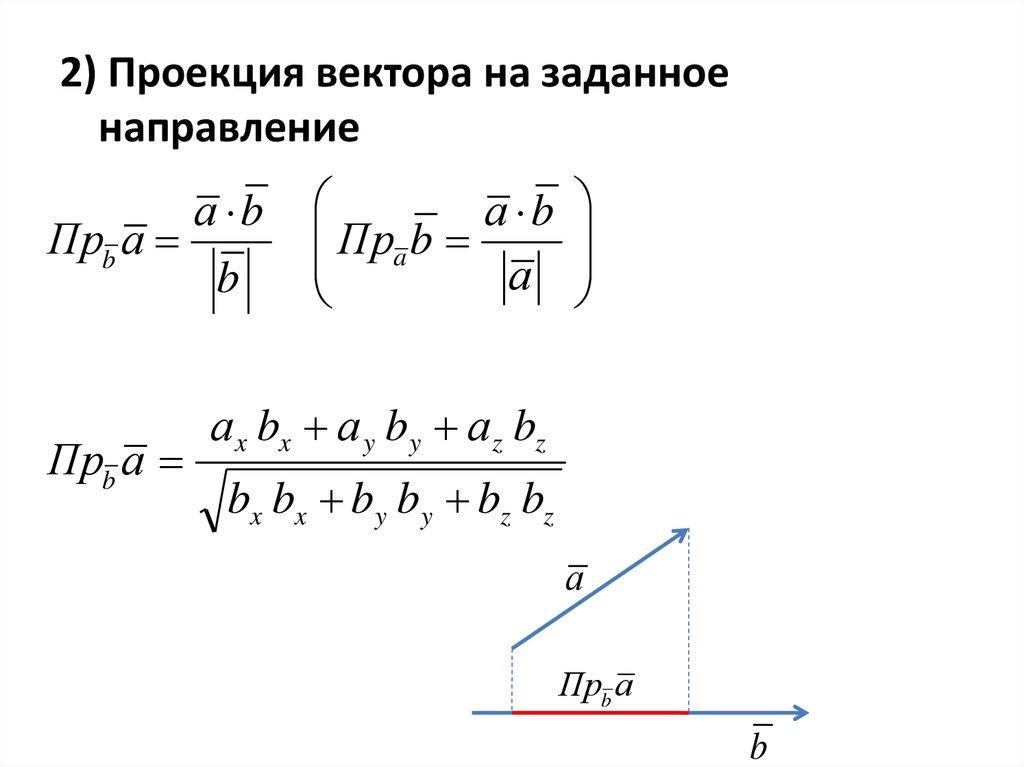
2) Проекция вектора на заданноенаправление
а b
Прb а
b
Прb а
а
b
Прa b
а
а x bx а y by а z bz
bx bx by by bz bz
а
Прb а
b
11.
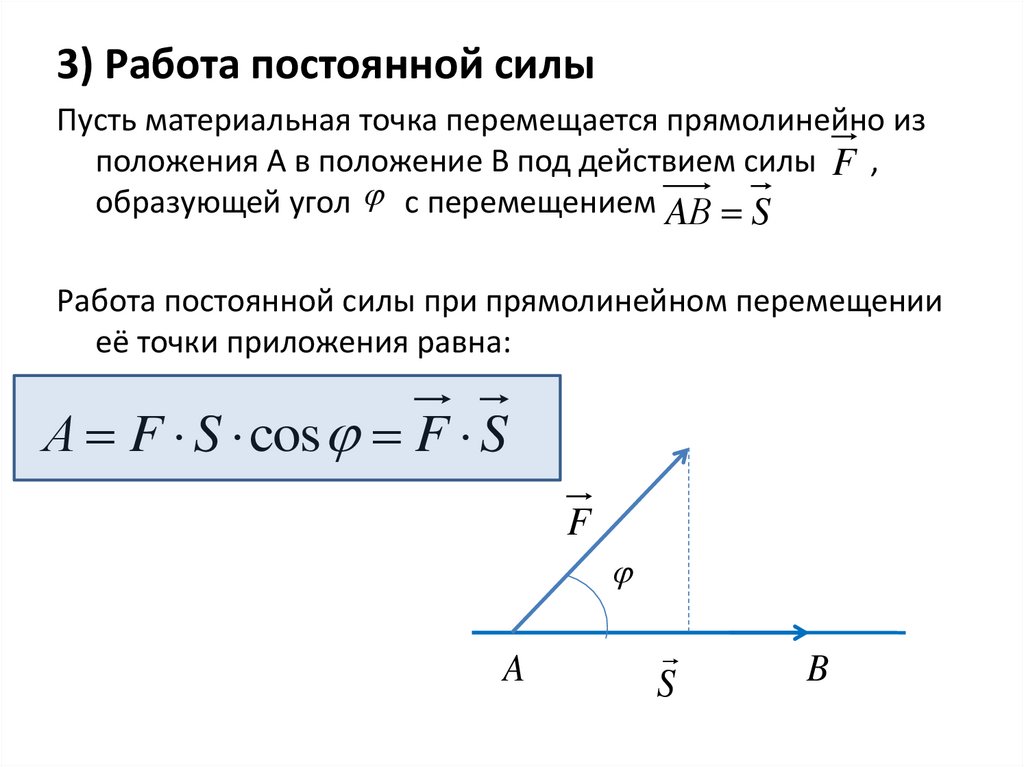
3) Работа постоянной силыПусть материальная точка перемещается прямолинейно из
положения А в положение В под действием силы F ,
образующей угол с перемещением AВ S
Работа постоянной силы при прямолинейном перемещении
её точки приложения равна:
А F S cos F S
F
A
S
B
12.
Пример.Вычислить работу, произведенную силой
F {1;2;4}, если точка её приложения перемещается
прямолиней но из положения А(1;0;2) в положение B (4;1;2).
Под каким углом к АВ напралена сила F ?
Решение :
1) АВ S {4 1;1 0;2 2} {3;1;0}
2) A F S {1;2;4} {3;1;0} 1 3 2 1 4 0 5 (ед. работы)
3) cos
F S
F S
5
1 2 2 4 2 32 12 0
5
21 10
arccos
5
21 10
13.
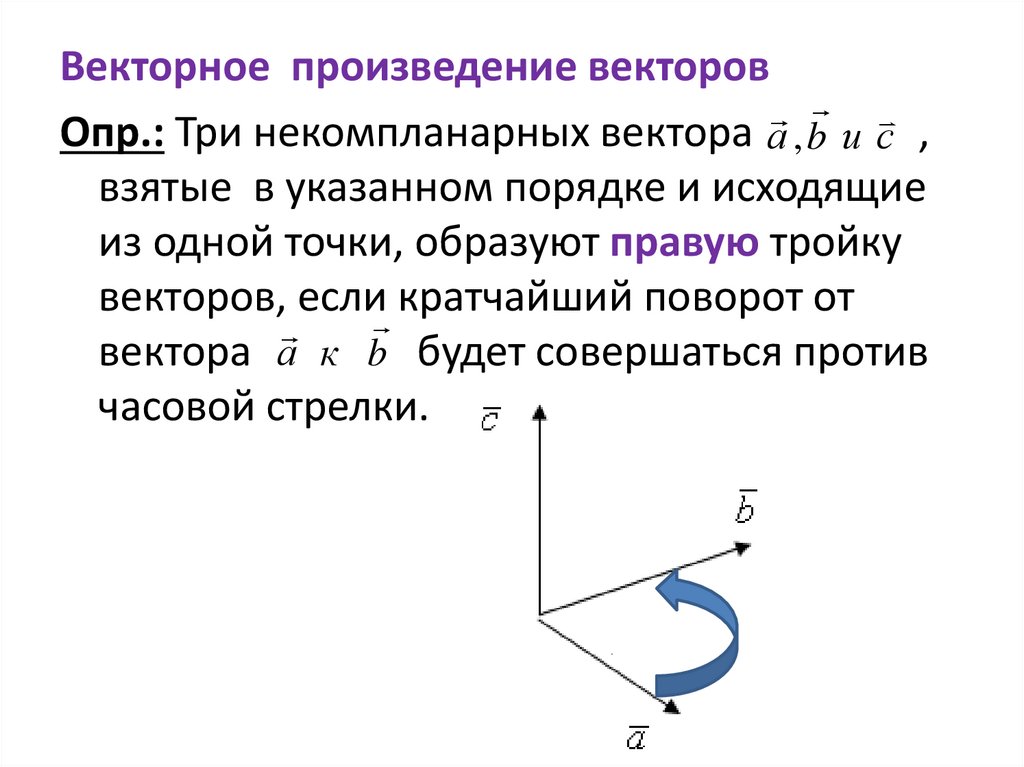
Векторное произведение векторовОпр.: Три некомпланарных вектора а , b и с ,
взятые в указанном порядке и исходящие
из одной точки, образуют правую тройку
векторов, если кратчайший поворот от
вектора а к b будет совершаться против
часовой стрелки.
14.
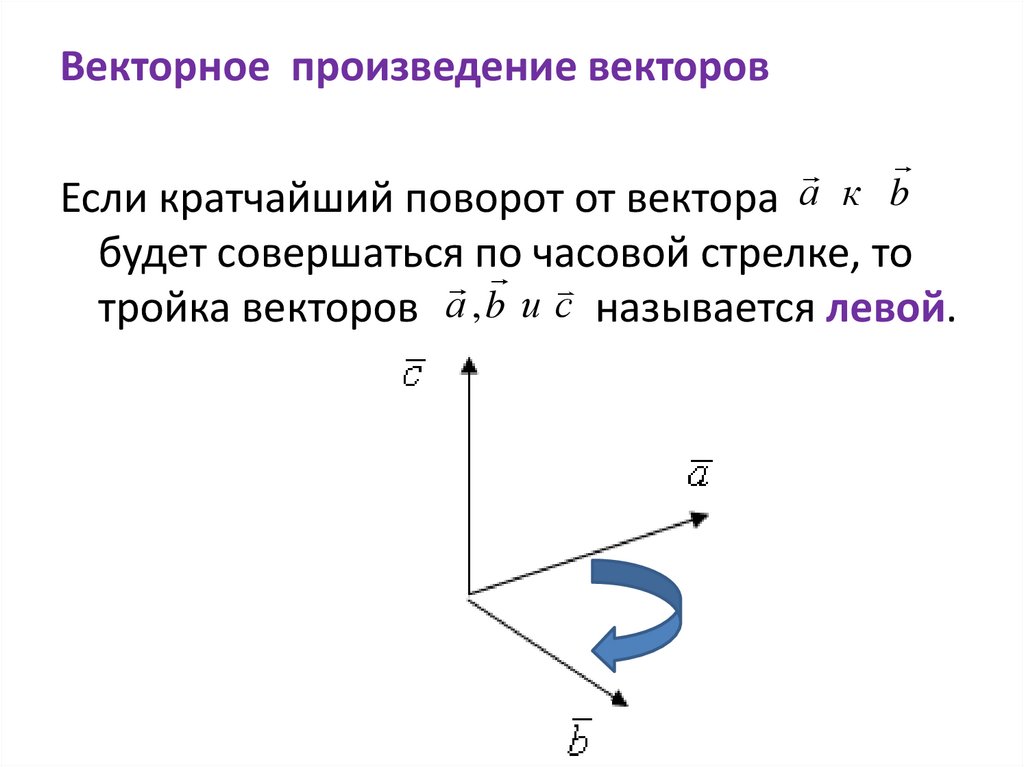
Векторное произведение векторовЕсли кратчайший поворот от вектора а к b
будет совершаться по
часовой стрелке, то
тройка векторов а , b и с называется левой.
15.
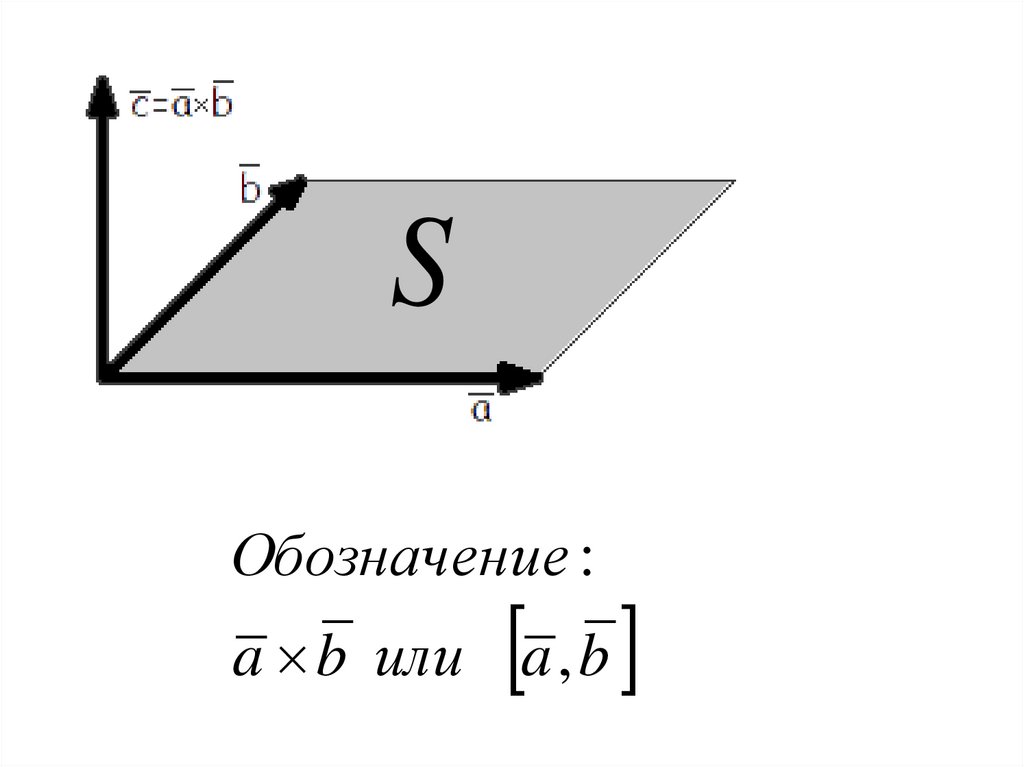
Векторное произведение векторовОпр.: Векторным произведением двух векторов
а и b называется вектор с , который:
1) перпендикулярен векторам a и b , т.е.
с а и с b
2) имеет длину, численно равную площади
параллелограмма , построенного на векторах
a и b , которая вычисляется по формуле :
с a b a b sin
угол между векторами a и b
3) векторы a , b и с образуют правую тройку векторов
16.
SОбозначение :
a b или a , b
17.
Свойства векторного произведения1. При перестановке сомножителей векторное
произведение меняет знак
а b b а
2. Сочетательное свойство, относительно скалярного
множителя
а b (а ) b а ( b )
3. Распределительное свойство
( a b ) с a с b c
4. Если векторы а и b (ненулевые) коллинеарны, то
их векторное произведение равно нулевому вектору.
а | |b а b 0
18.
Выражение векторного произведения черезкоординаты
а аx i а y j аz k
b bx i by j bz k
ay
by
az
i
j
k
a b ax
bx
ay
by
az
bz
ax
az
j
bx
bz
ау
ax
i
bz
bx
by
k.
19.
Пример. Найдите векторное произведениевекторов
a 2; 3; 1
b 3; 1; 2
20.
Решение :i
j k
с a b 2 3 1
3 1 2
3 1
2 1
2 3
i
j
k
1 2
3 2
3 1
( 6 1)i (4 3) j (2 9)k
7i 7 j 7k
с a b { 7, 7, 7}
21.
Приложения векторного произведения1) Угол между векторами
а аx i а y j аz k
b bx i by j bz k
sin
а b
а b
22.
2) Проверка векторов на коллинеарностьi
a b ax
bx
j
ay
by
k
az 0
bz
ax a y az
a||b
bx by bz
23.
3) Нахождение площади параллелограмма итреугольника
S пар. a b a b sin
1
S a b
2
24.
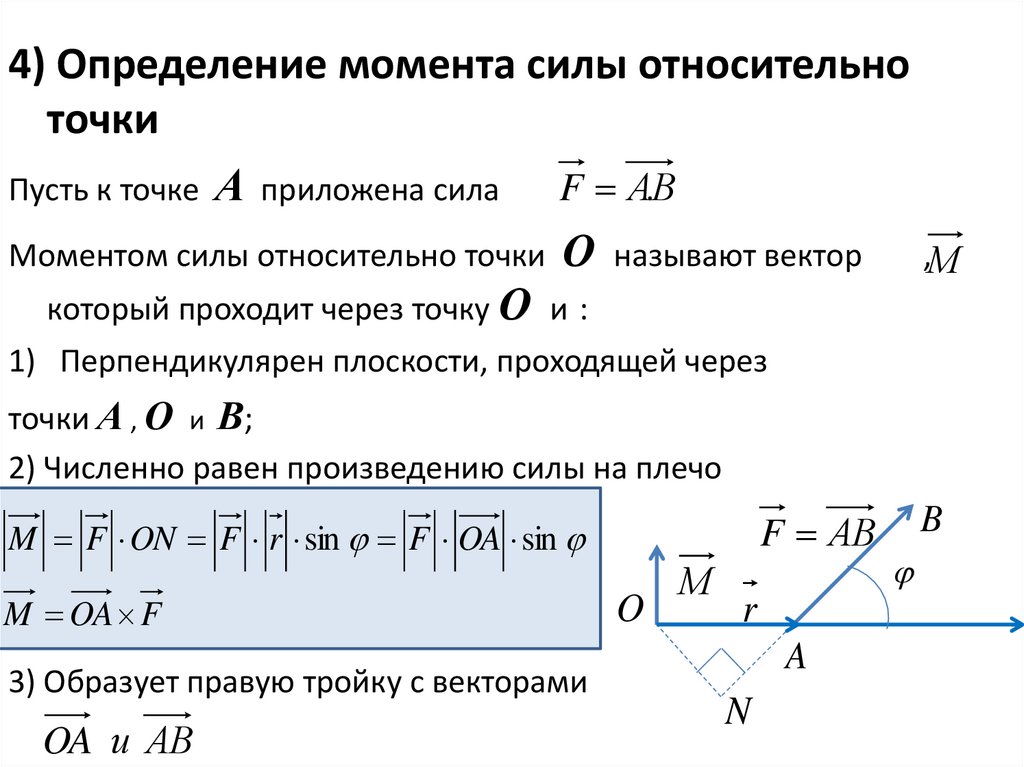
4) Определение момента силы относительноточки
Пусть к точке А приложена сила
.
F АВ
Моментом силы относительно точки О называют вектор
,М
который проходит через точку О и :
1) Перпендикулярен плоскости, проходящей через
точки А , О и В;
2) Численно равен произведению силы на плечо
F АВ
M F ON F r sin F OA sin
M OA F
3) Образует правую тройку с векторами
OA и АВ
O
М
r
A
N
B
25.
Пример. Вычислите площадь треугольникаАВС, построенного на векторах
AB 3; 5; 0
AC 1; 1; 2
26.
Решение :1
S ABC AB AC .
2
i
AB AC 3
j
5
k
0 10i 6 j 8k .
1 1 2
27.
1S ABC AB AC
2
1
2
2
2
10 ( 6) ( 8)
2
1
1
200 10 2 5 2 ( кв. ед)
2
2
28.
Смешанное произведение векторовОпр.: Смешанным произведением
упорядоченной тройки векторов а, b и с
называется число, равное скалярному
произведению вектора а b на с , т.е.
a b с
Обозначение:
a b с , a b с или a b с
29.
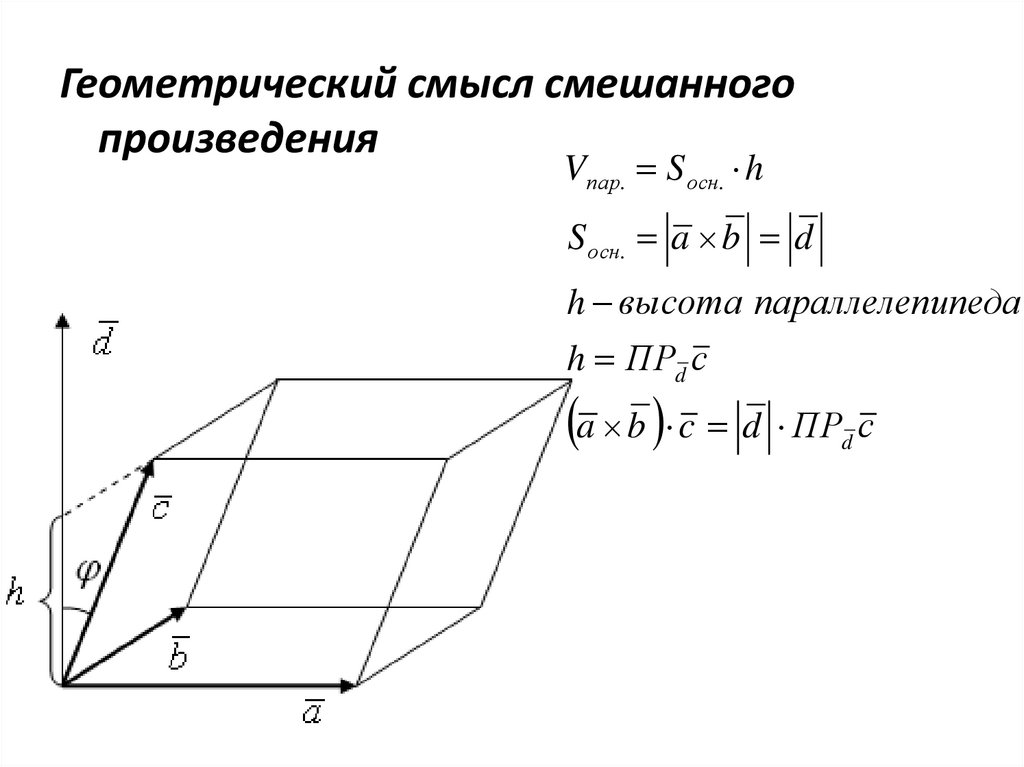
Геометрический смысл смешанногопроизведения
Vпар. S осн. h
S осн. a b d
h высота параллелепипеда
h ПРd с
a b c d ПР с
d
30.
Свойства смешанного произведения1. При циклической перестановке сомножителей
смешанное произведение не меняется
а b с b с а с а b
2. Смешанное произведение не меняется при перемене
местами знаков векторного и скалярного умножения
а b с а b c
3. Смешанное произведение меняет свой знак при
перемене мест любых двух векторов-сомножителей
a b с a c b b a c c b a
4. Смешанное произведение ненулевых векторов равно
нулю тогда и только тогда, когда они компланарны.
31.
Выражение смешанного произведениячерез координаты
а аx i а y j аz k
b bx i by j bz k
с сx i с y j сz k
ax
ay
az
a b с bx
сx
by
сy
bz
сz
32.
Приложения смешанного произведения1) Проверка тройки векторов на
компланарность
ax
a b с bx
сx
ay
by
сy
az
bz 0
сz
a b с 0 тройка векторов a , b , с правая
a b с 0 тройка векторов a , b , с левая
33.
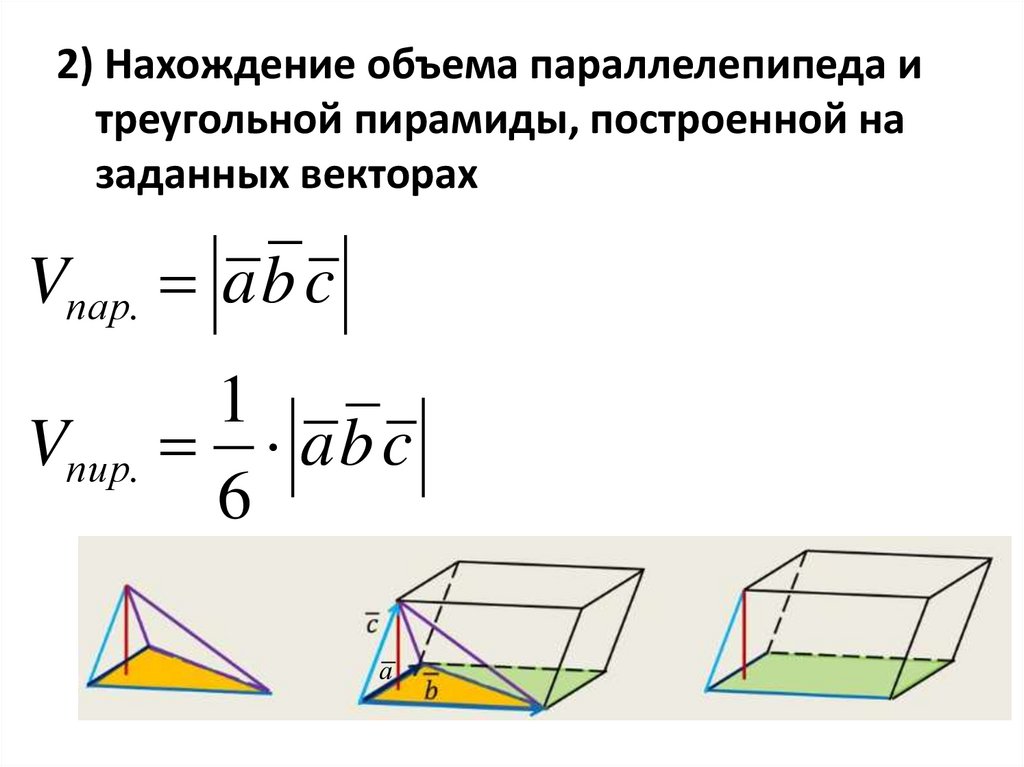
2) Нахождение объема параллелепипеда итреугольной пирамиды, построенной на
заданных векторах
Vпар. a b c
1
Vпир. a b c
6
а
34.
Пример. Найдите объём пирамиды,построенной на векторах
a 3i 4 j k
b 2i j k
c
c i 2 j 5k
b
а
35.
Решение :x1
a b c x2
x3
y1
y2
y3
z1
z2
z3
3 4 1
2 1 1 3 3 4 11 5 1 48
1 2 5
48
Vпир
8 ( куб . ед.)
6
36.
Пример. Установите, компланарны ливекторы
a 3i 5 j
b i j 2k
c 5i 3 j 4k
37.
Решение :Проверим условие компланарности
a b c 0
3 5 0
a b c 1 1 2 3 ( 10) 5 ( 6) 0
5 3 4
Векторы a , b , c компланарны.













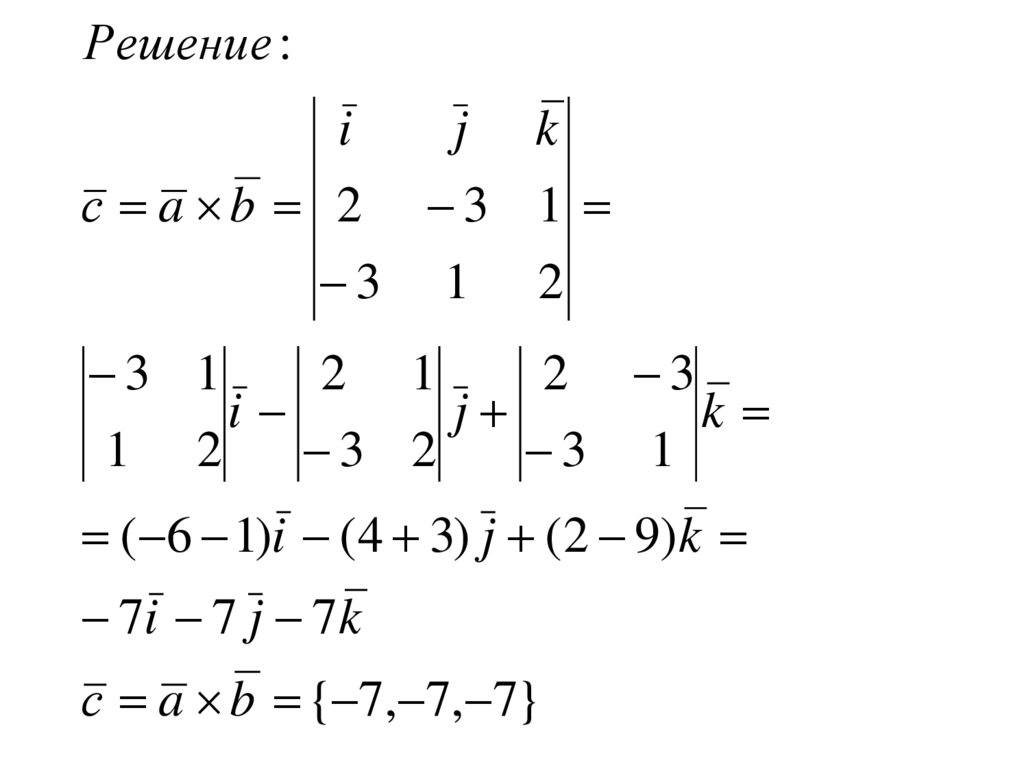




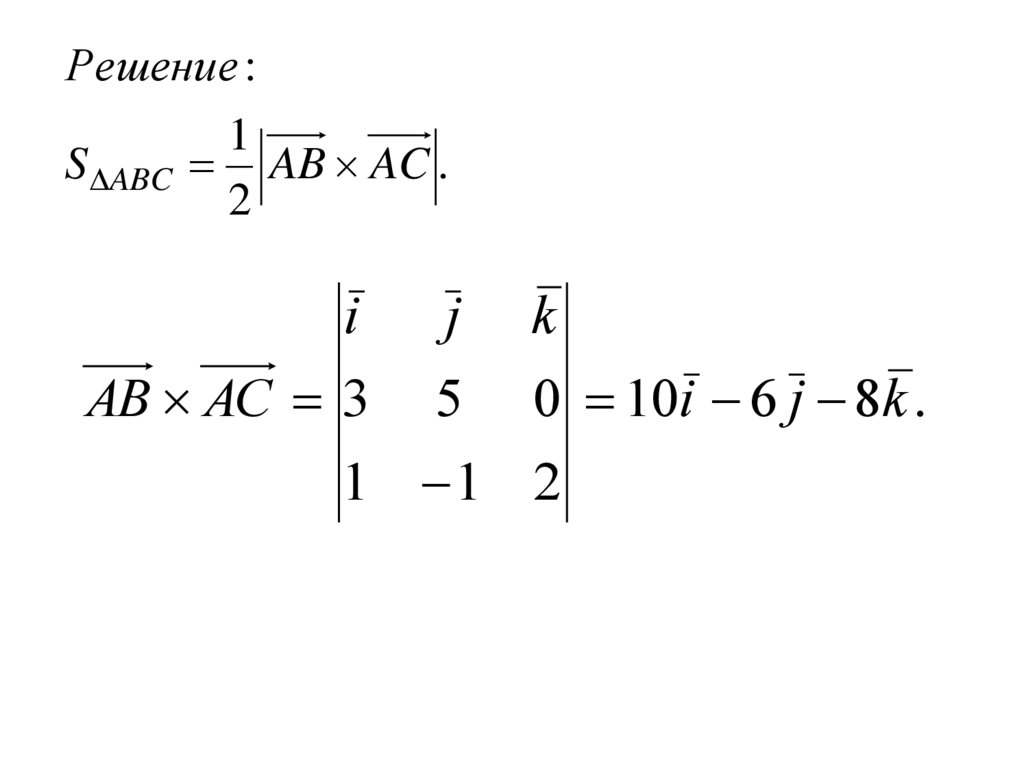
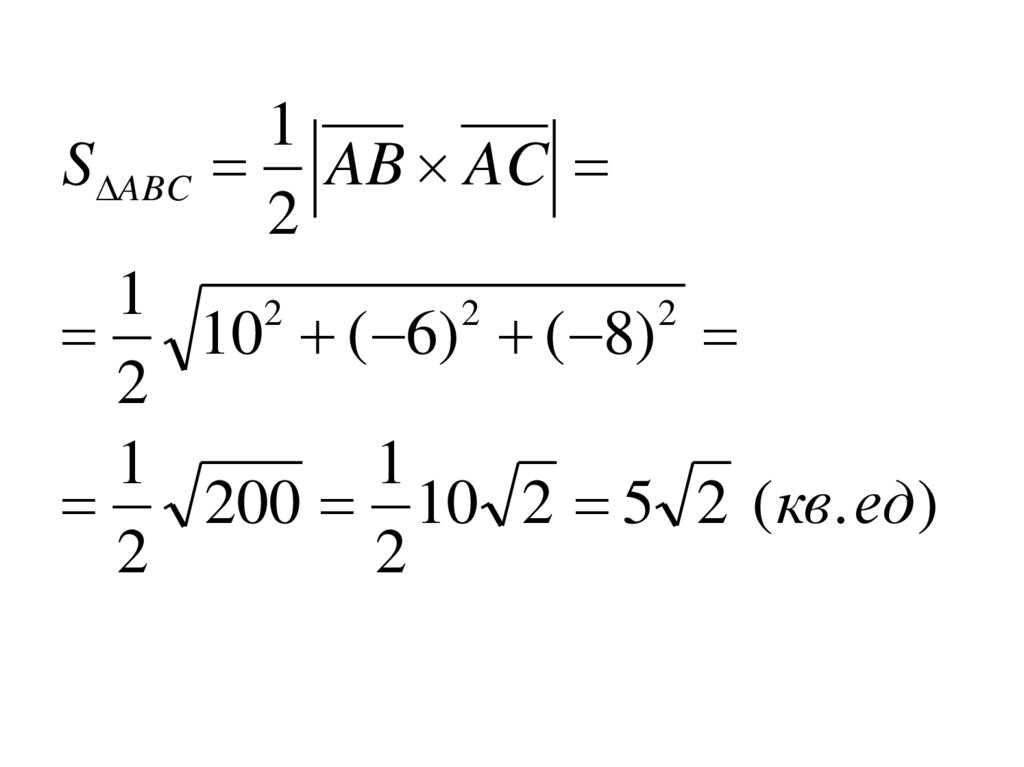





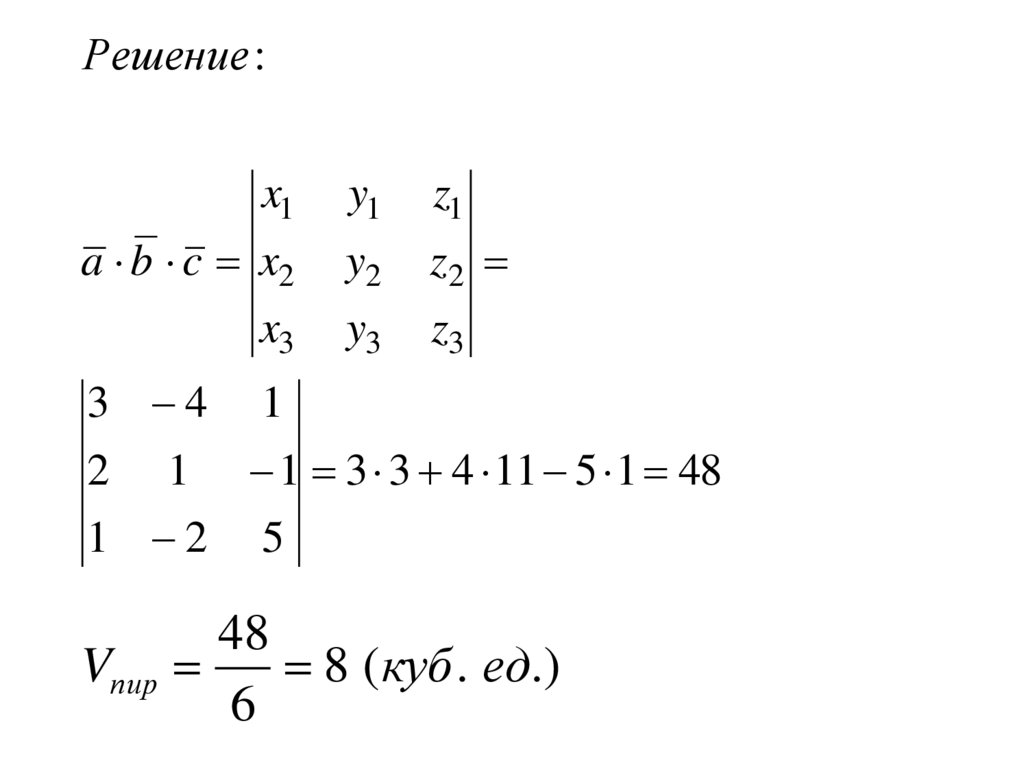



 Математика
Математика








