Похожие презентации:
Дифференциальные уравнения
1. Дифференциальные уравнения
Линейные неоднородные дифференциальныеуравнения второго порядка с постоянными
коэффициентами
2.
• Линейные неоднородныедифференциальные уравнения второго
порядка с постоянными коэффициентами
имеют вид: y py qy f (x)
• Решение этих уравнений основано на
следующей теории.
Th: Общее решение линейного
неоднородного дифференциального
уравнения выражается суммой
его
частного решения и общего
решения соответствующего
линейного однородного уравнения.
y y * Y
3.
Пусть имеем уравнениеq – действительные числа.
(1), где p,
Характеристическое уравнение:
Рассмотрим случаи:
1.
Правая часть уравнения (1) имеет вид:
,
где
случаи:
- многочлен n—ой степени. Тогда возможны
А) число не является корнем характеристического
уравнения. Тогда частное решение нужно искать в виде:
4.
Б) число является однократным корнемхарактеристического уравнения. Тогда частное решение
нужно искать в виде:
В) число является двукратным корнем
характеристического уравнения. Тогда частное решение
нужно искать в виде:
5.
2. Правая часть уравнения (1) имеет вид:,
где
случаи:
– многочлены. Тогда возможны
А) число
не является корнем характеристического
уравнения. Тогда частное решение нужно искать в виде:
,
где
- многочлены, степень которых равна
наивысшей степени многочленов
и
.
6.
является корнем характеристическогоБ) число
уравнения. Тогда частное решение нужно искать в виде:
,
- многочлены, степень которых равна
где
.
и
наивысшей степени многочленов
.
7.
3. Правая часть уравнения (1) имеет вид:,
где где
случаи:
– постоянные числа. Тогда возможны
В) число не является корнем характеристического
уравнения. Тогда частное решение нужно искать в виде:
,
где
– постоянные числа.
Г) число является корнем характеристического
уравнения. Тогда частное решение нужно искать в виде:
),
где
– постоянные числа.
8.
ПР. у" - 2у' - 3у = 2хнач. усл.:
у(0) = 0
у'(0) = 1
у* = Ах + В
у*' = А; у*" = 0
-2А — 2Ах — 3В = 2х
A 1
2 A 2
A 1
;
2
2 A 3B 0 3B 2 B
3
2
y* x
3
9.
k2 — 2k — 3 = 0D = 4 + 12 = 16
2 4
k1
3
2
k2 = -1
Y = C1 e-x + C2 e3x
2
y C1e C2 e x
3
x
3x
y' = -C1e-x + 3C2e3x — 1
10.
22
C1 C2
C
C
0
1
3
2
;
3
4
C1 3C2 1 1 4C2 2
3
1
1
C2 3
C2
3
C 2 1 C1 1
1
3 3
y e
x
1 3x
2
e x
3
3
11.
ПР. y" – 2y' = 24xk2 – 2k = 0
q=0
k (k – 2) = 0
у* = Ах2 + Вх
k = 0, k = 2
y*' = 2Ах + В
Y = C1 + C2e2x
y*" = 2А
2А — 4Ax — 2В = 24х
4 A 24 A 6 A 6
2 A 2 B 0 A B B 6
у* = -6х2 – 6х
y = -6x2 – 6x + C1 + C2e2x
12.
ПР. y" – 3y' – 4y = 9e2xk2 – 3k – 4 = 0
D = 9 + 16 + 25
3 5
k1
4
2
k2 = -1
Y = C1e-x + C2e4x
y* = Ae2x
y*' = 2Ae2x
y*" = 4Ae2x
13.
4Ae2x – 6Ae2x – 4Ae2x = 9e2x-6A = 9
9
1
A 1
6
2
1 2x
x
4x
y 1 e C1e C 2 e
2







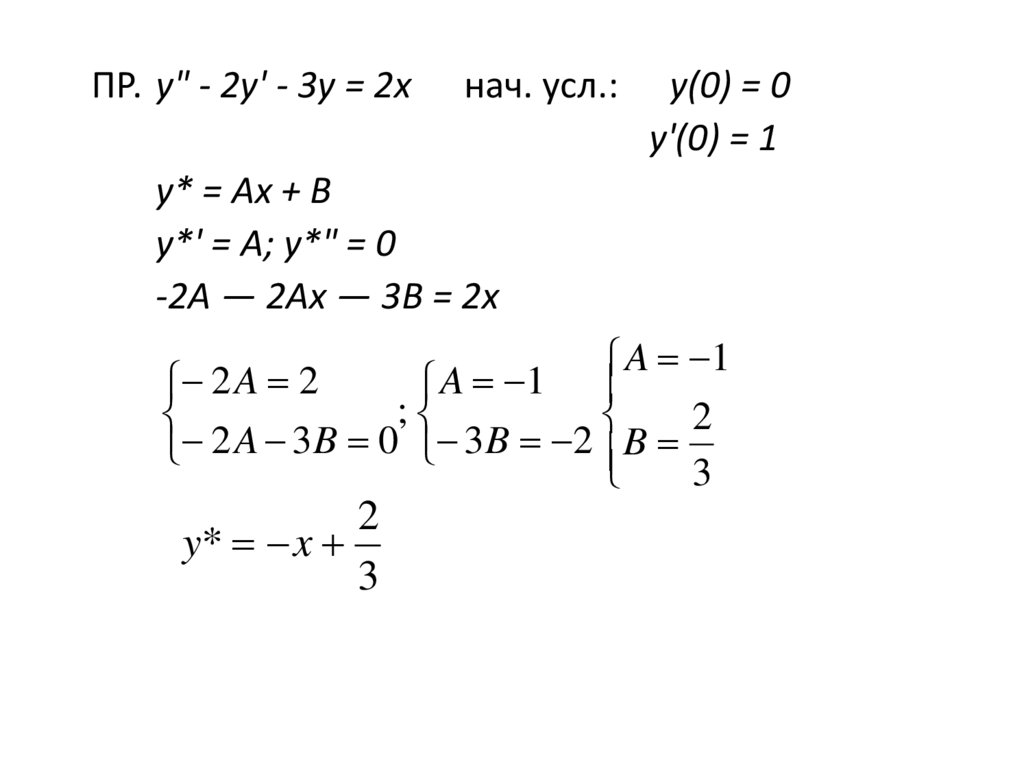
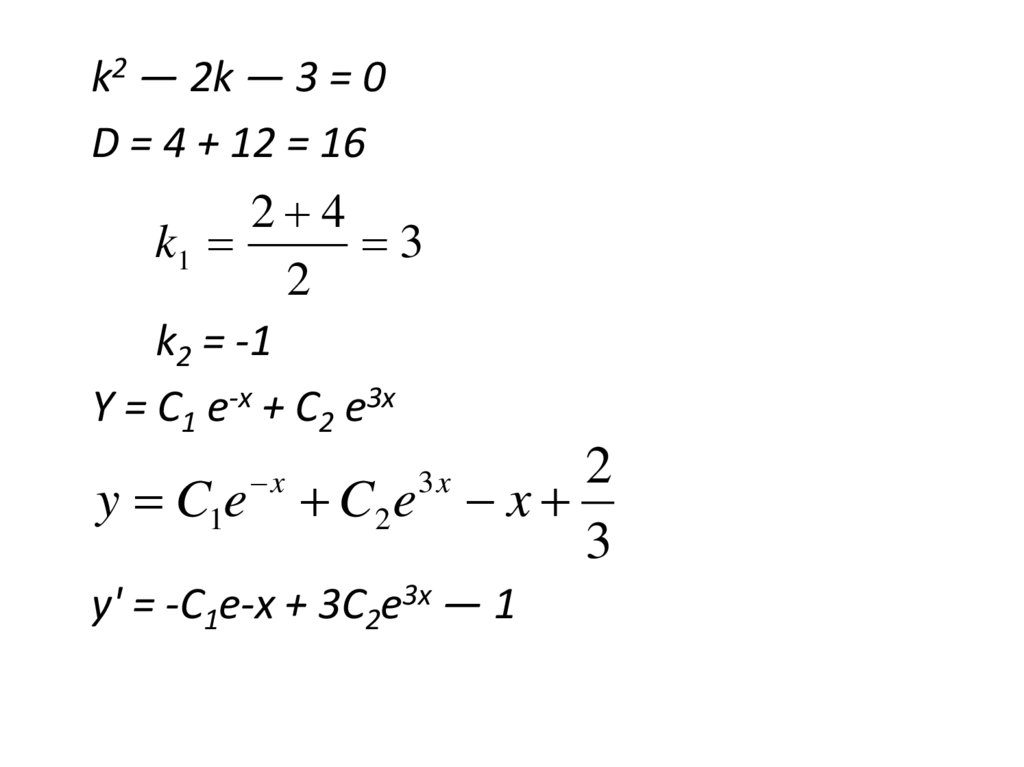
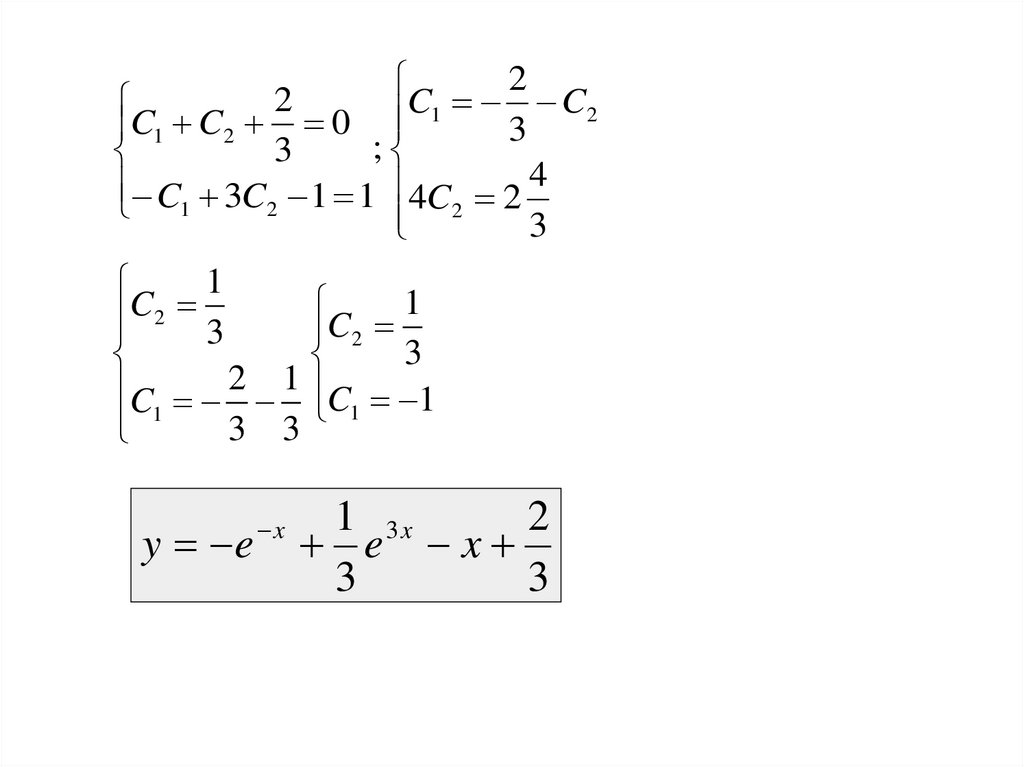
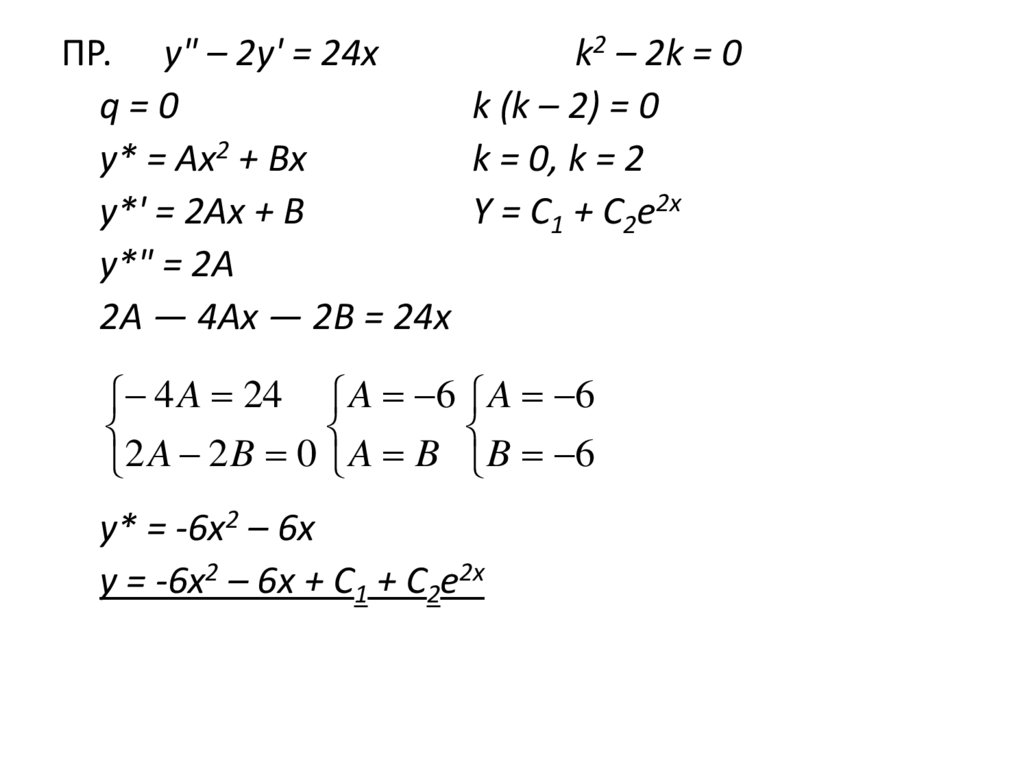
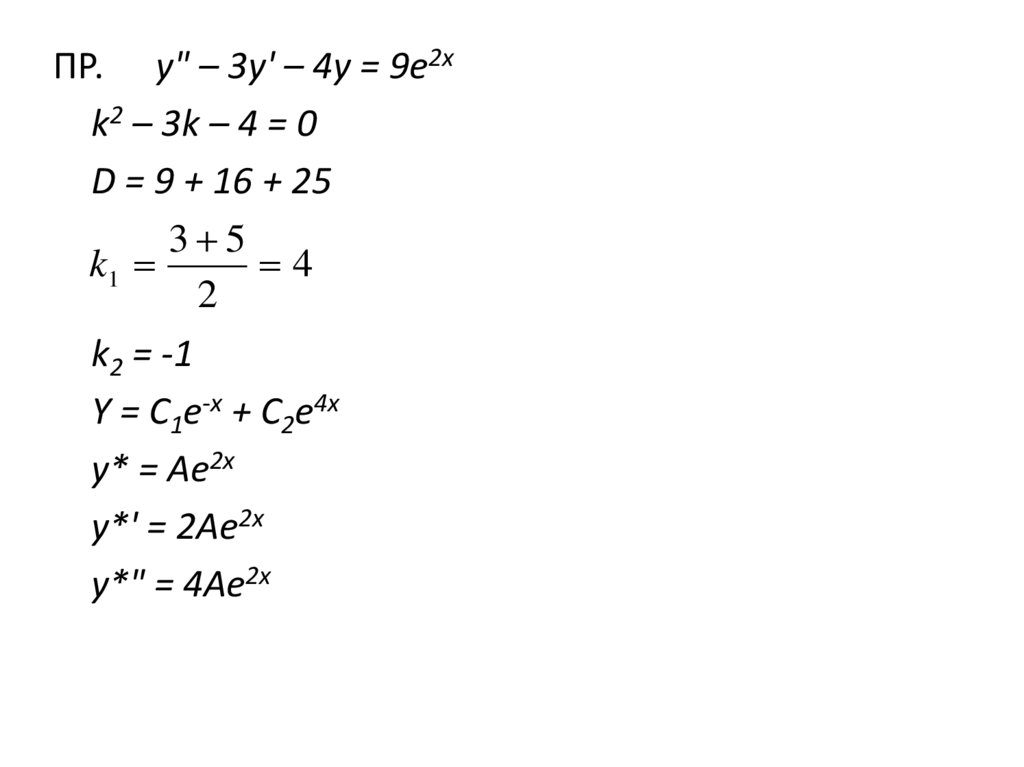
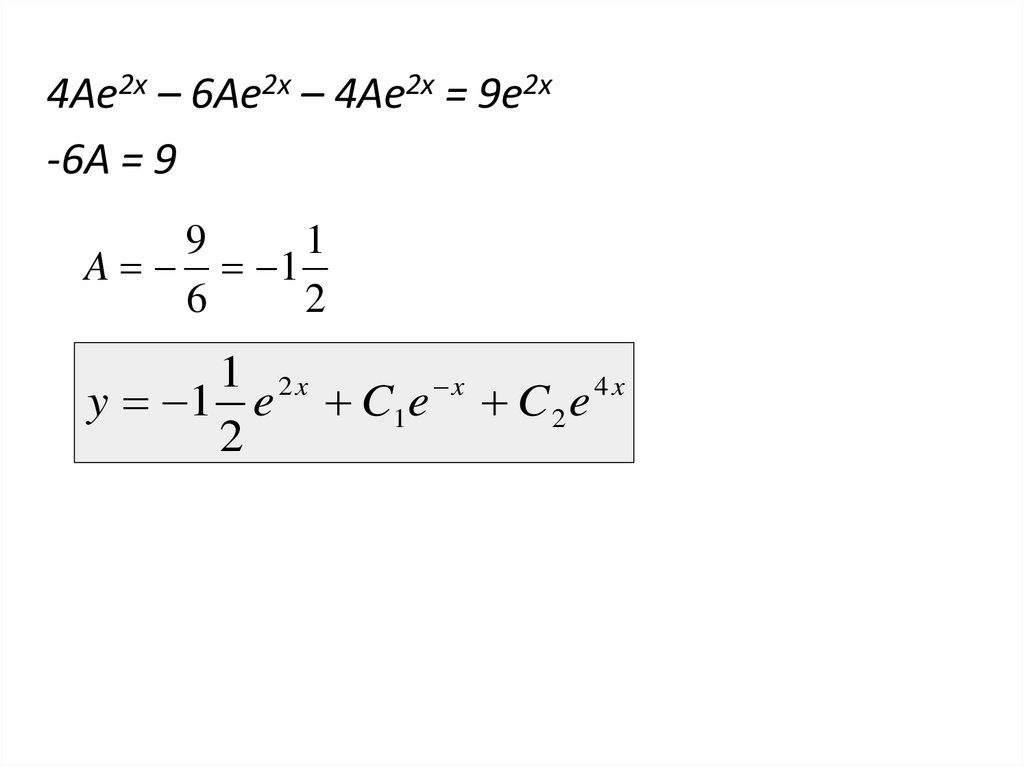
 Математика
Математика








