ege_pryamougolnyy_parallelepiped

1.

2.

Стереометрия

3.

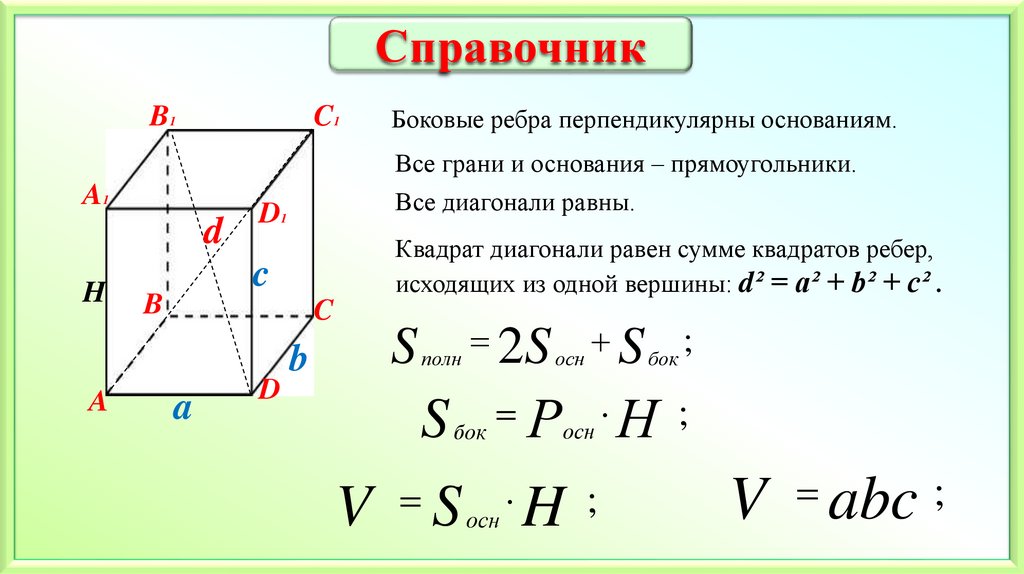
Справочник
B1
C1
A1
d
H
A
Все грани и основания – прямоугольники.
Все диагонали равны.
D1
Квадрат диагонали равен сумме квадратов ребер,
исходящих из одной вершины: d² = a² + b² + c² .
c
B
Боковые ребра перпендикулярны основаниям.
C
a
D
S
b
полн
S
V
2S осн S бок ;
;
Р
Н
осн
бок
S осн H ;
V abc ;

4.

№1
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите
третье ребро параллелепипеда, выходящее из той же вершины.
Решение:
S полн 2S осн S бок 94
2 S осн 2 3 4 24
S бок S полн 2 S осн 94 – 24 = 70
B1
A1
D1
?
B
S бок Pосн H ; Pосн 2(4 3) 14
14 H 70; H
C1
C
3
A
D
4
3
5
3
10 х
х

5.

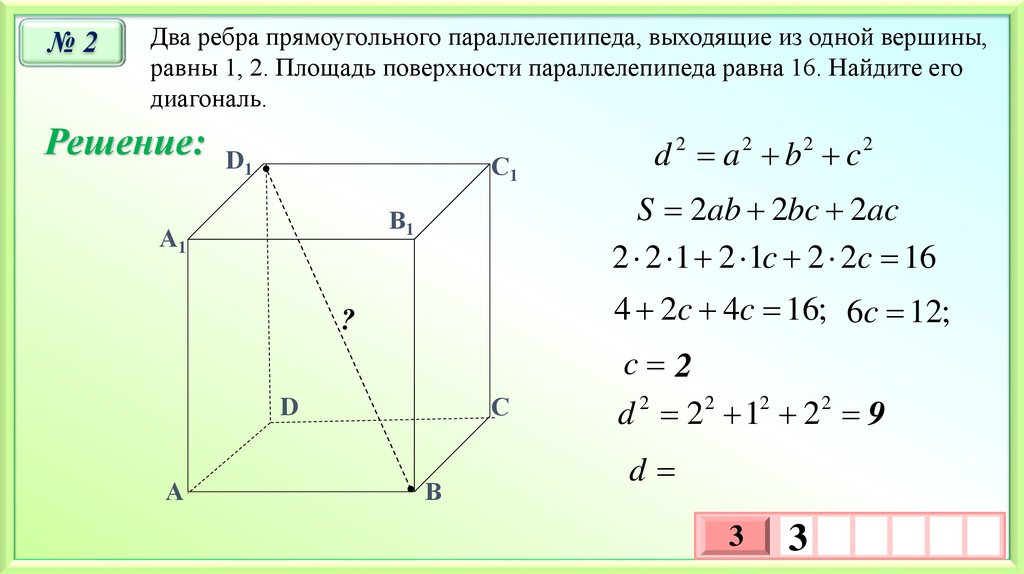
№2
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его
диагональ.
Решение: D
С1
1
2
2
2
S 2ab 2bc 2ac
2 2 1 2 1c 2 2c 16
В1
А1
d a b c
2
4 2c 4c 16; 6c 12;
?
c 2
С
D
А
В
d 2 2 2 12 2 2 9
d
3
3
3
10 х
х

6.

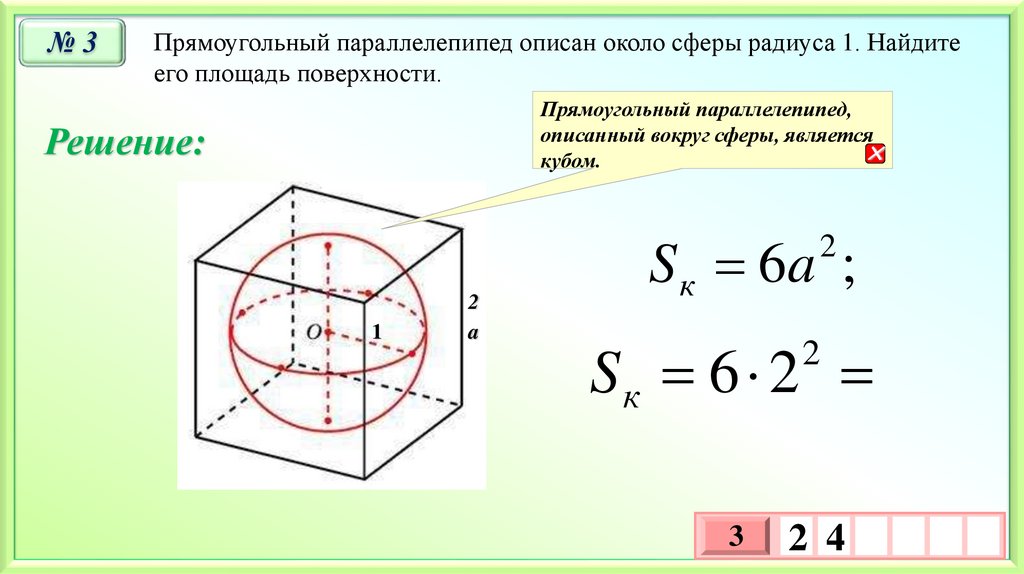
№3
Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите
его площадь поверхности.
Прямоугольный параллелепипед,
описанный вокруг сферы, является
кубом.
Решение:
S к 6a ;
2
1
2
a
Sк 6 2
2
3
2 4
3
10 х
х

7.

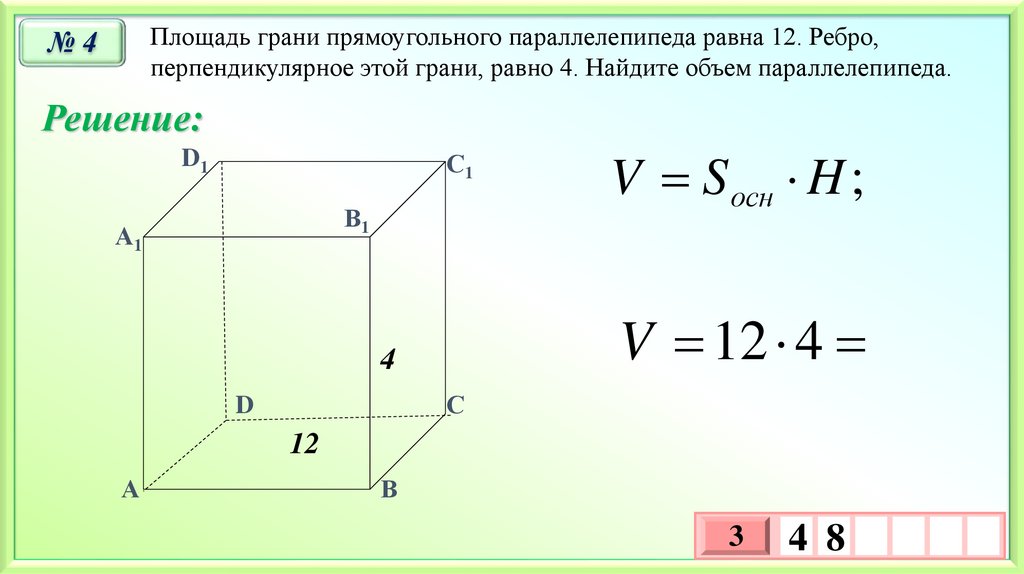
Площадь грани прямоугольного параллелепипеда равна 12. Ребро,
перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.
№4
Решение:
D1
С1
В1
А1
V S осн H ;
V 12 4
4
С
D
12
А
В
3
4 8
3
10 х
х

8.

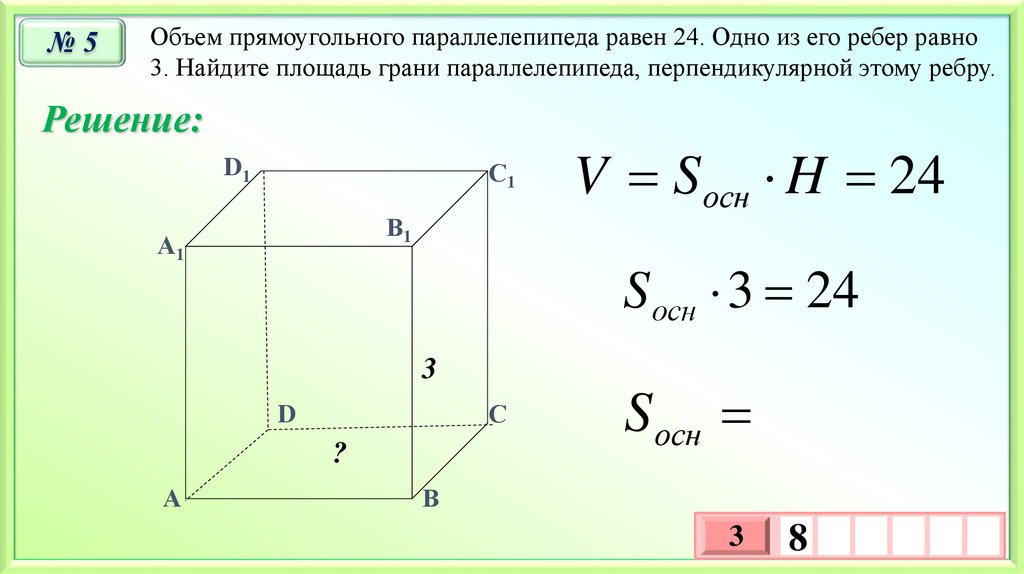
№5
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно
3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.
Решение:
D1
С1
В1
А1
S осн 3 24
3
С
D
?
А
V S осн H 24
S осн
В
3
8
3
10 х
х

9.

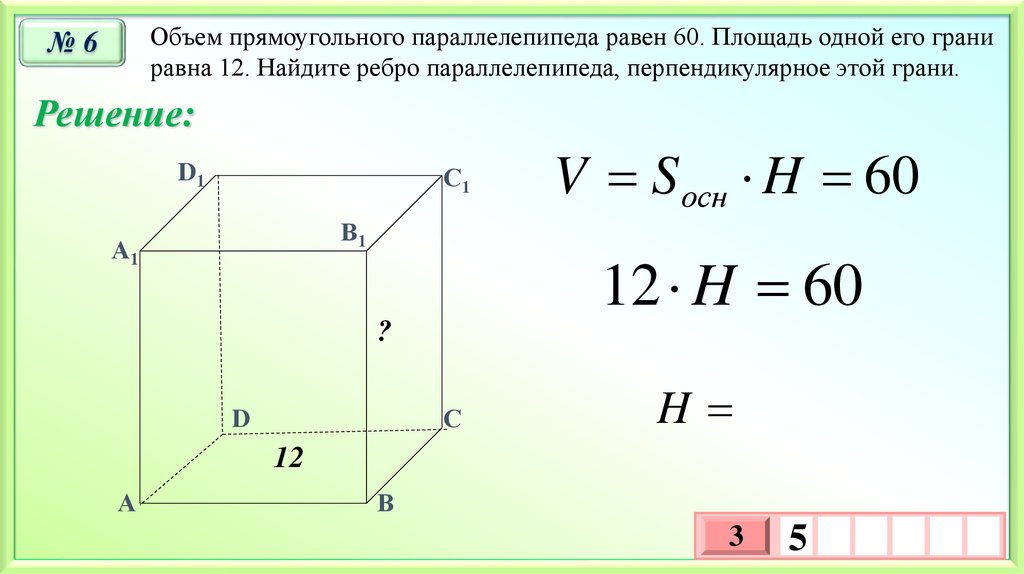
Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани
равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.
№6
Решение:
D1
С1
В1
А1
V S осн H 60
12 H 60
?
С
D
H
12
А
В
3
5
3
10 х
х

10.

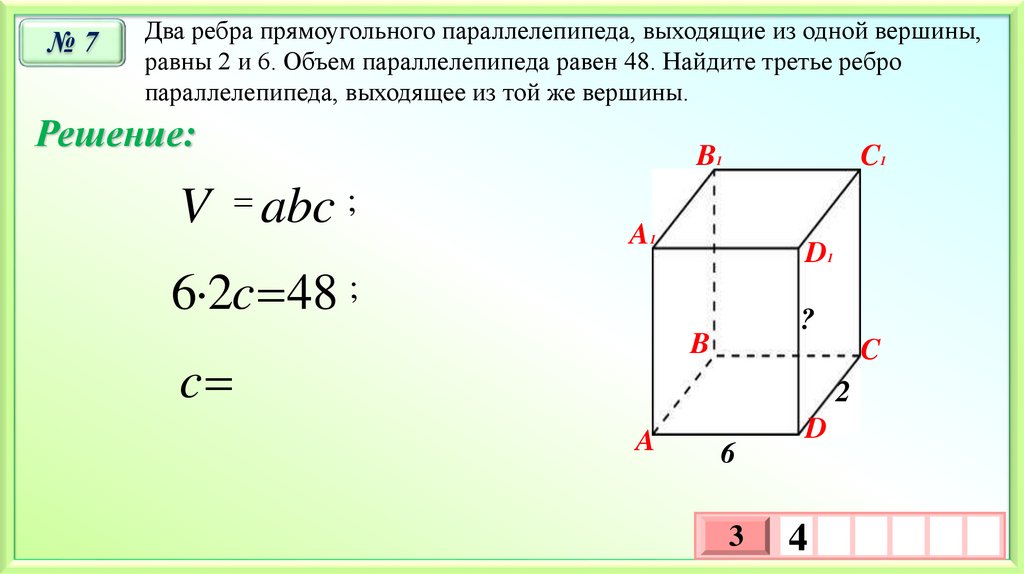
№7
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро
параллелепипеда, выходящее из той же вершины.
Решение:
V abc ;
B1
C1
A1
D1
6 2c 48 ;
?
B
c
C
2
A
6
3
D
4
3
10 х
х

11.

№8
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Решение:
V 4 6 9;
Vк а ;
3
а 4 6 9 2 2 2 3 3 3 2 3
3
3
3
6
3
10 х
х

12.

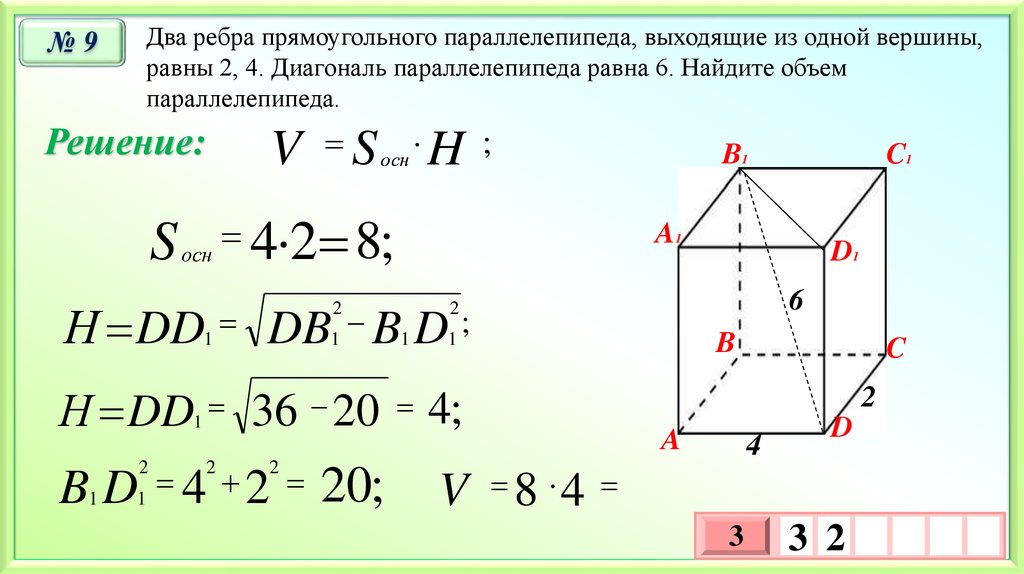
№9
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем
параллелепипеда.
V S H ;
Решение:
S
B1
осн
4 2 8;
осн
A1
Н DD1
1
1
1
2
2
1
2
B
1
36 20 4;
B D 4 2 20;
2
D1
6
Н DD DB B D ;
2
1
C1
C
2
A
4
D
V 8 4
3
3 2
3
10 х
х

13.

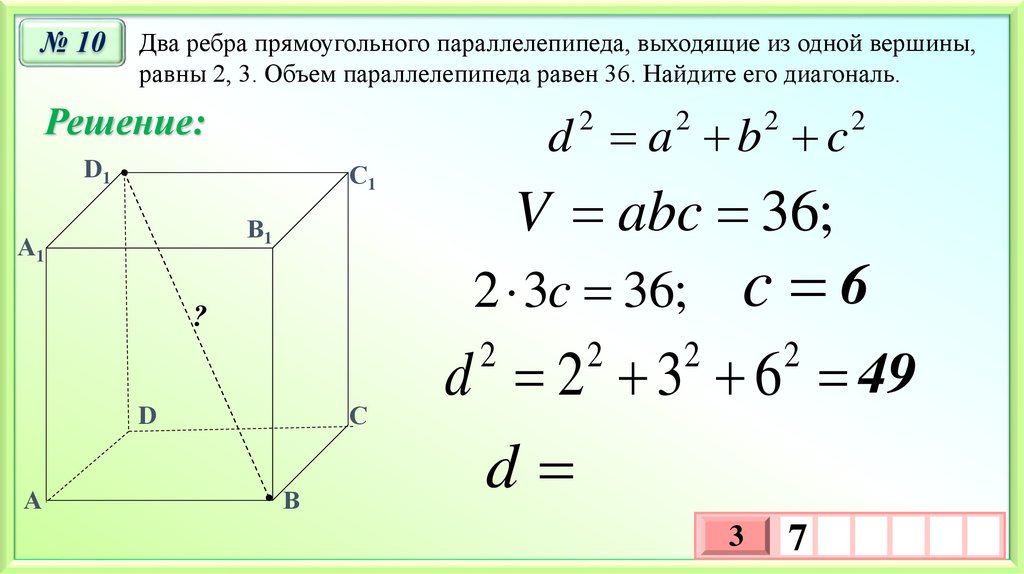
№ 10
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Решение:
d a b c
2
D1
С1
2 3c 36;
?
С
А
В
2
c 6
d 2 3 6 49
d
2
D
2
V abc 36;
В1
А1
2
2
2
2
3
7
3
10 х
х

14.

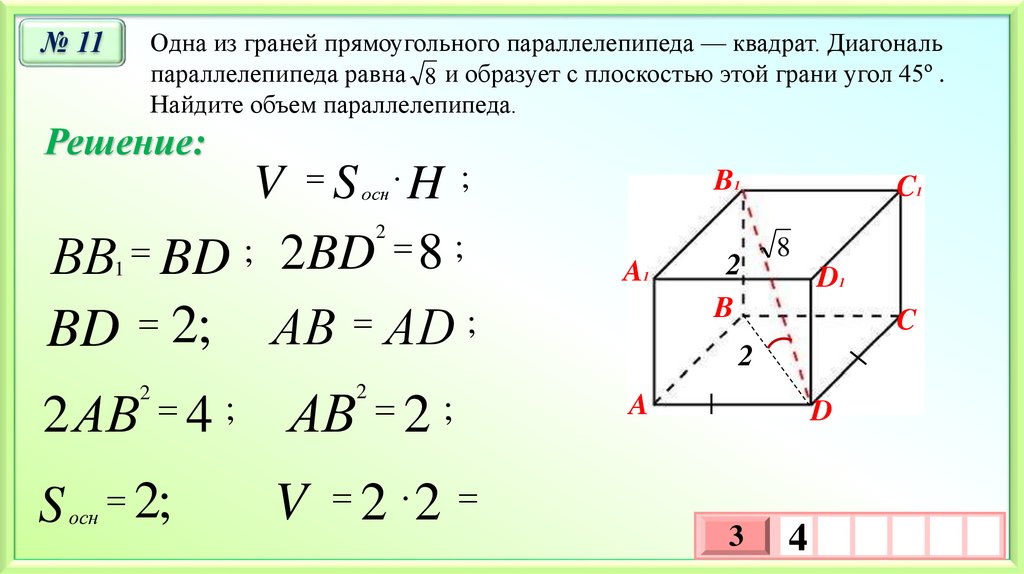
№ 11
Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ
параллелепипеда равна 8 и образует с плоскостью этой грани угол 45º .
Найдите объем параллелепипеда.
Решение:
V S H ;
2
;
;
8
2
BD
ВВ1 BD
B1
осн
BD 2;
АВ АD ;
2
2 АВ 4 ;
АВ 2 ;
2;
V 2 2
S
осн
2
A1
2
B
C1
8
D1
C
2
A
ǀ
D
3
4
3
10 х
х

15.

№ 12
Ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 1, 2, 3. Найдите его площадь поверхности.
Решение:
S 2ab 2bc 2ac
2 1 2 2 2 3 2 1 3
3
2 2
3
10 х
х

16.

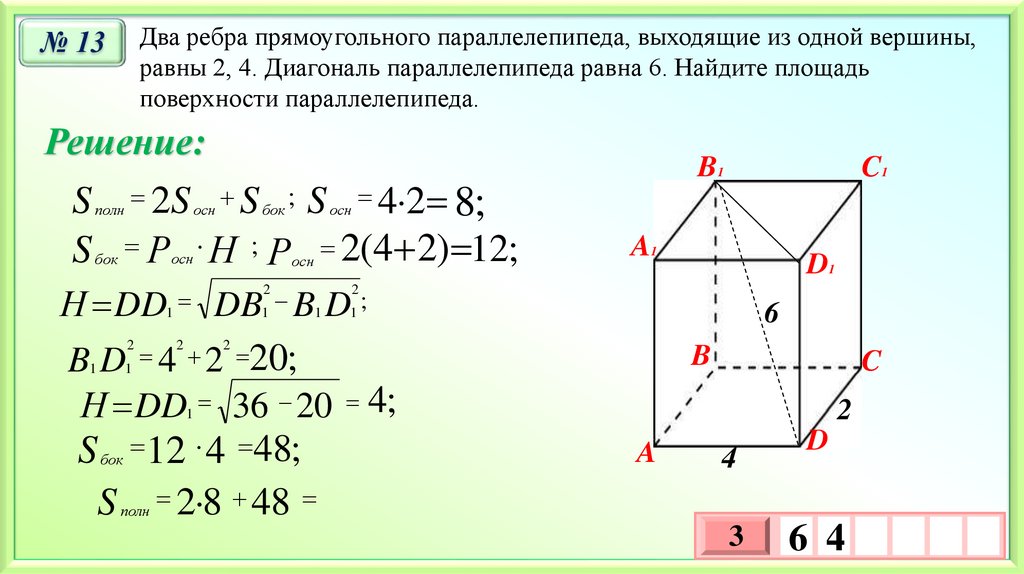
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь
поверхности параллелепипеда.
№ 13
Решение:
S
S
полн
2S осн S бок ; S осн 4 2
B1
8;
Росн Н ; Росн 2(4 2) 12;
бок
Н DD1
A1
2
D1
DB1 B1 D1 ;
2
2
6
B1 D1 4 2 20;
2
C1
2
B
C
Н DD 36 20 4;
2
1
S 12 4 48;
S 2 8 48
бок
A
4
D
полн
3
6 4
3
10 х
х

17.

№ 14
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины,
равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его
поверхности.
Решение:
S 2ab 2bc 2ac
V abc 6; 1 2c 6; c 3
S 2 1 2 2 2 3 2 1 3
3
2 2
3
10 х
х

18.

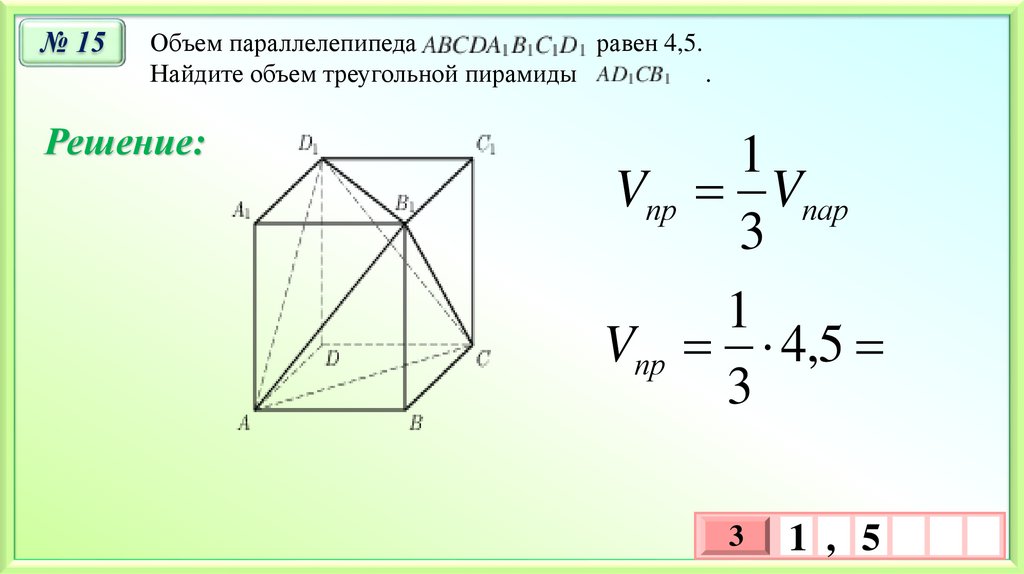
№ 15
Объем параллелепипеда
равен 4,5.
Найдите объем треугольной пирамиды
.
Решение:
1
Vпр Vпар
3
1
Vпр 4,5
3
3
1 , 5
3
10 х
х

19.

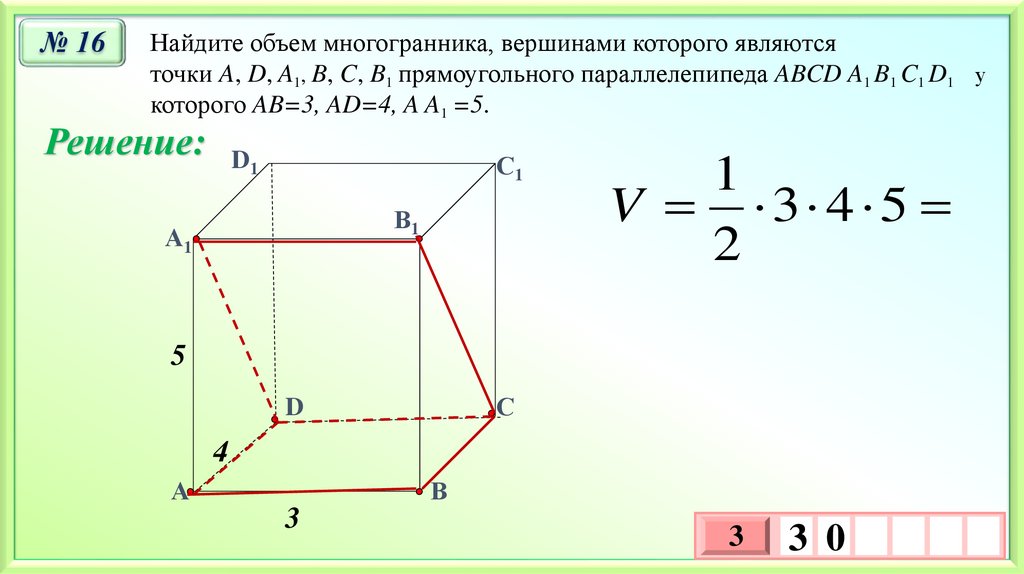
№ 16
Найдите объем многогранника, вершинами которого являются
точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCD A1 B1 C1 D1 у
которого AB=3, AD=4, A A1 =5.
Решение: D
С1
1
В1
А1
1
V 3 4 5
2
5
С
D
4
А
В
3
3
3 0
3
10 х
х

20.

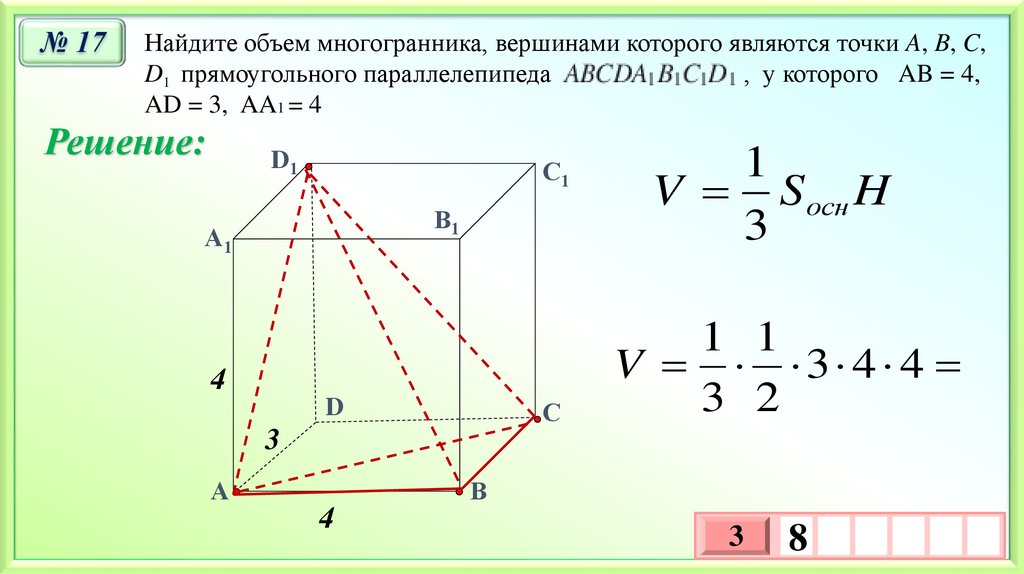
№ 17
Найдите объем многогранника, вершинами которого являются точки A, B, C,
D1 прямоугольного параллелепипеда
, у которого AB = 4,
AD = 3, AA1 = 4
Решение:
D1
С1
В1
А1
4
D
С
1
V S осн H
3
1 1
V 3 4 4
3 2
3
А
В
4
3
8
3
10 х
х

21.

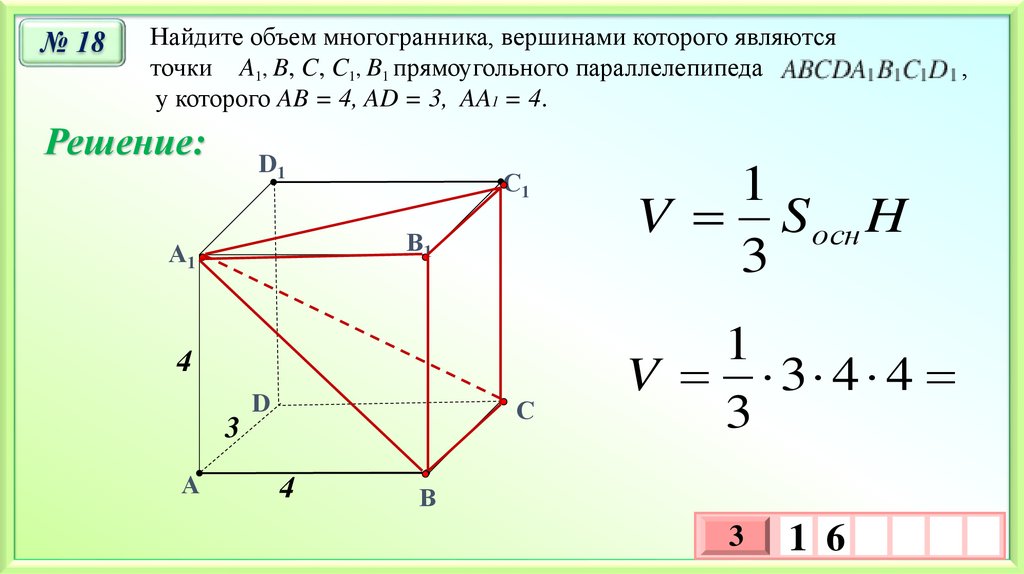
№ 18
Найдите объем многогранника, вершинами которого являются
точки A1, B, C, C1, B1 прямоугольного параллелепипеда
у которого AB = 4, AD = 3, AA1 = 4.
Решение:
D1
С1
В1
А1
4
3
А
D
С
4
,
1
V S осн H
3
1
V 3 4 4
3
В
3
1 6
3
10 х
х

22.

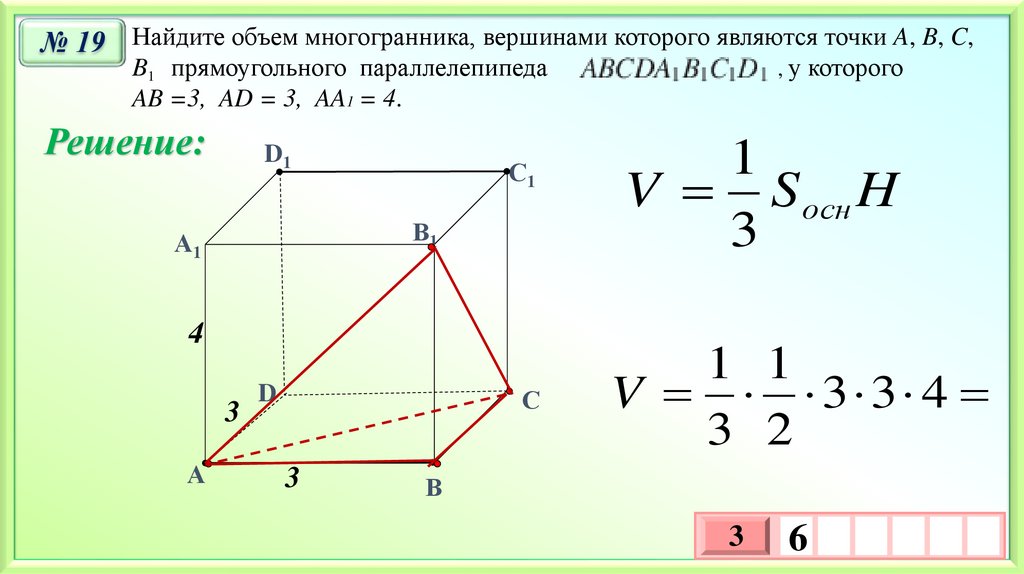
№ 19 Найдите объем многогранника, вершинами которого являются точки A, B, C,
B1 прямоугольного параллелепипеда
AB =3, AD = 3, AA1 = 4.
Решение:
D1
С1
В1
А1
4
3
А
D
С
3
, у которого
1
V S осн H
3
1 1
V 3 3 4
3 2
В
3
6
3
10 х
х

23.

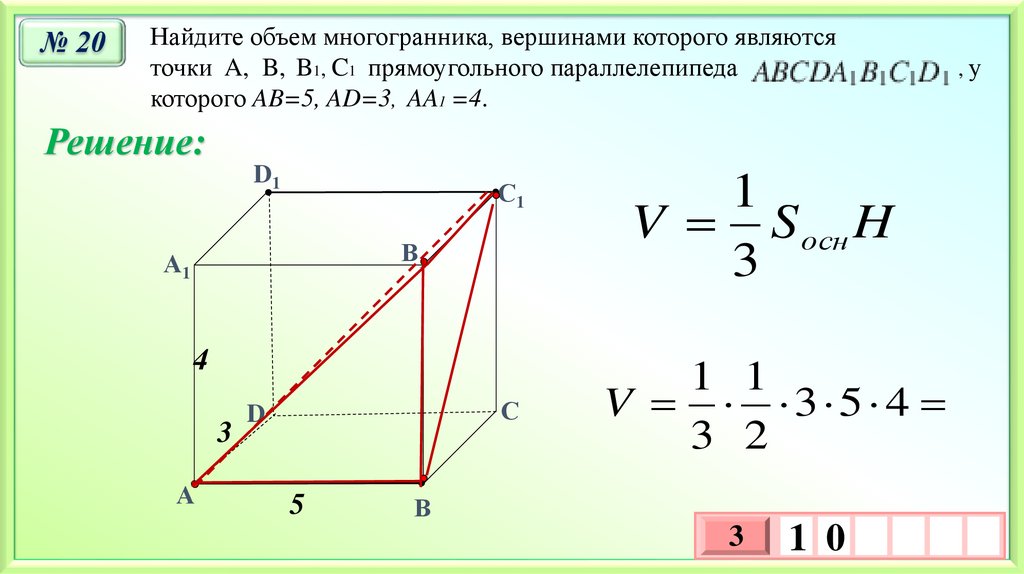
№ 20
Найдите объем многогранника, вершинами которого являются
точки A, B, B1, C1 прямоугольного параллелепипеда
которого AB=5, AD=3, AA1 =4.
,у
Решение:
D1
С1
В1
А1
4
3
А
С
D
5
1
V S осн H
3
1 1
V 3 5 4
3 2
В
3
1 0
3
10 х
х

24.

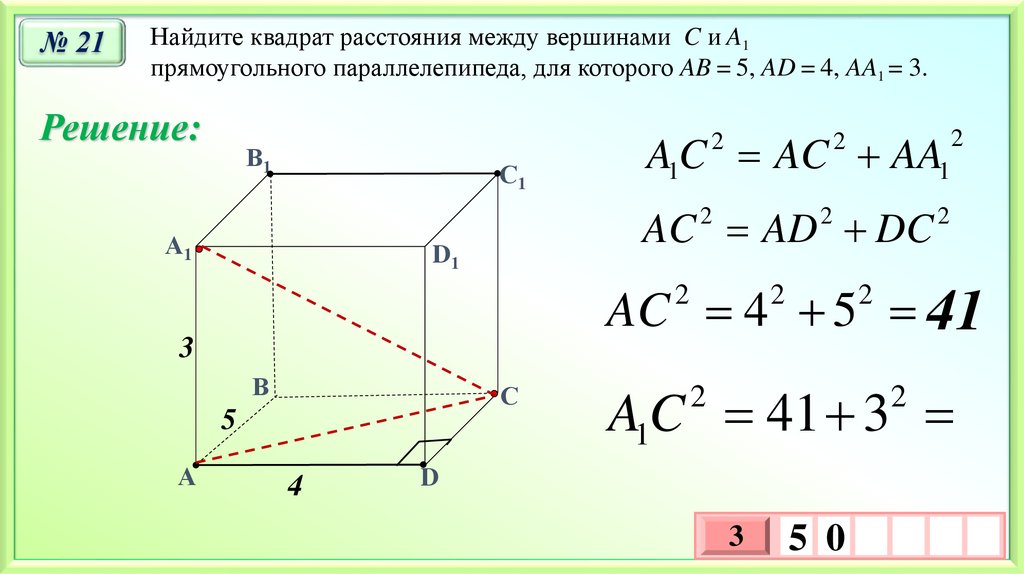
№ 21
Найдите квадрат расстояния между вершинами C и A1
прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
Решение:
A1C AC AA1
2
В1
С1
2
AC AD DC
2
А1
D1
2
2
AC 4 5 41
2
3
В
С
5
А
2
4
2
2
A1C 41 3
2
2
D
3
5 0
3
10 х
х

25.

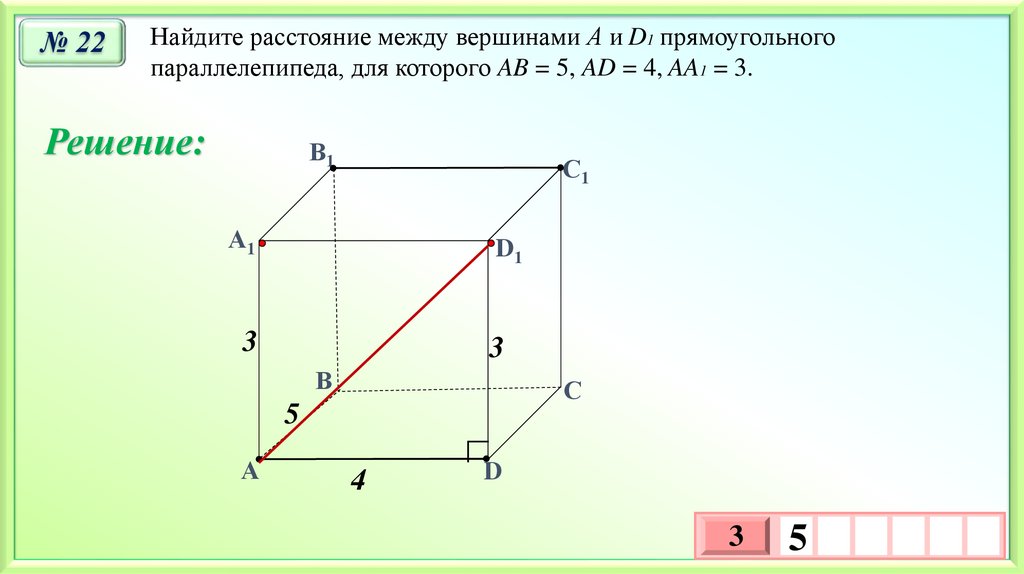
№ 22
Найдите расстояние между вершинами А и D1 прямоугольного
параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
Решение:
В1
С1
А1
D1
3
3
В
С
5
∟
А
4
D
3
5
3
10 х
х

26.

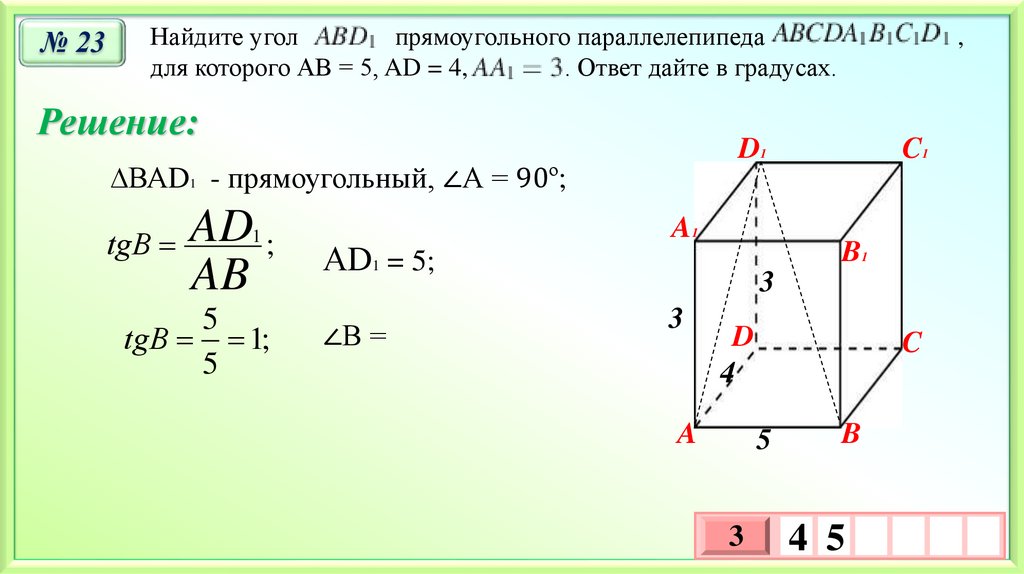
№ 23
Найдите угол
прямоугольного параллелепипеда
для которого АВ = 5, AD = 4,
. Ответ дайте в градусах.
Решение:
D1
∆ВАD1 - прямоугольный, ∠А = 90º;
tgВ AD ;
AB
1
5
tgВ 1;
5
АD1 = 5;
∠В =
,
A1
C1
B1
3
3
D
4
A
C
5
3
B
4 5
3
10 х
х

27.

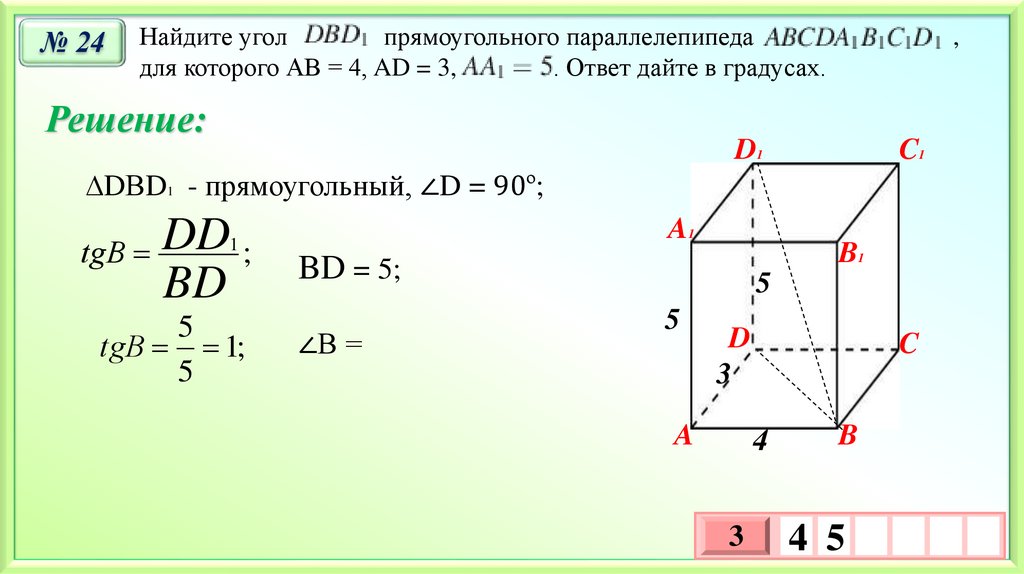
№ 24
Найдите угол
прямоугольного параллелепипеда
для которого АВ = 4, AD = 3,
. Ответ дайте в градусах.
Решение:
,
D1
C1
∆DВD1 - прямоугольный, ∠D = 90º;
tgВ DD ;
BD
A1
1
5
tgВ 1;
5
B1
BD = 5;
∠В =
5
5
D
3
A
C
4
3
B
4 5
3
10 х
х

28.

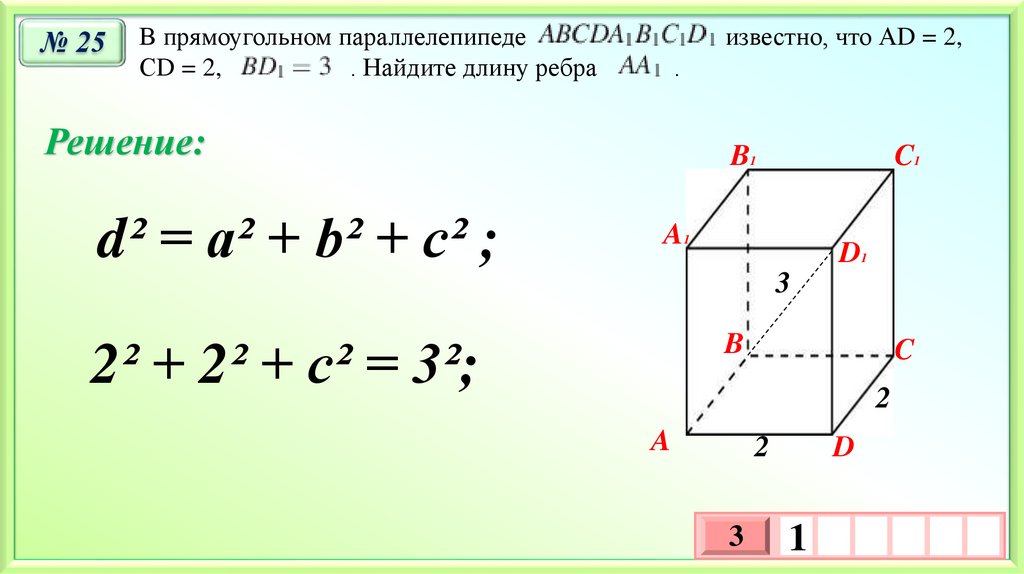
№ 25
В прямоугольном параллелепипеде
СD = 2,
. Найдите длину ребра
известно, что АD = 2,
.
Решение:
d² = a² + b² + c² ;
B1
C1
A1
D1
3
2² + 2² + c² = 3²;
B
C
2
A
2
3
D
1
3
10 х
х

29.

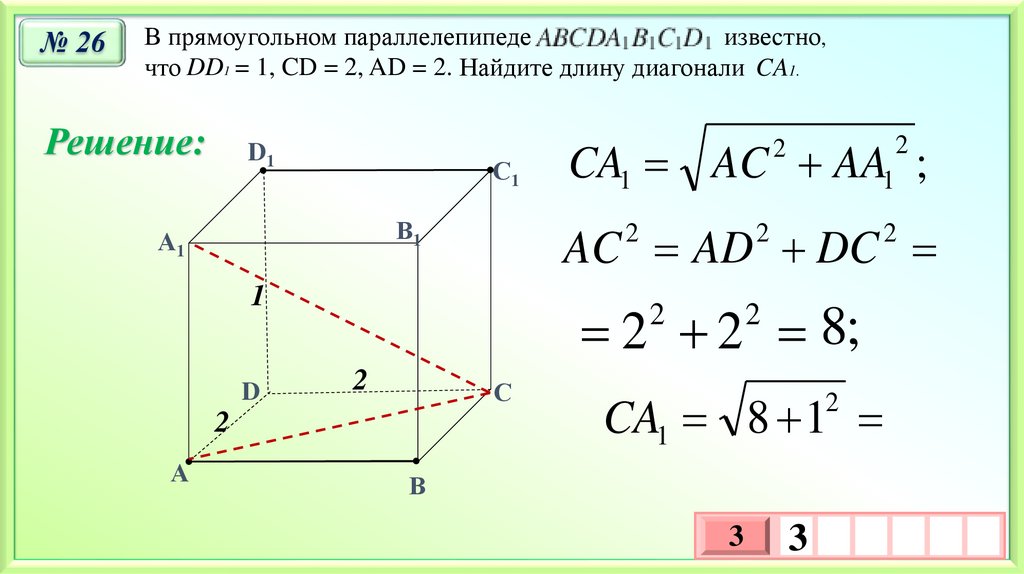
№ 26
В прямоугольном параллелепипеде
известно,
что DD1 = 1, CD = 2, AD = 2. Найдите длину диагонали CA1.
Решение:
D1
С1
AC AD DC
В1
А1
2
1
D
2
2
2 2 8;
2
2
С
2
А
CA1 AC AA1 ;
2
2
2
CA1 8 1
2
В
3
3
3
10 х
х

30.

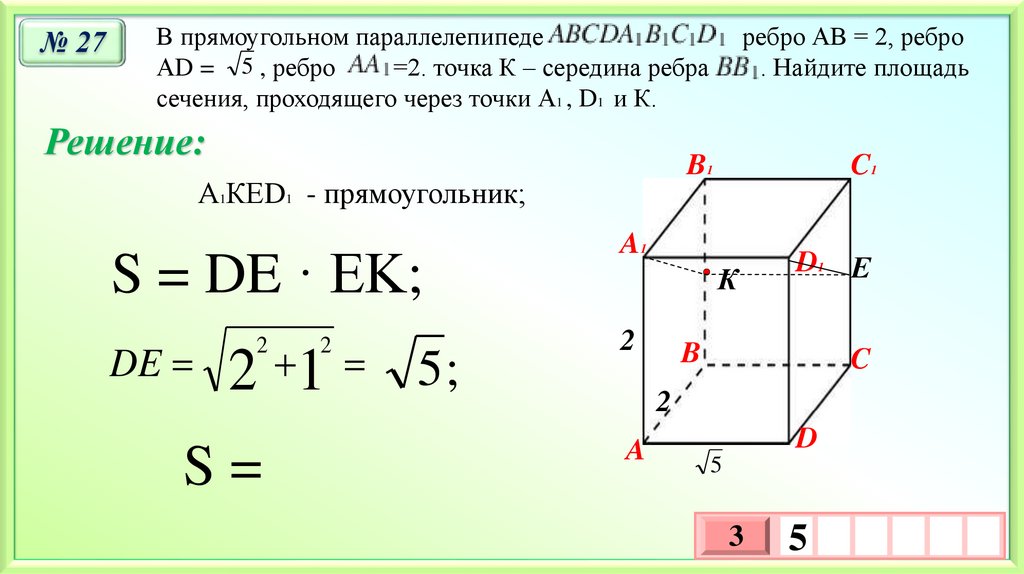
№ 27
В прямоугольном параллелепипеде
АD = 5 , ребро
=2. точка К – середина ребра
сечения, проходящего через точки А1 , D1 и К.
Решение:
B1
А1КЕD1 - прямоугольник;
S = DE · EK;
A1
DE
2
2 1
2
S=
2
5;
ребро АВ = 2, ребро
. Найдите площадь
C1
К
D1 Е
B
C
2
A
D
5
3
5
3
10 х
х

31.

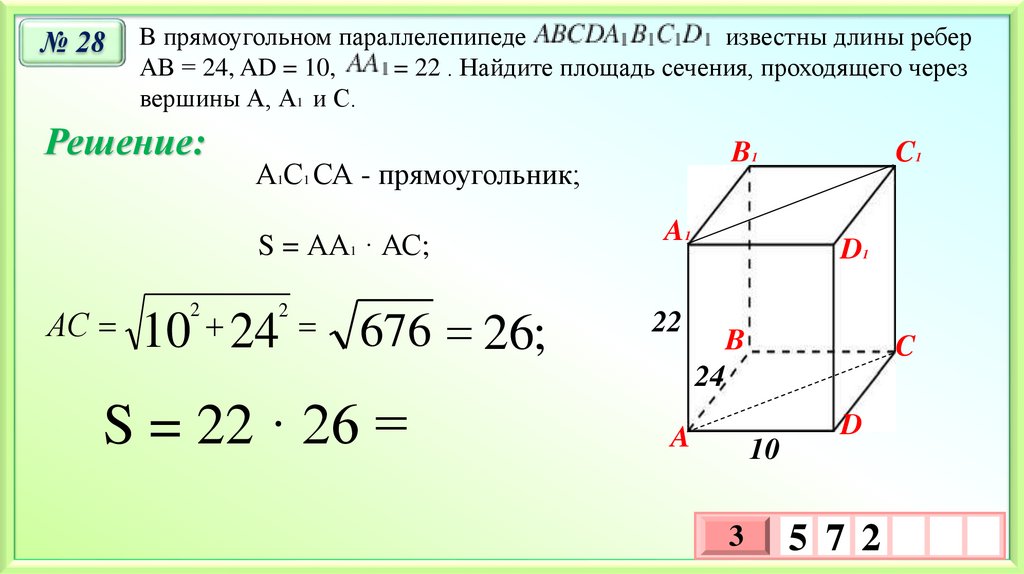
№ 28
В прямоугольном параллелепипеде
известны длины ребер
АВ = 24, AD = 10,
= 22 . Найдите площадь сечения, проходящего через
вершины А, А1 и С.
Решение:
А1С1 СА - прямоугольник;
S = АА1 · АС;
АС
10 24
2
B1
2
676 26;
S = 22 · 26 =
A1
C1
D1
22
B
C
24
A
10
3
D
5 7 2
3
10 х
х

32.

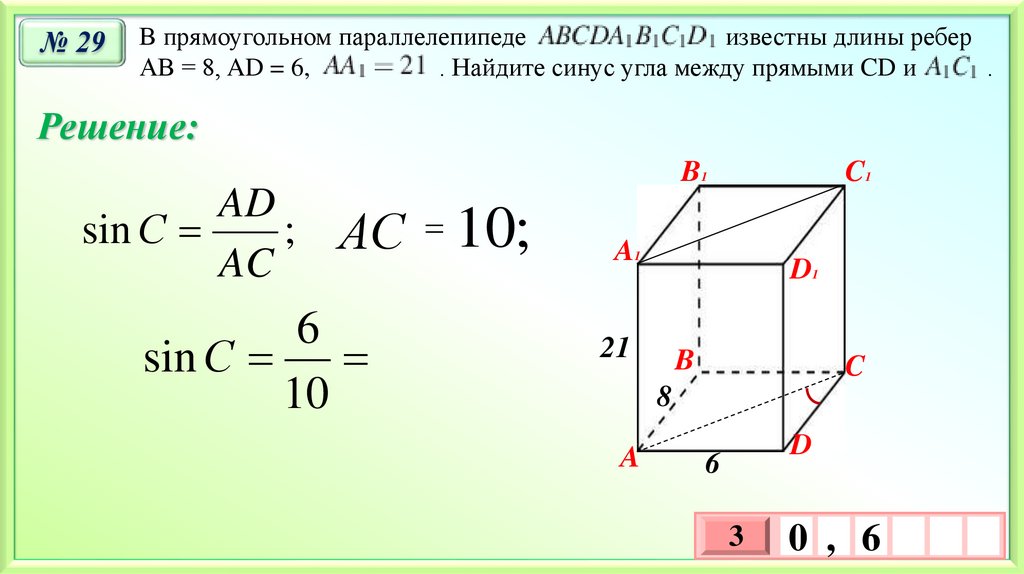
№ 29
В прямоугольном параллелепипеде
известны длины ребер
АВ = 8, AD = 6,
. Найдите синус угла между прямыми CD и
.
Решение:
AD
sin С
;
AC
B1
АС 10;
6
sin С
10
C1
A1
D1
21
B
C
8
A
D
6
3
0 , 6
3
10 х
х

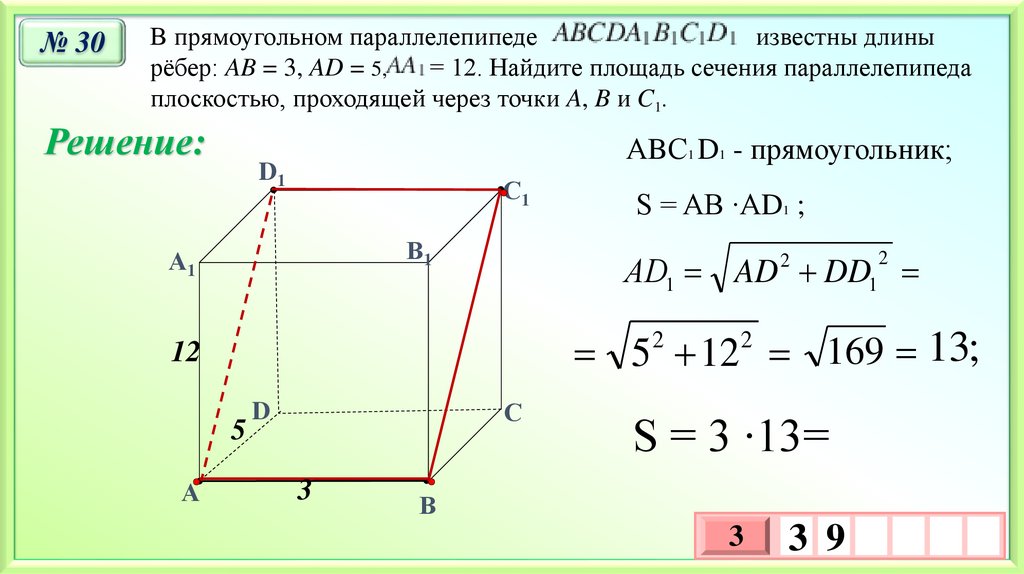
33.

№ 30
В прямоугольном параллелепипеде
известны длины
рёбер: AB = 3, AD = 5,
= 12. Найдите площадь сечения параллелепипеда
плоскостью, проходящей через точки A, B и C1.
Решение:
АBС1 D1 - прямоугольник;
D1
С1
В1
А1
АD1 AD DD1
2
2
5 12 169 13;
2
12
5
А
S = AB ∙АD1 ;
С
D
3
2
S = 3 ∙13=
В
3
3 9
3
10 х
х

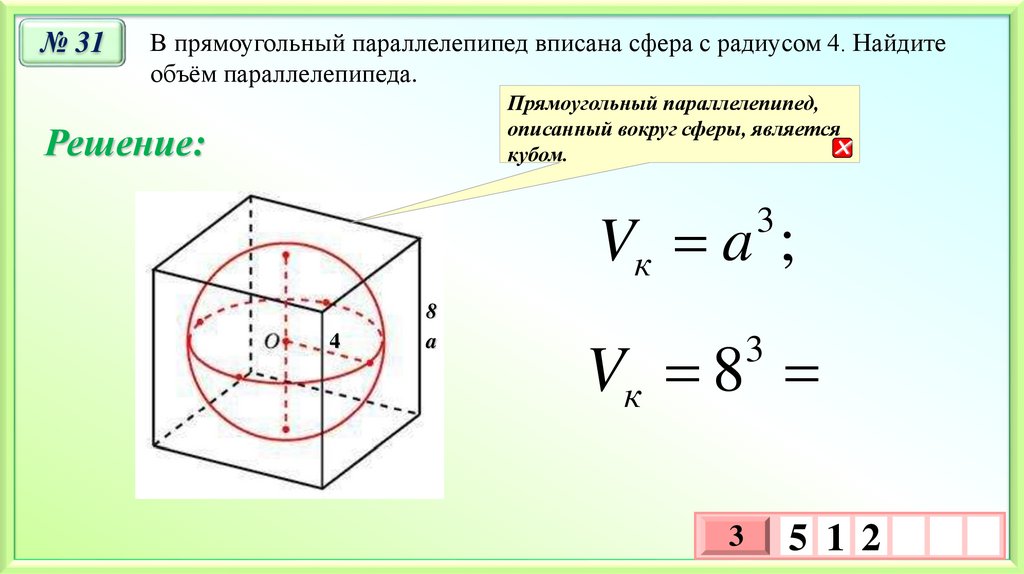
34.

№ 31
В прямоугольный параллелепипед вписана сфера с радиусом 4. Найдите
объём параллелепипеда.
Прямоугольный параллелепипед,
описанный вокруг сферы, является
кубом.
Решение:
Vк a ;
3
4
8
a
Vк 8
3
3
5 1 2
3
10 х
х