Л3_ТЙКС_24.10.24

1.

1

2.

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
імені ТАРАСА ШЕВЧЕНКА
Кафедра інформаційних систем та технологій
ТЕОРІЯ ЙМОВІРНОСТЕЙ та КОМП'ЮТЕРНА СТАТИСТИКА
Викладачі: Володимир ДРУЖИНІН; Ганна ТЕРЕЩУК
2024

3.

ЛЕКЦІЯ № 3. Частина 1: «Дискретні і неперервні випадкові величини, їх
розподіли та числові характеристики»
3

4.

1. Види випадкових величин
Випадковою називається величина, яка при кожному проведенні
випробування набуває певного значення з множини можливих значень, причому
заздалегідь невідомо, якого саме.
Відмінність від випадкової події досить істотна: якщо випадкова подія може
або відбутися, або не відбутися в результаті випробування, то випадкова величина
в результаті випробування обов’язково приймає деяке значення.
!!! Можна вважати, що випадкова подія є окремим випадком випадкової
величини, яка приймає тільки два значення – одне, наприклад, 1 – «подія
відбулася», друге 0 – «подія не відбулася».
Таким чином, випадкова подія є якісним вираженням випадкової величини, а
поняття «випадкова величина» є розвиненням, узагальненням поняття «випадкова
подія».
4

5.

!!! Використання випадкових величин дає можливість виконати більш повний,
детальніший аналіз ймовірнісних явищ.
ПРИКЛАД. Якщо в якості випробування розглядати здавання студентом
іспиту, то можна говорити про випадкову подію «студент здав іспит», а можна –
про випадкову величину «отримана оцінка», яка може набути одного зі значень
2, 3, 4, 5.
!!! Очевидно, що величина оцінки дає повнішу інформацію про знання
студента.
5

6.

!!! Випадкові величини можуть бути дискретними і неперервними.
Дискретною випадковою величиною називається така випадкова величина,
число можливих значень якої є скінченною або зліченною множиною.
*** Злічена множина – це така нескінченна множина, елементи якої можна
пронумерувати за допомогою множини натуральних чисел.
!!! Самостійно наведіть приклади дискретних випадкових величин.
6

7.

Дискретні випадкові величини в свою чергу можна поділити на кілька
видів.
1. Кількісна випадкова величина, яка дозволяє кількісно вимірювати
показник за деякою шкалою.
Приклад. Кількість автобусів на лінії, кількість студентів в аудиторії,
кількість необхідного покупцю товару і тому подібне.
7

8.

Ординальна (порядкова) випадкова величина дозволяє тільки
упорядкувати досліджені об’єкти за ступенем виявлення в них аналізованої якості.
*** Такі величини використовуються, коли шкала кількісного вимірювання
відсутня або невідома.
ПРИКЛАД. При дослідженні житлових умов звичайно виділяють групи:
А – погані житлові умови,
Б – задовільні,
В – добрі,
Г – дуже добрі.
8

9.

3. Номінальна (класифікаційна) випадкова величина дозволяє тільки
поділити об’єкти за аналізованою якістю на однорідні групи (класи), що не
піддаються упорядкуванню.
*** Це такі якості як стать студента (хлопець – дівчина), професія
батьків і тому подібне.
9

10.

!!! Найпоширенішим випадком є кількісна випадкова величина і саме такі
величини розглядаються зазвичай в теорії ймовірностей.
10

11.

Неперервною випадковою величиною називається така випадкова
величина, яка може приймати будь-які значення з деякого інтервалу числової осі
(обмеженого чи нескінченного).
ПРИКЛАДИ - час очікування автобуса; розміри деталей, виготовлених
робітником за зміну і інші.
!!! Додати своъ приклади неперервних випадкових величин.
*** При обробці деталей існують допуски на їхні розміри.
Припустимо, що всі деталі відповідають стандарту. Проте їхні розміри є
неперервною випадковою величиною, тому що вони можуть приймати будь-яке значення
всередині заданого інтервалу допуску. Якщо навіть ми одержимо при вимірюванні, що дві
деталі мають однакові розміри, то, підвищивши точність вимірів, ми переконаємося, що
розміри відрізняються в наступному знаку.
!!! Таким чином, всі можливі значення неперервних випадкових величин не
можна пронумерувати за допомогою множини натуральних чисел.
11

12.

Випадкові величини прийнято позначати заголовними (великими) буквами
латинської абетки
Х, Y, Z , ...,
а їх можливі числові значення – відповідними малими літерами:
х1, х2, ..., хn – можливі значення дискретної випадкової величини Х;
y – поточне значення неперервної випадкової величини Y.
12

13.

2. Закон розподілу випадкової величини
У результаті випробування випадкова величина набуває одного зі своїх
можливих значень.
!!! Отже, певну інформацію про випадкову величину можна задати
перерахуванням всіх можливих значень або вказівкою інтервалу можливих
значень.
!!! Але така інформація буде неповною.
ПРИКЛАД. Якщо студент Іваненко старанно вивчав дисципліну протягом всього
семестру, то він скоріш за все отримає оцінку «відмінно».
Якщо ж студент Петренко лише за 5 хвилин до іспиту дізнався, що така дисципліна
вивчалася в цьому семестрі, то він скоріш за все отримає оцінку «незадовільно».
!!! Хоча можливі значення випадкової величини в обох випадках однакові, ймовірність
набуття конкретних значень різна.
13

14.

!!! Для повної характеристики випадкової величини необхідно враховувати як
її можливі значення, так і ймовірності набуття цих значень, що досягається за
допомогою закону розподілу.
Законом розподілу випадкової величини називається будь-яка
відповідність, що встановлює зв’язок між можливими значеннями випадкової
величини і ймовірностями набуття цих значень.
*** Форми завдання закону розподілу можуть бути:
- табличні;
- графічні;
- аналітичні.
14

15.

У випадку дискретної випадкової величини найзручнішою формою закону
розподілу є ряд розподілу.
Він являє собою таблицю, в якій перераховані всі можливі значення
випадкової величини і відповідні їм імовірності:
*** Символом рі позначено ймовірність того, що випадкова величина прийме
своє і-те значення, тобто хі.
Останній факт зазвичай позначають так:
рі = Р(Х = хі ).
15

16.

!!! Ряд розподілу придатний тільки для дискретної випадкової величини,
оскільки для неперервної випадкової величини просто неможливо перерахувати
всі можливі значення.
16

17.

Приклад. По мішені тричі стріляють з рушниці, причому ймовірність
влучення в мішень при кожному пострілі дорівнює 0,7. Випадкова величина Х –
кількість влучень у мішень.
Ряд розподілу випадкової величини в данному випадку буде мати вигляд:
!!! У ряді розподілу – сума ймовірностей, що входять до ряду розподілу,
дорівнює 1.
*** Дійсно, у ряді розподілу повинні бути перераховані всі можливі значення
випадкової величини, тому події
Х = хі (і = 1,2,..., n)
утворюють повну групу несумісних подій, сума ймовірностей яких дорівнює 1.
17

18.

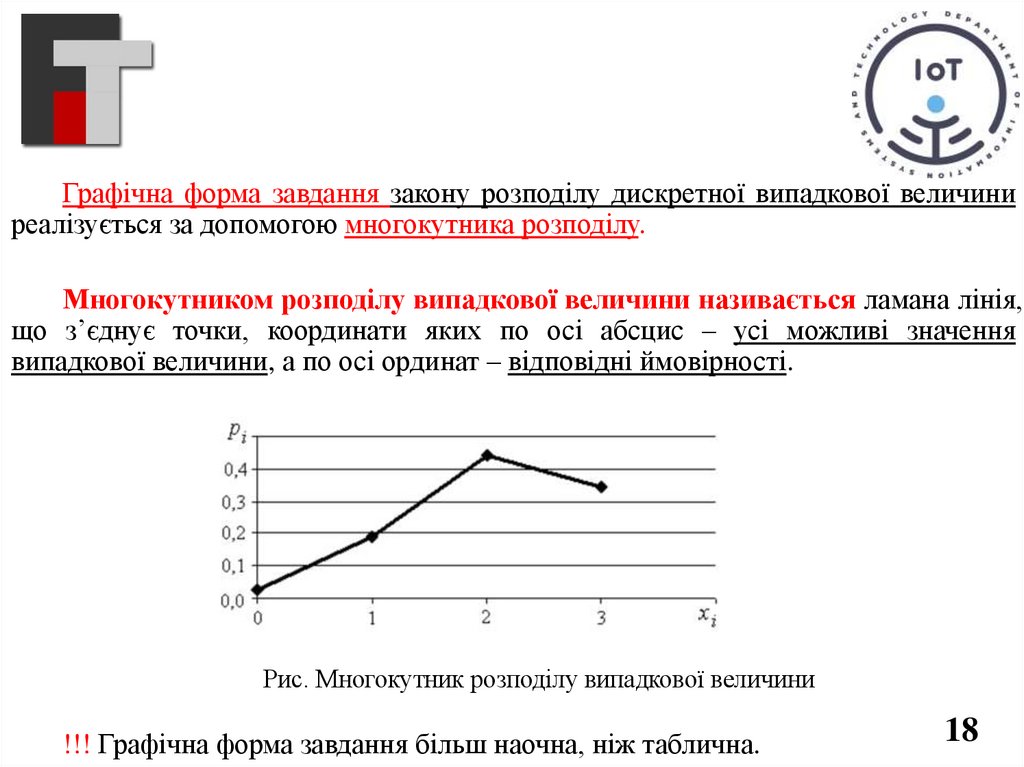
Графічна форма завдання закону розподілу дискретної випадкової величини
реалізується за допомогою многокутника розподілу.
Многокутником розподілу випадкової величини називається ламана лінія,
що з’єднує точки, координати яких по осі абсцис – усі можливі значення
випадкової величини, а по осі ординат – відповідні ймовірності.
Рис. Многокутник розподілу випадкової величини
!!! Графічна форма завдання більш наочна, ніж таблична.
18