669baeff3177d31deb226b4f9e42c630

1.

Тема:
«Определитель и его вычисление»

2.

Тема: «Определитель и его
вычисление».
Цель: 1. Изучить свойства определителей и способы их вычисления.
2. Научиться производить расчёты определителей разными способами.
Ход занятия
1. Повторение определения «Матрица».
2. Объяснение нового материала.
а) Вычисление определителей 2-го порядка.
б) Вычисление определителей 3-го порядка.
в) Теорема о разложении определителя по элементам строки
или столбца.
3. Закрепление нового материала.
4. Практическая работа.

3.

Определение:
Матрицей размером m n называется
прямоугольная таблица чисел, содержащая m строк и
n столбцов.
a11 a12 ..... a1n
Am n a 21 a 22 ..... a 2 n
a a ..... a
mn
m1 m 2

4.

Причины важности изучения определителей и их
вычисление:
В школьном курсе алгебры 7 – 9 классов рассматриваются различные способы
решения систем линейных уравнений: метод подстановки, метод сложения, метод
двойного сложения, графический метод, метод сравнения. Кроме методов,
изучаемых в школе, существуют и другие, доступные для учащихся старших
классов и студентов методы решения систем линейных уравнений: метод
Крамера, метод Гаусса, матричный метод. Эти методы способствуют развитию
внимания, памяти.
Историческая справка
Первые упоминания об определителях относится концу 17-го века, когда
немецкий математик Лейбниц изучал линейные уравнения с многими
неизвестными. Далее в конце 18-го века швейцарский математик Крамер указал
общий закон составления определителей и привел формулы для решения систем
линейных уравнений с n- неизвестными с помощью определителей.
В настоящее время нет почти ни одной отрасли математики, в которой не имели
бы приложений определители. Они встречаются в алгебре, в аналитической
геометрии, механике, в теории функций, в линейном программировании и т.д.

5.

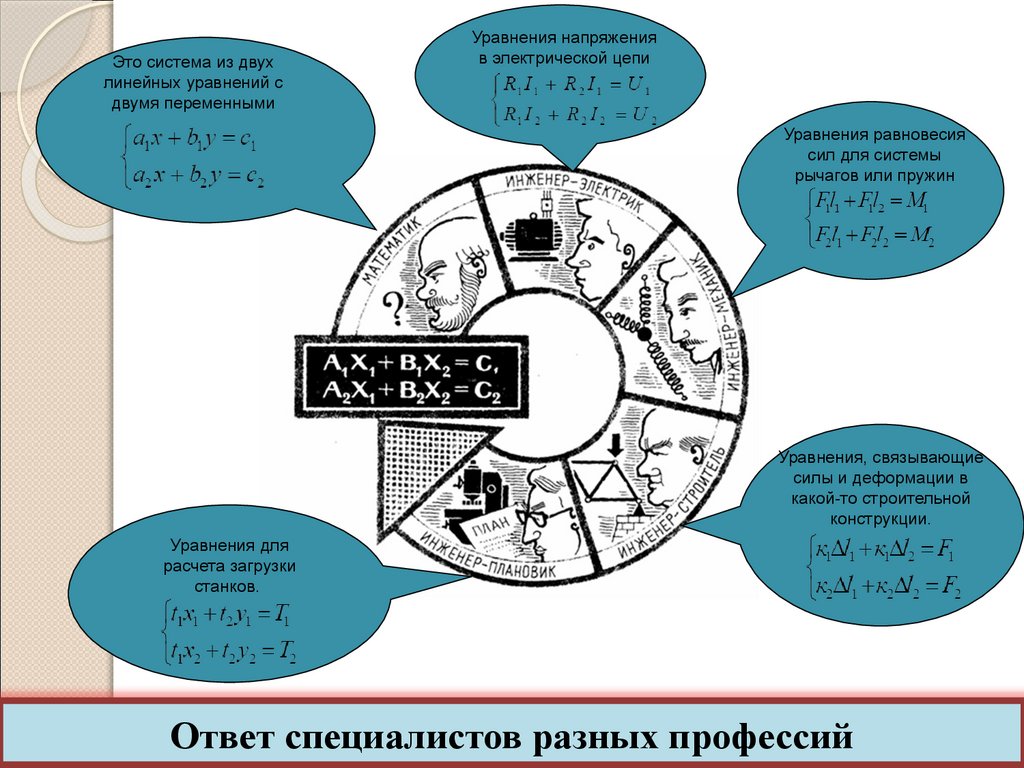
Это система из двух
линейных уравнений с
двумя переменными
Уравнения напряжения
в электрической цепи
Уравнения равновесия
сил для системы
рычагов или пружин
Уравнения, связывающие
силы и деформации в
какой-то строительной
конструкции.
Уравнения для
расчета загрузки
станков.
Ответ специалистов разных профессий

6.

Определение:
a11 a12 ..... a1n
Любой квадратной матрице n-го порядка А a21 a22 ..... a2 n
a
a
.....
a
n2
nn
n1
можно поставить в соответствие выражение, которое называется
определителем (детерминантом) матрицы А, и обозначается так:
| A | = det A= ∆ =
a11
a12 .....
a1n
a21
a22 .....
a2 n
an1
an 2 .....
ann

7.

1. Определитель второго порядка задаётся
равенством:
a11
a12
a21 a22
a11 a22 a12 a21

8.

2. Определитель третьего порядка задаётся
равенством:
a11 a12 a13
a21 a22 a23 (a11 a22 a33 ) (a21 a32 a13 ) (a12 a23 a31 )
a31 a32 a33
(a13 a22 a31 ) (a21 a12 a33 ) (a23 a32 a11 )

9.

10.

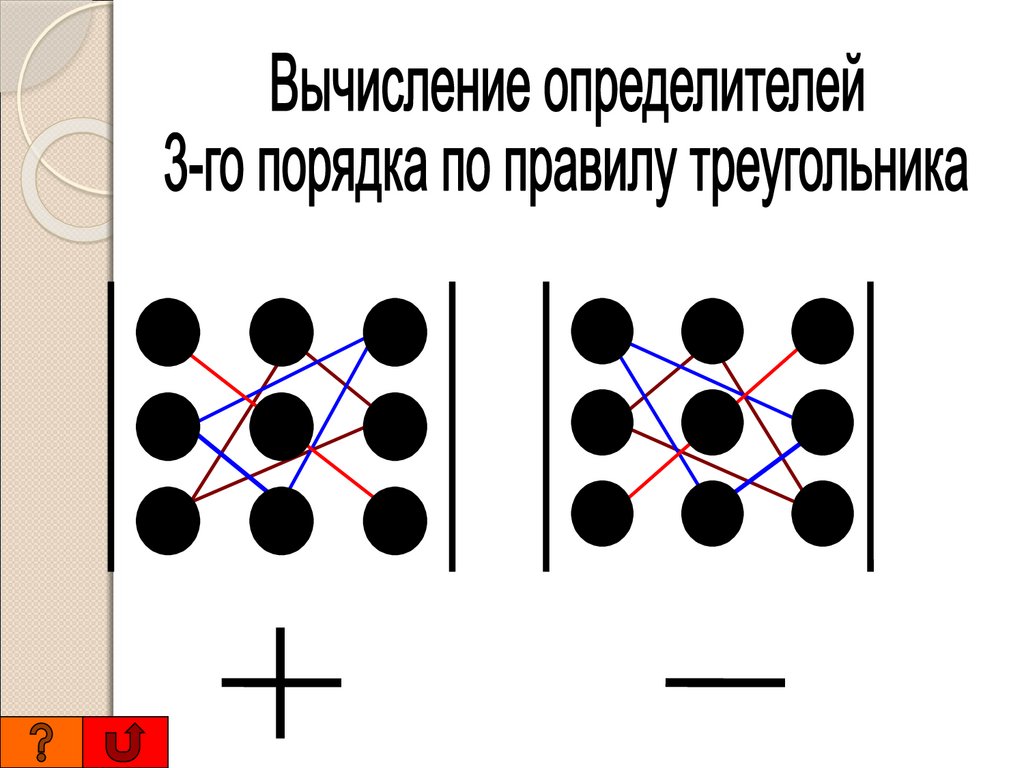
МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯ
ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
МАТРИЦ 3-го ПОРЯДКА
a11
a22
a12
a33 a31
a23 a21
a32
a13
a22
a
31
a13 a12
a21
a11
a33 a32
a23

11.

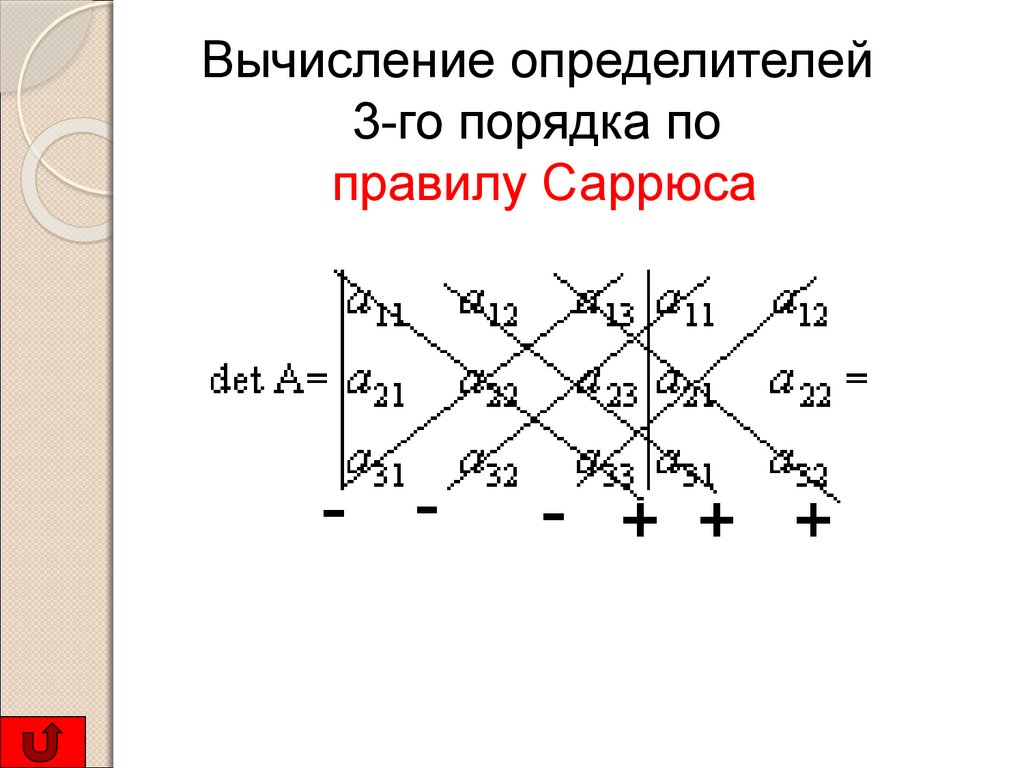
Вычисление определителей
3-го порядка по
правилу Саррюса

12.

Определение:
Минором Mij к элементу aij квадратной матрицы А,
называется определитель, составленный из элементов
матрицы А, оставшихся после вычёркивания i-строки и jстолбца.
Определение:
Алгебраическим дополнением Aij к элементу aij
квадратной матицы А, называется произведение:
Aij=(-1)i+j ·Mij

13.

Теорема: (о разложении определителя по элементам
строки или столбца).
Сумма произведений элементов любой строки (столбца)
определителя на их алгебраические дополнения равна этому
определителю, т. е.
Разложение по элементам i-строки:
∆= ai1 Ai1 ai 2 Ai 2 ... ain Ain
Разложение по элементам j-столбца:
∆=
a1 j A1 j a2 j A2 j ... anj Anj

14.

Вычисление определителей с помощью
разложения по строке или столбцу
Замечание.
1.Данная теорема справедлива для определителей,
начиная
со 2-го порядка и выше, но целесообразнее ее применять
для определителей 4-го порядка и выше.
2.Методы вычисления определителей n-го порядка:
эффективного понижения порядка и сведения к
треугольному виду.

15.

ПРИМЕР ВЫЧИСЛЕНИЯ
ОПРЕДЕЛИТЕЛЯ
РАЗЛОЖИМ ОПРЕДЕЛИТЕЛЬ ПО 2-й СТРОКЕ
3 1 2
1 2
3 2
4 2 0 ( 1) 2 1 ( 1) 2 2 0
7 9 1
9 1
7 1
( 1) ( 1 18) 1 (3 14) 19 11 8

16.

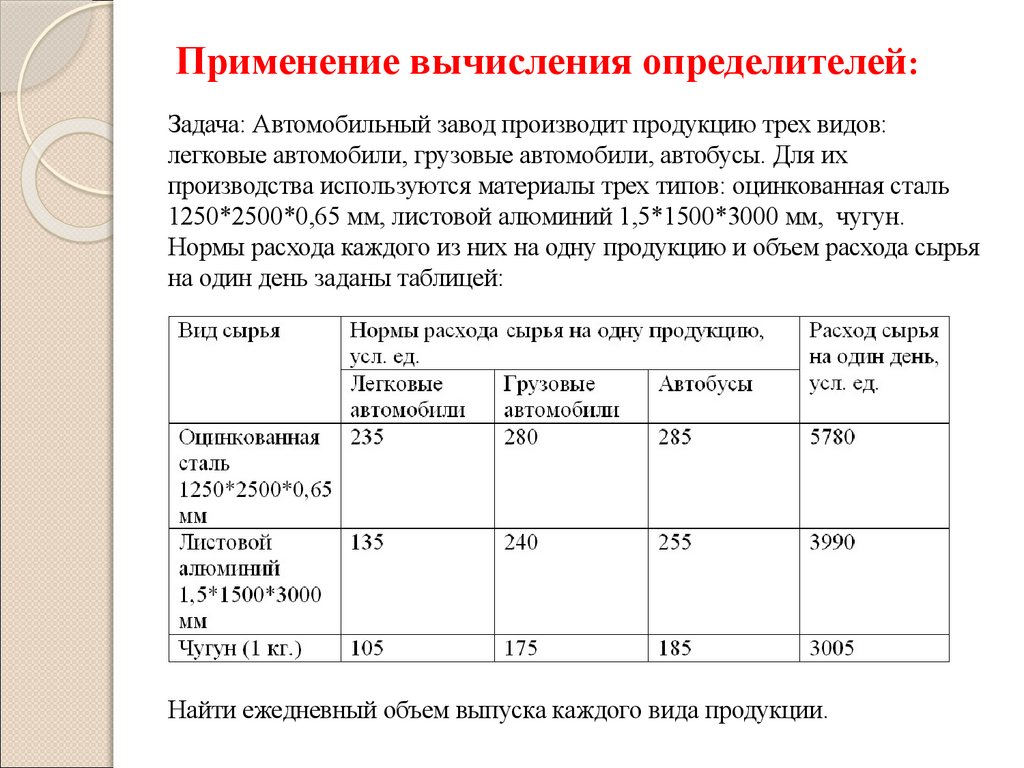
Применение вычисления определителей:
Задача: Автомобильный завод производит продукцию трех видов:
легковые автомобили, грузовые автомобили, автобусы. Для их
производства используются материалы трех типов: оцинкованная сталь
1250*2500*0,65 мм, листовой алюминий 1,5*1500*3000 мм, чугун.
Нормы расхода каждого из них на одну продукцию и объем расхода сырья
на один день заданы таблицей:
Найти ежедневный объем выпуска каждого вида продукции.

17.

Решение:
Пусть ежедневно завод выпускает x₁ легковых автомобилей, x₂
грузовых автомобилей и x₃ автобусов. Тогда в соответствии с
расходом сырья каждого вида имеем систему:
235x₁ + 280x₂ + 285x₃ = 5780
135x₁ + 240x₂ + 255x₃ = 3990
105x₁ + 175x₂ + 185x₃ = 3005
∆ = 2250
∆₁ = 33750
∆₂ = 11250
∆₃ = 6750
x₁ = 33750/2250 = 15
x₂ = 11250/2250 = 5
x₃ = 6750/2250 = 3
Ответ: фабрика выпускает 15 легковых автомобилей, 5 грузовых
автомобилей и 3 автобуса.

18.

1. Вычислить определители 2-го порядка.
3 4
6 2
2. Найти алгебраические дополнения элементов а13, a23,a12.
а2
в
ав
в2
3 5
А 1 4
6 0
3. Вычислить определители 3-го порядка всеми изученными
выше способами.
2 8 2
А 1 4
3 8
2
5
2
2
3