Похожие презентации:
5л_Интегрирование триг функций
1. 3. Классы интегрируемых функций
Интегральное исчисление3. Классы интегрируемых
функций
3.3. Интегрирование
тригонометрических функций
2. Повторим
sin t cos t 1Повторим
1
tg t 1
2
cos t
1 sin t cos t
1
2
1 tg t
2
cos t
sin 2t 2 sin t cos t
cos 2t cos t sin t
2
2
2
2
2
2
x
x
x
2tg
sin
2tg
x
x
x
2 cos 2
2
2
sin x 2 sin cos 2
1
x
2
2
2
2 x
cos
1 tg
2
2
2 x
cos
2
x
2
2 x
sin
1 tg
x
x
x
2
2
cos x cos 2 sin 2 cos 2 1
2
2
2 cos 2 x 1 tg 2 x
2
2
2
3. 1. Универсальная тригонометрическая подстановка
R(sin x; cos x)dxx
tg t
2
R – дробно-рациональная функция
x 2arctgt
2t
sin x
1 t2
x
2tg
2
sin x
2 x
1 tg
2
2
dx
dt
2
1 t
1 t 2
cos x
1 t 2
x
2
cos x
2 x
1 tg
2
1 tg 2
4. 2. Интегрирование выражений вида
R(sin x; cos x)dxR( sin x; cos x)dx R(sin x; cos x)dx
нечетная относительно sinx
t cos x
R(sin x; cos x)dx R(sin x; cos x)dx
нечетная относительно соsx
t sin x
R( sin x; cos x)dx R(sin x; cos x)dx
четная относительно sinx и соsx
t tg x
5. Таблица тригонометрических подстановок
tdt
sinx
cosx
tgx
x
dx
1
cosx
t
2
sinx
3
tgx
1
tg x 1
cos 2 x
2
t
1
t
1 t
2
1 t
2
1
cos x 2
tg x 1
2
t
sin x
tgx
cos x
6. Таблица тригонометрических подстановок
t1
dt
cosx sin xdx
2
sinx
3
tgx
cos xdx
dx
cos 2 x
sinx
1 t
2
cosx
tgx
t
1 t 2
t
t
1 t 2
t
1
1 t
2
1 t
x
dx
arccost
dt
dt
t
1 t
2
t
1 t 2
2
arcsint
1 t 2
arctgt
dt
1 t 2
7. 3. Интегрирование выражений вида
sinx
cos
xdx
,
m
Z
,
n
Z
n
m
Если m = 2k + 1 (нечетное), m > 0, то удобнее сделать подстановку
sin x = t. sin n x cos 2 k x cos xdx sin n x (1 sin 2 x) k cos xdx
Если n = 2k + 1 (нечетное), n > 0, то удобнее сделать подстановку
cos x = t. sin 2 k x cos m x sin xdx
2
k
m
(1 sin x) cos x sin xdx
Если обе степени m, n четные и положительные, то используем
формулы понижения степени
1
sin x (1 cos 2 x)
2
2
1
cos x (1 cos 2 x)
2
2
Если обе степени m, n отрицательны и их сумма четная, то
выполняем подстановку tg x = t (или сtg x = t)
8. 4. Интегрирование выражений вида
R(tgx)dxR – рациональная функция
Выполняем подстановку tg x = t (или сtg x = t)
9. 5. Интегрирование выражений вида
m, n ∈ Rsin mx cos nxdx
cos mx cos nxdx
1
sin cos (sin( ) sin( ))
2
1
cos cos (cos( ) cos( ))
2
1
sin sin (cos( ) cos( ))
2
sin mxsin nxdx
формулы
произведения
тригонометрических
функций
10. Пример
• Укажите, какой подход при интегрированииможет быть выбран.
cos xdx
4
dx
1 4 cos x
cos xdx
cos x sin 2 xdx
3
dx
tg 3 x
11. Пример
• Укажите, какой подход при интегрированииможет быть выбран.
cos xdx
4
1
cos x (1 cos 2 x)
2
2
cos xdx
dx
1 4 cos x
t sin x
x
tg t
2
3
t tg x
sin cos
cos x sin 2 xdx
dx
tg 3 x
1
(sin( ) sin( ))
2
t tg x
12. Пример
dxsin xdx
d (cos x)
1 1 cos x
sin x sin 2 x 1 cos 2 x 2 ln 1 cos x C
1 cos x
ln
C
1 cos x
x
tg t
2
2
dx
dt
2
1 t
2t
sin x
1 t2
dx
2dt
dt
x
sin x 2 2t t ln | tg 2 | C
(1 t )
1 t 2
13.
dxx
cos x ln tg 2 4 C
x
tg t
2
2
dx
dt
2
1 t
tg tg
tg ( )
1 tg tg
1 t 2
cos x
2
1 t
2
dx
1 t
2
dt
cos x 2 (1 t 2 ) 1 t 2 dt ln 1 t C
(1 t )
1 t 2
x
x
1 tg
tg tg
x
2
4
2
ln
C ln
C ln tg C
x
x
2 4
1 tg
1 tg tg
2
2
4
14. 4. Неберущиеся интегралы
Интегральное исчисление4. Неберущиеся интегралы
15.
• Если интеграл не выражается черезконечное число элементарных функций, то
такой интеграл называют «неберущимся»,
т.е. его нельзя найти («взять») в виде
элементарной функции.
16.
• Примеры неберущихся интегралов(неэлементарные специальные функции,
которые затабулированы):












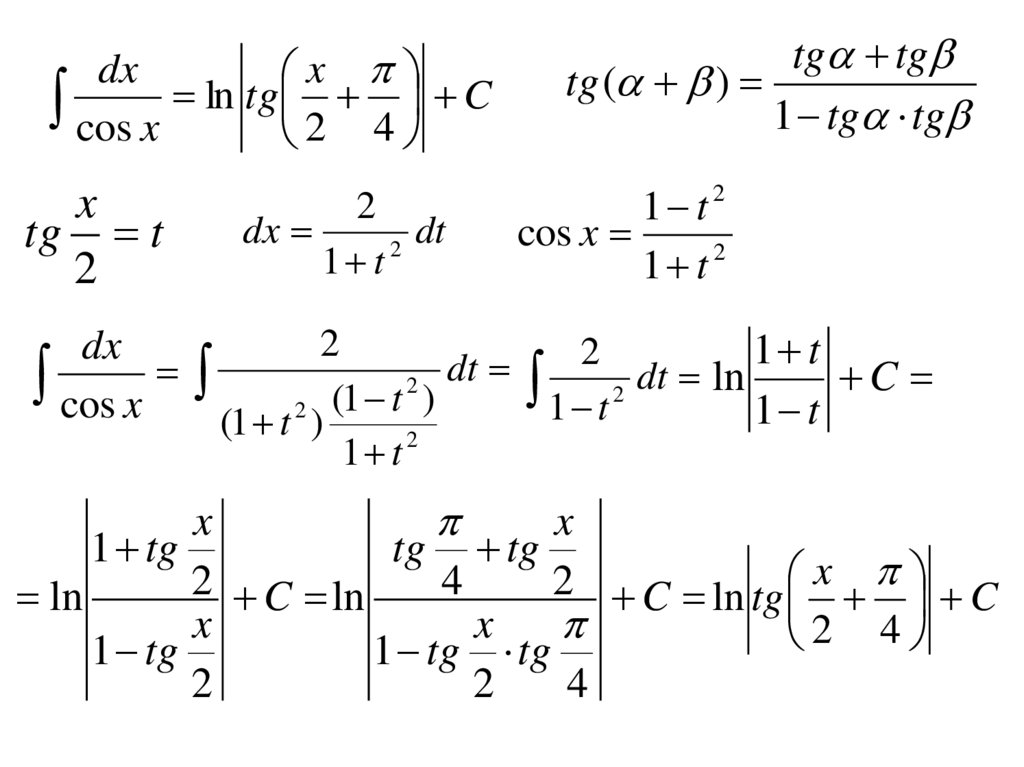



 Математика
Математика








