Похожие презентации:
Общие теоремы динамики точки
1.
Комплект слайд-лекций для техническихспециальностей университета
2.
доктор физико-математических наук,профессор Отделения машиностроения
Инженерной школы новых производственных технологий
Томского политехнического университета
3.
Общие теоремы динамики точки4. Теорема об изменении количества движения точки
Количеством движения точки называетсявекторная величина:
Q mV
(1)
5.
Представим основной закон динамики в виде:d mV
F
dt
(2)
6.
Представим основной закон динамики в виде:или
d mV
F
dt
d mV F dt
(2)
7.
Представим основной закон динамики в виде:или
d mV
F
dt
d mV F dt
d mV dS
(2)
dS F dt - элементарный импульс силы
(3)
8.
Интегрируем уравнение (3):d
m
V
d
S
C
9.
Интегрируем уравнение (3):d
m
V
d
S
C
mV mV0 S
(4)
10.
Интегрируем уравнение (3):d
m
V
d
S
C
mV mV0 S
(4)
Изменение количества движения точки за некоторый
промежуток времени равняется импульсу действующих
на точку сил за тот же промежуток времени.
11. Пример:
Точка массой m 1кг , двигаясь прямолинейнопод действием постоянной силы F , изменила
свою скорость на V 2 м / с в течение
промежутка времени
t 0,5c.
Определить силу F.
12. Решение:
m V F t13.
Решение:m V F t
V
2
F m
1 4H
t
0,5
14.
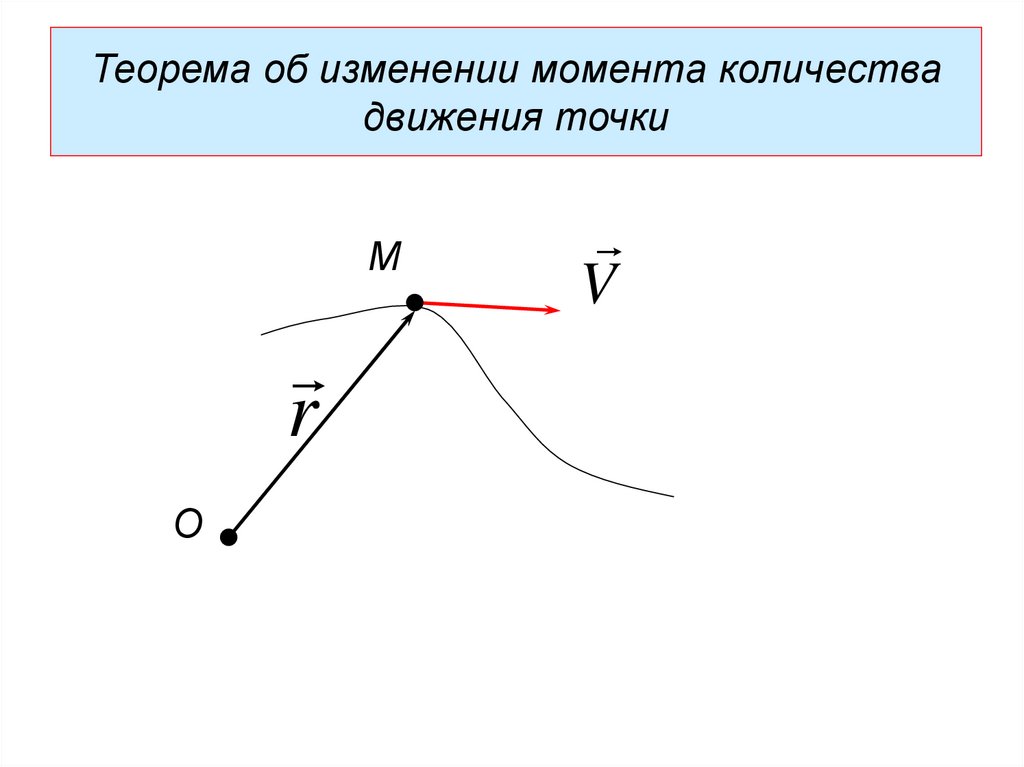
Теорема об изменении момента количествадвижения точки
М
r
О
V
15.
Умножим уравнение (2) слева на радиус-векторd mV
r
r F
dt
r
16.
Умножим уравнение (2) слева на радиус-вектор rd mV
r
r F
dt
или
d r mV
M0
dt
G0 r mV
(5)
-момент количества движения
(кинетический момент)
точки относительно центра О
17.
Замечание:d mV
d r mV
dr
mV r
dt
dt
dt
d mV
d mV
V mV r
r
dt
dt
18.
dG0M0
dt
(6)
19.
dG0M0
dt
(6)
Производная по времени момента количества
движения точки относительно какого-либо
центра равна моменту действующих на точку
сил относительно того же центра.
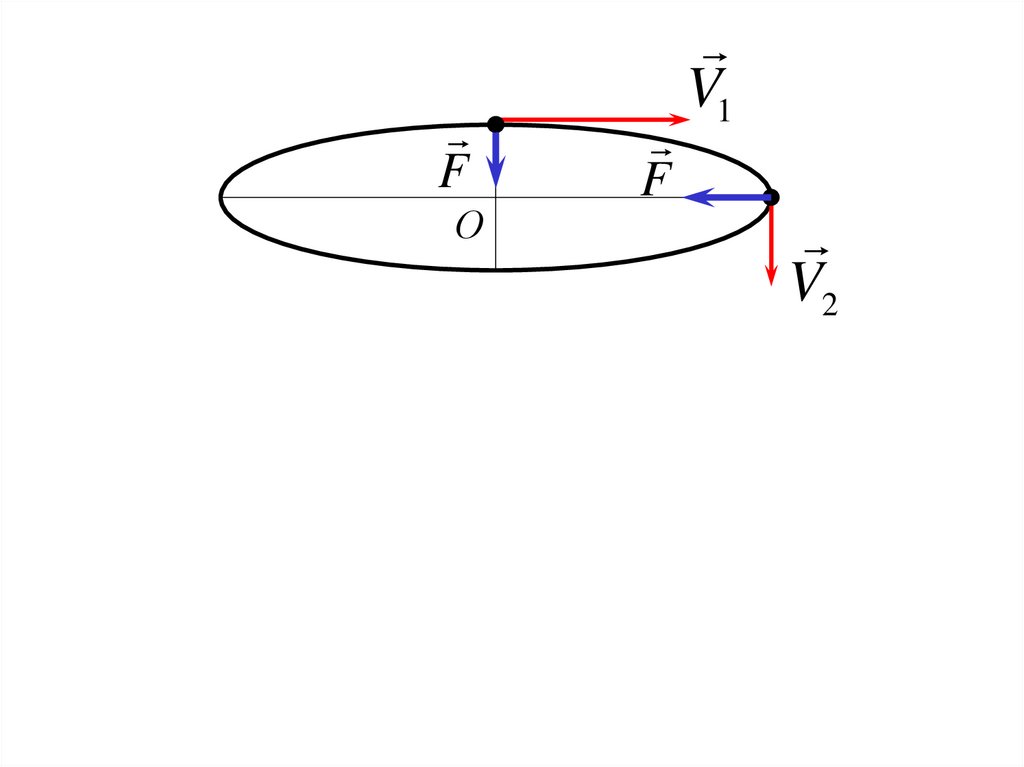
20. Пример:
Точка М движется вокруг неподвижного центрапо эллипсу под действием силы притяжения к
этому центру. Найти скорость точки в наиболее
удаленной от центра точке траектории, если
ее скорость в наиболее близком к нему положении
V 30 м / с , а наибольший радиус в 5 раз больше
наименьшего.
21.
FО
F
V1
V2
22.
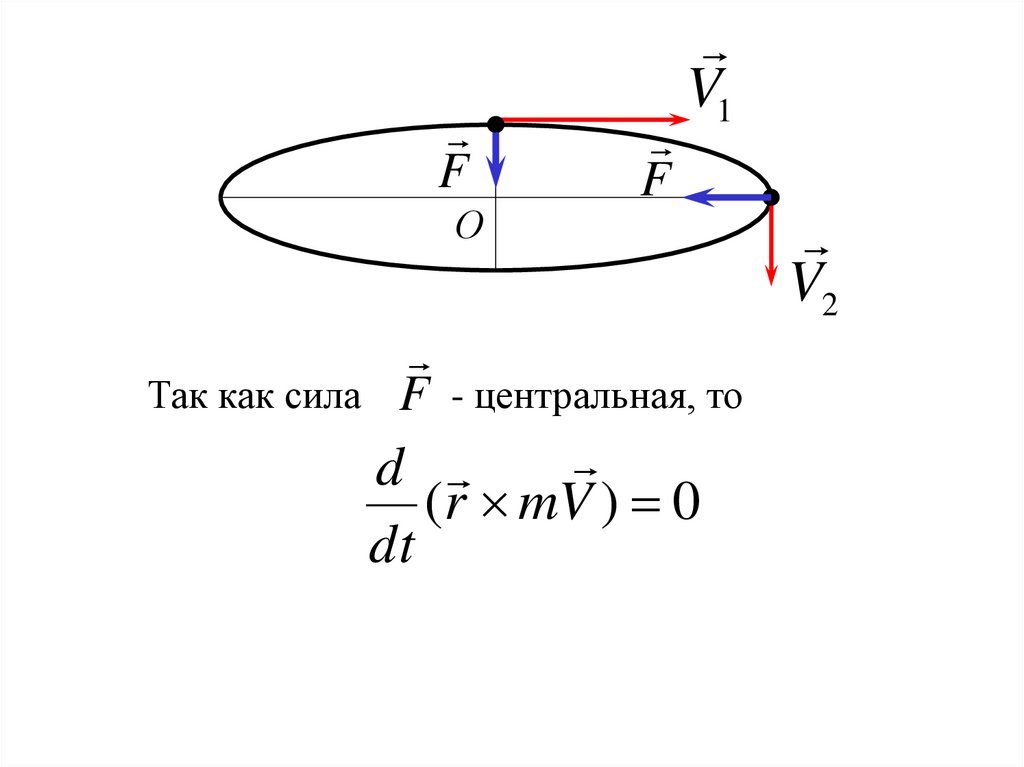
FО
Так как сила
F
V1
F - центральная, то
d
(r mV ) 0
dt
V2
23.
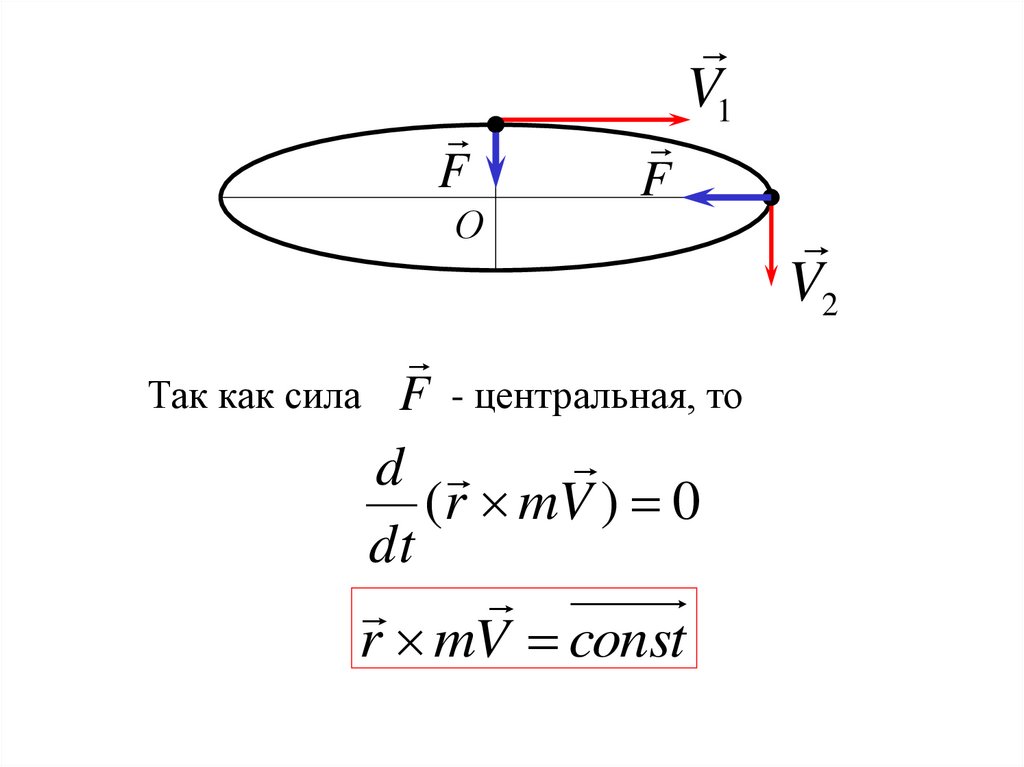
FО
Так как сила
F
V1
F - центральная, то
d
(r mV ) 0
dt
r mV const
V2
24.
Следовательноr1mV1 r2 mV2
r1V1 30
V2
6м / с
r2
5
25. Теорема об изменении кинетической энергии точки
Кинетической энергией точки называется скалярнаявеличина
mV 2
T
2
(7)
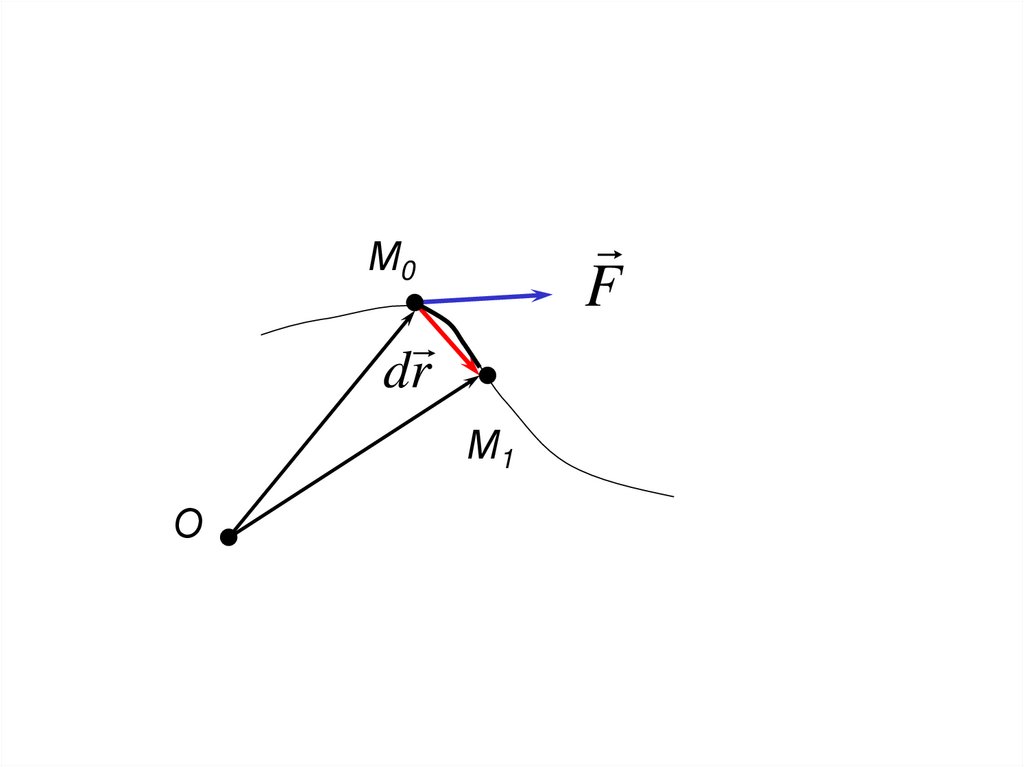
26.
FМ0
dr
М1
О
27.
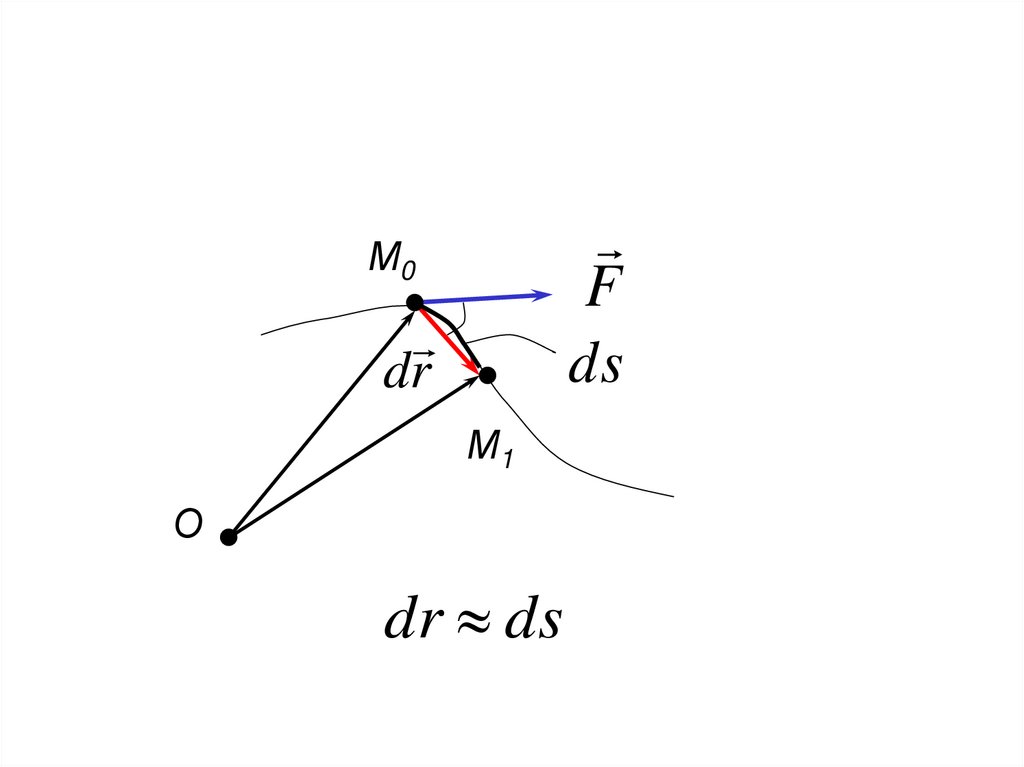
Fds
М0
dr
М1
О
dr ds
28.
Элементарной работой силы, совершенной наперемещении dr называется скалярное
произведение
d A F dr
(8)
d A - не всегда является полным дифференциалом
29.
Элементарной работой силы, совершенной наперемещении dr называется скалярное
произведение
d A F dr
(8)
d A - не всегда является полным дифференциалом
d A F ds cos F , dr
(9)
30.
Проекция силы на касательную:F F cos F , dr
31.
Проекция силы на касательную:F F cos F , dr
Работа силы на конечном перемещении по
кривой М0М1
AM 0 M1
F
ds
M 0 M1
(10)
32.
Умножим (2) скалярно на вектор скорости:d mV
V
F V
dt
33.
Умножим (2) скалярно на вектор скорости:d mV
V
F V
dt
d mV
F V
dt 2
2
или
34.
Умножим (2) скалярно на вектор скорости:d mV
V
F V
dt
d mV
F V
dt 2
2
d mV dr
F
dt 2
dt
2
или
35.
mVF dr
d
2
2
dT d A
36.
mVF dr
d
2
2
dT d A
(11)
Интегральная форма:
T T0 A
(12)
37.
mVF dr
d
2
2
dT d A
(11)
Интегральная форма:
T T0 A
(12)
Изменение кинетической энергии точки на
некотором перемещении равно работе
действующих на точку сил на том же перемещении.
38.
Если работа силы представляет собой полныйдифференциал некоторой функции:
dA dП
39.
Если работа силы представляет собой полныйдифференциал некоторой функции:
dA dП
то из (11) следует
dT dП
40.
Если работа силы представляет собой полныйдифференциал некоторой функции:
dA dП
то из (11) следует
dT dП
В результате интегрирования получим
закон сохранения энергии:
T П Е
(13)
П- потенциальная энергия точки, Е- полная энергия
41.
Пример: вертикальное падение тела42.
2mV
mgh E
2
2
mVmax
mghmax
2
Vmax 2ghmax
43.
Контрольные вопросы:1. Дайте определение понятию «импульс силы».
2. Точка движется по окружности. Как направлен ее
момент количества движения?
3. Дайте определение понятию «работа силы».
4. Приведите примеры консервативных и
неконсервативных сил.
44. ТЕСТОВЫЕ ЗАДАНИЯ
Для самоконтроля знаний рекомендуетсявыполнить тестовые задания из
Сборника коротких задач по теоретической
механике. Под ред. Кепе О.Э.
С. 230, 242, 250
Рекомендованные учебники и учебные пособия выложены в
информационном модуле
45.
После просмотра и конспектирования слайд-лекциинеобходимо прочитать указанные страницы
учебников и дополнить конспект наиболее важными
сведениями
Тарг С.М. Краткий курс теоретической механики: Учеб. для
втузов.- 10-е изд. – М: ВШ, 1986. С. 201-219.
Рекомендованные учебники и учебные пособия выложены в
информационном модуле







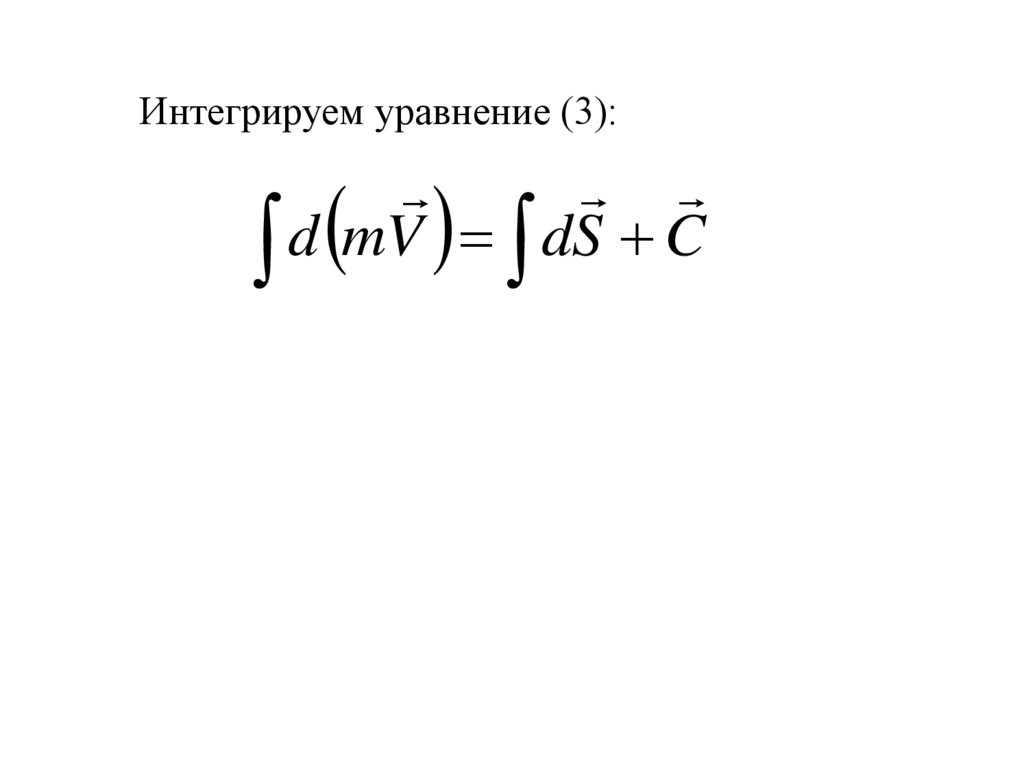







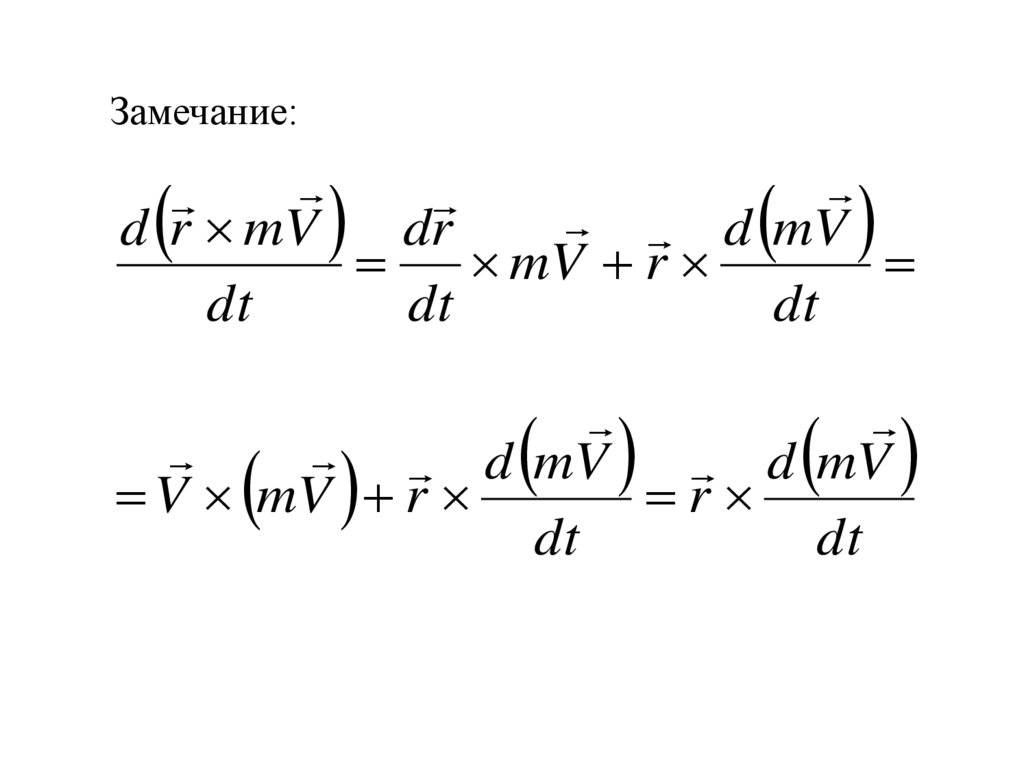
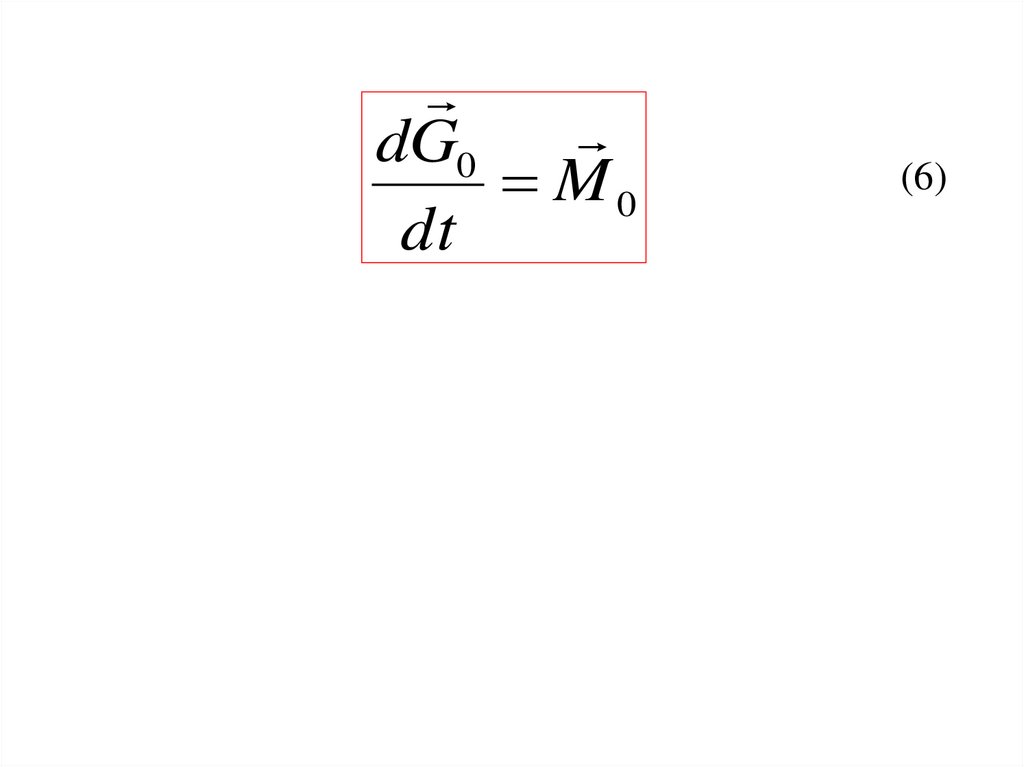











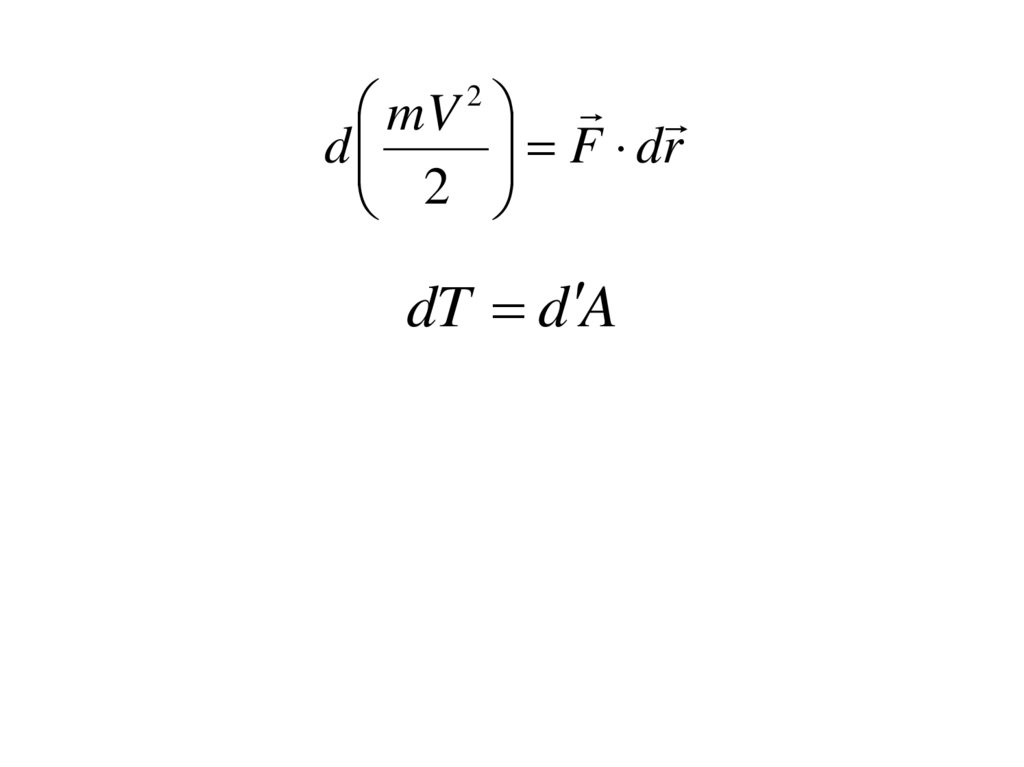






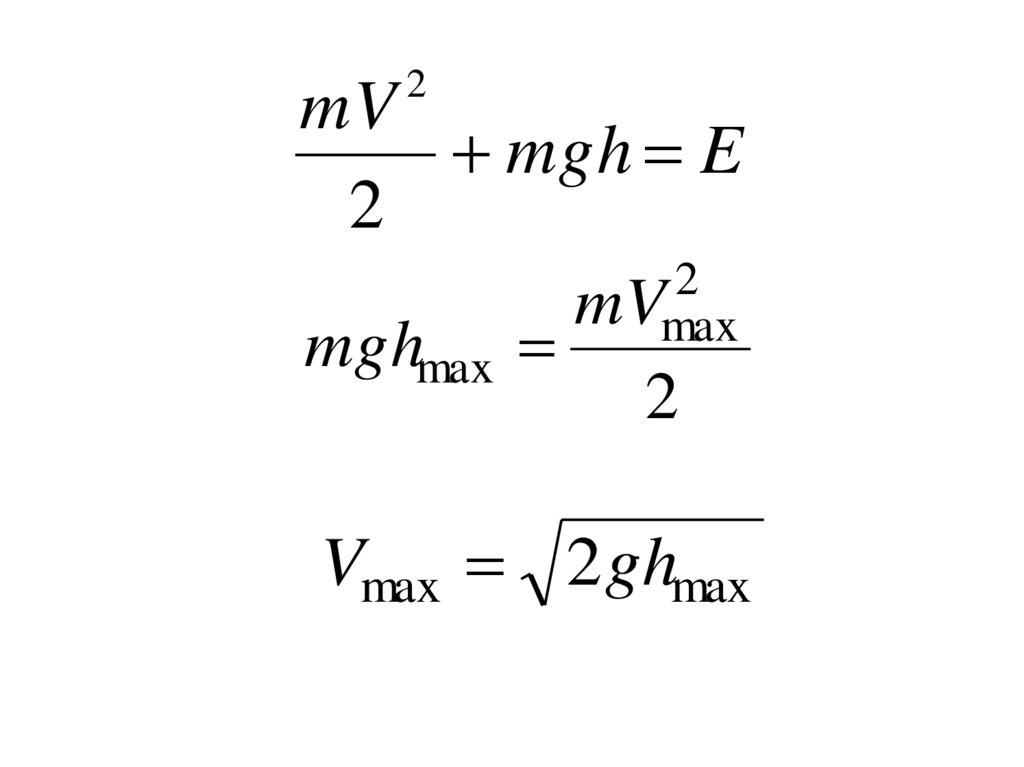



 Физика
Физика








