Похожие презентации:
Lektsia_8_Proizvedenie_vektorov
1. Векторная алгебра
Скалярное произведение двух ненулевыхвекторов
Векторное произведение двух ненулевых
векторов
Смешанное произведение трех ненулевых
векторов
Двойное векторное произведение векторов
2. Скалярное произведение
Пусть материальная точка под действием силы Fперемещается из положения M1 в положение M 2
Как известно из физики, работа силы F по
перемещению точки М 1 определяется по
формуле:
A F S cos
M1
F
Таким образом, двум векторам:
силе и перемещению оказался
сопоставлен скаляр – работа.
M2
F
Этот
скаляр А и
называется скалярным
произведением
силы
Скалярным
произведением
двух векторов
называется
число,
наравное
перемещение
произведению
модулей этих векторов на косинус угла между
S
ними.
3. Скалярное произведение векторов
Скалярное произведение двух векторов a и b обозначается:a ba ; bcos
a b
или
Если векторы a и b ненулевые:
a b 0
ПР
cos
a a b
a b a bПР
cos
b aПР
b
ab
a a a a cos 0o a 2 a 2
ПРb a
Критерий
Скалярный квадрат
ортогональности
вектора
равен
двух
векторов
квадрату
его модуля
Законы скалярного произведения
1) a b b a
2)
(a b ) c a c b c
3) (a b ) ( a ) b a ( b )
a b
4.
Скалярное произведение векторовНайти длину вектора а = 3с - 2d при условии,
что
c 5,
d 4, c , d 600
В треугольнике АВС угол при вершине А равен 120
градусов, а длина стороны АС в три раза больше
расстояния между вершинами А и В. Найти острый
угол между стороной ВС и медианой АМ
треугольника.
5. Скалярное произведение векторов Вычисление в координатах
Для координатных ортов декартовой системы координатсправедливо:
i i j j k k 1
i j i k j k 0
Пусть в декартовой прямоугольной системе координат заданы
векторы:
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
Найдем скалярное произведение:
a b x1 i y1 j z1 k x2 i y 2 j z2 k
z y 0
j k x z k0 i y z 0j k z z k1
x1x2 i12 y 1x2 i0 j z1x2 i 0 k x1y 2 j0 i y1y 2 j12
2
1
2
1 2
1 2
x1 x2x1 yx12 y2y 1 zy1 2 z 2 z 1 0 z2
a b
1 2
Критерий
Скалярное произведение
ортогональности
в
в координатах
координатах
6. Скалярное произведение векторов Вычисление в координатах
Из формулы скалярного произведения векторов следует формуладля нахождения угла между векторами:
a b
cos
a b
x1 x 2 y 1 y 2 z1 z2
x12 y 12 z12 x 22 y 22 z22
Найти косинус угола между векторами:
a b 1 6 2 4 3 2 8
a i 2 j 3k
b 6i 4 j 2k
a 12 22 3 2 14
b 62 42 2 56 2 14
8
2
cos
14 2 14 7
2
7.
Скалярное произведение векторовВычисление в координатах
Найти значение параметра t, при котором векторы
a t;1 t;7 b t 1;2; 2
, заданные своими координатами в
ортонормированном базисе, ортогональны.
8. Векторное произведение векторов
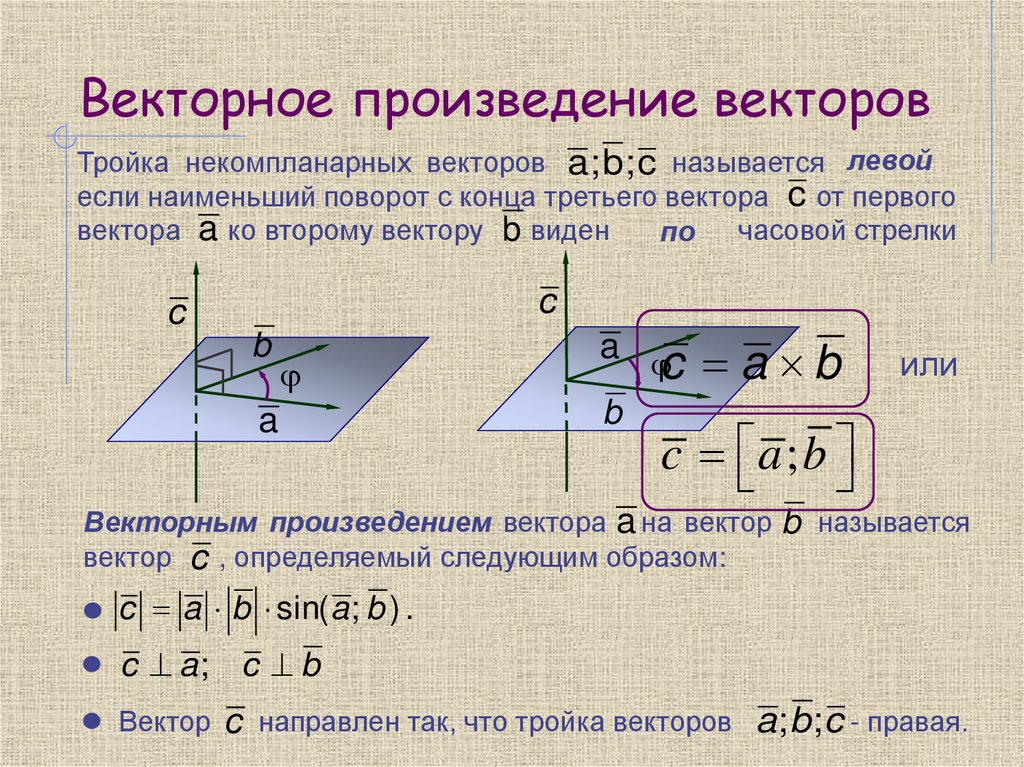
левойТройка некомпланарных векторов a; b ; c называется правой
если наименьший поворот с конца третьего вектора c от первого
вектора a ко второму вектору b виден против
часовой стрелки
по
c
c
b
a
a
c a b
b
или
c a ; b
Векторным произведением вектора a на вектор b называется
вектор c , определяемый следующим образом:
c a b sin( a ; b ) .
c a; c b
Вектор c направлен так, что тройка векторов
a; b ; c - правая.
9. Векторное произведение векторов Геометрические свойства
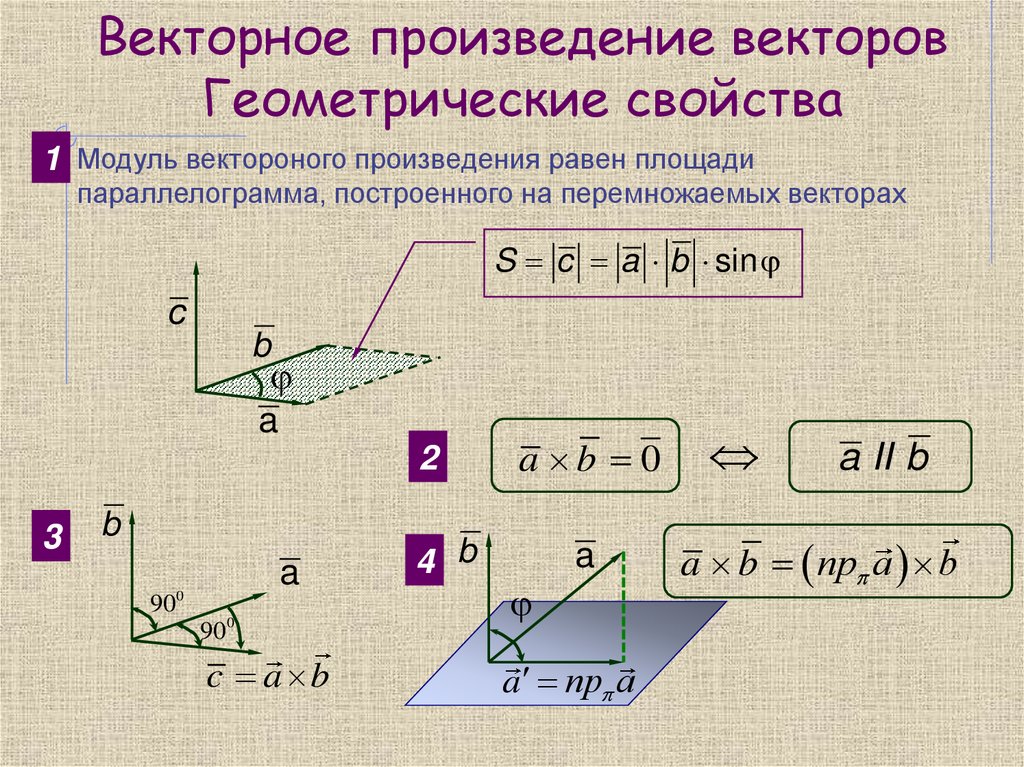
1 Модуль вектороного произведения равен площадипараллелограмма, построенного на перемножаемых векторах
S c a b sin
c
b
a
3
b
a
900
90
0
c a b
2
a b 0
4 b
a
a пр a
a II b
a b пр a b
10.
Векторное произведение векторовАлгебраические свойства
1) a b b a
2) a b c
a b a c
3) (a b ) ( a ) b a ( b )
4) a a 0
Найти площадь параллелограмма, построенного на
векторах а = 3с -2d и b = c + d при условии, что
c 1
d 4 c, d
6
11. Векторное произведение векторов
Для координатных ортов декартовой системы координатсправедливо: i i j j k k 0
k 900 j0 1
j i k k i - j sin
i j k sin 90 0 1
j k i sin 90 1
k j i
j k i
k i; k j i
i j; i k
; j i
i k j i ; j ;jk kправая
k i j
тройка
j ; k ; i правая тройка
k ; i ; j правая тройка
произведение двух разноименных
i j k
k
i
+
j
Векторное
ортов, следующих друг за другом в направлении
положительного
обхода
окружности,
равно
Пусть
в
декартовой
прямоугольной
системе
заданы
третьему
орту
со
знаком
плюс,координат
в
векторы:
противоположном же случае - знаком минус.
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
Найдем векторное произведение:
12. Векторное произведение векторов
x x i 0 i y xj ki z x k j i x y i
k j
y y j0 j z y k i j x z i jk
y z ji k z z 0k k
a b x1 i y1 j z1 k x2 i y 2 j z2 k
1
1
2
1
2
1
1
2
2
1
2
1
1
2
1
2
2
2
y1x2 k z1x2 j x1y 2 k z1y 2 i x1z2 j y1z2 i
y1
z1
x1
z1
x1
y1
y2
z2
x2
z2
x2
y2
y1z2 z1y 2 i x1z2 z1x2 j x1y 2 y1x2 k
i
j
k
a b x1 y 1 z1
x 2 y 2 z2
13. Векторное произведение векторов
Найти векторное произведение векторов:a 2i 3 j k
i
j
b 3i j 4k
k
a b 2 3 1
3 1 4
3
1
1 4
i
2
1
3
4
j
2
3
3
1
k
12 1 i 8 3 j 2 9 k 11i 5 j 7k
14. Векторное произведение векторов
Найти площадь треугольника с вершинами:A 2; 3; 1
B 5; 6; 3
C 7; 1; 10
В
Найдем координаты векторов:
AB 5 2; 6 3; 3 1 3; 3; 2
AC 7 2; 1 3; 10 1 5; 2; 9
S
А
1
a b
2
i
j
k
a b 3 3 2 31i 17 j 21k
5 2 9
1
S
312 ( 17)2 ( 21)2
2
1
1691 20, 6
2
С
15. Смешанное произведение векторов
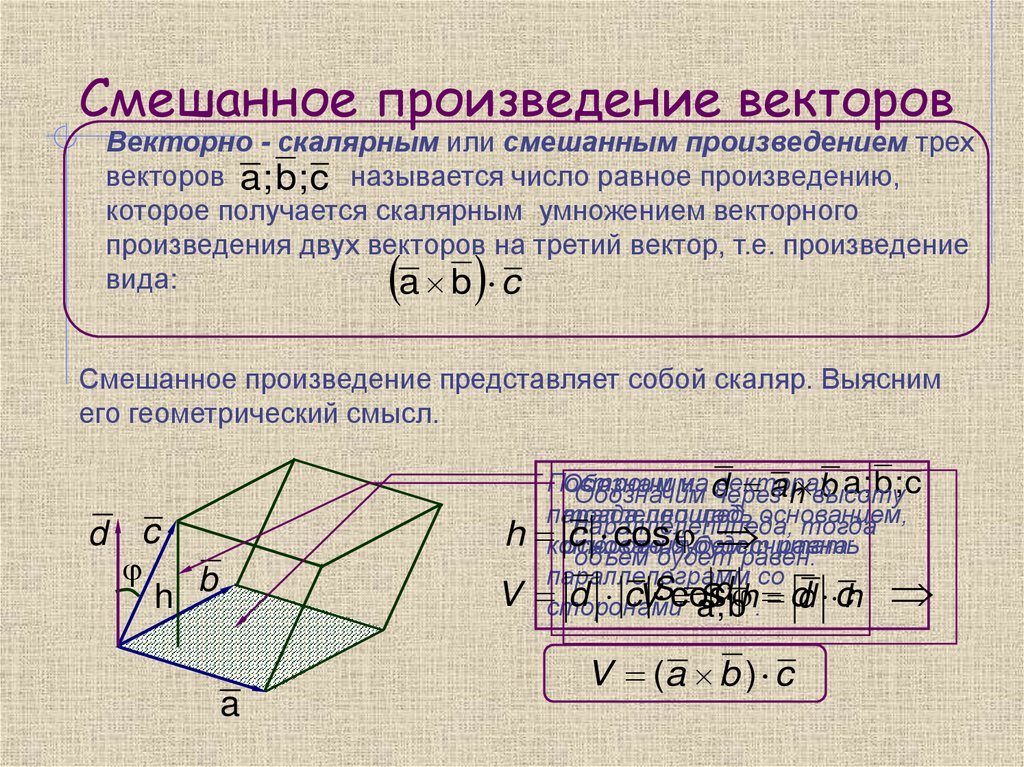
Векторно - скалярным или смешанным произведением трехвекторов a; b ; c называется число равное произведению,
которое получается скалярным умножением векторного
произведения двух векторов на третий вектор, т.е. произведение
вида:
a b c
Смешанное произведение представляет собой скаляр. Выясним
его геометрический смысл.
Построим
на d
векторах
Обозначим:
, ; b; c
a h высоту
ba
Обозначим
через
параллелепипед,
тогда
площадь основанием,
параллелепипеда,
тогда
h которого
c
cos
будем
считать
основания
будет
равна:
объем будет
равен:
параллелограмм со
V сторонами
d cVS cos
a
Sd; b h. dd ch
d c
h b
a
V (a b ) c
16. Смешанное произведение векторов
Смешанное произведение трех векторов равно объемупараллелепипеда, построенного на этих векторах в том случае,
если векторы a; b ; c образуют правую тройку векторов (как в
предыдущем примере).
В случае, если векторы образуют левую тройку, то смешанное
произведение равно объему параллелепипеда, взятому со знаком
«-»:
a b c V
Таким образом, объем параллелепипеда, построенного на трех
векторах, всегда равен абсолютной величине их смешанного
произведения:
V a b c
Замечание:
abc 0
a ; b ; c компланарны
17. Смешанное произведение векторов
Законы смешанного произведения1) Сочетательный закон следует из геометрического
смысла смешанного произведения:
V a b c
a b c a (b c )
V a (b c )
Учитывая сочетательный закон, смешанное произведение
обозначают: (a ; b ; c ) или a b c .
2) Закон круговой переместительности:
a b c b c a c a b a c b c b a b a c
c
b
a
При перестановке множителей не нарушающей их кругового
порядка, смешанное произведение не меняется, при
перестановке же множителей, нарушающей круговой
порядок, смешанное произведение меняет свой знак
18. Смешанное произведение векторов
3) Распределительный законa a b c a b c a b c
1
2
1
2
В частности, смешанное произведение равно нулю, если в нем
два множителя одинаковы: a a c 0
Пусть в декартовой прямоугольной системе координат заданы
векторы:
a x1 i y1 j z1 k
b x2 i y 2 j z2 k
c x3 i y 3 j z3 k
19. Смешанное произведение векторов
ij
k
y2
b c x 2 y 2 z2
y3
x 3 y 3 z3
a (b c )
y2
z2
y3
z3
x1
z2
z3
i
x2
z2
x3
z3
x1 y 1 z1
a b c x 2 y 2 z2
x3 y 3 z3
x2
z2
j
x2
y2
x3
z3
x3
y3
x2
y2
y1
x3
y3
z1
k
20. Смешанное произведение векторов
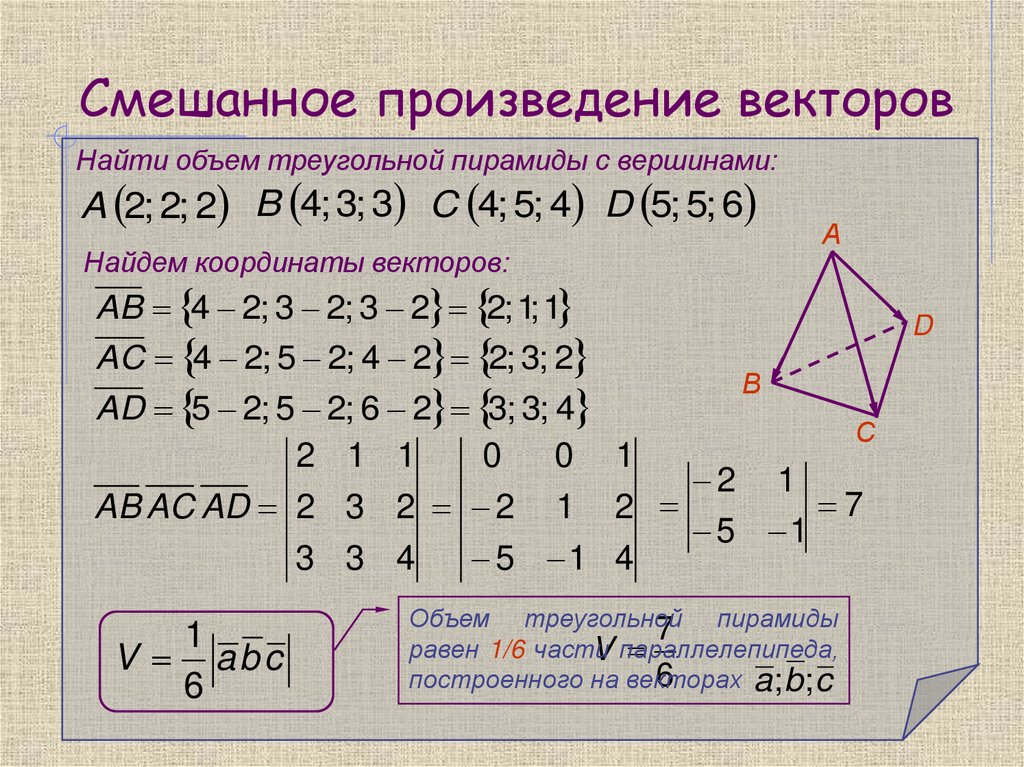
Найти объем треугольной пирамиды с вершинами:A 2; 2; 2 B 4; 3; 3 C 4; 5; 4 D 5; 5; 6
А
Найдем координаты векторов:
AB 4 2; 3 2; 3 2 2; 1; 1
D
AC 4 2; 5 2; 4 2 2; 3; 2
AD 5 2; 5 2; 6 2 3; 3; 4
2 1 1
0
0 1
1
V abc
6
С
2
1
7
1 2
5 1
5 1 4
AB AC AD 2 3 2 2
3 3 4
В
Объем треугольной
7 пирамиды
равен 1/6 части
V параллелепипеда,
6
построенного на векторах
a; b ; c
21.
Двойное векторное произведениетрех векторов
Двойным векторным произведением трех векторов
называется
вектор
равный
векторному
произведению вектора
на векторное
а
произведение векторов b и c .Обозначается
a b c
Свойства двойного векторного произведения
трех векторов
1. a b c b a c c a b формула Лагранжа
2. a, b , c b , c , a c , a, b 0 тождество Якоби
22.
Свойства двойного векторного произведениятрех векторов
3.
b
a b
a
4.
2
a
1
a , b , a , a 0
a
2
d b a c c a b
T
a xa ya za
T
T
b xb yb zb
T
, где
c xc yc zc координатные
T
столбцы данных векторов в ортонормированном базисе.
Замечание.
Формула Лагранжа доказывается, применяя формулы
вычисления скалярного и векторного произведений в
ортонормированном базисе.
23.
Правило для запоминания формулы Лагранжа.Двойное произведение равно среднему вектору,
умноженному на скалярное произведение двух других,
минус крайний вектор скобки, умноженный на скалярное
произведение двух остальных.
Замечание.
Второе свойство следует из первого, если сделать
циклическую перестановку векторов
b , c , a a , b c c , b a
a b c b a c c a b
c , a , b c , b a c , a b
а затем сложить эти равенства вместе с исходным
(учитывая коммутативность скалярного произведения)
24.
Замечание.Третье свойство следует из первого, если положить a c
и представляет разложение данного вектора b на две
компоненты, из которых одна параллельна, а другая
перпендикулярна к заданному вектору a
В
AB прa b
b
А
В’
a
B B b a
a b
a
2
a
1
a , b , a ,
a
2
Даны векторы
Найти двойное векторное произведение a b c .




















 Математика
Математика








