ЛОГИКА_ЛИН_АЛГЕБРА_И_АНАЛ_ГЕОМЕТРИЯ_стерил_3

1.

СПИСОК ВОПРОСОВ К ПЕРВОМУ РУБЕЖНОМУ КОНТРОЛЮ 2025-2026 уч. год
1.*Опр. высказывания, логической формулы и булевой функции.Пр. 2.Опр. обратной,
противоположной теорем и метода доказательства от противного.Пр. 3.*Опр. предика
та и кванторов общности и существования. Пр. 4.*Опр. матрицы, транспонированной
матрицы и алгебраического дополнения элемента матрицы. Пр. 5.Опр. суммы матриц
произведения матрицы на число и произведения матриц. Пр. 6.* Опр. определителя,
минора и ранга матрицы. Пр. 7.*Опр. СЛАУ, совместной и определенной СЛАУ. Пр.
8.* Опр. векторного пространства (ВП). Пр. 9. Опр. декартова произведения
множеств и векторных пространств. Пр. 10. Опр. линейной комбинации элементов и
базиса в ВП. Пр. 11.* Опр. скалярного произведения и нормы в ВП. Пр. 12.* Опр.
отображения множеств, линейного и полилинейного отображений ВП. Пр. 13.* Опр.
n-мерных евклидова пространства. Пр.
14.* Опр. ДСК и полярной системы координат. Пр. 15. Опр. ортонормированного
базиса и прямоугольной ДСК. Пр. 16.* Опр. компонент элемента, радиуса-вектора и
координат точки. 17. Опр. сферической и цилиндрической систем координат. Связь с
декартовыми.
18. Опр. проекции вектора на ось и ее свойства. 19.* Опр. правой тройки и вектор
ного произведения. 20. Физические смыслы скалярного, векторного произведений.
21. Опр. смешанного произведения и геом. смыслы модулей векторного и смешан
ного произведений. 22.* Опр. плоскости и два аналитических способа ее задания.
23. Опр. прямой и два способа ее задания в пространстве. 24.* Опр. кривой второго
порядка и эллипса. Уравнение. 25. Опр. гиперболы и параболы. Уравнение. 26. Опр.
алгебраической поверхности второго порядка и конуса. График. 27. Опр. и рисунки
эллипсоида, одно- и двуполостных гиперболоидов. 28. Опр. и рисунки
эллиптического, гиперболического параболоидов и конуса.

2.

3.

§ 2.1 Системы линейных алгебраических
уравнений (СЛАУ). Матрицы. Определители.
Матрицы
Матрица размера m n - совокупность чисел, расположенных
в виде таблицы из m строк и n столбцов. ЛЕКЦИЯ 2 13.09.18
a11 ... a1n a11 ... a1n
Обозначение A ... ... ... ... ... ... aij aij .
a
m1 ... amn am1 ... amn
Матрицы A (aij ), B (bij ) называются равными A B ,
если они имеют одинаковые размеры и i j aij bij .
ЗАМЕЧАНИЕ Понятие матрицы впервые появилось в середине
XIX века в работах Уильяма Гамильтона и Артура Кэли.
Термин «матрица» (от matrix - лат. матка животного) ввел Джеймс
Сильвестр в 1850 г.

4.

Матрица квадратная, если m=n.
- главная
диагональ
- побочная
диагональ
Квадратная матрица единичная, если все элементы главной
диагонали равны 1, а остальные элементы равны 0.
1 0 0
1 0
,...
,
0
1
0
Пр. E (1),
0
1
0 0 1
Квадратная матрица нулевая, если все ее элементы равны нулю.
0 0 0 0 0 0
Пр. E (0), (0 0), , ,
,...
0 0 0 0 0 0

5.

Сумма двух матриц A (aij ), B (bij ) размера m n это
матрица, которая обозначается и вычисляется по формуле
a11 b11 ... a1n b1n
A B : (aij bij ) ............................
a b ... a b
mn
mn
m1 m1
Пр. 1 1 0 .
1 1 0
Произведение матрицы A (aij ) на число это матрица вида
a11 ... a1n
A : ( aij ) ..................
a ... a
mn
m1
1
1
0
1
2
2
Пр. 2
1
1 1 2
2
4
0 1
; 1 0 : ( 1) 1 0 1 0 .
0 1
0 1 0 1
2 4

6.

Произведение матрицы A (aij ) размера m p на матрицу
B (bij ) размера p n - это матрица A B : (ci j ) размера m n ,
элементы которой вычисляются по правилу
p
cij : ai1b1 j ... aip bpj aik bkj
k 1
1 0
1 0 0
0 1
Пр. A
,
B
0
1
0
0 0
2 3
1 0 0
1 0
0 1 0
AB
,
BA
0
1
0 0 0
2 2
3 2
3 3
Обратная к квадратной матрице A (ai j ) размера n n квадратная матрица A 1 (bi j ) размера n n со свойством
AA 1 A 1 A E .
ЛЕКЦИЯ 2 23.09.19

7.

Определитель
Определитель (детерминант) первого порядка квадратной
матрицы A (a11 ) размера 1 1 - число, обозначаемое и
вычисляемое по формуле
det A a11 : a11
Пример
det( 10) 10 10 .
Determinacio – лат. определять.

8.

Определитель n-го порядка квадратной матрицы A (aij )
размера n n - число, обозначаемое
a11 ... a1n
det A ... ... ... ,
an1 ... ann
которое находится по формуле
n
det( A) : ai1 ( 1) M i1 ... ai n ( 1) M i n ai k ( 1)i k M i k ,
i 1
i n
k 1
где M i k - определитель (n-1)-го порядка матрицы, которая получается вычеркиванием из матрицы A i-той строки и k-го столбца.
ЗАМЕЧАНИЕ Данная формула вычисления - разложение определителя по i- ой строке.
Формула разложения по j-ому столбцу:
n
det A ak j ( 1)k j M k j a1 j ( 1)1 j M1 j ... an j ( 1) n j M n j .
k 1

9.

Пример 1
a11 a12
2
3
a11 1 a22 a12 1 a21 a11a22 a12 a21
a21 a22
1 0 1
Пример 2 Вычислим определитель 0 2 1
1 3 0
разложением по второй строке и по третьему столбцу.
1 0 1
1
1
0
3 0
4 1
5 1
0 2 1 0 1
2 1
1 1
3 0
1 0
1 3
1 3 0
0 2 1 3 1
1 0 1
2
0
0
4 0
5 1
6 1
0 2 1 1 1
1 1
0 1
1 3
1 3
0 2
1 3 0
2 3 1

10.

ТЕОРЕМА 2.1 (свойства определителей)
1) Если в определителе поменялись местами две строки (два
столбца), то новый определитель будет отличаться от
исходного только знаком.
2) Если элементы одной строки (или столбца) умножить на одно и
тоже число , то полученный новый определитель будет в
раз больше исходного.
3) Если к одной строке (столбцу) прибавить поэлементно
другую строку (столбец), то полученный новый определитель
совпадет с исходным.
4) Пусть два определителя одинакового порядка различаются
только одной строкой (столбцом). Тогда их сумма совпадает с
определителем, у которого соответствующая строка (столбец)
есть сумма строк (столбцов) слагаемых определителей.

11.

◄ 1) Ограничимся случаем n =2.
a21
a11
a22
a
a21a12 a11a22 a11a22 a12 a21 11
a12
a21
a12
.
a22
2) По определению определителя
a11 ... a1n
a21
...
an1
...
...
...
a11
a2 n
a
a11 ( 1)1 1 M11 ... a1n ( 1)1 n M1n 21
...
...
ann
an1
... a1n
... a2 n
.
... ...
... ann
3) Пусть n=2 и к первой строке прибавлена вторая. Тогда
a11 a21 a12 a22
a
a
a11a22 a21a22 a21a12 a21a22 a11a22 a12a21 11 12 .
a21
a22
a21 a22
1 0
1 3
1 5
1 8
4) (пример)
17 .
2 1
2 2
2 0
2 1
a11 ... a1n
... a1 n
a11
a21 ... a2 n a21 ... a2 n
)( 1)1 1 M11 ... (a1n a1 n )( 1)1 n M1n
(a11 a11
... ... ...
... ... ...
an1 ... ann an1 ... ann
... a1n a1 n
a11 a11
a21
...
an1
...
...
...
a2 n
...
ann
.%

12.

Минор порядка k матрицы A - определитель матрицы,
элементы которой стоят на пересечении каких-либо k строк и
k столбцов матрицы A.
1 0 2
Пр.1 Матрица
имеет 3 минора порядка 2,
2 3 4
6 миноров порядка 1 и не имеет миноров порядка 3.
4 6
1 2
1 4 6
Пр.2 0 1 1 1 det 0 1 1 2 rangA 3 .
0 0 2 1
0 2 1
Ранг матрицы - самый большой порядок у не равных нулю
миноров этой матрицы.
1 1 1
1 1 1
Пр. A 2 2 2 det A 2 2 2 0 rangA 3.
3 3 3
3 3 3
1 1
1 1
2 2
0;
0;
0 rangA 2.
2 2
3 3
3 3
1 1 rangA 1

13.

Квадратная матрица A невырожденная, если rang A n , то
есть когда det A 0 . ЛЕКЦИЯ 3 9.09.16
a11 ... am1
Матрица AT A : ... ... ... называется транспонированной
a
...
a
mn
1n
a11 ... a1n
к матрице A ... ... ... .
a
...
a
mn
m1
2
Пр. A AT 2 1 . ЛЕКЦИЯ 2 12.09.17
1
Ai j : ( 1)i j M ij - алгебраическое дополнение элемента aij
матрицы A. ЛЕКЦИЯ 3 14.09.15
( Ai j )T - присоединенная матрица к матрице A.

14.

ЗАМЕЧАНИЕ Если матрица A не вырождена, то существует
обратная матрица A 1 , которая вычисляется по формуле
1
A
( Aij )T ,
det A
1
где Ai j : ( 1)i j M ij
a22
T
Пусть n 2 ( Aij )
a12
◄
a21 a22 a12
.
a11 a21 a21
T
0
1 a11 a12 a22 a12
1 a11a22 a12 a21
AA
0
a21a12 a11a22
det A a21 a22 a21 a11 det A
1
0 1 0
1 det A
E.
det A 0 1
det A 0
Аналогично доказывается, что A 1 A E .

15.

a11 x1 ... a1n xn b1
...
...
...
- система линейных алгебраических
a x ... a x b
mn n
m
m1 1
уравнений (СЛАУ), где известные числа ai j - коэффициенты
СЛАУ, известные числа b1 ,..., bm - свободные члены, ЛЕКЦИЯ 3
неизвестные, искомые числа x1 ,..., xn - решение СЛАУ.
2014
a11 ... a1n
b1
A : ... ... ... - матрица коэффициентов, B ...
a
b
m1 ... amn
m
x1
матрица свободных членов, X ... - матрица неизвестных
x
n

16.

a11 ... a1n x1 b1
... ... ... ...
am1 ... amn xn bm
AX B - матричная запись СЛАУ.
a11 ... a1n b1
A : ... ... ... ... - расширенная матрица СЛАУ.
a
m1 ... amn bm
x1 x2 1
x1
1 1
1
1 1 1
Пр.
A
, X , B , A
x
x
2
x
1
1
2
1
1
2
1 2
2
СЛАУ совместная, если она имеет хотя бы одно решение.
В противном случае СЛАУ несовместная.
1 1 x1 1
Пр. Матричное уравнение СЛАУ имеет вид
.
1 1 x2 2
1 1
1 1 1
1, rang
2.
СЛАУ несовместная и rang
1 1
1 1 2

17.

Две СЛАУ с одинаковым числом неизвестных называются
эквивалентными, если они обе несовместные или обе совместные и имеют одинаковые множества решений.
ЗАМЕЧАНИЕ СЛАУ переходит в эквивалентную при
следующих элементарных преобразованиях:
1) перестановка местами двух уравнений,
2) умножение какого-либо уравнения на неравное нулю число,
3) поэлементное прибавление к одному уравнению другого
уравнения.
СЛАУ определенная, если она имеет ровно одно решение и
неопределенная, если решений больше одного.
Пр.

18.

ТЕОРЕМА 2.2
ЛЕКЦИЯ 3 14.09.18
1) (критерий Кронекера-Капелли совместности СЛАУ)
СЛАУ совместна тогда и только тогда, когда ранг матрицы этой
СЛАУ равен рангу расширенной матрицы.
2) (критерий определенности СЛАУ)
Для того чтобы СЛАУ была определенной необходимо и
достаточно, чтобы она была совместной и ранг матрицы
коэффициентов совпадал с числом неизвестных:
rang A rang A n .
3) (формулы Крамера) Определенная СЛАУ с помощью
элементарных преобразований приводится к СЛАУ, у которой
матрица коэффициентов A квадратная и det A 0. В этом случае
решение СЛАУ вычисляется по формулам Крамера
n
1
,
x1
, ... , xn
где : det A, i -определитель, получаемый из заменой в
нем i-ого столбца на столбец свободных членов.

19.

◄ Ограничимся доказательством того, что из
совместности СЛАУ следует равенство rang A rang A .
1) Так как все миноры матрицы A являются минорами
матрицы A , то по определению ранга rang A rang A .
2) Пусть X есть ненулевое решение СЛАУ: AX=B. Если
c1 ( A),..., cn ( A) - матрицы, образованные из столбцов матрицы A,
n
то равенство AX=B можно переписать в виде xk ck ( A) B
k 1
Любой минор матрицы A есть либо минор матрицы A, либо (в
силу теоремы 2.1.4) алгебраическая сумма миноров матрицы A.
Если он не равен нулю, то существует 0 минор матрицы
A. rang A rang A .
Следовательно, rang A rang A
СЛЕДСТВИЕ СЛАУ с m=n определенная
rang ( A) n det A 0 .

20.

Элементарные преобразования матрицы:
1) перестановка двух строк;
2) прибавление к одной строке соответствующих элементов другой
строки;
3) поэлементное умножение какой-либо строки на не равное нулю
число.
ЗАМЕЧАНИЕ СЛАУ преобразуется в эквивалентную СЛАУ,
если ее расширенную матрицу подвергнуть элементарным
преобразованиям.

21.

Метод Гаусса это метод решения СЛАУ с помощью
элементарных преобразований по следующему правилу:
0
b1'
...
0
bm'
0
1
x1 x10
b1"
0 x10
... .. 1 .. ... ...
0
0
0
bm"
1
x
x
x
n
n
n
Пр.1 ЛЕКЦИЯ 4
3x1 x2 2
3 1 2 1 2 3
1 2 3 5 I 2 II
~
~
~
1 2 3 3 1 2 II 3I 0 5 7
x1 2 x2 3
5 0 1 15
~
1
0 5 7 5
x1 0, 2
1 0 0, 2
0 1 1, 4 x 1, 4 .
2
Гаусс

22.

м
x1 - x2 + 2 x3 - x4 + 2 x5 = 1
п
п
Пример Найти общее решение СЛАУ н
.
п
п
о- 2 x1 + 2 x2 - 3 x3 + x4 - x5 = 2
ЛЕКЦИЯ 4 16.09.16
ЛЕКЦИЯ 3 15.09.17 ЛЕКЦИЯ 3 14.09.18 ЛЕКЦИЯ 3 25.09.19
ж 1 - 1 2 - 1 2 1ц
ж1 - 1 2 - 1 2 1ц
I - 2 ЧII
ч
ч
з
з
ч
ч
: з
:
з
ч
ч
чII + 2 ЧI
ч
зи- 2 2 - 3 1 - 1 2ш
зи0 0 1 - 1 3 4ш
ж1 - 1 0 1 - 4 - 7ч
ц
ж1 0ц
з
ч
ч
: з
Ю det зз
= 1 Ю x1 , x3 - базисные
ч
ч
ч
зи0 0 1 - 1 3 4 ч
з
и0 1ш
ш
переменные. x2 , x4 , x5 - свободные переменные.
м
x1 - x2 + x4 - 4 x5 = - 7
п
п
п
п
x3 - x4 + 3 x5 = 4
п
п
Ю п
Ю
нx2 = a
п
п
x4 = b
п
п
п
п
п x5 = g
о
решение СЛАУ.
мx1 = a - vb + 4g - 7
п
п
п
п
x2 = a
п
п
п
, a , b, g О R , - общее
н x3 = b- 3g + 4
п
п
x4 = b
п
п
п
п
п x5 =
о
ЛЕКЦИЯ 4 16.09.14

23.

§ 2.2 Векторное пространство и его свойства.
Векторное (линейное) пространство - множество, для
элементов которого определены операции сложения и умножения
на число, удовлетворяющие следующим аксиомам (Пеано):
1) x, y E x y y x , ЛЕКЦИЯ 3 22.09.21
2) x, y, z E ( x y ) z x ( y z ) ,
3) 0 E x E 0 x x ,
4) x E ( x) E x ( x) 0 ,
5) , R x E ( ) x ( x) ,
6) , R x E ( ) x x x ,
7) R x, y E ( x y) x y ,
8) x E 1 x x .
ЛЕКЦИЯ 4 18.09.15
Пр. Множество чисел R - векторное пространство, а множества чисел
N., Z, Q, I - нет.
Линейная комбинация элементов e1 , ..., en E - это сумма вида 1e1 ... nen ,
где 1,..., n - действительные числа, называемые коэффициентами разложения.

24.

ЛЕКЦИЯ 4 21.09.18
Элементы e1 , ..., en E линейно зависимы, если существует равная
нулю линейная комбинация этих элементов, в которой не все
коэффициенты равны нулю.
В противном случае элементы
линейно независимы.
Пр. Орты в евклидовой плоскости:
ЗАМЕЧАНИЕ Элементы линейно зависимы хотя бы один из
них представим в виде линейной комбинации остальных.
Последовательность элементов e1 ,..., en E полная (является
базисом) в векторном пространстве E, если каждый элемент из
E представим (единственным образом) в виде линейной
комбинации этих элементов.
ЗАМЕЧАНИЕ Базис является полной системой. Обратное,
вообще говоря, неверно.
Пр.

25.

ТЕОРЕМА 2.3 1) Последовательность элементов e1 ,..., en
является базисом в векторном пространстве Е она является
полной и линейно независимой системой.
2) Базисы в векторном пространстве имеют одинаковое число
элементов.
Если в векторном пространстве существует базис, то число
элементов n этого базиса - размерность пространства E, а
пространство называется n- мерным.
Обозначение dim E : n (от лат. dimension- размерность).
Векторное пространство называется бесконечномерным,
если в нём не существует базис с конечным числом элементов.
{
Пр. Пространство P : a0 x n a1 x n 1 ... an 1 x an : ak R , n N {0}
всех многочленов бесконечномерное.

26.

Последовательность элементов e1 ,..., en является базисом в векторном
пространстве Е она является полной и линейно независимой системой.
◄

27.

◄ 1) Доказательство от противного. Пусть e1 ,...en линейно
зависимы и, например, 1 0. Тогда нулевой элемент имеет два
различных разложения 0 1 e1 ... n en и 0 0 e1 ... 0 en ,
что противоречит определению базиса.
(от противного). Пусть какой-либо элемент имеет два
различных разложения: x 1e1 ... n en , x 1e1 ... n en и,
например, 1 1 . Тогда ( 1 1 )e1 ... ( n n )en 0 , что проти
воречит условию линейной независимости элементов e1 ,..., en .

28.

2) Пусть f1 ,..., f m , e1 ,...en - два базиса в Е. Пусть для
e1 11 f1 ... m1 f m
определенности m n . По условию . . . . . . . . .
e f ... f
1n 1
mn m
n
a11 x1 ... a1n xn 0
Покажем, что СЛАУ . . . . . . . . имеет единственное
a x ... a x 0
mn n
m1 1
(нулевое) решение. Пусть, от противного, есть ненулевое
решение x10 ,..., xn0 . Умножая строки предыдущей системы на
соответствующие xi0 и почленно их складывая, получим:
x10 e1 ... xn0en ( 11 x10 ... 1n xn0 ) f1 ...
( m1 x10 ... mn xn0 ) f m 0
Так как e1 ,..., en базис, то x10 ... xn0 0 . Это противоречит
предположению, и значит СЛАУ имеет единственное
решение. Это возможно только в случае m n .

29.

Декартово произведение векторных пространств E и F - это
декартово произведение соответствующих множеств
E F : {x, y}: x E , y F ,
на котором определены операции сложения элементов и
умножения их на число по правилу: {x, y}: { x, y},
{x1 , y1} {x2 , y2 }: {x1 x2 , y1 y2 }.
ЗАМЕЧАНИЕ 1 Аналогично определяются декартовы
произведения n пространств E1 ... En и E n : E ... E .
n
ЗАМЕЧАНИЕ 2 Операции над элементами декартова произве
дения удовлетворяют 8 аксиомам.
ПРИМЕР 1 Пространство векторов
V3 с общим началом.
ЗАМЕЧАНИЕ 3 вектора образуют
базис в V3 они не компланарные.

30.

ПРИМЕР 2 Пространство комплексных чисел .
i : 1 - мнимая единица. z : a b i -комплексное число, a, b R
(a1 b1i ) (a2 b2i ) : (a1 a2 ) (b1 b2 ) i
(a bi) (0 0i) (a 0) (b 0)i a bi ЛЕКЦИЯ 5
Пр.1 (c 0 i)(a bi) (ca 0 b) (cb 0 a) i ca cbi c(a bi ) c 0i c
ЗАМЕЧАНИЕ Множество комплексных чисел удовлетворяет
аксиомам 1)-8) векторного пространства относительно операций
сложения и умножения на действительное число.
Пр.2 Число a bi : a ( b)i противоположное числу z : a bi .
Последовательность 1, i образует базис в dim 2 .
z a bi - сопряженное число к комплексному числу z : a bi .
z z a 2 b2 R .
Пр.3 x 2 4 x 5 0 x1,2 2 4 5 2 i .ЛЕКЦИЯ 5 19.09.16
Проверка. 2 i 4 2 i 5 4 4i i 2 8 4i 5 0 .
2

31.

ПРИМЕР 3 Пространство M m,n матриц размера m n .
a11 ... a1n
ЗАМЕЧАНИЕ Матрица A : ... ... ... является противопо
a
m1 ... am,n
ложной к матрице A (aij ) . Попарно различные матрицы размера
m n в количестве m n штук, у каждой из которых один элемент
равен 1, а остальные равны 0, образуют базис в пространстве M m,n
1 0 0 1 0 0 0 0
Пр.
- базис в M 2,2 .
,
,
,
0 0 0 0 1 0 0 1
& A M 2,2
1 0
0 1
0 0
0 0
A a11
a12
a21
a22
0 0
0 0
1 0
0 1
a11 0 0 a12 0 0 0 0 a11
0 0 0 0 a21 0 0 a22 a21
a11 a12 a21 a22 0 .
a12 0 0
a22 0 0

32.

ПРИМЕР 4 Пространство Pn многочленов степени n .
[ p q]( x) (a0 b0 ) (a1 b1 ) x ... (an bn ) x n
( a0 b0 ) ( a1 b1 ) x ... ( an bn ) x n ЛЕКЦИЯ 4 19.09.17
( a0 ... an x n ) ( b0 ... bn x n ) p( x) q( x) .
ЗАМЕЧАНИЕ 1 Множество Pn удовлетворяет аксиомам 1)-8), и
потому является векторным пространством.
ЗАМЕЧАНИЕ 2 Последовательность многочленов x 0 : 1, x, ,..., x n
является базисом в Pn . Поэтому dim Pn n 1.
полна в P .
Пусть p( x) a 1 a x ... a x 0 0 1 0 x ... 0 x .
◄ p( x) : a01 a1 x ... an x n 1, x, ,..., x n
n
0
1
n
n
n
По определению равенства двух многочленов k n ak 0 .
1, x, ,..., x n линейно независима в Pn .
Остается воспользоваться теоремой 2.3.1.

33.

ПРИМЕР 5 Арифметическое пространство n ЛЕКЦИЯ 5
Ввели Кэли и Грассман (1946).
ЗАМЕЧАНИЕ 1 Множество n удовлетворяет аксиомам 1)-8), и
потому является векторным пространством.
ЗАМЕЧАНИЕ 2 Элементы
e1 : {1,0,...,0}, e2 : {0,1,0,...,0}, ... , en : {0,...0,1}
образуют естественный базис в n . Следовательно, dim n n .
◄ 1) a n a1e1 ... an en {a1 , a2 ,..., an } a , то есть
последовательность e1 ,..., en полна в n .
2) По определению равенства двух n-ок в n
a1e1 ... an en {a1 ,..., an } {0,...,0} a1 ... an 0 .
Следовательно, условия теоремы 2.3.1 выполнены.
ЗАМЕЧАНИЕ 3 Аналогично определяется пространство C n над
полем комплексных чисел C .

34.

§ 2.3 Линейные операторы. Евклидово пространство.
Отображение множества A в множество B - правило,
сопоставляющее каждому элементу из A один элемент из B .
В случае A B отображение называется преобразованием
пространства. ЛЕКЦИЯ 5 20.09.14
Обозначение: F : A B .
A - область определения.
B - область значений.
y F ( x) - образ элемента.
Множество значений (образ отображения)
F ( A) : y B : x A y F ( x) .
Пр. y sin x .

35.

Отображение L из векторного пространства E в векторное простран
ство F называется линейным оператором (отображением), если
, R a, b E L( a b) La Lb .
(впервые изучались Гамильтоном и Кэли, 1853-1862 г.)
(позднелатинское operator — работник).
Пр.1 Функции, имеющие производную в фиксированной точке,
образуют векторное пространство. Операция дифференцирования
d
в таком пространстве является линейным оператором.
dx
d
d
d
(2 x 2 3sin x) 2 x 2 3 sin x .
dx
dx
dx
Пр. 2 Каждая матрица A (aij ) размера m n определяет линейный
оператор L :
n
m
по следующему правилу: если a {x1 , ..., xn } ,
y1 a11 ... a1n x1
... .
то La : { y1 , ..., yn }, где ... : ....................
y a
m m1 .... am xn
Такой оператор называется матричным.

36.

L : E F - изоморфизм векторных пространств E и F, если:
1) L переводит разные элементы в разные:
ЛЕКЦИЯ 6 21.09.15
x1 , x2 E ( x1 x2 ) ( Lx1 Lx2 ) ,
2) каждый элемент из F является образом некоторого элемента из E:
y F x E Lx y .
При этом пространства E, F называются изоморфными.
Пр. Пространства
n
и M n1 изоморфны.

37.

(в ) называется линейной
Линейный оператор из E в
формой (линейным функционалом).
b
Пр. Определённый интеграл f ( x)dx на векторном пространстве
a
интегрируемых на [a, b] функций является линейным
функционалом. Лекция 4 2.10.19
Отображение F ( x1 ,..., xn ) : F ({x1 ,..., xn }) из декартова
произведения векторных пространств E n E ... E
в векторное пространство F называется n-линейным
(полилинейным) отображением, если оно является линейным
отображением из E в F по каждой переменной xk , k 1,.., n , при
фиксированных остальных. n- линейное отображение из E n в
называется n- линейной (полилинейной) формой.
ЗАМЕЧАНИЕ 2-линейное отображение F ( x1 , x2 ) : E 2 F
принято называть билинейным отображением.

38.

Билинейная форма B( x, y) : E 2 называется скалярным
произведением на векторном пространстве E, если она обладает
свойствами:
1) x, y E B( y, x) B( x, y ) ,
2) x E если ( y E B ( x, y ) 0), то ( x 0) ,
3) x 0 B( x, x) 0 .
Обозначение x, y ( x, y ) : B( x, y ) .
Пр.1 Определенное в школе скалярное произведение векторов
порождает билинейную форму B( x , y ) : V 32 по правилу
B( x , y ) : x y cos x y , и для нее выполняются свойства 1)-3).
Пр.2 Пусть x : x1 ,..., xn , y : y1 ,..., yn n . Тогда отображение
B( x, y) x, y : x1 y1 ... xn yn : n
является билинейной формой со свойствами 1) - 3). Мы будем
называть его естественным скалярным произведением в n .

39.

Отображение : E
свойствами:
1) x 0 x 0 ,
2) x E R x x ,
3) x, y E x y x y .
называется нормой, если обладает
ЗАМЕЧАНИЕ 1 Понятие нормы обобщает понятие длины
(модуля) вектора в V3 . Гаусс ввел (1831) понятие и термин норма
комплексного числа как z z . Гамильтон ввел независимо (1843)
понятие и термин норма кватерниона термин норма вектора.
Обозначение - Шмидт (1908). ЛЕКЦИЯ 4 ВИС 15.10.18
ЗАМЕЧАНИЕ 2 Каждое скалярное произведение x, y : E 2
порождает норму в E по правилу x :
x, x .
ЛЕКЦИЯ 6
СЛЕДСТВИЕ Естественное скалярное произведение в R n
2
обладает свойством : x, y R n x1 y1 ... xn yn x12 ... xn2 y12 ... yn2
(неравенство Коши-Буняковского). ЛЕКЦИЯ 5 26.09.18

40.

1) x 0 x 0 ,
2) x E R x x ,
3) x, y E x y x y .
x :
x, x .
x : x12 ... xn2 в
n
.
ЛЕММА (неравенство Коши-Буняковского
2
x, y R n x1 y1 ... xn yn x12 ... xn2 y12 ... yn2 .
◄
x y ( x1 y1 ) 2 ... ( xn yn ) 2
?
x12 ... xn2 y12 ... yn2 x y

41.

n-мерное евклидово (точечное) пространство - тройка объектов
En ( E , . , . , P) : n-мерное векторное пространство E, какое-либо
скалярное произведение x, y на нём и множество “точек” P.
Объекты согласованы следующим образом:
1) каждой упорядоченной паре точек A, B P поставлен в
соответствие один элемент x E , который обозначают x AB ;
2) x E A P существует единственная точка B со свойством
x AB ;
3) A, B, C P AB BC AC (правило треугольника).
ЗАМЕЧАНИЕ Пеано - основатель концепции, по которой основными
ми элементами евклидова пространства являются вектор и точка.
Расстояние между двумя точками M1 , M 2 P
определяется по формуле ЛЕКЦИЯ 6 23.09.16
M 1 , M 2 :
M 1 M 2 , M 1M 2 M 1M 2 .
n-мерное евклидово векторное пространство - пара E , , .
n-мерное аффинное пространство - пара (E,P) со свойствами 1) -3)

42.

Пр. n- мерное арифметическое евклидово пространство n тройка объектов: арифметическое пространство n , естественное
скалярное произведение x, y : x1 y1 ... xn yn и множество
«точек» P : ( x1,..., xn ) : x1,..., xn . При этом точки A ( x1 ,..., xn ) ,
B ( y1 ,..., yn ) P свяжем с вектором из n по правилу
AB : { y1 x1 ,..., yn xn }.
Тогда расстояние между этими точками вычисляется по формуле
( A, B) :
AB, AB ( y1 x1 )2 ... ( yn xn ) 2 .
2
3
ЛЕКЦИЯ 6

43.

Декартова система координат (ДСК) в n-мерном
евклидовом пространстве E - это совокупность каких-либо
точки O P и базиса e1 ,..., en E .
Символ Кронекера – отображение i j : 2 {0,1},
определяемое по правилу i j : 1, если i j и i j : 0 , если i j .
Базис e1 ,..., en E называется ортонормированным, если
i, j n ei , e j ij .
ЗАМЕЧАНИЕ Элементы ei ортонормированного базиса попарно
перпендикулярны: i j ei , e j 0 и их нормы равны единице:
i n ei
ei , ei 1.
Прямоугольная декартова система координат (ПДСК) ДСК, в которой выделенный базис является ортонормированным.
Если a x1e1 ... xn en , то числа x1 ,..., xn называются координатами (компонентами) элемента (вектора) a в базисе e1 ,..., en .

44.

Радиусом-вектором точки М и ПДСК называется вектор OM .
Если OM x1e1 ... xn en , то n- ка ( x1 ,..., xn ) называются
координатами точки M P в ПДСК.
Пусть даны матрица A (aij ) размера (n k ) n , rang A n k ,
и последовательность чисел b1 ,..., bn k . k-мерная плоскость
(k-плоскость) в n-мерном евклидовом пространстве E с фиксированной ПДСК - это множество точек Ì ( x1 ,..., xn ) , координаты
a11 x1 . . . a1n xn b1
. . .
которых удовлетворяют СЛАУ
.
a x ... a
n k n xn bn k
n k 1 1
1-плоскость в E называется прямой. ЛЕКЦИЯ 5 26.09.17
Пр.1 2-плоскость (плоскость) в V3 - это множество точек,
координаты которых ( x1 , x2 , x3 ) удовлетворяют СЛАУ
a11 x1 a12 x2 a13 x3 b1 или проще Ax By Cz D 0 .

45.

Пр.2 Прямая в V3 - это множество точек, координаты которых
a11 x1 a12 x2 a13 x3 b1
,
( x1 , x2 , x3 ) удовлетворяют СЛАУ
a21 x1 a22 x2 a23 x3 b2
a11 a12
где rang
a21 a22
a13
2 . Или проще
a23
A1 x B1 y C1 z D1 0
.
A2 x B2 y C2 z D2 0

46.

Полярная система координат в V2 - совокупность точки O
(- полюс) и луча с началом в этой точке (- полярная ось).
Полярные координаты точки M - пара чисел (r , ) , где угол между полярной осью и вектором OM , отсчитываемый
против часовой стрелки, r OM . ЛЕКЦИЯ 6 27.09.2014
Совместим прямоугольную
декартову и полярную систеM y
M
мы координат так, чтобы наr
чало координат совпадало с
X
полюсом, а ось OX - с полярx
O
O
ной осью, как на рисунке.
Декартовы координаты (x,y) точки M и ее полярные координаты
r x 2 y 2
x r cos
связаны равенствами:
.
,
y
y r sin arctg
x
Пр. r=1 есть уравнение единичной окружности в полярной
системе координат.
Y

47.

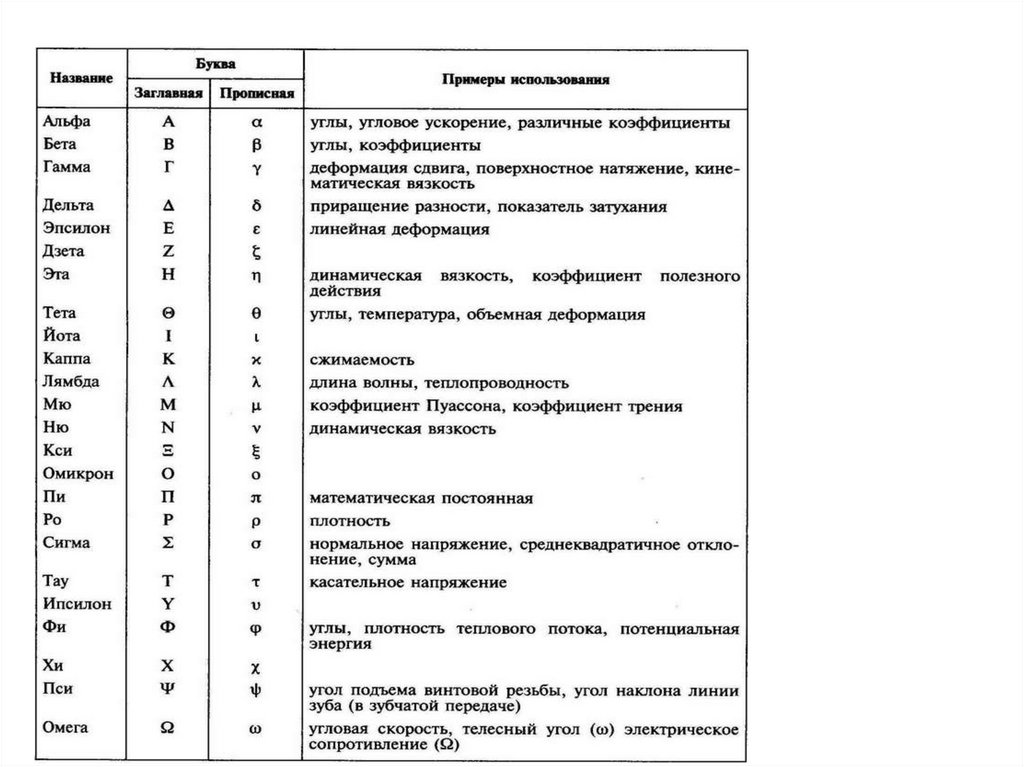
В V3 с ПДСК фиксируем точку M ( x, y, z ) .Тройка чисел ( , , ) ,
где 0 , 0 2 , 0, называется
сферическими координатами точки M.
ЗАМЕЧАНИЕ 1 Так как OM ў= zM = r sin j ,
то декартовы и сферические координаты
точки M связаны равенствами
x sin cos
y sin sin .
z cos
ЗАМЕЧАНИЕ 2 Каждая точка в V%
3 вполне определяется своими
сферическими координатами.
Пр r = 1 есть уравнение сферы в V%
3 в сферических координатах.

48.

В V3 с ПДСК фиксируем точку M ( x, y, z ) .
Тройка чисел (r , , z ) , где z R , 0 2 , r 0 ,
называется цилиндрическими
координатами точки M . ЛЕКЦИЯ 5 7.10.19
ЗАМЕЧАНИЕ 1 В ПДСК декартовы и
цилиндрические координаты точки M
x r cos
связаны равенствами y r sin .
z z
ЗАМЕЧАНИЕ 2 Из рисунка видно, что каждая точка M вполне
определяется своими цилиндрическими координатами.
Пр. r=1 есть уравнение цилиндра радиуса 1 и осью OZ в
цилиндрической системе координат.

49.

§ 2.3 Векторная алгебра в пространстве V3
Даны ось l (-направленная прямая) и
вектор. Опустим перпендикуляры из
его концов на ось. ЛЕКЦИЯ 7 28.9.15
b
a
c
l
Проекция вектора a на ось l - это расстояние между
основаниями этих перпендикуляров, взятое со знаком "+", если
0 l a
, со знаком "-", если
l a и равное нулю, если
2
2
a l . Правило, сопоставляющее каждому вектору его проекцию
на ось, называется операцией проектирования.
Пр. Если a l , то прl a 0 .
Если вектор a и ось l параллельны и сонаправлены, то прl a a .
Если вектор a и ось l параллельны и разнонаправлены, то
прl a a .

50.

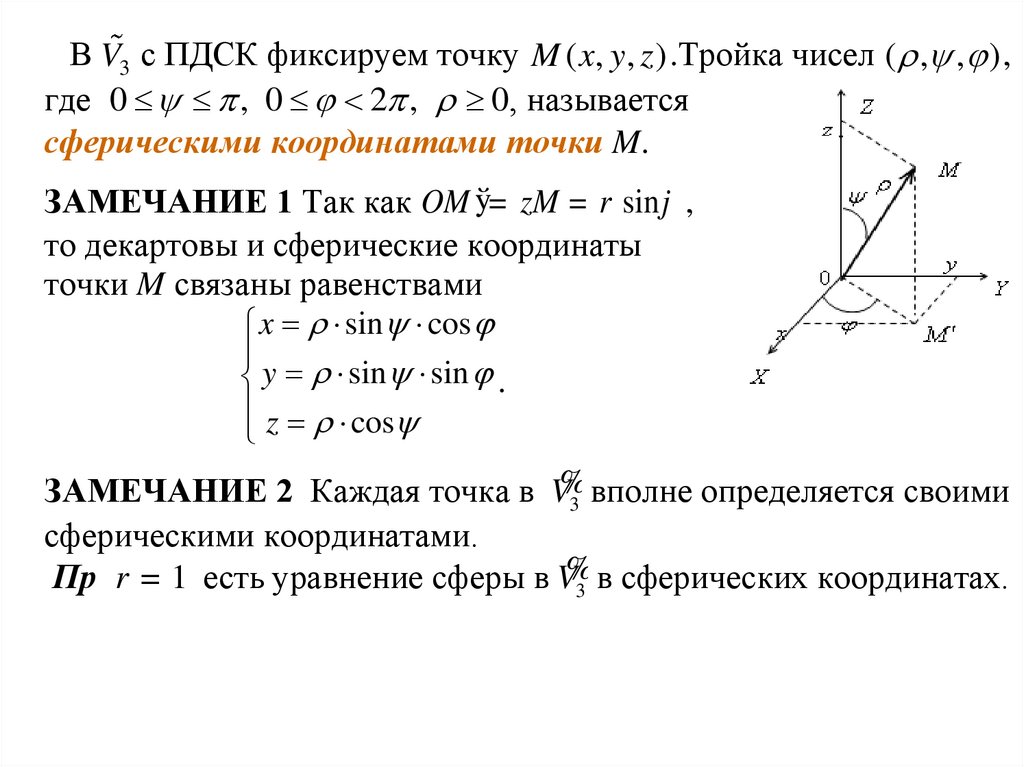
Проекция (лат. projectio - выбрасывание вперёд). Термин проекция употребляется и в отношении самой
операции проектирования, и в отношении её результата.
Центр проекции + Предмет + Картинная (проекционная) плоскость.
Аксонометрическая проекция (от др.-греч. ἄξων «ось»+μετρέω «измеряю»)
Центральная проекция
ЛЕКЦИЯ 5 УЛ11, УТС11 28.09.21
Стереографическая проекция

51.

ТЕОРЕМА 2.4 (свойства проекции)
ВИС ЛЕКЦИЯ 5 29.10.18 ЛЕКЦИЯ 7
1) прl a a cos(l a ) .
2) a , b V3 прl (a b ) прl a прl b .
3) a V3 l прl ( a ) прl a . То есть операция
проектирования является линейным функционалом в V3 .
4) Фиксируем ПДСК в V3 . Тогда проекции вектора на оси
координат OX,OY,OZ совпадают с компонентами этого вектора
в базисе i , j , k
: если a {x, y, z}, то
x прi a , y пр j a , z прk a .
5) Косинусы cos( i a ), cos( j a ), cos(k a ) называются
направляющими косинусами вектора a и связаны
равенством cos2 ( i a ) cos 2 ( j a ) cos 2 (k a ) 1.

52.

◄
4) Подействуем на равенство a xi yj zk линейной опера-
цией проектирования на ось OX: прi a x прi i y прi j z прi k x ,
прk a x прk i y прk j z прk k z .
5) По свойству гипотенузы прямоугольного
параллелепипеда и пунктам 1), 4)
2
a x 2 y 2 z 2 a 2 cos2 i a a 2 cos2 j a a 2 cos2 k a
1 cos 2 cos 2 cos 2 , ЛЕКЦИЯ 7 30.09.16
где : i a , : j a , : k a .

53.

ЗАМЕЧАНИЕ Если точка C ( x, y, z ) делит отрезок AB
A
B
C
с концами в
CB
точках A( x1 , y1 , z1 ), B( x2 , y2 , z2 ) в отношении
,
AC
0
то ее координаты вычисляются по формулам
x x2
y yx2
z z2
.
x 1
, y 1
, z 1
◄ Построим радиусы-векторы OA, OB, OC и векторы AC , AB .
AC AB
AC
1
Имеем
AC
AB
AB
AB
AC AB
AC CB
1 /
AB {x2 x1 , y2 y1 , z2 z1} OC OA AC x1
( x2 x1 ), y1
( y2 y1 ),
x1 x2 y1 y2 z1 z2
z1
( z2 z1 )
,
,
.

54.

Скалярное произведение векторов a , b это число
a b (a, b) a b cos ab .
ЛЕКЦИЯ 7
ЛЕКЦИЯ 6 28.09.18
ТЕОРЕМА 2.5 (свойства скалярного произведения)
1) a a = a 2 , где a = a . 2) ab = 0 Ы (a = 0) Ъ (b = 0) Ъ (a ^ b) .
3) a b = b a . 4) a b = a Чпр a b = b Чпр b a .
5) Скалярное произведение является билинейной формой на V32 .
6) Если a x1 , y1 , z1 , b x2 , y2 , z2 , то a b x1 x2 y1 y2 z1 z2 .
Физическое приложение
Работой постоянной силы F по
перемещению материальной точки из
начала в конец вектора s называется
величина A : F s .
S
F
F
F
F
F
F
A : F s

55.

Упорядоченная тройка некомпланарных векторов
a, b, c с общим началом называется правой (левой),
если из конца вектора c движение от a к b по
кратчайшему из двух углов происходит против
(по) часовой стрелки.
ЗАМЕЧАНИЕ Обычно предполагается, что орты i , j , k в ПДСК
образуют правую тройку.
Векторное произведение векторов a , b это вектор 0 , если
(a 0) (b 0) (a || b) . В противном случае
[a,b]
c
векторное произведение это вектор c , который
вполне определяется свойствами:
a
b
1) | c | a b sin ab ,
2) c a , b ,
3) a , b, c - правая тройка векторов.
Пр. [ i , j ] k , [ j, k ] i, [k , i] j, [ j , i ] k , [k , j ] i, [i, k ] j .

56.

Смешанное произведение трёх векторов a , b, c - это число
abc : ([a , b ], c) .
ЗАМЕЧАНИЕ 1 ЛЕКЦИЯ 6 29.09.17
1) (геометрический смысл модуля векторного произведения)
| [a , b] | численно равен площади параллелограмма, построенного
на векторах a , b как на сторонах.
2) (геометрический смысл модуля смешанного произведения)
| a b c | численно равен объему призмы, построенной на векторах
a , b, c как на ребрах. ВИС ЛЕКЦИЯ 6 12.10.18
·
| a b c |= | [a , b ] | Ч| c | Ч| cos([a , b] c) |= | [ a , b ] | Чпр[ a ,b ]c = Sпар Чh = Vприз .
ЗАМЕЧАНИЕ 2 Тройка a , b, c правая векторы [a , b ], c находят
ся в одном полупространстве, определяемом плоскостью векторов
·
a , b [a , b ] c / 2 a b c = | [a , b ] | Ч| c | Чcos([a , b] c) > 0
смешанное произведение a b c положительное.
ЗАМЕЧАНИЕ 3 a bc bc a c a b b a c a c b c b a .

57.

ТЕОРЕМА 2.6 (свойства векторного произведения)
1) a , b b , a .
2) Векторное произведение является билинейным отображением из
V32 в V3 .
i
3) Если a x1 , y1 , z1 , b x2 , y2 , z2 , то a , b x1
x2
j
y1
y2
k
z1 .
z2
СЛЕДСТВИЕ Ненулевые векторы a = {x1 , y1 , z1}, b = {x2 , y2 , z2 }
x1
y1
z1
параллельны Ы
. ЛЕКЦИЯ 7 30.09.14 ЛЕКЦИЯ 8 2.10.15
=
=
x2
y2
z2
Физический смысл векторного произведения:
Моментом относительно точки A силы FB ,
приложенной к точке B, называется вектор A
M A [ FB ] : [ AB, FB ] .
F
M A [ FB ]
B

58.

Физический смысл векторного произведения:
Пусть материальная точка A вращается по
окружности (с центром O) с линейной
O
скоростью v A . Вектор угловой скорости
r
вращения точки A относительно цента O
это расположенный на оси вращения вектор
, определяемый равенством vA [ , r ] .
Равенство называется формулой Эйлера. ЛЕКЦИЯ 6 9.10.19
vA
A
ТЕОРЕМА 2.7 (свойства смешанного произведения)
1) abc 0 (a 0) (b 0) (c 0) (векторы a , b , c
компланарны).
2) Смешанное произведение является 3– линейной формой:
a b c : V33 .
3) Если a {x1 , y1 , z1}, b {x2 , y2 , z2 }, c {x3 , y3 , z3} в ПДСК, то
x1
a b c x2
x3
y1
y2
y3
z1
z2 .
z3

59.

§ 2.4 Прямые и плоскости ЛЕКЦИЯ 8 3.10.16
в евклидовых пространствах V2 , V3 ЛЕКЦИЯ 8
L : Ax + By + Cz + D = 0 - общее уравнение плоскости в V3
:= {( x, y, z ) : Ax + By + Cz + D = 0}.
(A,B,C 0 одновременно). L=
ЗАМЕЧАНИЕ Уравнение впервые встречается у Клеро (1731).
Вектор нормали к плоскости - вектор, перпендикулярный любому
вектору, начало и конец которого лежат в этой плоскости.
Пр.1 Вектор n := { A, B, C} является вектором нормали к
плоскости L : Ax + By + Cz + D = 0.
Пр.2 Орт i является вектором нормали к координатной плоскости
YOZ : x 0 .
Угол между плоскостями - угол между их векторами нормалей.
В зависимости от выбранных векторов нормалей этот угол имеет
два значения.
ВИ 13.10.21

60.

ТЕОРЕМА 2.8 (свойства плоскости в V3 ) Пусть заданы 3 плоскос
A1 B1 C1
A1 B1 C1 D1
ти L ii : Ai x Bi y Ci z Di 0, i 1,2,3, A : A2 B2 C2 , A : A2 B2 C2 D2
A B C
A B C D
3
3
3
3 3
3 3
A1 B1 C1
A1 B1 C1
rang
1.
1) L 1 || L 2
A2 B2 C2
A2 B2 C2
A1 B1 C1 D1
A1 B1 C1 D1
rang
1.
2) L 1 L 2
A2 B2 C2 D2
A2 B2 C2 D2
3) Плоскости L 1 , L 2 , L 3 пересекаются по одной прямой тогда и
только тогда, когда rangA rangA 2.
4) Плоскости L 1 , L 2 , L 3 пересекаются в одной точке т огда и только
тогда, когда rang A 3 det A 0 . ВИС ЛЕКЦИЯ 7 26.10.18
5) cos L 1L 2
A1 A2 B1B2 C1C2
A B C A B C
2
1
2
1
2
1
2
2
2
2
2
2
. ЛЕКЦИЯ 7 3.10.17
6) Расстояние от точки M 0 x0 , y0 , z0 до плоскости L 1 вычисляется
по формуле M 0 , L 1
A1 x0 B1 y0 C1 z0 D1
A B C
2
1
2
1
2
1
. ЛЕКЦИЯ 8 4.10.14

61.

Пр.1 Составить уравнение плоскости, проходящей через три
точки M i ( xi , yi , zi ), i 1,2,3, не лежащие на одной прямой.
M3
M1
M
M2
УА 30.09.21
Пр.2 Найти общий вид уравнения плоскости, проходящей через
заданную точку M 0 ( x0 , y0 , z0 ) .

62.

Пусть векторы a : { 1, 1, 1}, b : { 2 , 2 , 2} не коллинеарны, и
задана точка M 0 ( x0 , y0 , z0 ) . Система уравнений УТС 30.09.21
x 1u 2v x0
измерять одну вещь
y
u
v
y
,
u
,
v
R
,
1
2
0
с
помощью
другой
.
Термин
Лейбница
,1684
z u v z
1
2
0
определяющая множество точек с координатами ( x, y, z ) в V3 ,
называется параметрическим уравнением плоскости.
Запишем систему в векторной форме M 0 M ua vb , M x, y, z =
произвольная точка плоскости. Так как векторы M 0 M , a , b
компланарны, по критерию компланарности равно нулю их
смешанное произведение
1 1
1 1
1 1
M 0M , a , b
( x x0 )
( y y0 )
( z z0 ) 0 ,
2 2
2 2
2 2
а это уравнение плоскости.

63.

ЗАМЕЧАНИЕ Если плоскость задана уравнением
A( x x0 ) B( y y0 ) C ( z z0 ) 0
и для определенности A 0 , то ее параметрическое уравнение
B
C
x
u
v x0
A
A
можно задать, в виде: y u y0
, u, v R .
z v z0

64.

ЗАМЕЧАНИЕ 1Пусть в какой-либо ПДСК евклидовой плоскости V2 заданы две прямые l1 , l2 уравнениями Ai x Bi y Ci 0, i 1,2
Тогда справедливы утверждения.
1) l1 || l2
2) l1 l2
A1 B1
.
A2 B2
A1 B1 C1
.
A2 B2 C2
3) cos l1 l2
A1 A2 B1B2
A B A B
2
1
2
1
2
2
2
2
.
4) Расстояние от точки M 0 ( x0 , y0 ) до прямой l1 вычисляется по
формуле ( M 0 , l1 )
A1 x0 B1 y0 C1
A B
2
1
2
1
.
ЗАМЕЧАНИЕ 2 В современной форме основные задачи на
прямую впервые изложил Лакруа (1799).

65.

Множество точек, координаты которых ( x, y, z ) удовлетворяют
A1 x B1 y C1 z D1 0
A1
СЛАУ l :
, где rang
A2 x B2 y C2 z D2 0
A2
B1
B2
C1
2,
C2
называется общим уравнением прямой в V3 .
A1 x B1 y C1 z D1 0
l : ( x, y, z ) V3 :
.
A2 x B2 y C2 z D2 0
Множество точек, координаты которых ( x, y, z ) удовлетворяют
СЛАУ
A1 ( x x0 ) B1 ( y y0 ) C1 ( z z0 ) 0
A2 ( x x0 ) B2 ( y y0 ) C2 ( z z0 ) 0
A1
где rang
A2
B1
B2
(1),
C1
2 , называется общим уравнением прямой в
C2
V3 , проходящей через точку M 0 ( x0 , y0 , z0 ) .

66.

Пусть дан вектор k {m, n, p} 0 и точка M 0 ( x0 , y0 , z0 ) .
x x0 y y0 z z0
2
m
n
p
называется каноническим уравнением прямой (Коши, 1826).
Вектор k - направляющий вектор прямой l (Лагир, 1685) .
Формула, определяющая множество точек в V3 с координатами
Система уравнений вида
x mt x0
y nt y0 , t R
z pt z
0
(3) ,
называется параметрическим уравнением прямой (Коши,
1826). ЛЕКЦИЯ 9 7.10.16
ЗАМЕЧАНИЕ 1 Направляющий вектор k параллелен любому
вектору, начало и конец которого лежат на этой прямой.

67.

ЗАМЕЧАНИЕ 2 Уравнения (1), (2), (3), в которых
B1 C1
C1
m :
, n :
B2 C2
C2
A1
A1 B1
,
, p :
A2
A2 B2
задают одну и ту же прямую в V3 .
ЛЕКЦИЯ 7 16.10.19
____
Угол между двумя прямыми - угол между направляющими
векторами этих прямых. Этот угол принимает два значения.

68.

ТЕОРЕМА 2.9 (свойства прямых) Пусть даны две прямые
x2 x1 y2 y1
x xi y yi z zi
n1
li :
, i 1, 2 и A : m1
mi
ni
pi
m
n2
2
m1 n1 p1
m1 n1 p1
1) l1 l2
rang
1;
m
n
p
m2 n2 p2
2
2
2
z2 z1
p1 . Тогда :
p2
ЛЕКЦИЯ 9.13
m
n
p x x
y y z z
1 1 1 2 1 2 1 2 1 rang A 1;
n1
p1
m2 n2 p2 m1
m1 n1 p1
3) l1 , l2 пересекаются rangA rang
2;
m
n
p
2
2
2
2) l1 l2
4) l1 , l2 скрещиваются det A 0 rang A 3 ;
5) cos l1 l2
m1m2 n1n2 p1 p2
p12 n12 p12
m22 n22 p22
;
6) Расстояние от точки
M 0 ( x0 , y0 , z0 ) до прямой l1 вычисляется по формуле ( M 0 , l1 )
[ M 0 M 1 , k1 ]
| k1 |
;
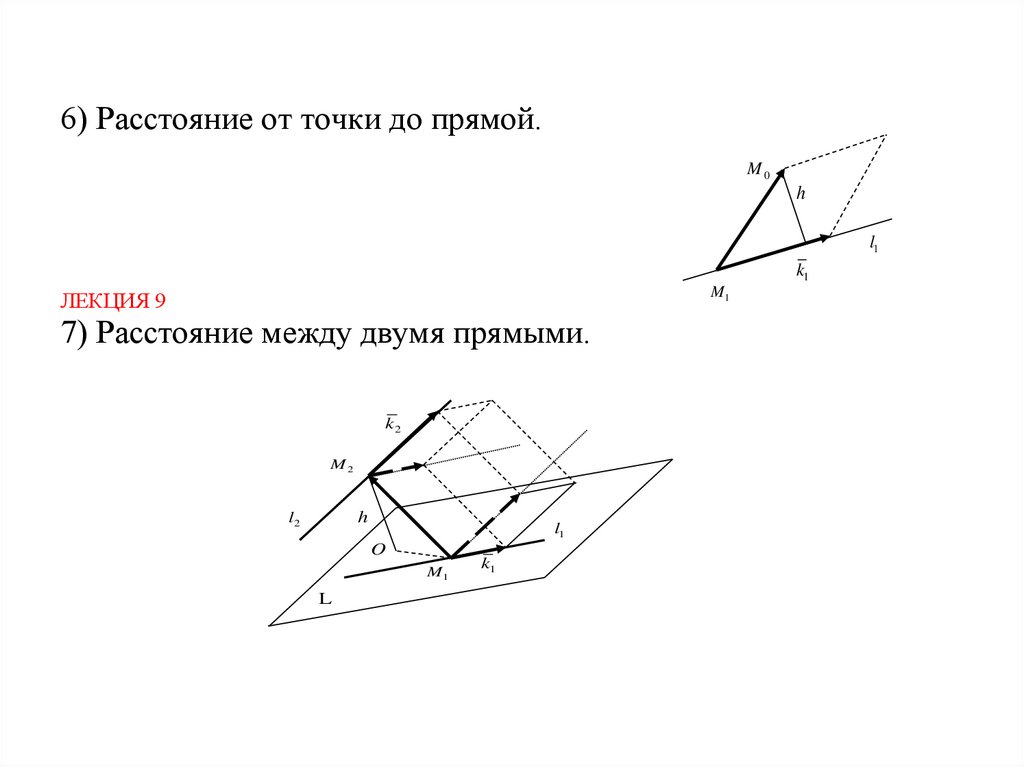
7) Расстояние между двумя прямыми l1 , l2 вычисляется по формуле
(l1 , l2 )
(k1 , k2 , M 1M 2 )
| [k1 , k2 ] |
. ЛЕКЦИЯ 9 05.10.15

69.

6) Расстояние от точки до прямой.
M0
h
l1
k1
M1
ЛЕКЦИЯ 9
7) Расстояние между двумя прямыми.
k2
M2
h
l2
l1
O
M1
L
k1

70.

ЗАМЕЧАНИЕ 1) Ax By C 0 - общее уравнение прямой.
x x1 y y1
2)
, k : {m, n}, - каноническое уравнение прямой.
m
n
x x1
y y1
3)
- уравнение прямой, проходящей через две
x2 x1 y2 y1
точки M1 ( x1, y1 ), M 2 ( x2 , y2 ) .
x mt x0
, t R - параметрическое уравнение прямой.
y nt y0
4)
5)
x y
1 - уравнение прямой "в отрезках на осях".
a b
6) cos x sin y p 0 - нормальное уравнение прямой, где
n {cos , sin } - единичный вектор нормали к прямой, а
p cos x sin y (n , OM ) прn OM есть проекция радиусоввекторов точек M прямой на направление вектора нормали.

71.

§ 2.4 Алгебраические кривые второго порядка
в евклидовой плоскости V2 ЛЕКЦИЯ 9 11.10.14
Кривая второго порядка в V2 - множество точек, координаты
которых в какой-либо ПДСК удовлетворяют уравнению
a11 x 2 2a12 xy a22 y 2 b1x b2 y c 0
где a11, a12 , a22 0 одновременно. ЛЕКЦИЯ 8 10.10.17 ЛЕКЦИЯ УА11 5.10.21
Пр. Окружность в ПДСК в V2 задается уравнением
( x x0 )2 ( y y0 )2 R 2 ,
и имеет параметрическое уравнение x R cos t x0 , t [0,2 ].
y R sin t y
0
Кпр. Уравнение x2 y 2 1 0 задает пустое множество точек в V2 .
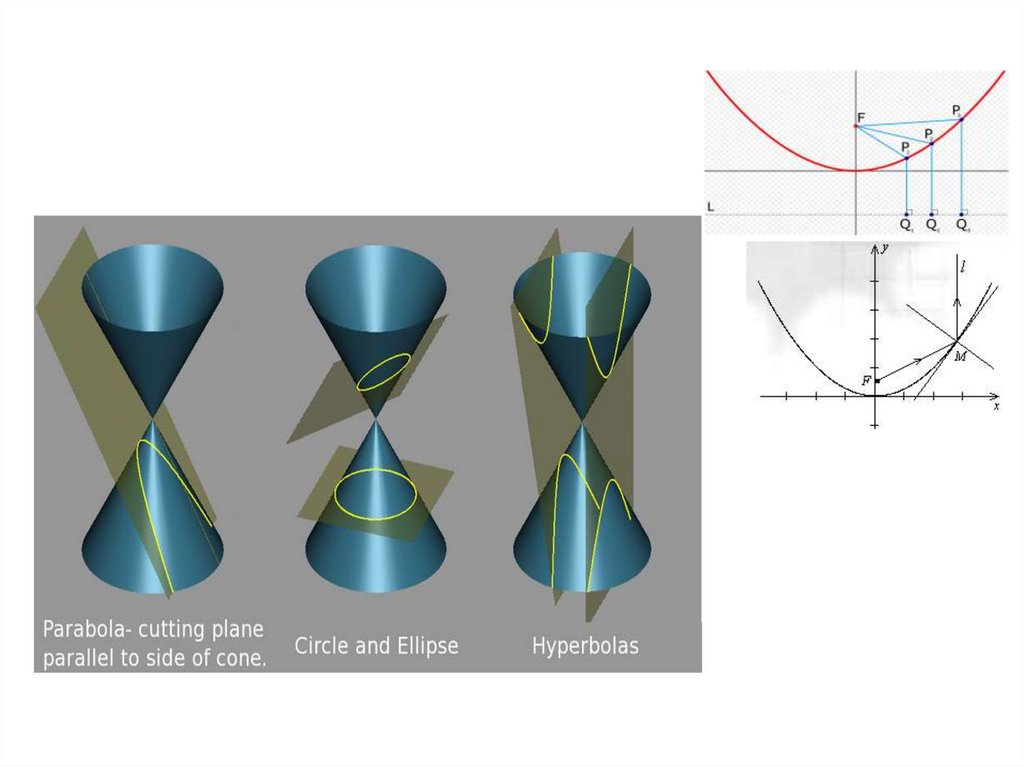
ЗАМЕЧАНИЕ Невырожденных кривых второго порядка 3 типа.
Невырожденных кривых третьего порядка – десятки типов
(классификация Ньютона).
Литература: Савёлов А.А. Плоские кривые.

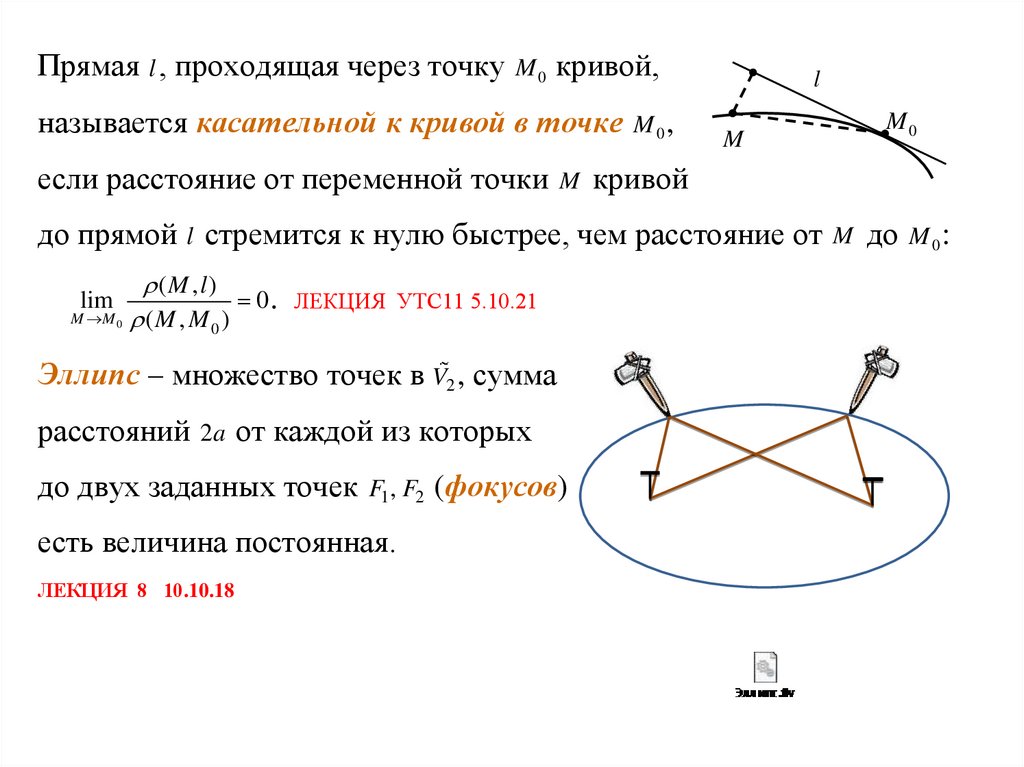
72.

Прямая l , проходящая через точку M 0 кривой,
называется касательной к кривой в точке M 0 ,
l
M
M0
если расстояние от переменной точки M кривой
до прямой l стремится к нулю быстрее, чем расстояние от M до M 0 :
(M , l )
0 . ЛЕКЦИЯ УТС11 5.10.21
M M 0 ( M , M )
0
lim
Эллипс – множество точек в V2 , сумма
расстояний 2a от каждой из которых
до двух заданных точек F1, F2 (фокусов)
есть величина постоянная.
ЛЕКЦИЯ 8 10.10.18

73.

ТЕОРЕМА 2.10
1) Пусть F1 ( c,0), F2 (c,0) , b := a 2 - c 2 , b < a .
x2 y 2
Тогда каноническое уравнение эллипса имеет вид 2 + 2 = 1.
a
b
c
b2
2) Эксцентриситет эллипса e := = 1- 2 О (0,1) . Если
a
a
a const и 1, то эллипс сжимается к отрезку [ a, a ] оси OX;
Если 0 , то эллипс выпрямляется в окружность x2 y 2 a 2 .
3) Уравнение касательной к эллипсу в точке M ( x0 , y0 ) имеет вид
x0
y0
x 2 y 1.
2
a
b
[ a,0], [0, a] OX - большие полуоси.
[ b,0], [0, b] OY - малые полуоси.

74.

c
b2
Пр. (геометрический смысл эксцентриситета) e := = 1- 2
a
a
Если 0 , то уравнение эллипса
x2 y 2
2 1.
2
a
a
3
x2
y2
Если , то уравнение эллипса 2
1.
2
2
a (a 2)
Если 1, то «уравнение эллипса»
ЛЕКЦИЯ ВИС 10.12.18
x2 y 2
2 1.
2
a
0

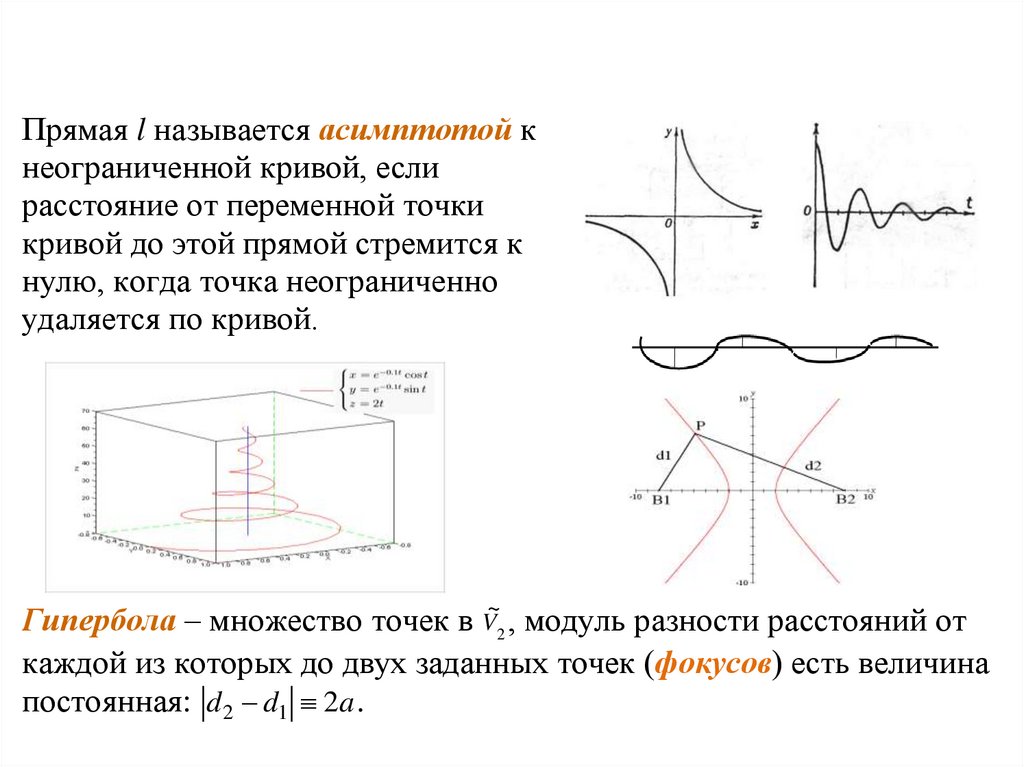
75.

Прямая l называется асимптотой к
неограниченной кривой, если
расстояние от переменной точки
кривой до этой прямой стремится к
нулю, когда точка неограниченно
удаляется по кривой.
Гипербола – множество точек в V~2 , модуль разности расстояний от
каждой из которых до двух заданных точек (фокусов) есть величина
постоянная: d 2 d1 2a .

76.

ТЕОРЕМА 2.11 1) Пусть F1 ( c,0), F2 (c,0) , b := c 2 - a 2 , b < a . Тогда
x2 y 2
каноническое уравнение гиперболы имеет вид 2 - 2 = 1.
a
b
b
a
2) y x - уравнения асимптот ветвей гиперболы. ЛЕКЦИЯ 10.13
c
b2
3) Эксцентриситет гиперболы e := = 1 + 2 О (1, Ґ ) . Если a const
a
a
и 1, то ветви гиперболы сжимаются к отрезкам ( , a], [a, ) .
Если , то ветви гиперболы разгибаются в прямые x a .
4) Уравнение касательной к гиперболе в точке M ( x0 , y0 ) имеет вид
x0
y0
x
y 1.ЛЕКЦИЯ 10 12.10.15
2
2
a
b
[ a,0], [a,0] OX -
вещественные полуоси.
[0, b], [0, b] OY -
мнимые полуоси.

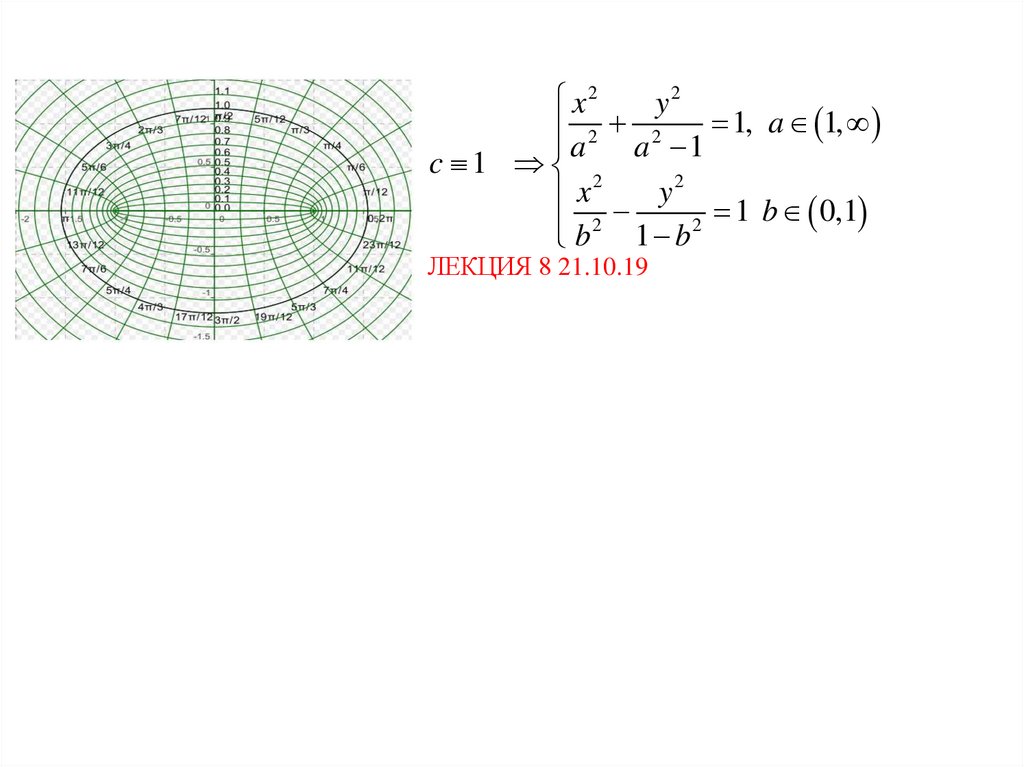
77.

x2
y2
a 2 a 2 1 1, a 1,
c 1 2
2
x y 1 b 0,1
b 2 1 b 2
ЛЕКЦИЯ 8 21.10.19

78.

Парабола - множество точек в V2 , расстояния
от которых до заданной точки F (фокуса) и до
заданной прямой l (директрисы) совпадают.
p
p
ТЕОРЕМА 2.12 1) Пусть F ,0 , l : x .
2
2
Y
l
M ( x, y )
X
p 2
0
F p 2 ,0
Тогда каноническое уравнение параболы
имеет вид y2 2 px .
ЛЕКЦИЯ 10 14.10.14
2) Точка параболы 0,0 является ближайшей к директрисе и
называется вершиной параболы.
3) y0 y p( x x0 ) - уравнение касательной к параболе y2 2 px в
точке ( x0 , y0 ) . ЛЕКЦИЯ 11 17.10.16
(M , l )
3)
M M 0 ( M , M )
0
lim
1
lim
| y0 y p ( x x0 ) |
y02 p 2 M M 0 ( x x0 ) 2 ( y y0 ) 2

79.

80.

ТЕОРЕМА 2.13 (классификация геометрических объектов,
задаваемых общим уравнением кривой второго порядка)
2
2
Уравнение кривой второго порядка a11 x 2a12 xy a22 y b1x b2 y c 0
с помощью последовательно: а) преобразования поворота ПДСК
вокруг начала координат, б) сдвига ПДСК на некоторый вектор и,
возможно, в) отражения относительно какой-то из осей координат,
может быть приведено к одному из простейших видов:
1) каноническому уравнению эллипса, гиперболы, параболы;
2) уравнению пары прямых
Y
M
x 2 y 2 0, x 2 a 2 ;
y
Y1
3) уравнению, которому
удовлетворяют координаты
j
одной точки x 2 y 2 0 ;
j1
X1
i
4) уравнению, которому не
1
удовлетворяют координаты ни
x
i
одной точки x 2 y 2 1. УА 7.10.21
O
X

81.

ЗАМЕЧАНИЕ Исключение слагаемого 2a12 xy из уравнения
a11 x 2 2a12 xy a22 y 2 b1x b2 y c 0
поворотом ПДСК на угол j .
2a12
1
j = arctg
Ю
2
a11 - a22
м
x = cos j x1 - sin j y1
п
п
н
п
п
о y = sin j x1 + cos j y1
м
i1 = {cos j , sin j }
п
п
. OM = x i + y j = x1 i1 + y1 j1 Ю
н
п
j
=
{
sin
j
,
cos
j
}
п
о 1
выражение старых координат ( x, y) точки M
через ее новые координаты ( x1 , y1 ) в OX1Y1 . УТС
Y
жx1 ц
жx ц
жcos j - sin j ц
ч
зз ч
зз ч
з
=
Ы X = AX 1 .
ч
ч
ч
з
ч
ч и
ч
з
зиyш
з sin j
cos j шиy1 ш
жcos j - sin j ч
ц T
- 1
з
A= з
.
A
=
A
Ю
ч
ч
зиsin j
cos j ш
A - ортогональная матрица.
Y1
7.10.21
M
y
j
j1
i1
O
i
x
X1
X

82.

Пр. Привести уравнение кривой x 2 - 2 xy + y 2 - 2 x - 2 y + 3 = 0
к каноническому виду и изобразить ее.
1
- 2 p
j = arctg
=
2
1- 1 4
м
п
2
2
п
x
=
x
y1
п
1
п
2
2
Ю п
Ю
н
п
2
2
п
п
y
=
x
+
y1
1
п
2
2
п
о
Ю 2 y - 2 2 x1 + 3 = 0 Ю y =
2
1
2
1
м
п
3 2
п
x
=
x
+
2
Ю п
н1
4
п
п
п
о y1 = y2
Y
Y1
X1
4
Ю
X
0
ж
ц
3 2ч
з
ч
2 зз x1 Ю
ч
зи
4 ч
ш
Y
X 1, X 2
Y2
Ю
Y1
Ю y22 =
3 2 4
0
- уравнение параболы.
X
2 x2 -

83.

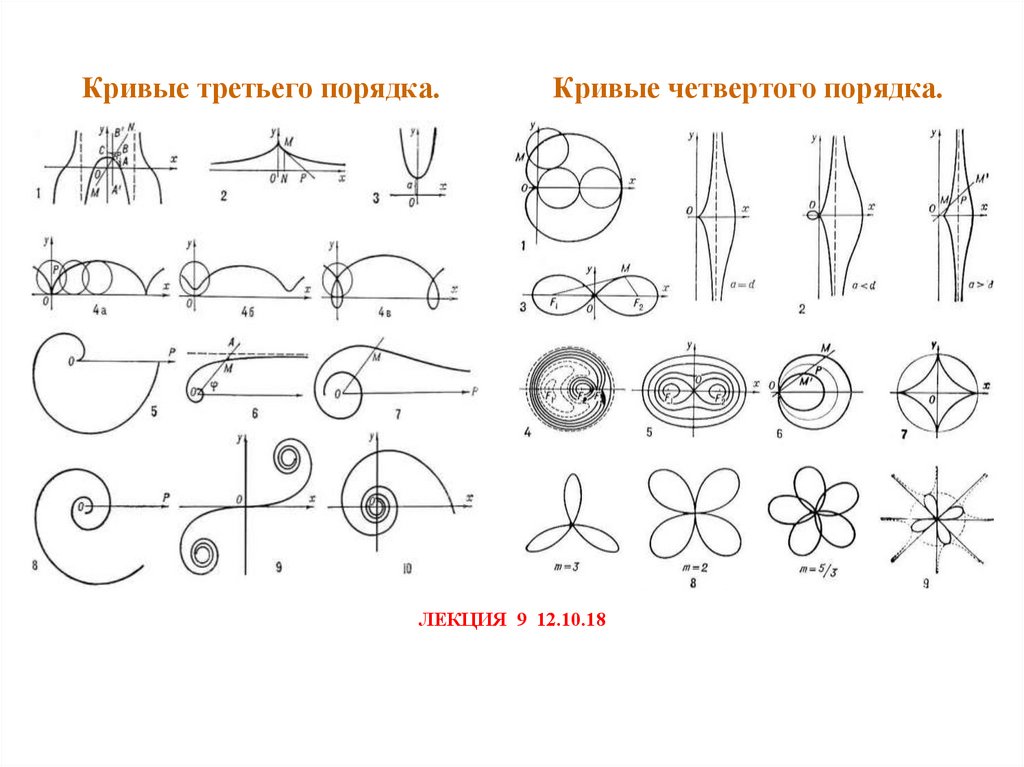
Кривые третьего порядка.
Кривые четвертого порядка.
ЛЕКЦИЯ 9 12.10.18

84.

§ 2.5 Поверхности второго порядка в евклидовом
пространстве V3 . Движение. Квадратичная форма.
Поверхность второго порядка - множество точек в V3 ,
координаты которых удовлетворяют уравнению вида
a11 x2 a22 y 2 a33 z 2 2a12 xy 2a13 xz 2a23 yz b1x b2 y b3 z c 0 ,
b1
x
или в матричной записи X AX BX c 0, где X : y , B : b2 , а
z
b
3
A (aij ) 0 - симметричная матрица.
Пример 1 Эллипсоид – множество
точек в V3 , координаты которых
x2 y 2 z 2
удовлетворяют уравнению 2 2 2 1 .
a
b
c
Отрезки [ a,0], [0, a] OX , [ b,0], [0, b] OY ,
[ c,0], [0, c] OZ - полуоси эллипсоида.
ЛЕКЦИЯ 11.13

85.

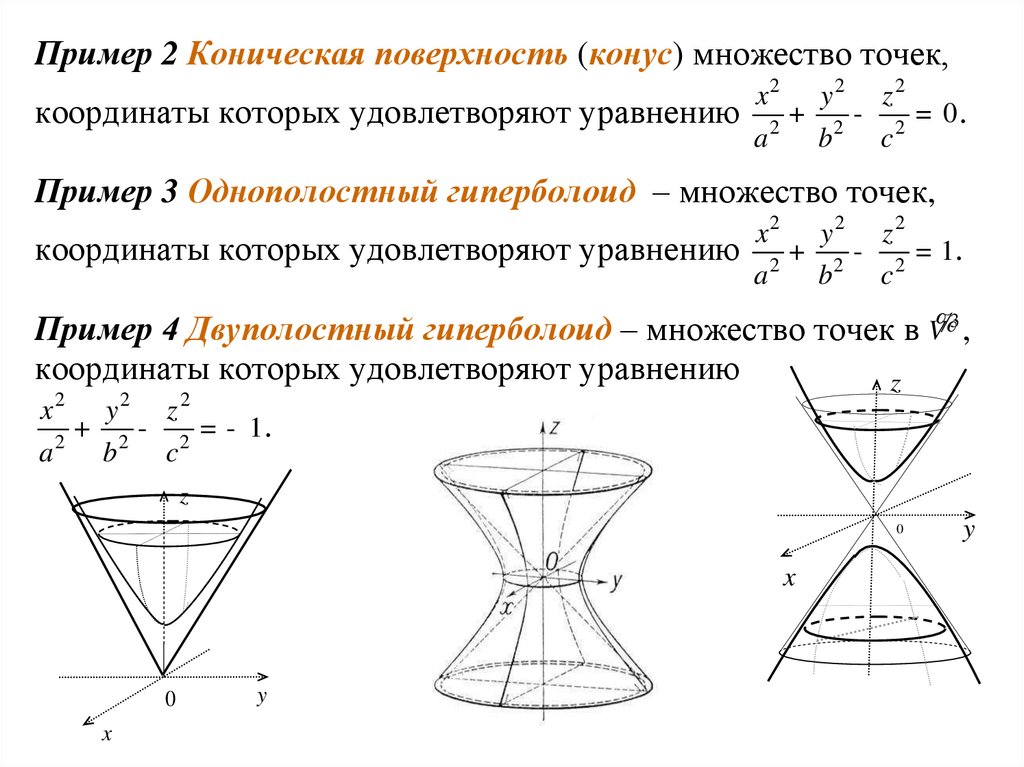
Пример 2 Коническая поверхность (конус) множество точек,
x2 y 2 z 2
координаты которых удовлетворяют уравнению 2 + 2 - 2 = 0 .
a
b
c
Пример 3 Однополостный гиперболоид – множество точек,
x2 y 2 z 2
координаты которых удовлетворяют уравнению 2 + 2 - 2 = 1.
a
b
c
Пример 4 Двуполостный гиперболоид – множество точек в V%3 ,
координаты которых удовлетворяют уравнению
z
x2 y 2 z 2
+ 2 - 2 = - 1.
2
a
b
c
z
0
x
0
x
y
y

86.

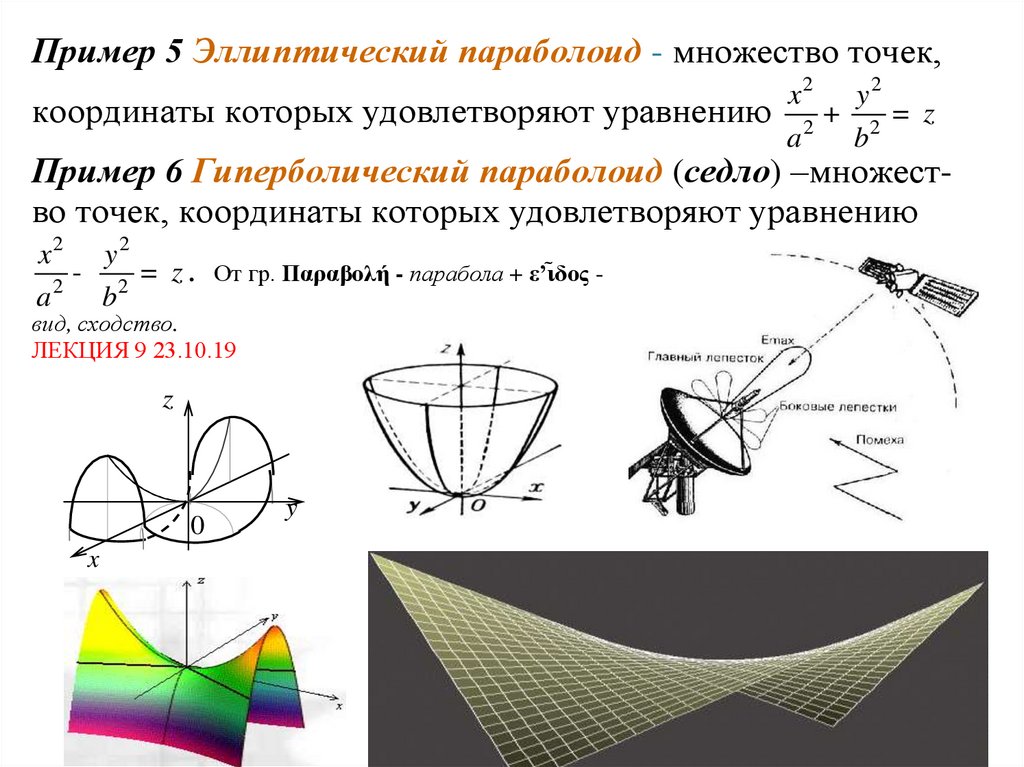
Пример 5 Эллиптический параболоид - множество точек,
x2 y 2
координаты которых удовлетворяют уравнению 2 + 2 = z
a
b
Пример 6 Гиперболический параболоид (седло) –множество точек, координаты которых удовлетворяют уравнению
x2 y 2
- 2 = z . От гр. Παραβολή - парабола + ε’ι̃δος 2
a
b
вид, сходство.
ЛЕКЦИЯ 9 23.10.19
z
0
x
y

87.

Пример 7 Эллиптический цилиндр - множество точек, координаты кото
рых удовлетворяют уравнению
x2
y2
+
= 1.
a 2 b2
z
y
x
Шарообразную форму здания,
расположенного в густонаселенном районе
Токио, образуют 24 овальных кольца,
закрепленных вокруг полого
эллиптического цилиндра.
ЛЕКЦИЯ 11 19.10.14

88.

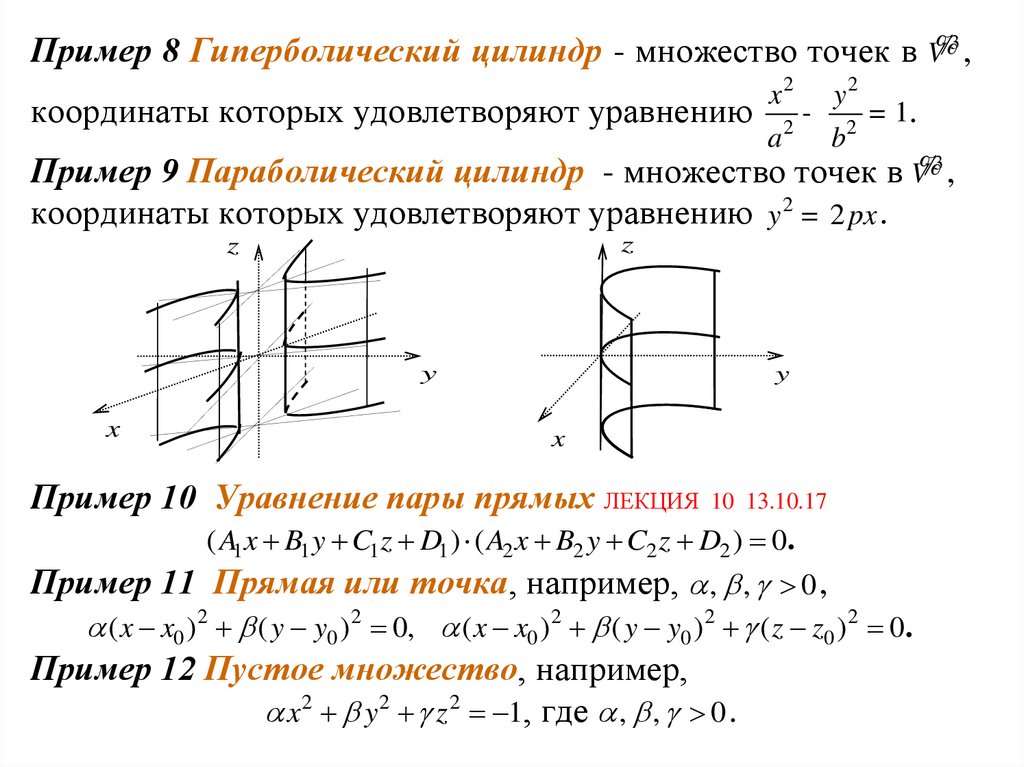
Пример 8 Гиперболический цилиндр - множество точек в V%3 ,
x2 y 2
координаты которых удовлетворяют уравнению 2 - 2 = 1.
a
b
Пример 9 Параболический цилиндр - множество точек в V%3 ,
координаты которых удовлетворяют уравнению y 2 = 2 px .
z
z
y
y
x
x
Пример 10 Уравнение пары прямых ЛЕКЦИЯ 10 13.10.17
( A1x B1 y C1z D1 ) ( A2 x B2 y C2 z D2 ) 0 .
Пример 11 Прямая или точка, например, , , 0 ,
( x x0 )2 ( y y0 )2 0, ( x x0 )2 ( y y0 )2 ( z z0 )2 0 .
Пример 12 Пустое множество, например,
x2 y 2 z 2 1, где , , 0 .