Презентация по математике на тему _Объём пирамиды_ (11 класс) (2)

1.

2. Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в

плоскости основания –
вершины пирамиды и
треугольников боковых граней.

3.

Термин “пирамида” заимствован
из греческого “пирамис” или “пирамидос”. Греки в
свою очередь позаимствовали это слово, как
полагают, из египетского языка. В папирусе Ахмеса
встречается слово “пирамус” в смысле ребра
правильной пирамиды. Другие считают, что термин
берет свое начало от форм хлебцев в Древней
Греции “пирос” - рожь). В связи с тем, что форма
пламени иногда напоминает образ пирамиды,
некоторые средневековые ученые считали, что
термин происходит от греческого слова “пир” огонь. Вот почему в некоторых учебниках геометрии
XVI в. пирамида названа “огнеформное тело”.

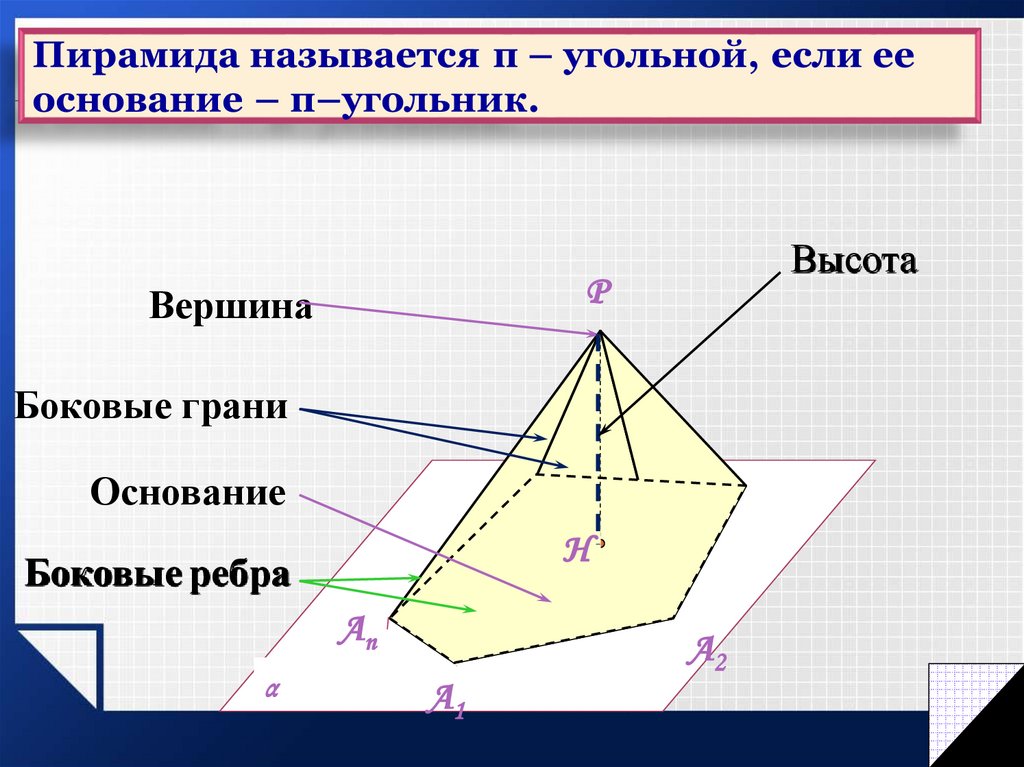
4.

Высота
P
Вершина
Боковые грани
Основание
H
Боковые ребра
Аn
α
А2
А1

5. Пирамиды

Треугольная
пирамида
(тетраэдр)
Четырехугольная
пирамида
Шестиугольная
пирамида

6.

Пирамида называется правильной, если ее
основание - правильный многоугольник , а
отрезок, соединяющий вершину пирамиды с
центром основания, является ее высотой.
P
h
O
Аn
А1
А3
А2

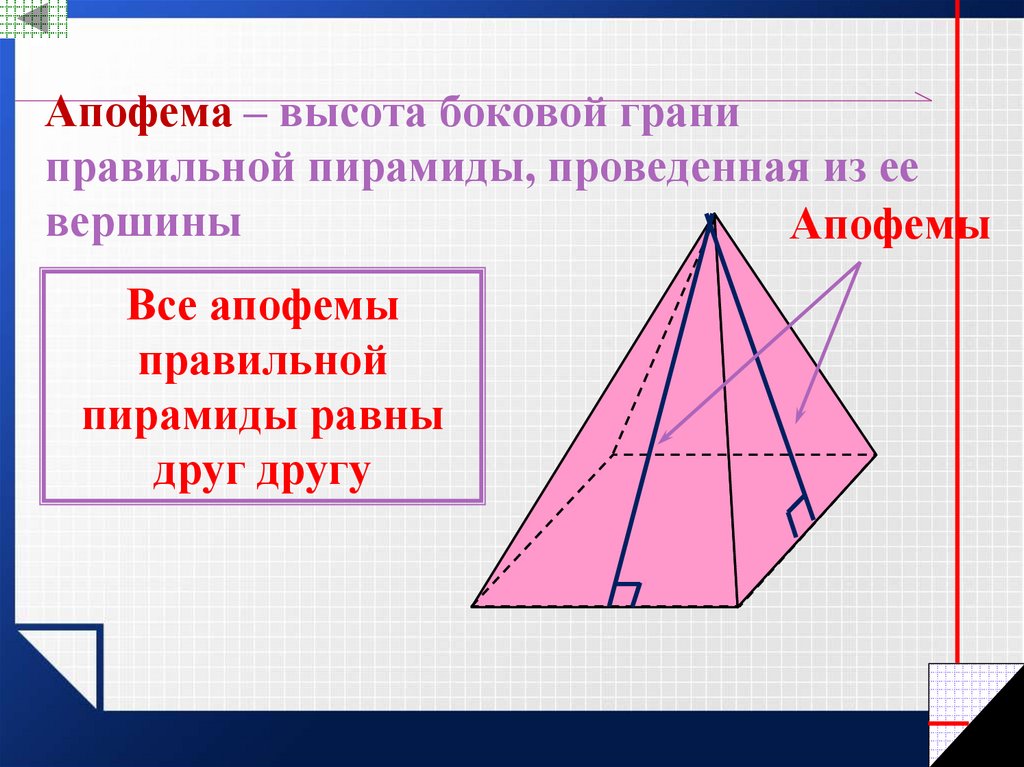
7. Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины

Апофемы
Все апофемы
правильной
пирамиды равны
друг другу

8. Диагональное сечение пирамиды – сечение плоскостью, проходящей через два не соседних боковых ребра

9.

10. Площадь пирамиды

Sполн. = Sбок. + Sосн.
Sбок.
Sосн.

11.

1
S бок. Pосн. h
2
H
h

12.

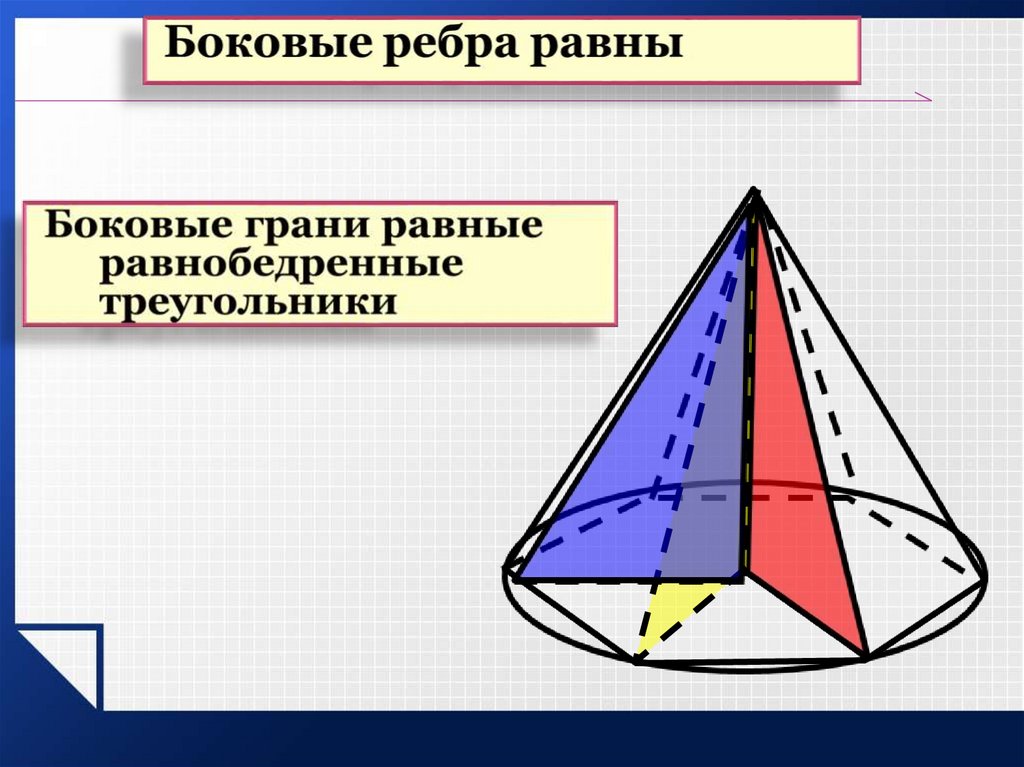
Свойства пирамиды:
У правильной пирамиды:
боковые ребра равны;
боковые грани являются
равными равнобедренными
треугольниками;
апофемы равны;
площадь боковой
поверхности правильной
пирамиды равна половине
произведения периметра на
апофему.

13.

Свойства пирамиды:
если боковые ребра пирамиды
равны (или составляют равные
углы с плоскостью основания), то
вершина пирамиды проецируется в
центр окружности, описанной
около основания.
если двугранные углы при
основании пирамиды равны (или
равны высоты боковых граней,
проведенные из вершины
пирамиды), то вершина пирамиды
проецируется в центр окружности,
вписанной в основание пирамиды.

14.

1
V = Sосн.∙h
3

15.

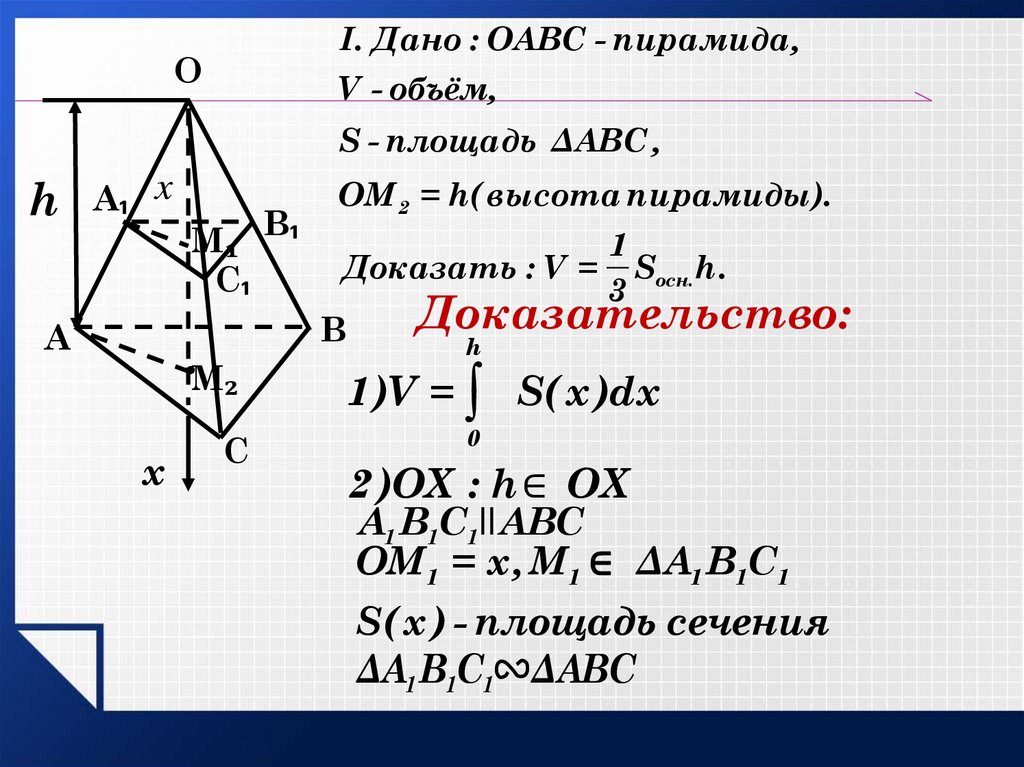
I. Дано : ОАВС - пирамида,
V - объём,
O
S - площадь ΔАВС ,
h
А₁ x
М₁
С₁
В₁
ОМ 2 = h( высота пирамиды).
1
Доказать : V = Sосн. h.
3
В
А
М₂
х
С
Доказательство:
h
1 )V = ∫ S( x )dx
0
2 )OX : h ∈ OX
А1 В1С1IIАВС
ОМ 1 = х , М1 ∈ ΔА1 В1С1
S( x ) - площадь сечения
ΔА1 В1С1 ΔАВС

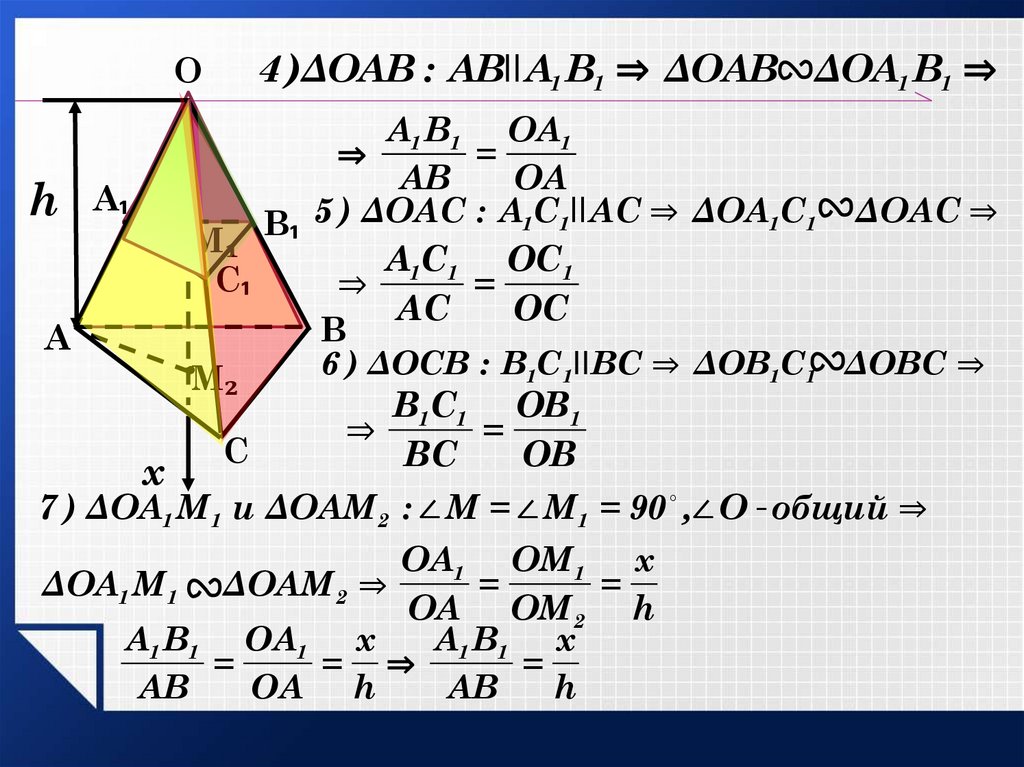
16.

O
h
А₁
А
х
4 )ΔОАВ : АВIIА1 В1 ⇒ ΔОАВ ΔОА1 В1 ⇒
А1 В1 ОА1
⇒
=
АВ
ОА
В₁ 5 ) ΔОАС : А1С1II АС ⇒ ΔОА1С1 ΔОАС ⇒
М₁
А1С1 ОС1
С₁
⇒
=
АС
ОС
В
6 ) ΔОСВ : В1С1II ВС ⇒ ΔОВ1С1 ΔОВС ⇒
М₂
В1С1 ОВ1
⇒
=
С
ВС
ОВ
7 ) ΔОА1 М 1 и ΔОAМ 2 : ∠ М = ∠ М 1 = 90 ,∠ О - общий ⇒
ОА1 ОМ 1 х
ΔОА1 М 1 ΔОAМ 2 ⇒
=
=
ОА ОМ 2 h
А1 В1 ОА1 х
А1 В1 х
=
= ⇒
=
АВ
ОА h
АВ
h

17.

O
h
А1С1 х В1С1 х
Аналогично :
= ;
=
АС
h ВС
h
ΔАВС
В₁
А₁ М₁
С₁
А
М₂
х
С
х
ΔА1 В1С1 : - коэффициен т подобия
h
S( x )
x 2
S 2
8)
= ( ) ⇒ S( x ) = 2 x
S
h
h
h
h
В
S 2
V = ∫ S( x )dx = ∫
2 x dx =
h
0
0
1
S
x
S
= Sh
= 2 ∫ x 2 dx =
2
h 0
h
30 3
h
3 h

18.

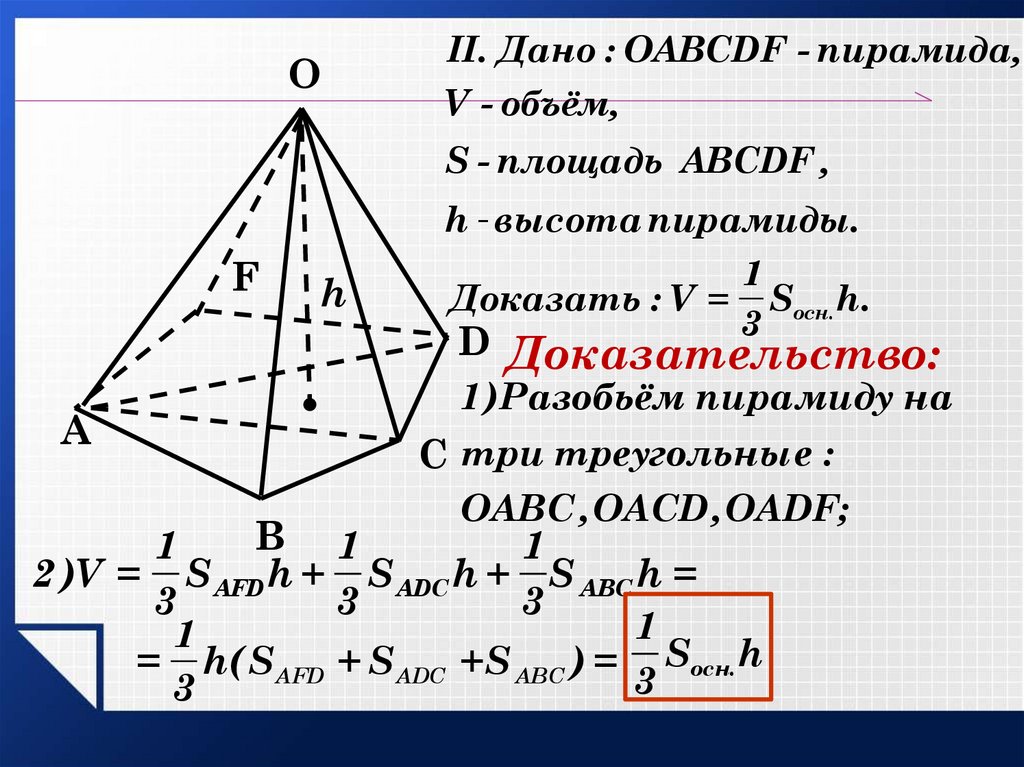
О
II. Дано : ОАВСDF - пирамида,
V - объём,
S - площадь АВСDF ,
F
h
h - высота пирамиды.
1
Доказать : V = Sосн. h.
3
D Доказательство:
А
1 )Разобьём пирамиду на
С три треугольны е :
ОАВС , ОАСD , ОАDF;
В 1
1
1
2 )V = SAFD h + SADC h + S ABC h =
3
3
3
1
1
= h( S AFD + S ADC +S ABC ) = Sосн. h
3
3

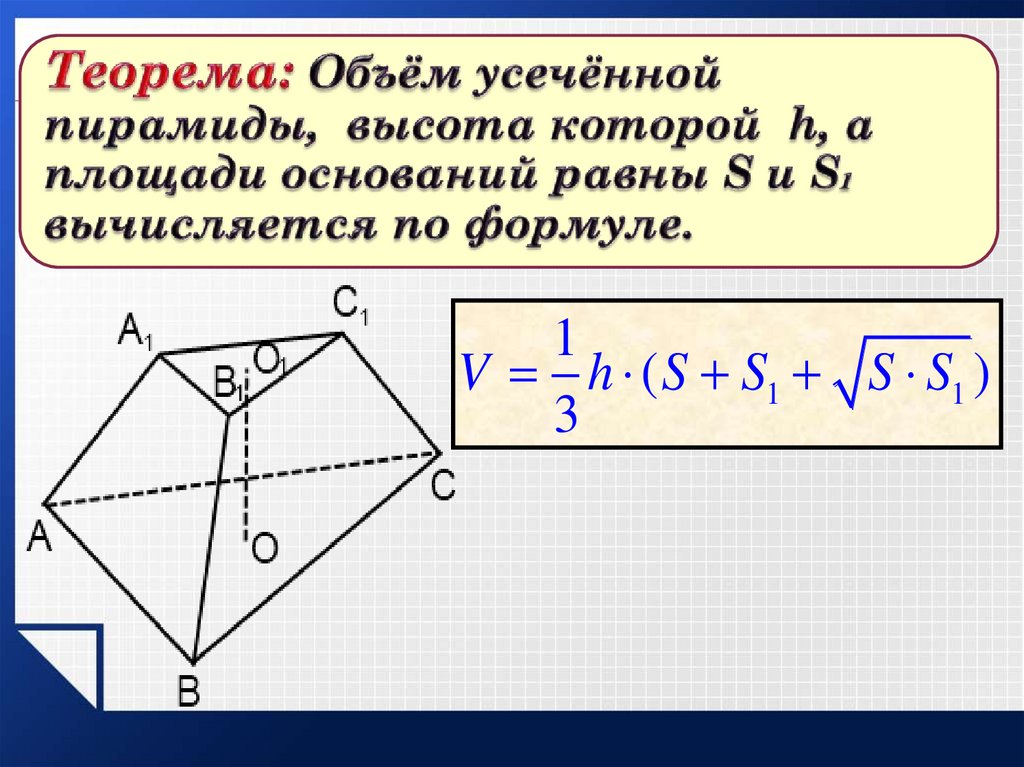
19.

1
V h ( S S1 S S1 )
3

20.

Объем усеченной пирамиды
будем рассматривать как
разность объемов полной
пирамиды и той, что отсечена
от нее плоскостью,
параллельной основанию

21.

Объем полной
1
V Sh
пирамиды
3
x
S1
h
S
1
1
1
1
1
V Sh Sx S1 x Sh x( S S1 )
3
3
3
3
3
S (h x) 2
S1
x2
h S1
x
S S1
(1)
S x S1 h S1 x
S x S1 x S1 h
Подставляем в уравнение 1
h S1
1
1
V Sh ( S S1 )
3
3
S S1
h S1
1
1
Sh ( S S1 )( S S1 )
3
3
S S1
1
1
1
1
Sh S1h h SS1 h( S S1 SS1 )
3
3
3
3

22.

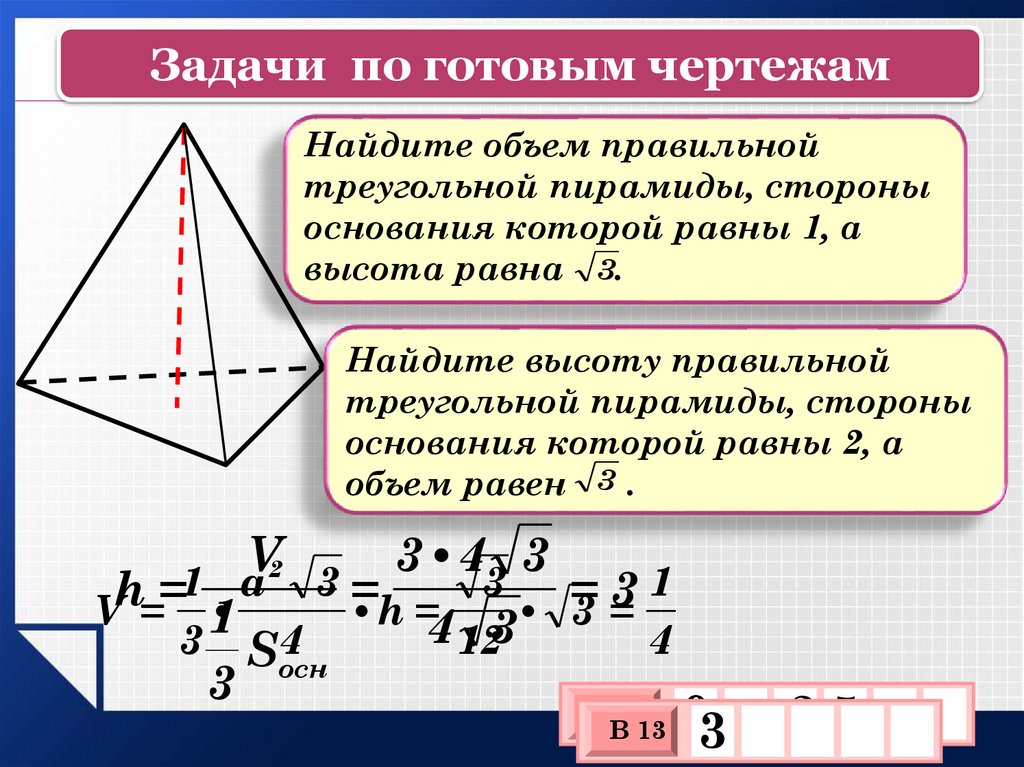
Задачи по готовым чертежам
Найдите объем правильной
треугольной пирамиды, стороны
основания которой равны 1, а
высота равна 3.
Найдите высоту правильной
треугольной пирамиды, стороны
основания которой равны 2, а
объем равен 3 .
V2
3 •4 3
1 a 3=
3
1
h
=
=
3
V= 1
• h =4 3• 3 =
3 S4
12
4
3 осн
В 13
25
В 13 03 ,
3
1 03 х
10 х
х
х

23.

Задачи по готовым чертежам
В правильной четырехугольной
пирамиде высота равна 6, сторона
основания равна 10. Найдите ее
объем.
.
В правильной четырехугольной
пирамиде высота равна 6, боковое
ребро равно 10. Найдите ее объем.
Н
450
1
2
2 VAB
=
10
•6= 8
= 200
AB
2
=
2
16 3
AB
сos45 =
AC
1
2
V = 8 2 •6 = 256
3
0
(
)
В 13
В 13
22 05 06
3
1 03 х
10 х
х
х

24.

Задачи (база)
Сторона основания правильной
треугольной пирамиды равна 6, а
V =18 с плоскостью
боковое ребро образует
основания угол 450. Найдите объем
пирамиды.
Высота правильной треугольной
пирамиды равна 4 3 , а боковая грань
V = 192 основания угол
образует с плоскостью
600. Найдите объем пирамиды.

25.

Задачи (профиль)
Объем треугольной пирамиды SABC,
являющейся частью правильной
V = 48
шестиугольной пирамиды SABCDEF, равен 8.
Найдите объем шестиугольной пирамиды.
От треугольной пирамиды, объем которой
равен 12, отсечена треугольная пирамида
плоскостью, проходящей через вершину
=3 основания.
пирамиды и среднююV
линию
Найдите объем отсеченной треугольной
пирамиды.

26.

27. В презентации использованы материалы сайта Савченко Е.М.