практика 10 классич метод 1 порядка

1.

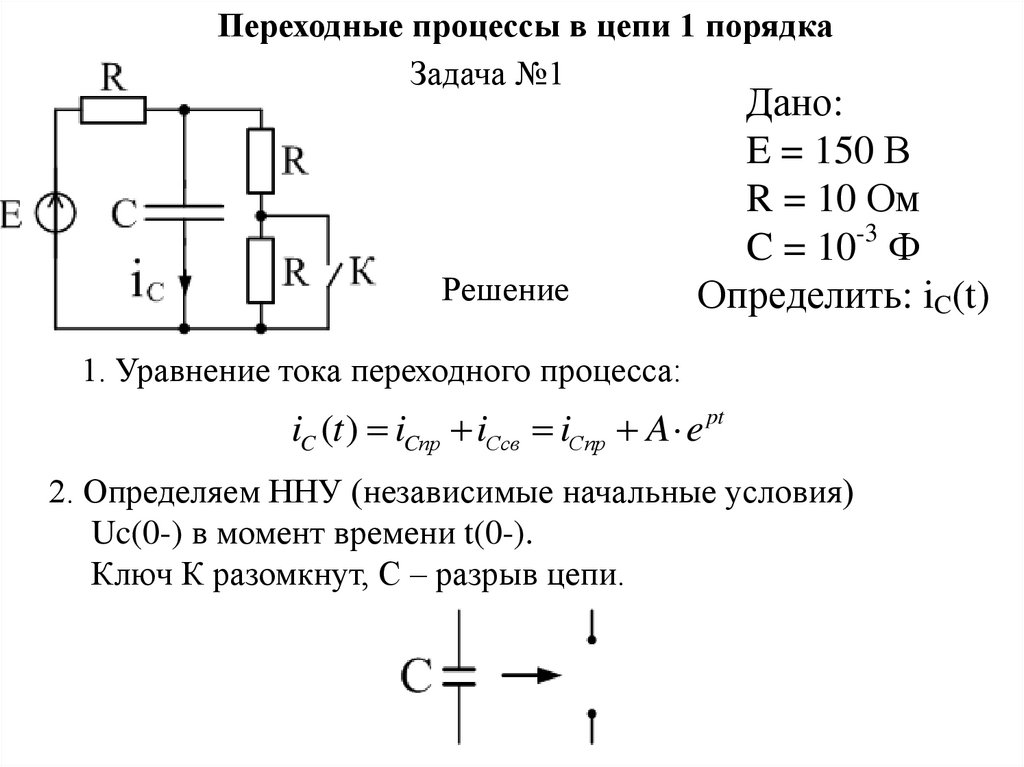
Переходные процессы в цепи 1 порядка
Задача №1
Решение
Дано:
E = 150 В
R = 10 Ом
C = 10-3 Ф
Определить: iC(t)
1. Уравнение тока переходного процесса:
iC (t ) iCпр iCсв iCпр A e pt
2. Определяем ННУ (независимые начальные условия)
Uc(0-) в момент времени t(0-).
Ключ К разомкнут, С – разрыв цепи.

2.

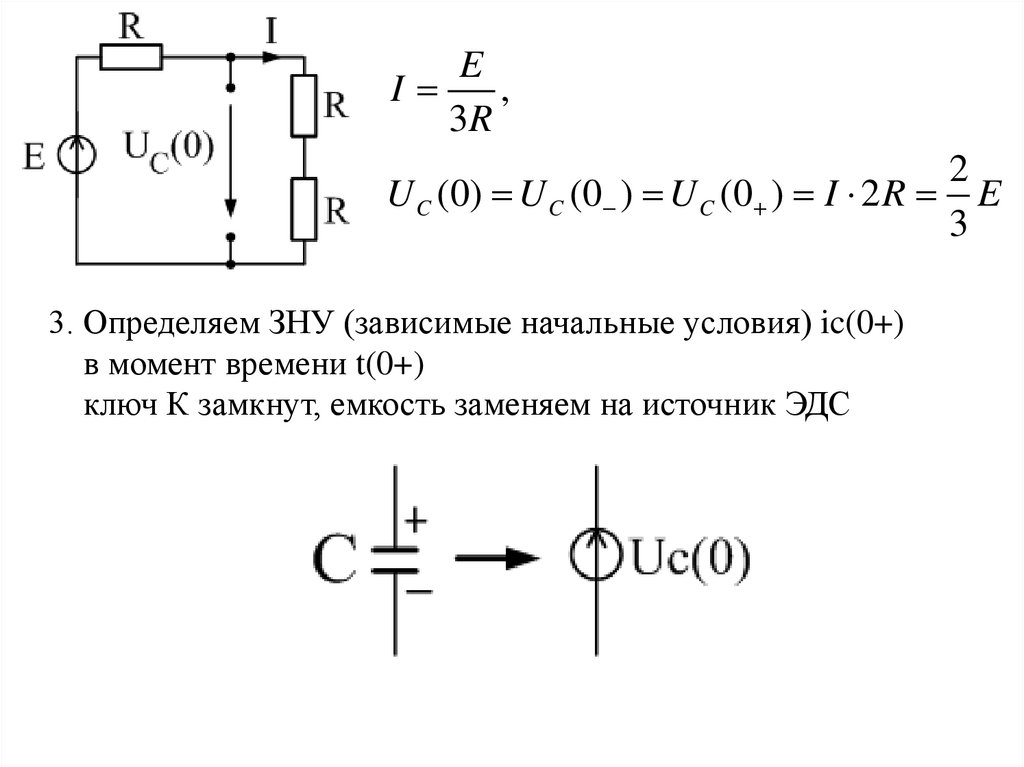
E
I
,
3R
2
U C (0) U C (0 ) U C (0 ) I 2 R E
3
3. Определяем ЗНУ (зависимые начальные условия) ic(0+)
в момент времени t(0+)
ключ К замкнут, емкость заменяем на источник ЭДС

3.

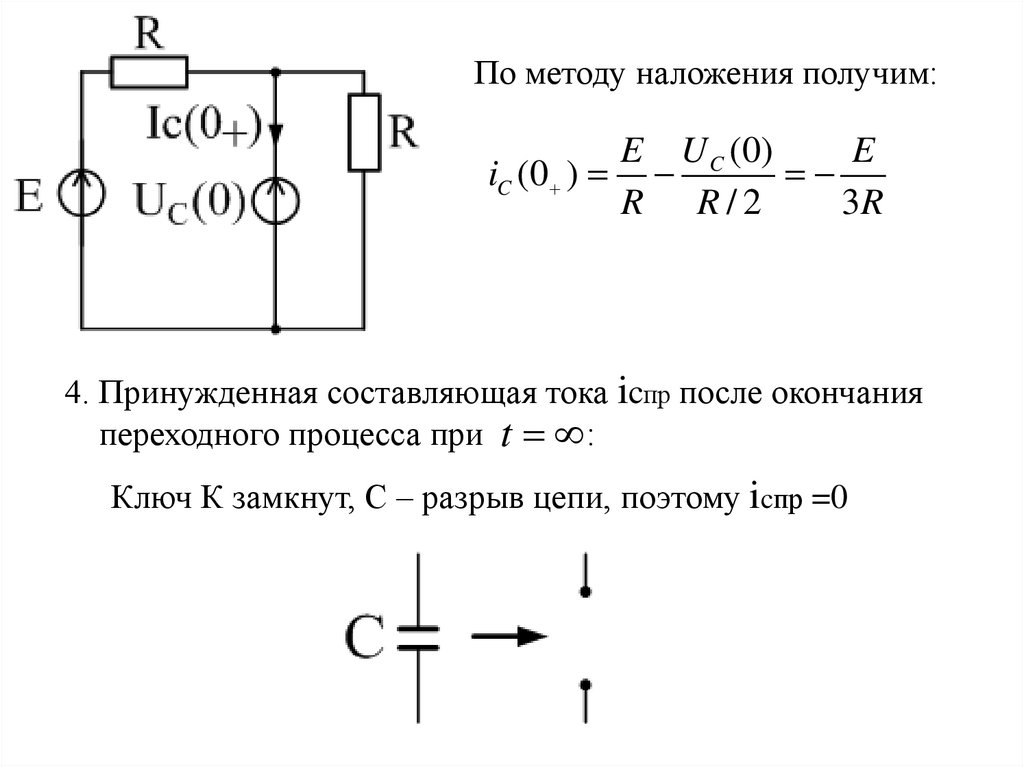
По методу наложения получим:
E U C (0)
E
iC (0 )
R R/2
3R
4. Принужденная составляющая тока icпр после окончания
переходного процесса при t :
Ключ К замкнут, С – разрыв цепи, поэтому icпр =0

4.

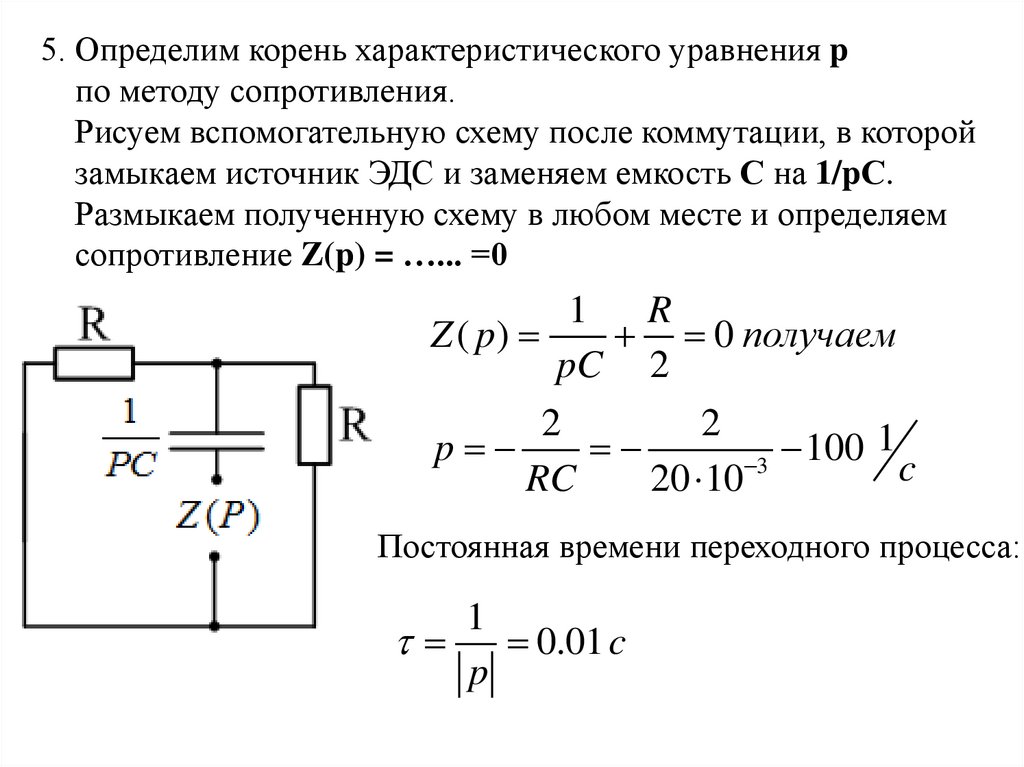
5. Определим корень характеристического уравнения p
по методу сопротивления.
Рисуем вспомогательную схему после коммутации, в которой
замыкаем источник ЭДС и заменяем емкость С на 1/pС.
Размыкаем полученную схему в любом месте и определяем
сопротивление Z(p) = …... =0
1
R
Z ( p)
0 получаем
pC 2
2
2
1
p
100
c
RC
20 10 3
Постоянная времени переходного процесса:
1
0.01 c
p

5.

Уравнение для тока переходного процесса в момент времени t=0+
iC (0 ) iCпр A
потому что e p 0 1
6. Определяем постоянную интегрирования
E
так как iCпр 0, получим : A iC (0 ) iCпр
3R
7. Ответ:
t
E
E
iC (t ) iCпр A e pt
e pt
e
3R
3R
t
150 100t
e
5e 100t 5e 0.01 A
3 10
Длительность переходного процесса
t П 5 0.05 с

6.

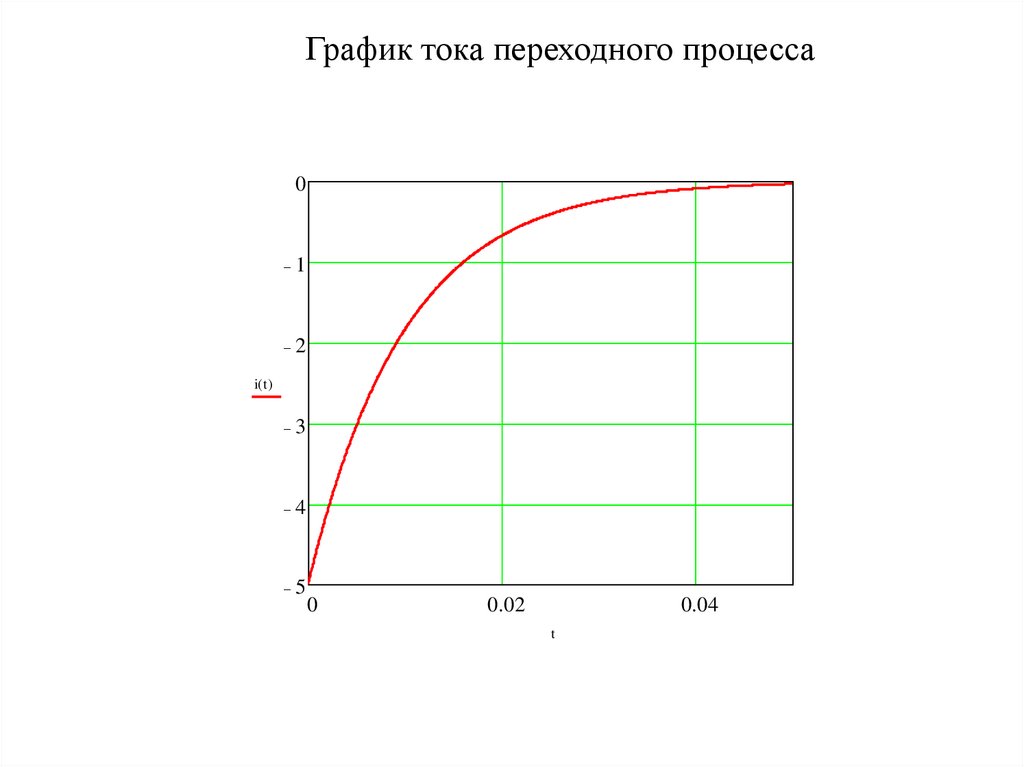
График тока переходного процесса
0
1
2
i( t )
3
4
5
0
0.02
0.04
t

7.

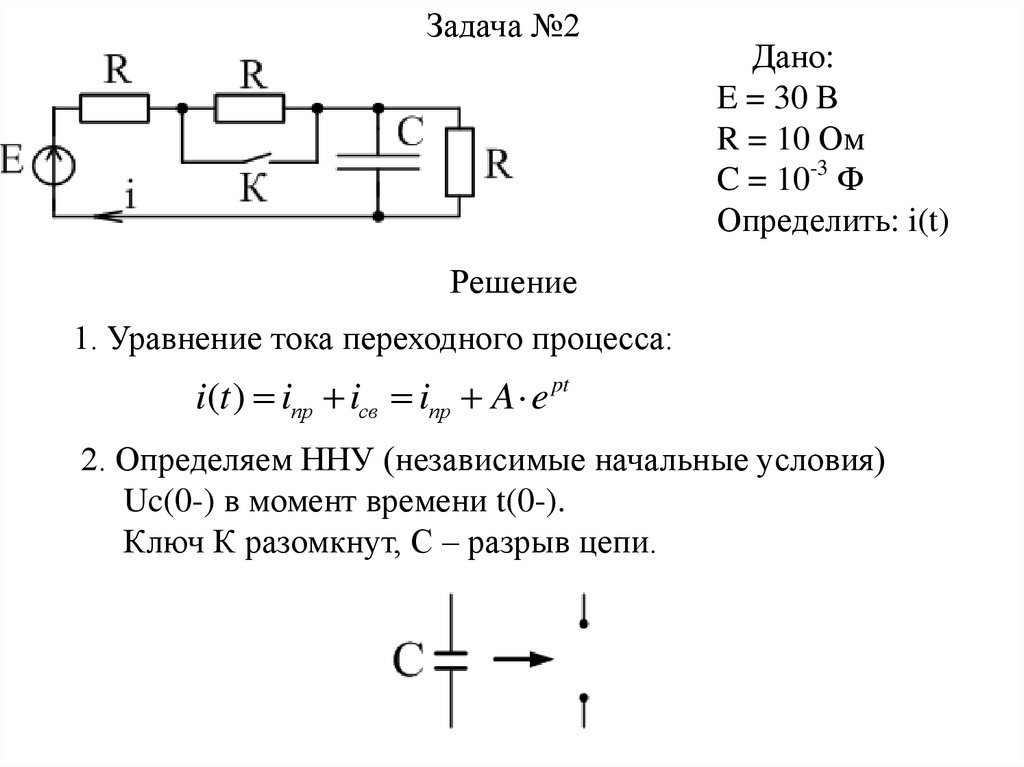
Задача №2
Дано:
E = 30 В
R = 10 Ом
C = 10-3 Ф
Определить: i(t)
Решение
1. Уравнение тока переходного процесса:
i(t ) iпр iсв iпр A e pt
2. Определяем ННУ (независимые начальные условия)
Uc(0-) в момент времени t(0-).
Ключ К разомкнут, С – разрыв цепи.

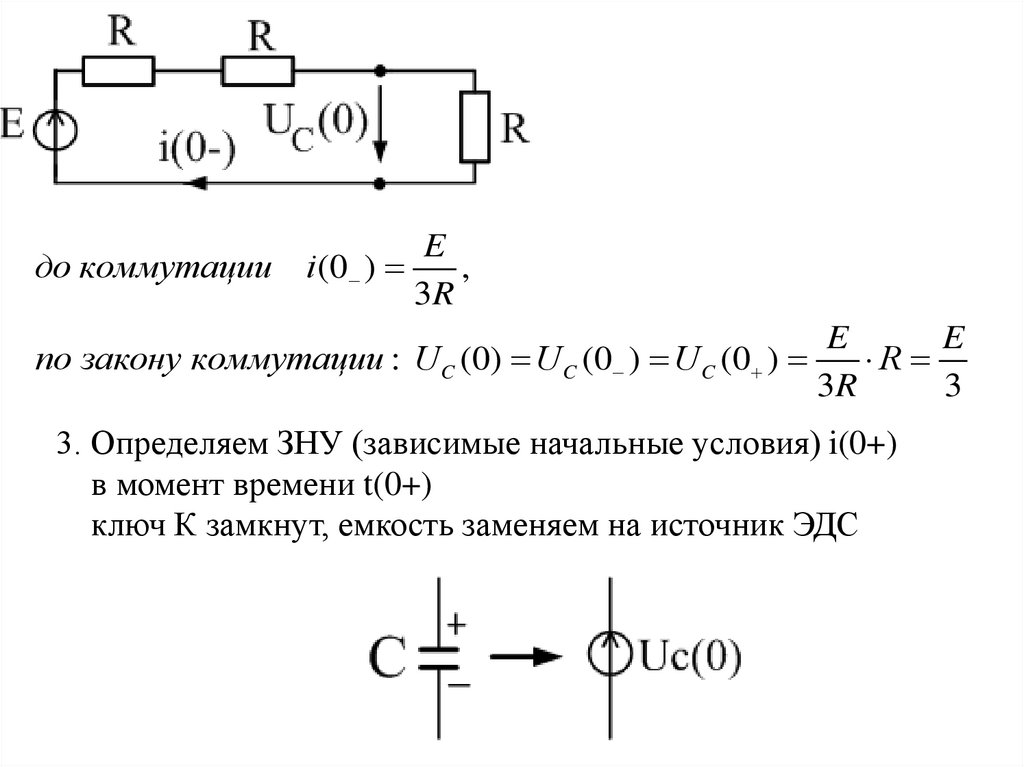
8.

E
до коммутации i (0 )
,
3R
E
E
по закону коммутации : U C (0) U C (0 ) U C (0 )
R
3R
3
3. Определяем ЗНУ (зависимые начальные условия) i(0+)
в момент времени t(0+)
ключ К замкнут, емкость заменяем на источник ЭДС

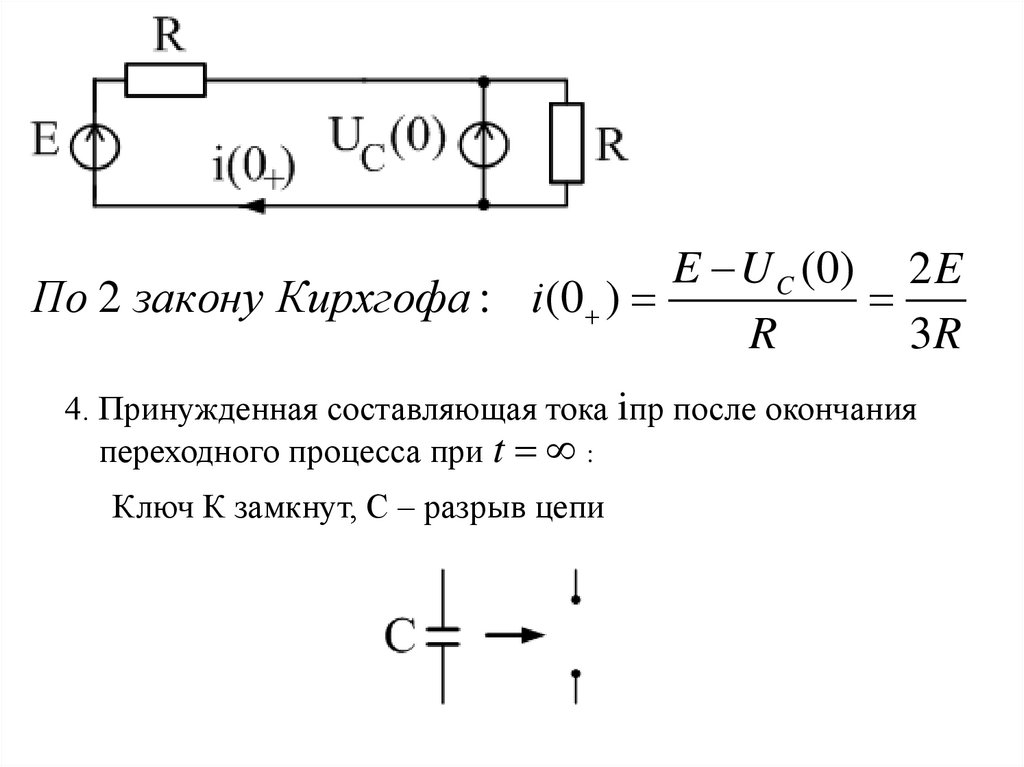
9.

E U C (0) 2 E
По 2 закону Кирхгофа : i (0 )
R
3R
4. Принужденная составляющая тока iпр после окончания
переходного процесса при t :
Ключ К замкнут, С – разрыв цепи

10.

E
iпр
2R
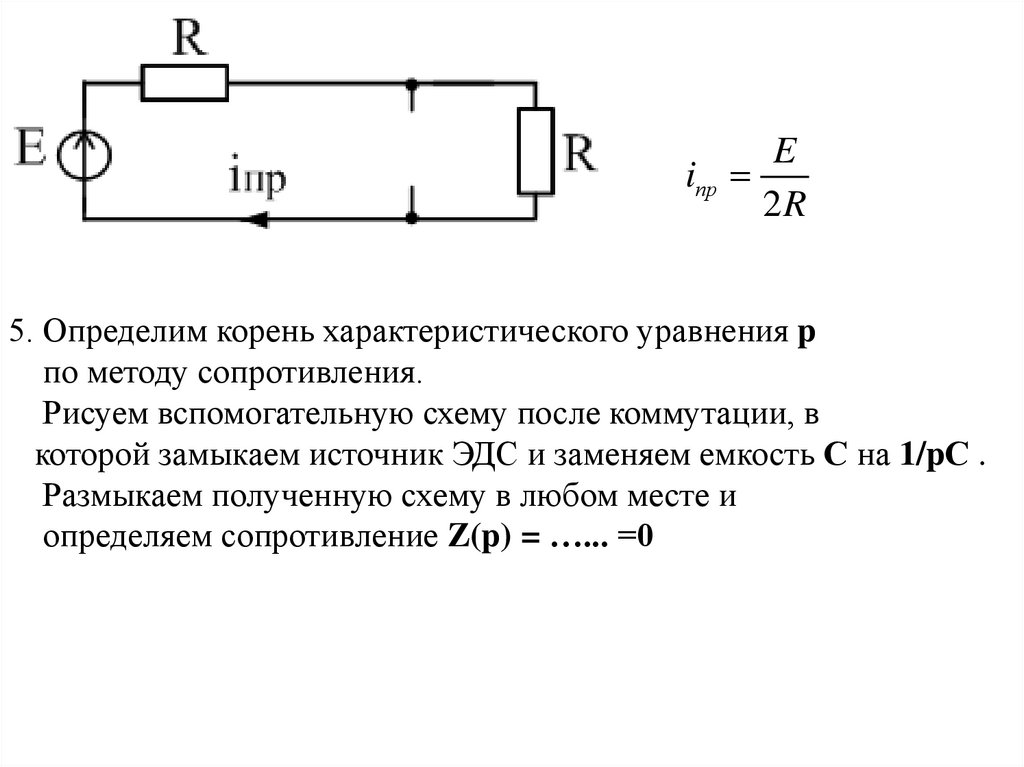
5. Определим корень характеристического уравнения p
по методу сопротивления.
Рисуем вспомогательную схему после коммутации, в
которой замыкаем источник ЭДС и заменяем емкость С на 1/pС .
Размыкаем полученную схему в любом месте и
определяем сопротивление Z(p) = …... =0

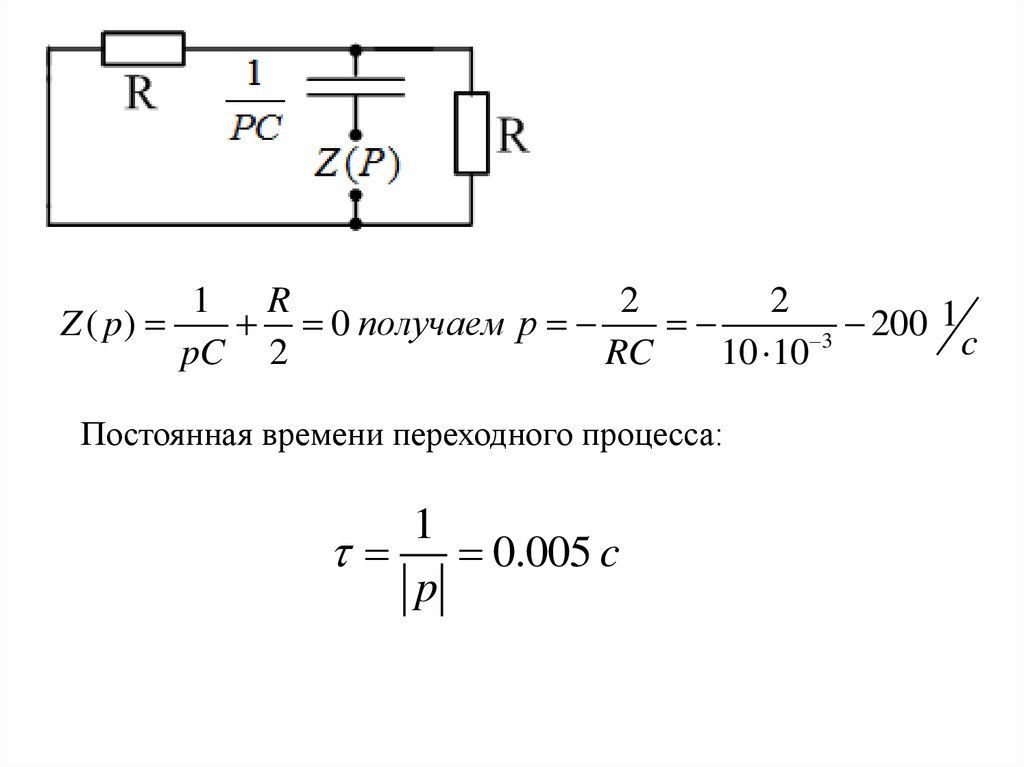
11.

1
R
2
2
1
Z ( p)
0 получаем p
200
c
pC 2
RC
10 10 3
Постоянная времени переходного процесса:
1
0.005 c
p

12.

Уравнение для тока переходного процесса в момент времени t=0+
i(0 ) iпр A
потому что e p 0 1
6. Определяем постоянную интегрирования
2E E
E
A i (0 ) iпр
3R 2 R 6 R
7. Ответ:
t
E
E pt
i (t ) iпр A e
e 1.5 0.5e 200t 1.5 0.5e A,
2R 6R
где 0.005 с
pt
Длительность переходного процесса
t П 5 0.025 с

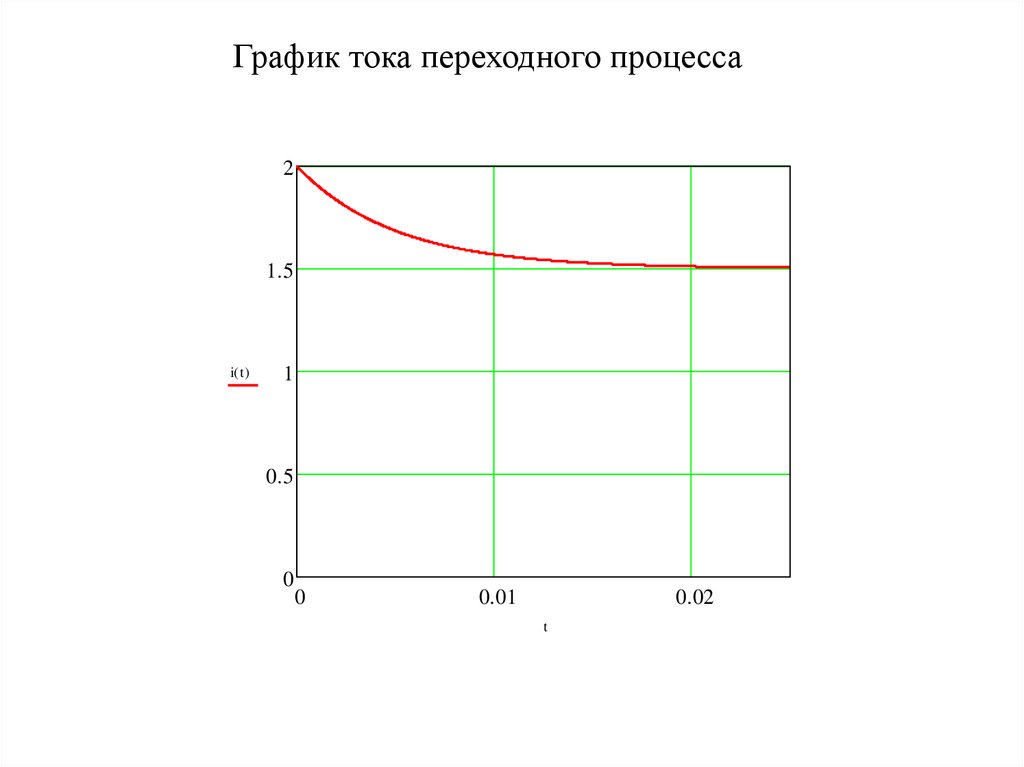
13.

График тока переходного процесса
2
1.5
i( t )
1
0.5
0
0
0.01
0.02
t

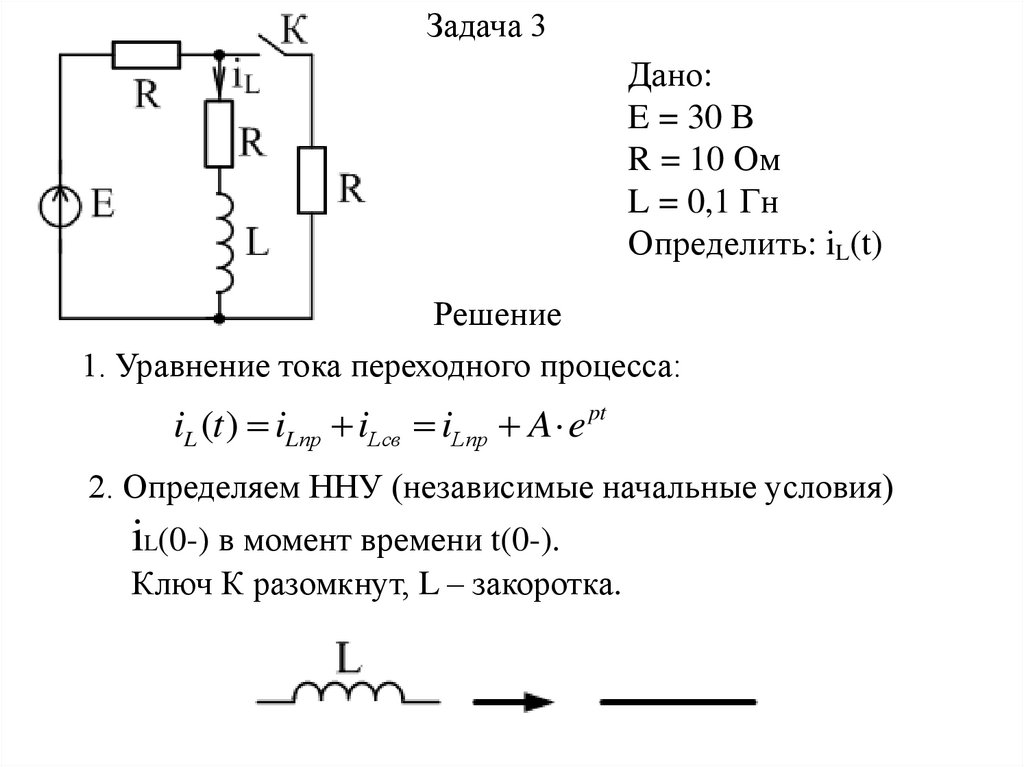
14.

Задача 3
Дано:
E = 30 В
R = 10 Ом
L = 0,1 Гн
Определить: iL(t)
Решение
1. Уравнение тока переходного процесса:
iL (t ) iLпр iLсв iLпр A e pt
2. Определяем ННУ (независимые начальные условия)
iL(0-) в момент времени t(0-).
Ключ К разомкнут, L – закоротка.

15.

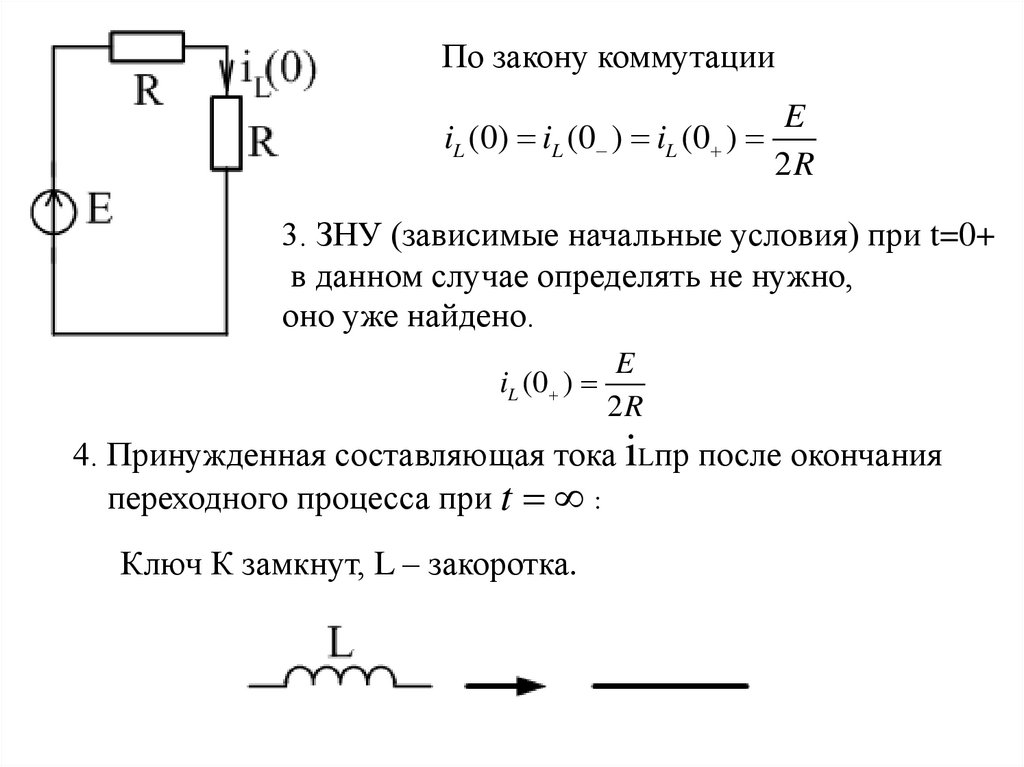
По закону коммутации
E
iL (0) iL (0 ) iL (0 )
2R
3. ЗНУ (зависимые начальные условия) при t=0+
в данном случае определять не нужно,
оно уже найдено.
E
iL (0 )
2R
4. Принужденная составляющая тока iLпр после окончания
переходного процесса при t :
Ключ К замкнут, L – закоротка.

16.

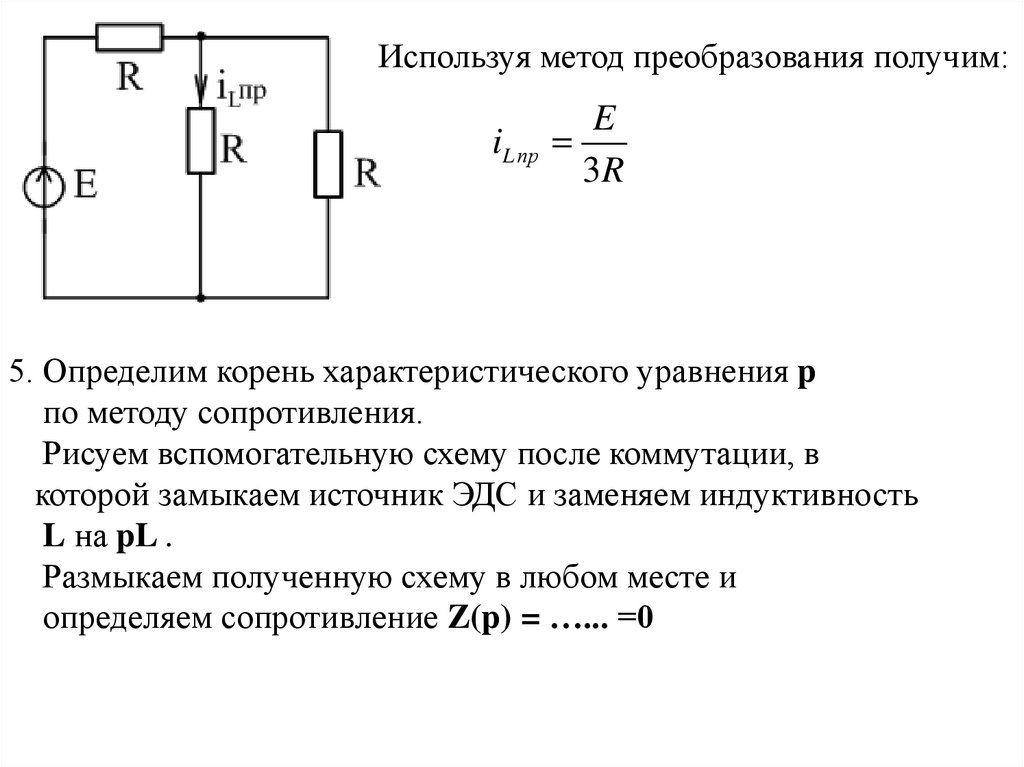
Используя метод преобразования получим:
E
iL пр
3R
5. Определим корень характеристического уравнения p
по методу сопротивления.
Рисуем вспомогательную схему после коммутации, в
которой замыкаем источник ЭДС и заменяем индуктивность
L на pL .
Размыкаем полученную схему в любом месте и
определяем сопротивление Z(p) = …... =0

17.

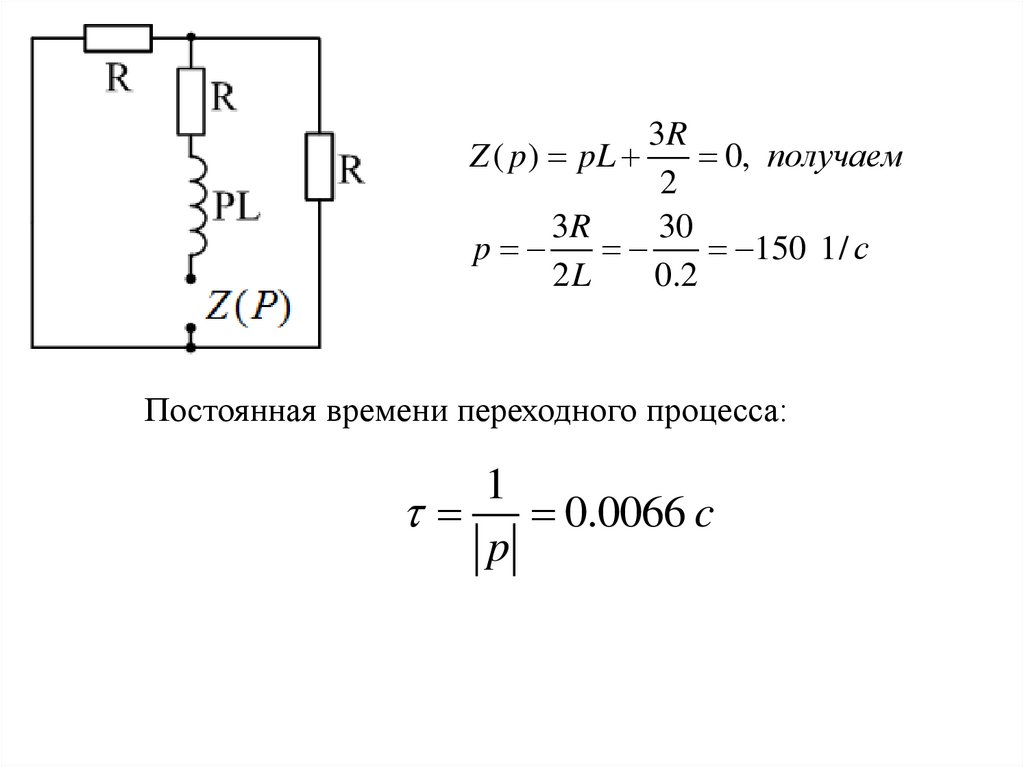
3R
Z ( p) pL
0, получаем
2
3R
30
p
150 1/ с
2L
0.2
Постоянная времени переходного процесса:
1
0.0066 c
p

18.

Уравнение для тока переходного процесса в момент времени t=0+
iL (0 ) iLпр A
потому что e p 0 1
6. Определяем постоянную интегрирования
7. Ответ:
E
E
E
A iL (0 ) iLпр
2 R 3R 6 R
t
E
E pt
iL (t ) iLпр A e
e 1 0.5e 150t 1 0.5e A,
3R 6 R
где 0.0066 с
pt
Длительность переходного процесса
t П 5 0.033 с

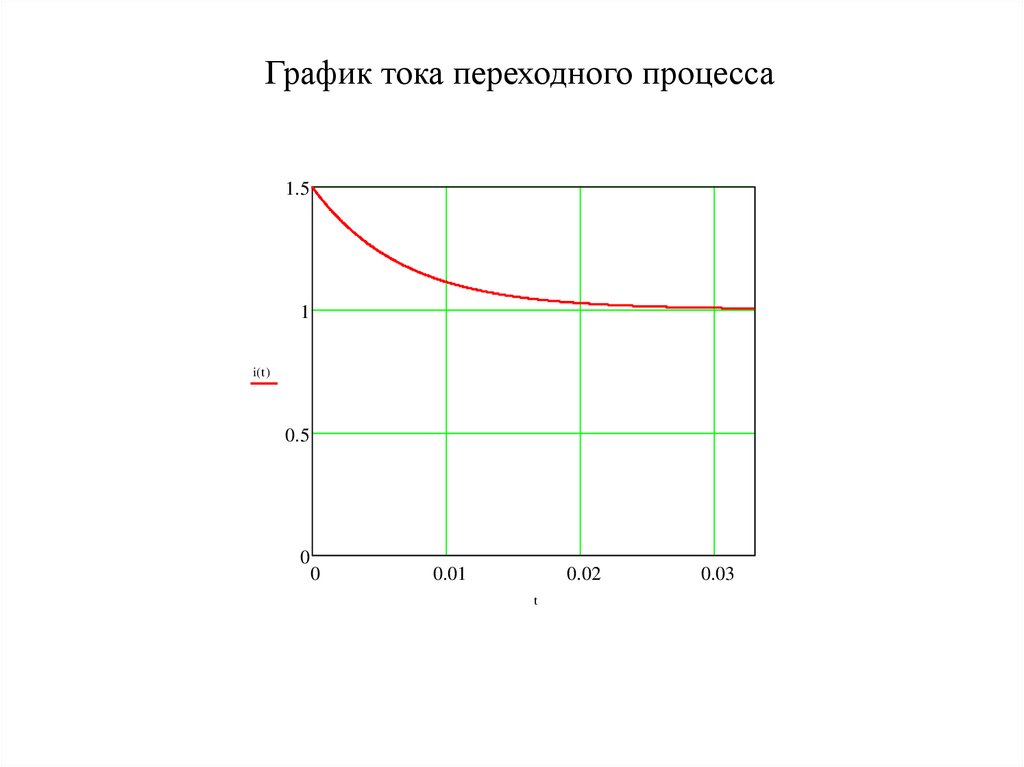
19.

График тока переходного процесса
1.5
1
i( t )
0.5
0
0
0.01
0.02
t
0.03

20.

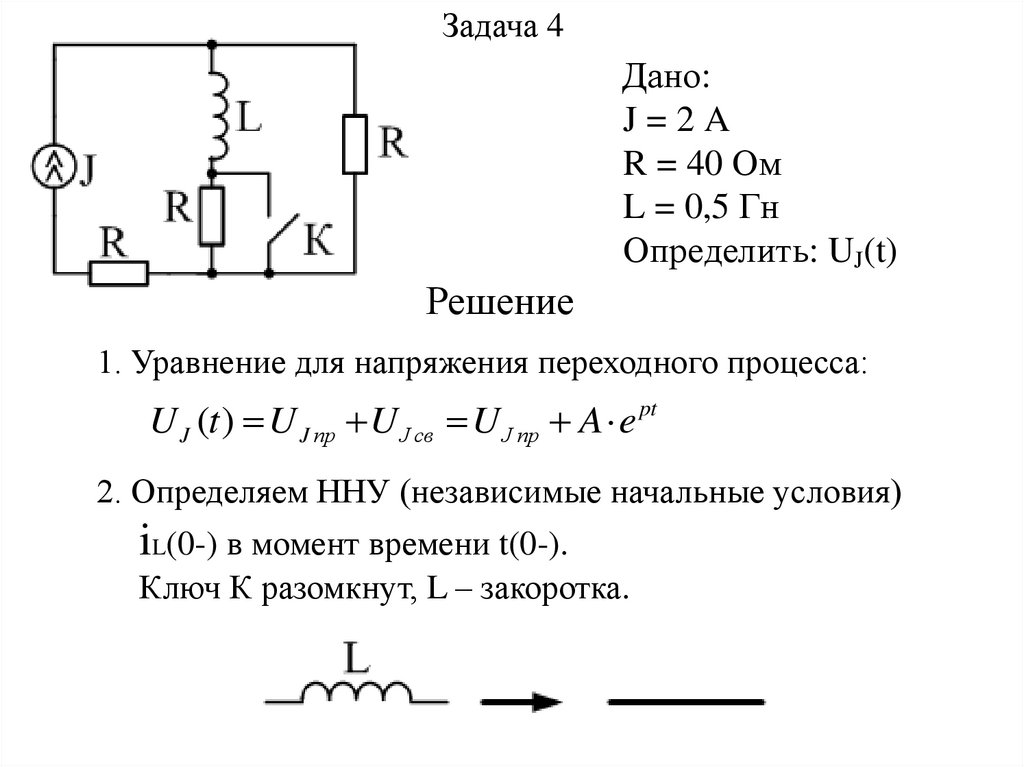
Задача 4
Дано:
J=2A
R = 40 Ом
L = 0,5 Гн
Определить: UJ(t)
Решение
1. Уравнение для напряжения переходного процесса:
U J (t ) U J пр U J св U J пр A e pt
2. Определяем ННУ (независимые начальные условия)
iL(0-) в момент времени t(0-).
Ключ К разомкнут, L – закоротка.

21.

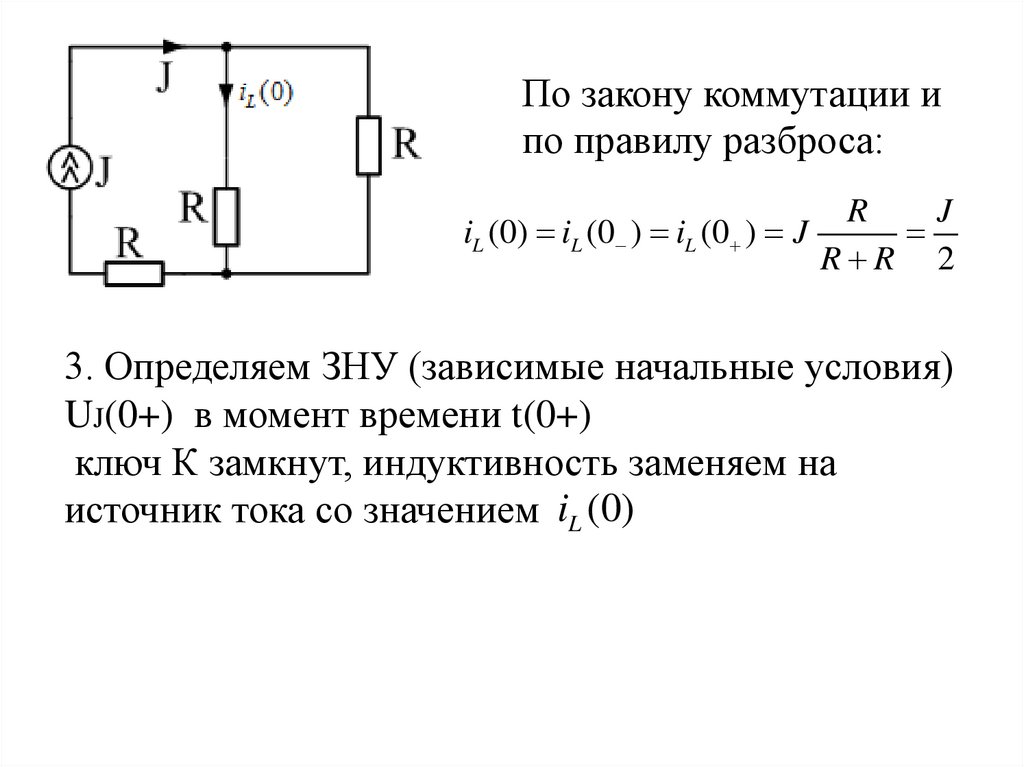
По закону коммутации и
по правилу разброса:
iL (0) iL (0 ) iL (0 ) J
R
J
R R 2
3. Определяем ЗНУ (зависимые начальные условия)
UJ(0+) в момент времени t(0+)
ключ К замкнут, индуктивность заменяем на
источник тока со значением iL (0)

22.

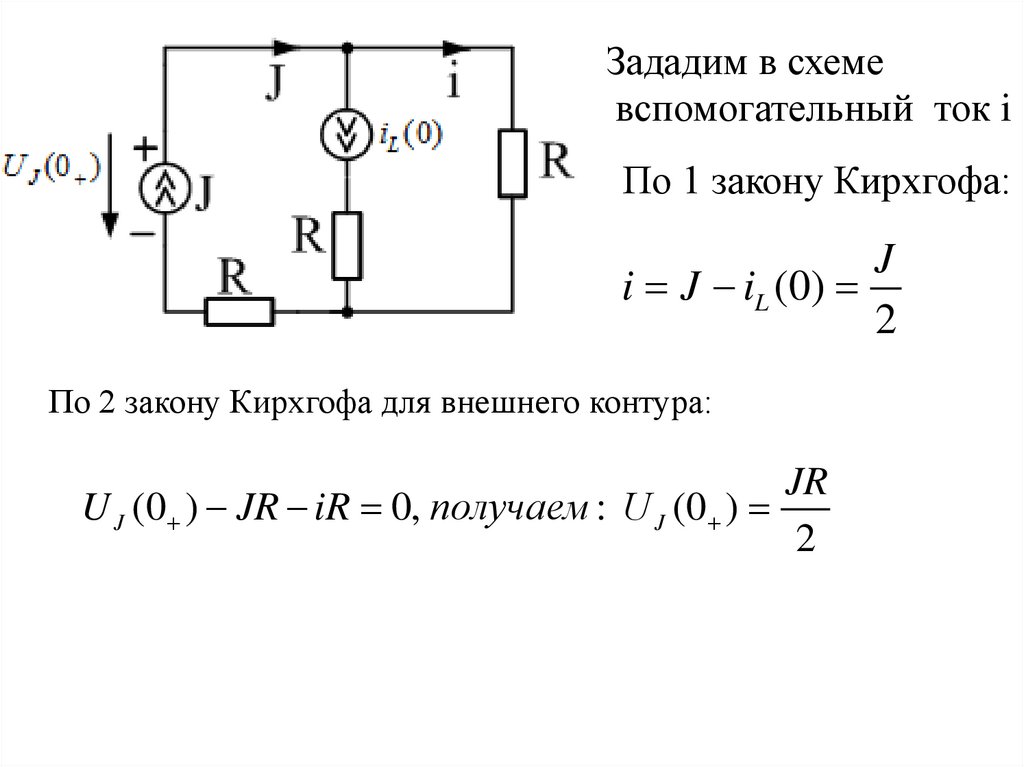
Зададим в схеме
вспомогательный ток i
По 1 закону Кирхгофа:
J
i J iL (0)
2
По 2 закону Кирхгофа для внешнего контура:
JR
U J (0 ) JR iR 0, получаем : U J (0 )
2

23.

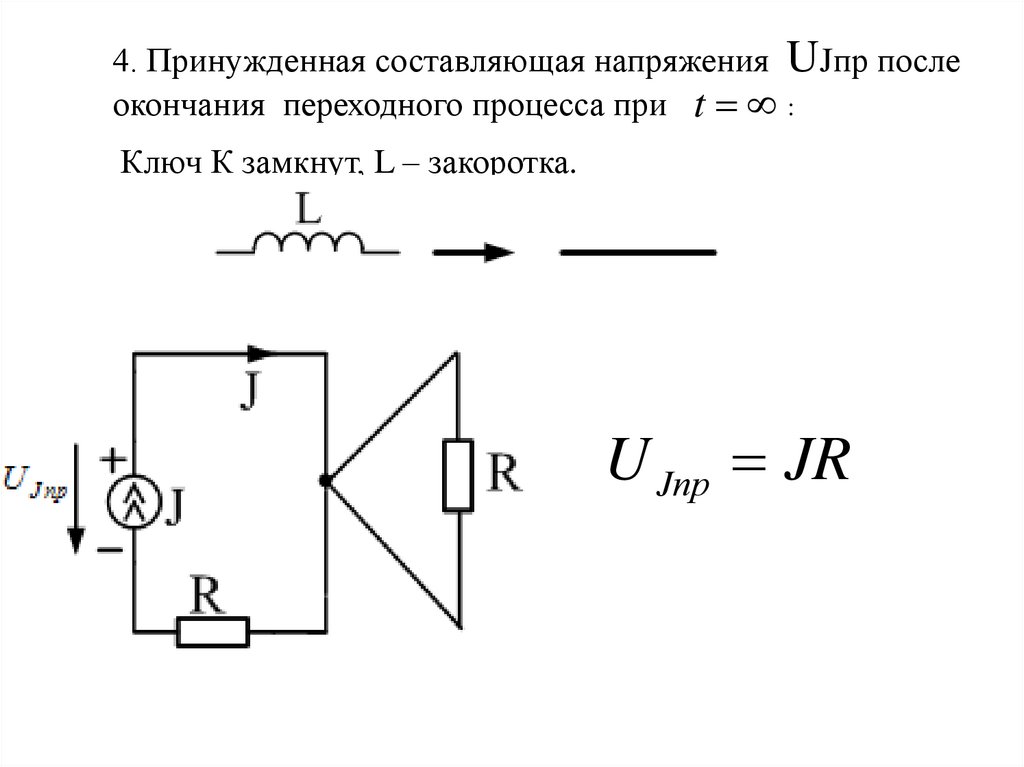
4. Принужденная составляющая напряжения UJпр после
окончания переходного процесса при t :
Ключ К замкнут, L – закоротка.
U Jпр JR

24.

5. Определим корень характеристического уравнения p
по методу сопротивления.
Рисуем вспомогательную схему после коммутации, в
которой размыкаем источник тока J и заменяем
индуктивность L на pL .
Размыкаем полученную схему в любом месте и
определяем сопротивление Z(p) = …... =0
Z ( p) pL R 0
R
40
p
80 1/ c
L
0.5
постоянная времени
1
0.0125 c
p

25.

Уравнение для напряжения переходного процесса
в момент времени t=0+
U J (0 ) U J пр A
потому что e p 0 1
6. Определяем постоянную интегрирования
JR
JR
A U J (0 ) U J пр
JR
2
2
7. Ответ:
t
JR pt
U J (t ) U J пр A e JR
e 80 40e 80t 80 40e A,
2
где 0.0125 с
pt
Длительность переходного процесса t П 5 0.0625 с

26.

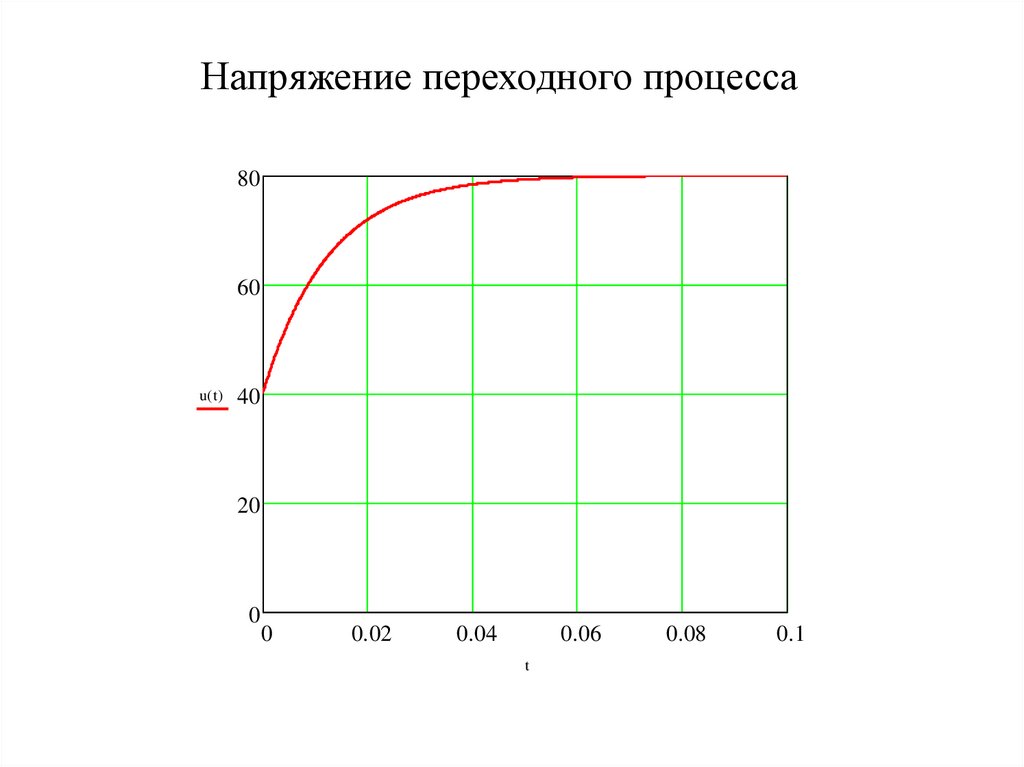
Напряжение переходного процесса
80
60
u( t )
40
20
0
0
0.02
0.04
0.06
t
0.08
0.1

27.

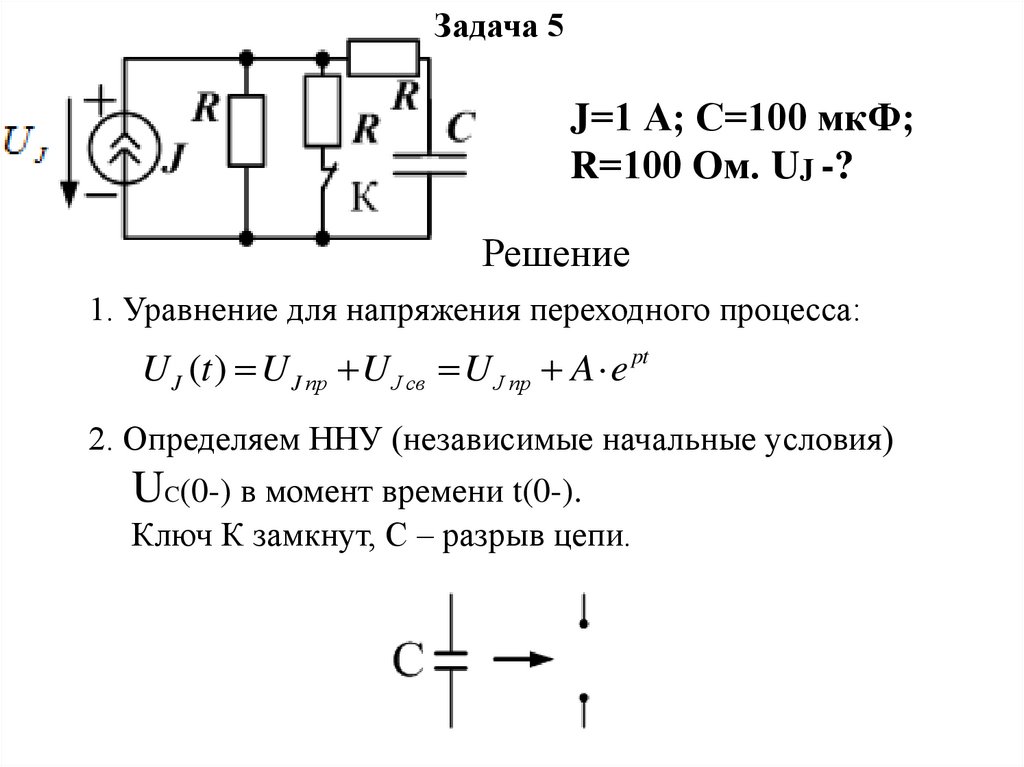
Задача 5
J=1 А; С=100 мкФ;
R=100 Ом. UJ -?
Решение
1. Уравнение для напряжения переходного процесса:
U J (t ) U J пр U J св U J пр A e pt
2. Определяем ННУ (независимые начальные условия)
UC(0-) в момент времени t(0-).
Ключ К замкнут, С – разрыв цепи.

28.

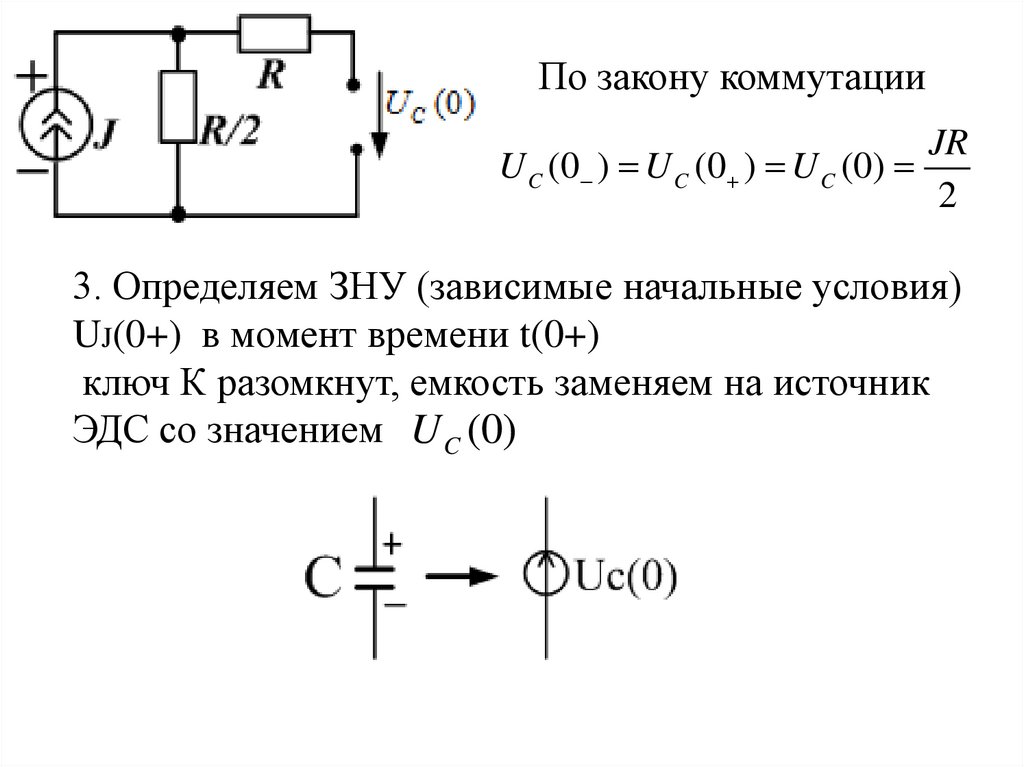
По закону коммутации
JR
U C (0 ) U C (0 ) U C (0)
2
3. Определяем ЗНУ (зависимые начальные условия)
UJ(0+) в момент времени t(0+)
ключ К разомкнут, емкость заменяем на источник
ЭДС со значением U C (0)

29.

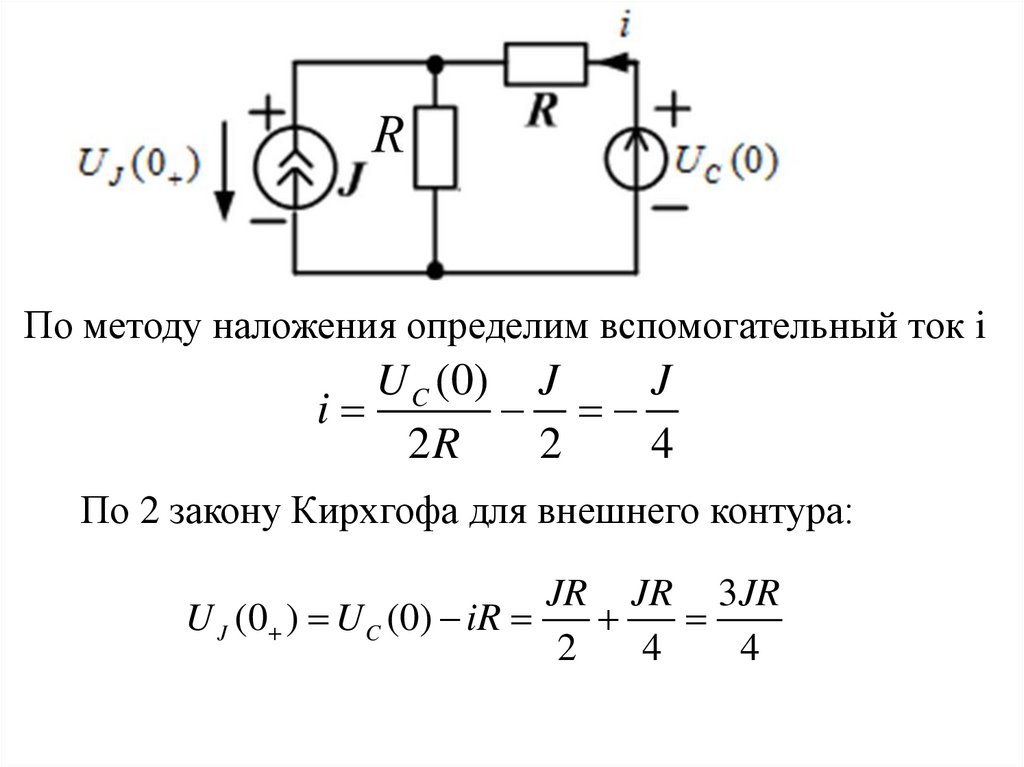
По методу наложения определим вспомогательный ток i
U C (0) J
J
i
2R
2
4
По 2 закону Кирхгофа для внешнего контура:
JR JR 3JR
U J (0 ) U C (0) iR
2
4
4

30.

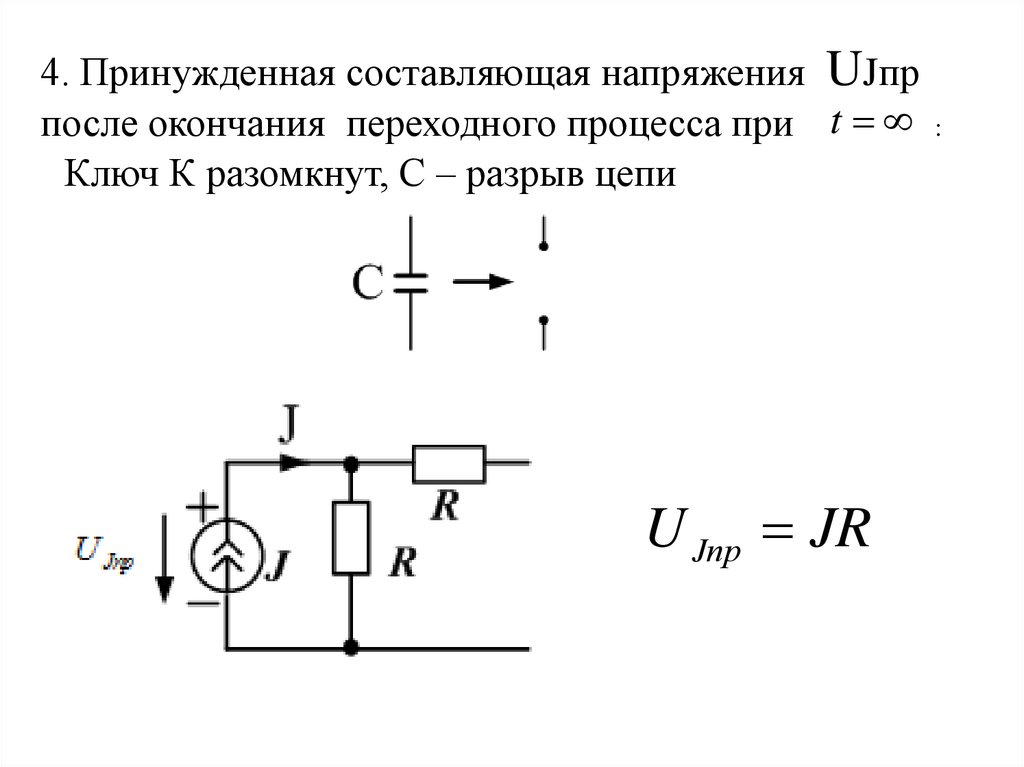
4. Принужденная составляющая напряжения UJпр
после окончания переходного процесса при t :
Ключ К разомкнут, С – разрыв цепи
U Jпр JR

31.

5. Определим корень характеристического уравнения p
по методу сопротивления.
Рисуем вспомогательную схему после коммутации, в
которой размыкаем источник тока J и заменяем
емкость С на 1/рс.
Размыкаем полученную схему в любом месте и
определяем сопротивление Z(p) = …... =0
1
Z ( p) 2 R
0, получаем
pC
1
p
50 1/ c
2 RC
постоянная времени
1
0.02 с
p

32.

Уравнение для напряжения переходного процесса
в момент времени t=0+
U J (0 ) U J пр A
потому что e p 0 1
6. Определяем постоянную интегрирования
3JR
JR
A U J (0 ) U J пр
JR
4
4
7. Ответ:
t
JR pt
U J (t ) U J пр A e JR
e 100 25e 50t 100 25e A,
4
где 0.02 с
pt
Длительность переходного процесса
t П 5 0.1 с

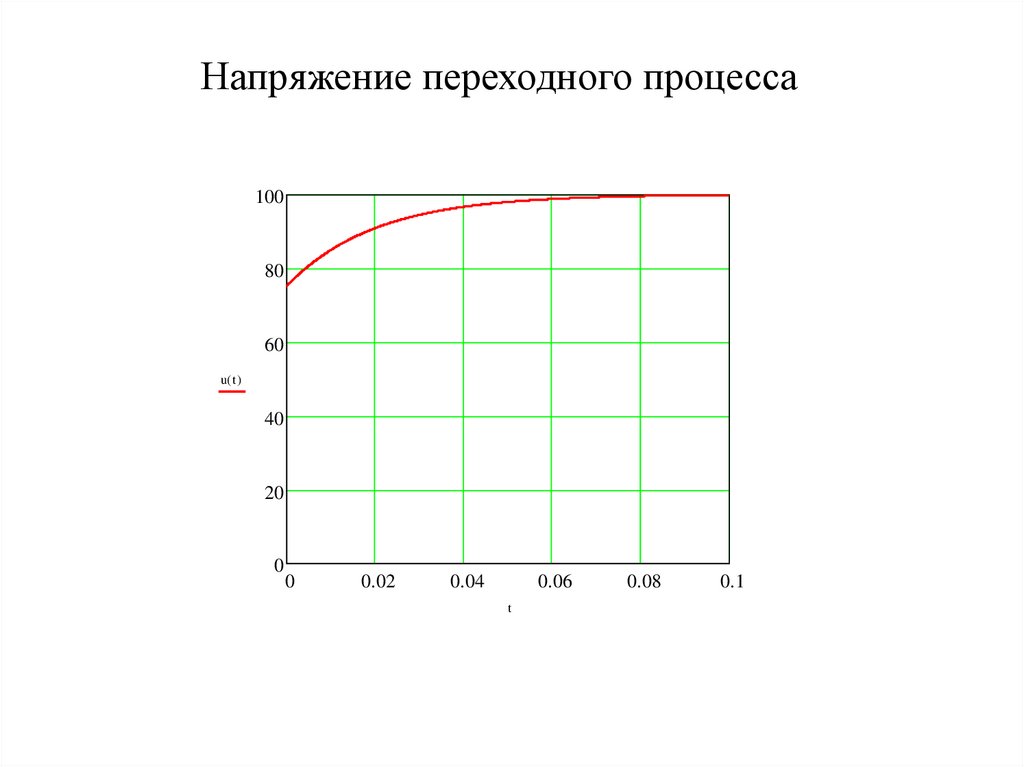
33.

Напряжение переходного процесса
100
80
60
u( t )
40
20
0
0
0.02
0.04
0.06
t
0.08
0.1