динамика вращ. дв.1

1.

3. Динамика вращательного движения твердого тела
Твердое тело – это система материальных точек, расстояния
между которыми не меняются в процессе движения.
При вращательном движении твердого тела все его точки
движутся по окружностям, центры которых лежат на оси вращения.
Рассмотрим основные законы вращательного движения твердого
тела.
Момент инерции
Момент инерции материальной точки относительно оси
вращения равен произведению массы точки на квадрат расстояния от
нее до оси вращения
C
J = mR
2
(1)
Момент инерции точки зависит
только от ее кратчайшего расстояния до оси
вращения.
.
R
r
O
m

2.

Для системы материальных точек момент инерции равен
сумме моментов инерции отдельных точек
J = J i = mi R
2
i
i
i
Если масса распределена непрерывно с плотностью (r ) , то
тело можно разбить на малые объемы ΔVi с массами Δmi = ρi ΔVi.
Эти объемы можно рассматривать как материальные точки.
Суммируя их моменты инерции, получим момент инерции всего тела
J = Δmi R = ρi ΔVi R
2
i
i
2
i
i
В пределе ΔVi 0 сумма переходит в интеграл по объему тела
J = R dm = R ρdV
2
2
(2)
Момент инерции твердого тела зависит от распределения в нем
массы, расстояния и ориентации оси относительно тела.

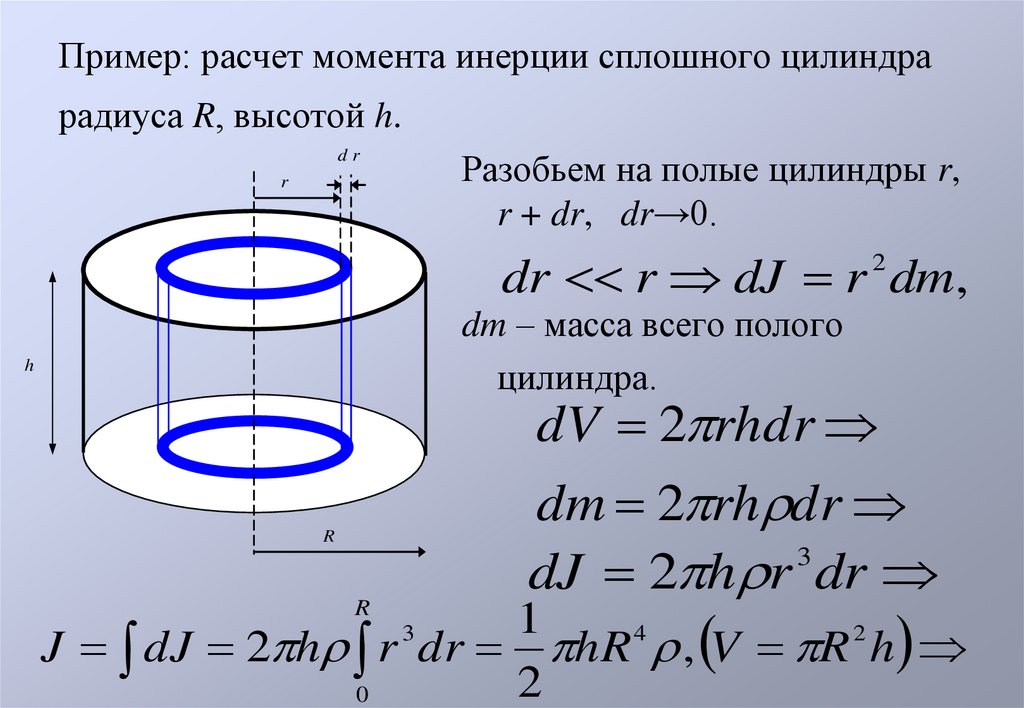
3. Пример: расчет момента инерции сплошного цилиндра радиуса R, высотой h.

Разобьем на полые цилиндры r,
r + dr, dr→0.
dr
r
dr r dJ r dm,
2
dm – масса всего полого
цилиндра.
h
dV 2 rhdr
dm 2 rh dr
3
dJ 2 h r dr
R
1
4
2
J dJ 2 h r dr hR , V R h
2
0
R
3

4.

1
4
2
J dJ 2 h r dr hR , V R h
2
0
R
3
dr
2
r
mR
J
.
2
h
R

5.

Моменты инерции некоторых тел
Шар
I
2
mr 2
5
Однородная
пластинка
1
I
m( a 2 b 2 )
12
Тонкостенная сфера
I
2
mr 2
3
Сплошной цилиндр
1
I mr 2
2
Однородный
стержень
1
I
ml 2
12
Толстостенный
цилиндр
I
1
m( r12 r22 )
2
Диск
I
Диск, когда ось
вращения совпадает
с одним из его
диаметров
1
mr 2
2
Тонкостенный
цилиндр, обруч,
кольцо
I mr
2
I
1
mr 2
4
Произвольное тело
I mi ri 2
5

6.

Теорема Штейнера: момент инерции
относительно произвольной оси равен моменту
инерции относительно параллельной ей оси,
проходящей через центр масс J0, сложенному с
произведением массы тела на квадрат
расстояния между ними а2.
J J 0 ma .
2
2
ml
1 2
l
J J 0 ma
m ml .
12
3
2
2
2

7.

8.

9.

10.

11.

12.

13.

14.

Аналогия между поступательным и
вращательным движениями

15.

Аналогия между поступательным и
вращательным движениями

16.

4.4 Момент силы
Пусть точка О – неподвижная точка в твердом теле, и к
некоторой точке тела А с радиус-вектором r , проведенным из О,
приложена сила F . Тогда векторное произведение
M = [r F ]
(5)
называется моментом силы F относительно неподвижной точки О.
M
Момент силы является псевдовектором,
его
направление
совпадает
с
направлением
поступательного
движения правого винта при его
вращении от r к F . Модуль момента
силы равен
O
r
l
A
F
M = r F sinα = F l
где
l = r sinα -
плечо силы.

17.

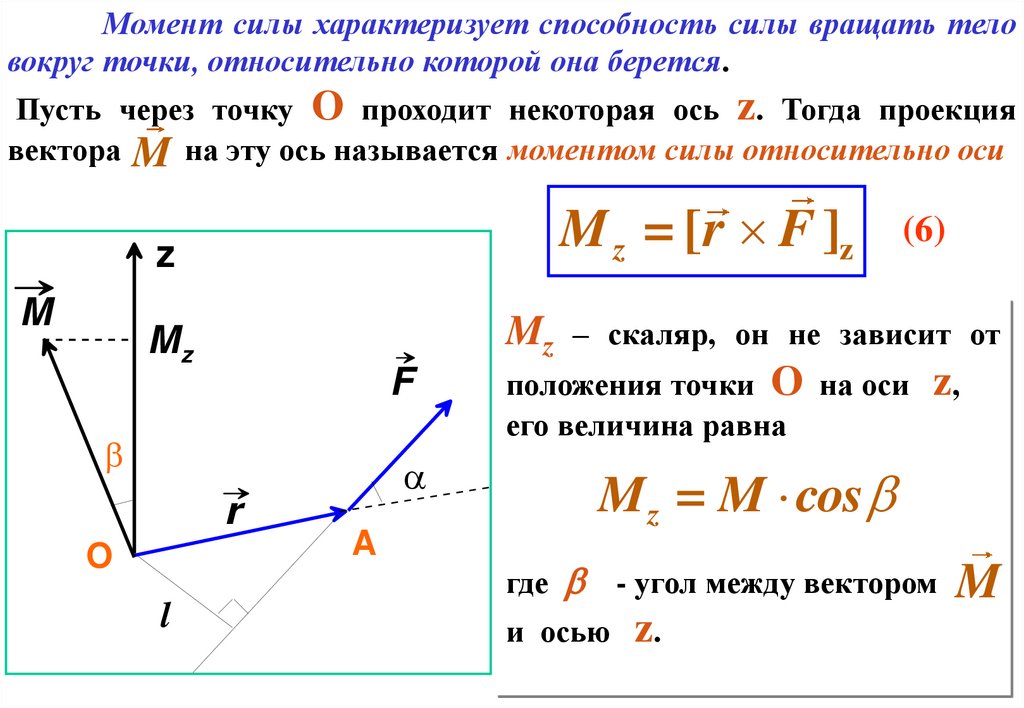
Момент силы характеризует способность силы вращать тело
вокруг точки, относительно которой она берется.
Пусть через точку О проходит некоторая ось z. Тогда проекция
вектора M на эту ось называется моментом силы относительно оси
M z = [r F ]z
z
M
Mz
F
(6)
Mz – скаляр, он не зависит от
положения точки О на оси z,
его величина равна
b
r
O
l
A
M z = M cosb
где b
- угол между вектором M
и осью
z.

18.

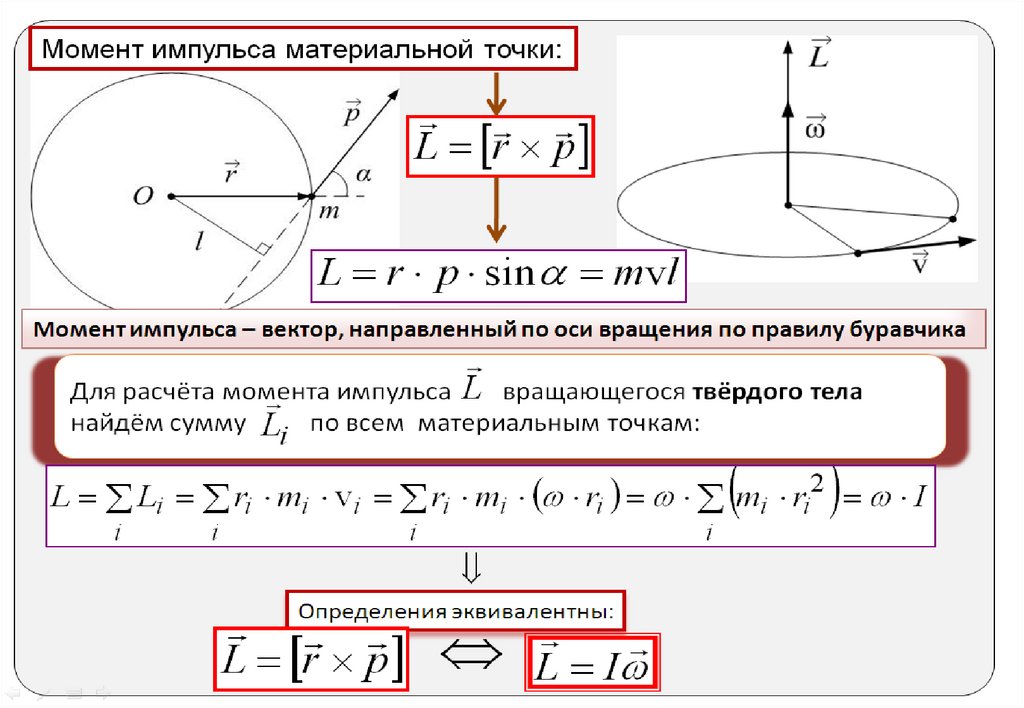
4.6 Момент импульса
Моментом импульса материальной точки А относительно
неподвижной точки О называется псевдовектор, равный
L = [r p] [r m ]
L
z
где - радиус-вектор точки А .
Направление псевдовектора L
совпадает с направлением
поступательного движения правого
винта при его вращении от r к p .
Модуль момента импульса равен
r
b
R
O
b
l
(9)
P
r
A
L = r p sinα = p l
где l = r sinα - плечо импульса

19.

Моментом
импульса
материальной
точки
относительно неподвижной оси z называется величина,
равная проекции вектора момента импульса на эту ось
Lz = [r p]z L cosβ
(10)
Для твердого тела момент импульса относительно
неподвижной точки равен сумме моментов элементарных объемов,
выступающих в роли материальных точек
L = Li = [ri pi ]
i
i

20.

Поэтому
момент
неподвижной оси
тела
z
импульса
твердого
тела
относительно
равен сумме моментов элементарных объемов
Lz = Liz = [ri pi ]z Li cosb i
i
i
i
Пусть тело вращается вокруг неподвижной оси z с угловой
скоростью
. Каждая точка тела движется по окружности
постоянного радиуса Ri со скоростью i , перпендикулярной этому
радиусу и радиус-вектору точки ri , поэтому угол между
i и ri прямой = /2 .
i

21.

Поскольку плечо силы
i - ой точки равно Ri = ri cos b i
, то
[ri pi ]z ri pi sin i cosbi Ri pi
Lz Ri pi Ri mi i
i
i
При вращательном движении все точки тела движутся с одной
угловой скоростью
, величина которой связана с линейной
скоростью υi = ω Ri , поэтому
Lz mi Ri = J z
2
Lz J z
i
(11)
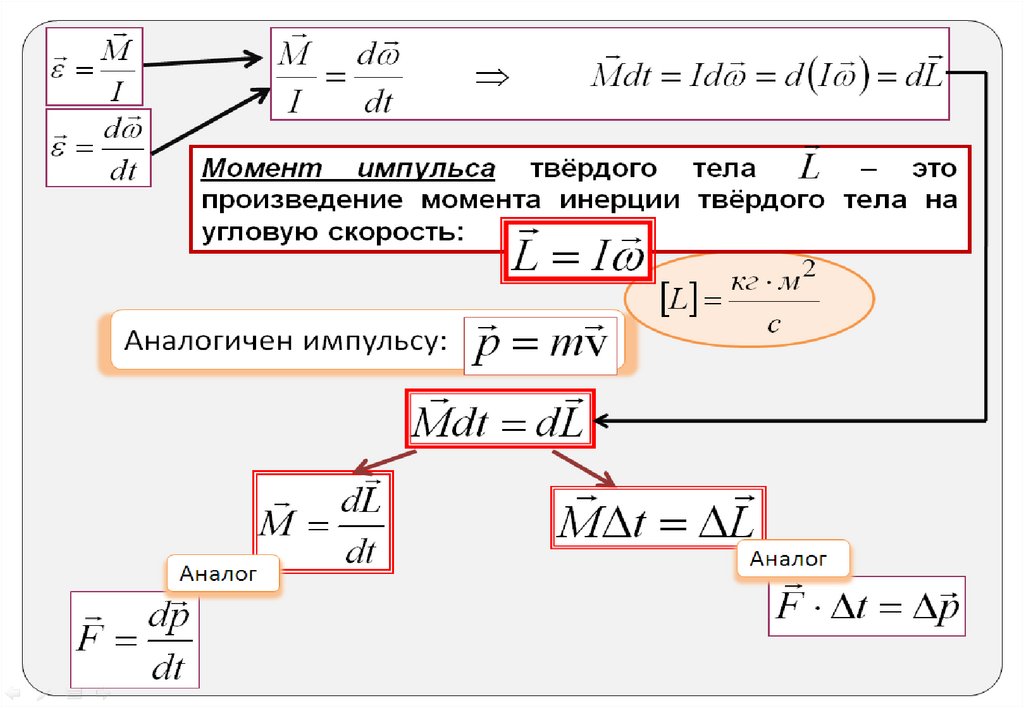
Момент импульса твердого тела относительно оси
равен произведению моменту инерции тела относительно
той же оси на угловую скорость.

22.

Возьмем производную по времени от последнего равенства
dLz d ( J z )
d
=
= Jz
Jz
dt
dt
dt
Но согласно (5.4.4)
относительно оси z , поэтому
Mz = J z -
есть момент силы
dLz
Mz =
dt
(12)
Производная по времени от момента импульса
твердого тела относительно некоторой оси равна моменту
внешних сил относительно той же оси.
Уравнение (12) есть другая форма уравнения динамики
вращательного движения твердого тела. Она устанавливает связь
между проекциями векторов M и L на ось вращения.

23.

Теперь найдем связь между векторами M и L .
Для этого возьмем производную по времени от формулы (5.5.1) для
вектора L
dL
dL
dr
dp
dt
=
i
i
dt
= [
i
i
dt
pi ] [ri
i
i
dt
]
dri
pi ] = [ i pi ] = mi [ i i ] = 0
Но [
dt
dL
dpi
= [ri
] [ri Fi ] M i M
поэтому
dt
dt
i
i
i
Уравнение динамики вращательного
движения твердого тела в векторном виде
dL
=M
dt
(5.5.5)
Производная по времени от момента импульса
твердого тела относительно неподвижной точки равна
моменту внешних сил относительно той же точки.