Похожие презентации:
Презентация_по_геометрии_На_тему_Соотношения_между_сторонами_и_углами
1.
2.
AB
C
3.
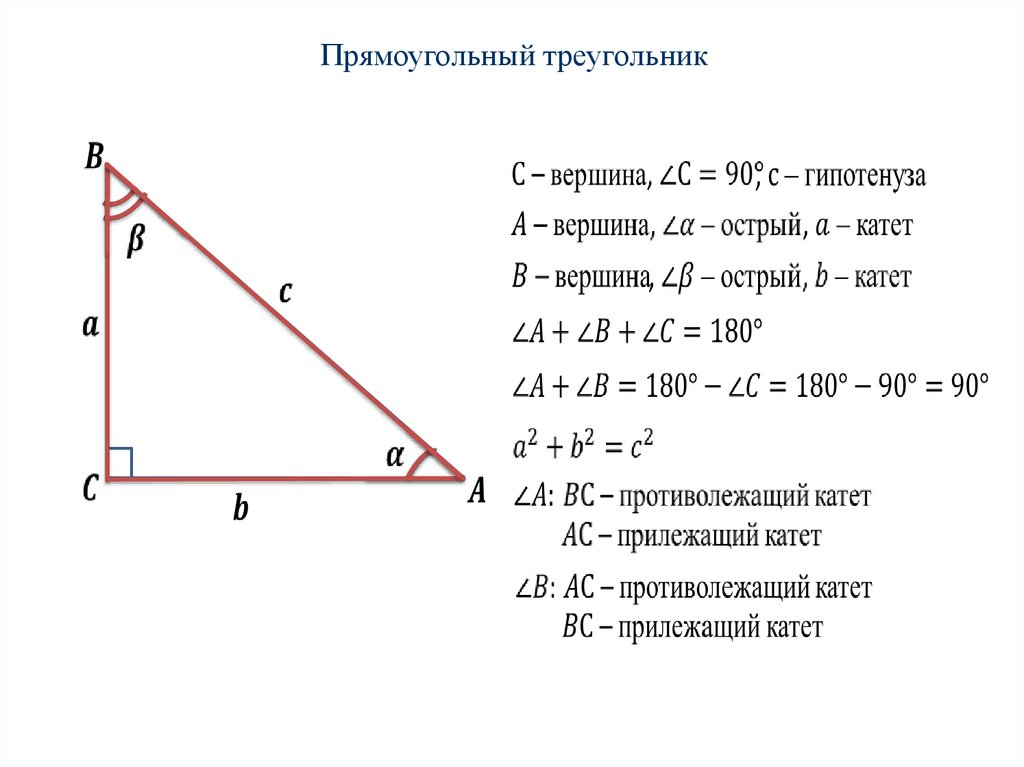
Прямоугольный треугольник4.
Определение: синусом острого угла прямоугольного треугольниканазывается отношение противолежащего катета к гипотенузе.
Определение: косинусом острого угла прямоугольного треугольника
называется отношение прилежащего катета к гипотенузе.
Определение: тангенсом острого угла прямоугольного треугольника
называется отношение противолежащего катета к прилежащему.
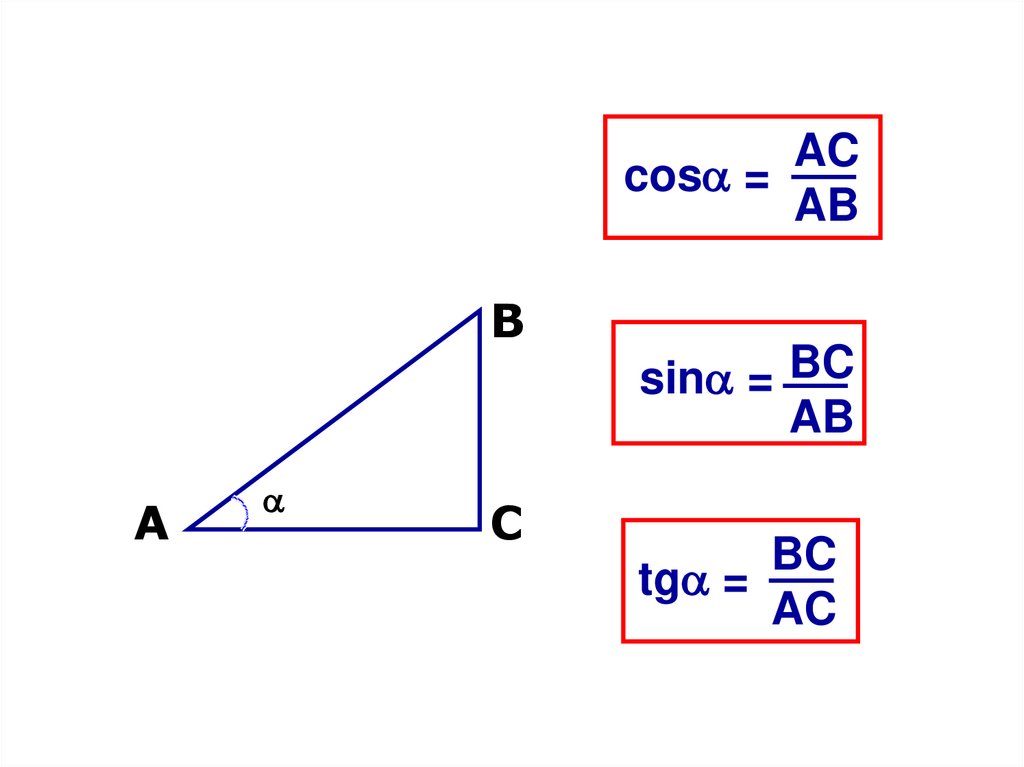
5.
ACcos =
AB
B
A
C
sin = BC
AB
BC
tg =
AC
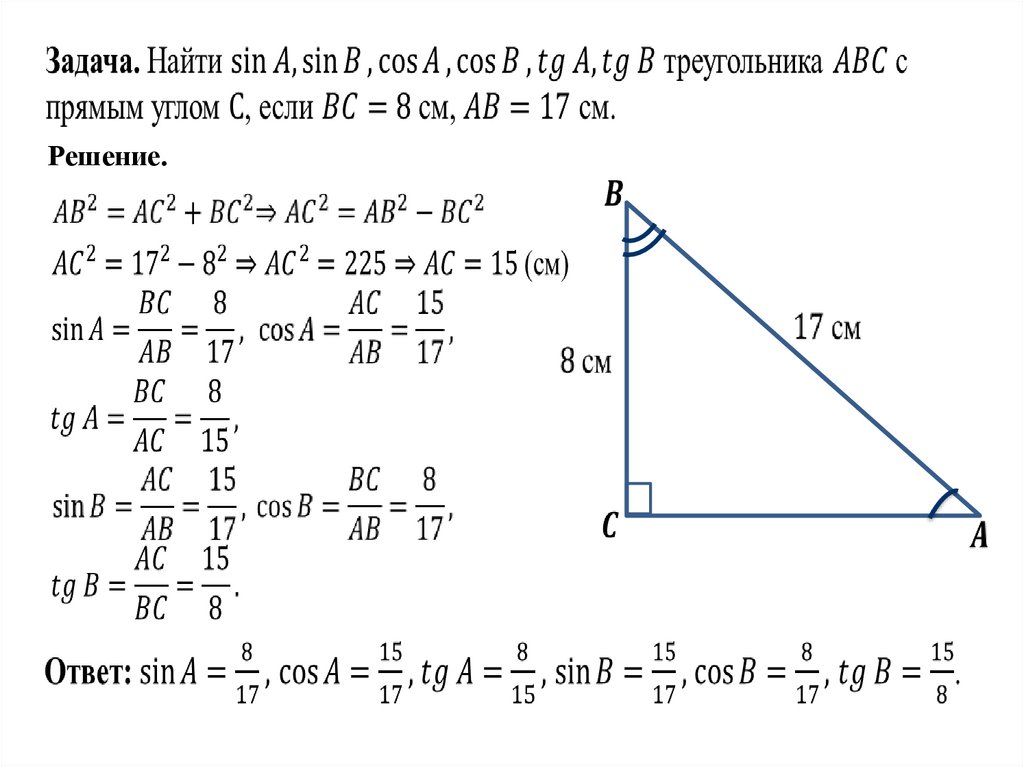
6.
Решение.7.
8.
− основное тригонометрическоетождество
− тригонометрические функции
Тригонометрия − происходит от греческих слов
τρίγωνον (треугольники) и μέτρεο (измеряю)
Тригонометрия − раздел математики, в котором
изучают тригонометрические функции и их
использование в геометрии.
9.
ОСНОВНОЕТРИГОНОМЕТРИЧЕСКОЕ
ТОЖДЕСТВО
sin cos 1
2
2
10.
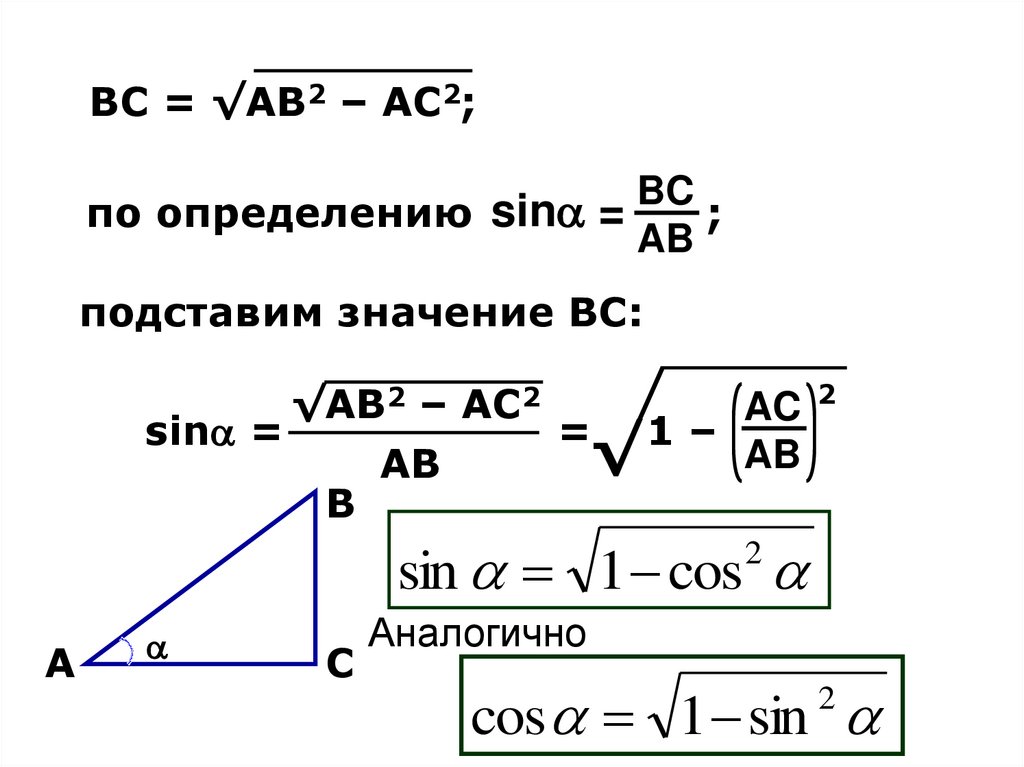
ВС = √АВ2 – АС2;BC
sin
=
по определению
;
AB
подставим значение ВС:
√АВ2 – АС2
AC 2
sin =
= 1–
AB
√
AВ
B
sin 1 cos
2
A
C
Аналогично
cos 1 sin
2
11.
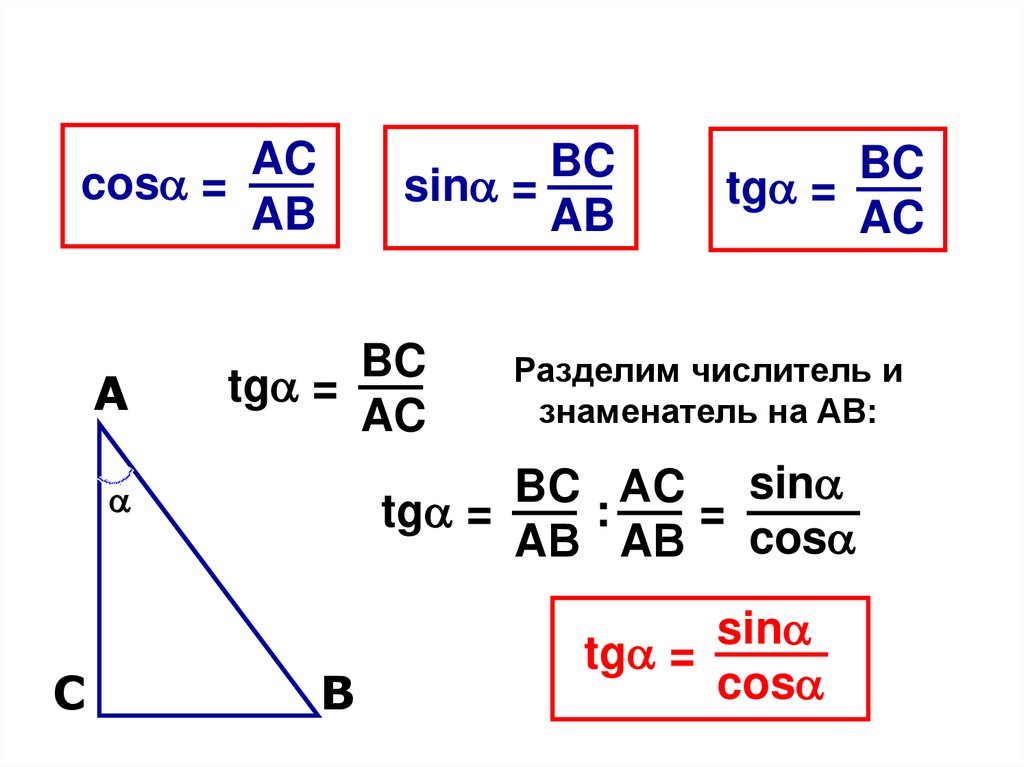
ACcos =
AB
A
BC
sin =
AB
BC
tg =
AC
Разделим числитель и
знаменатель на АВ:
BC АC sin
:
=
tg =
AВ AВ cos
C
BC
tg =
AC
B
sin
tg =
cos
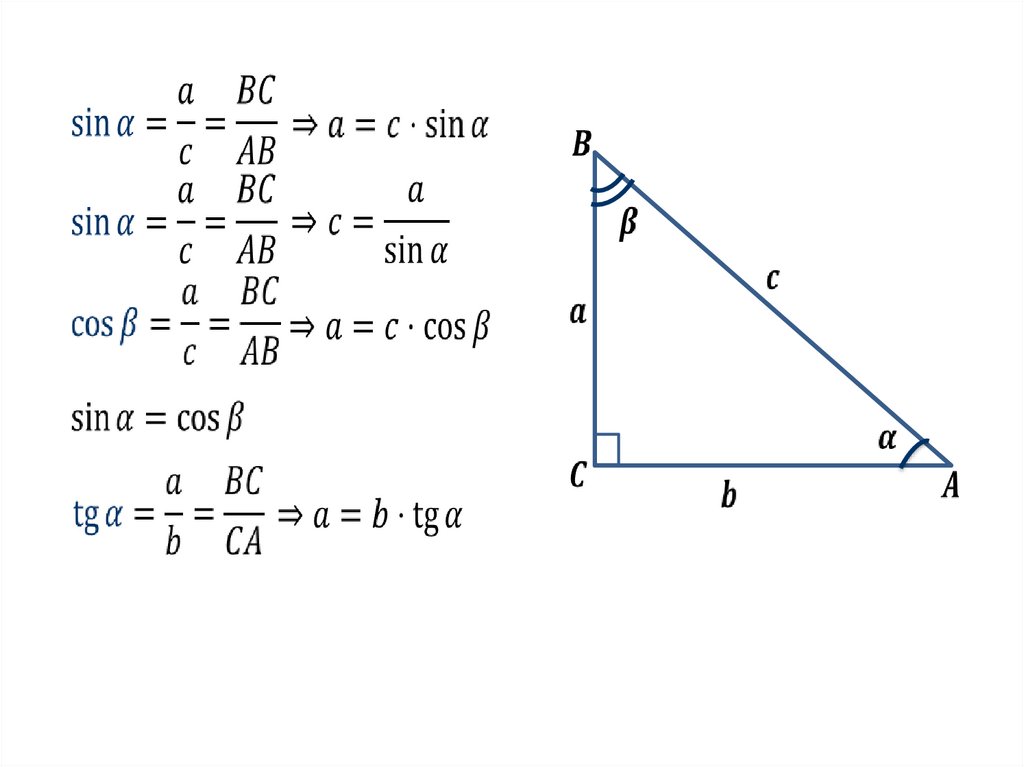
12.
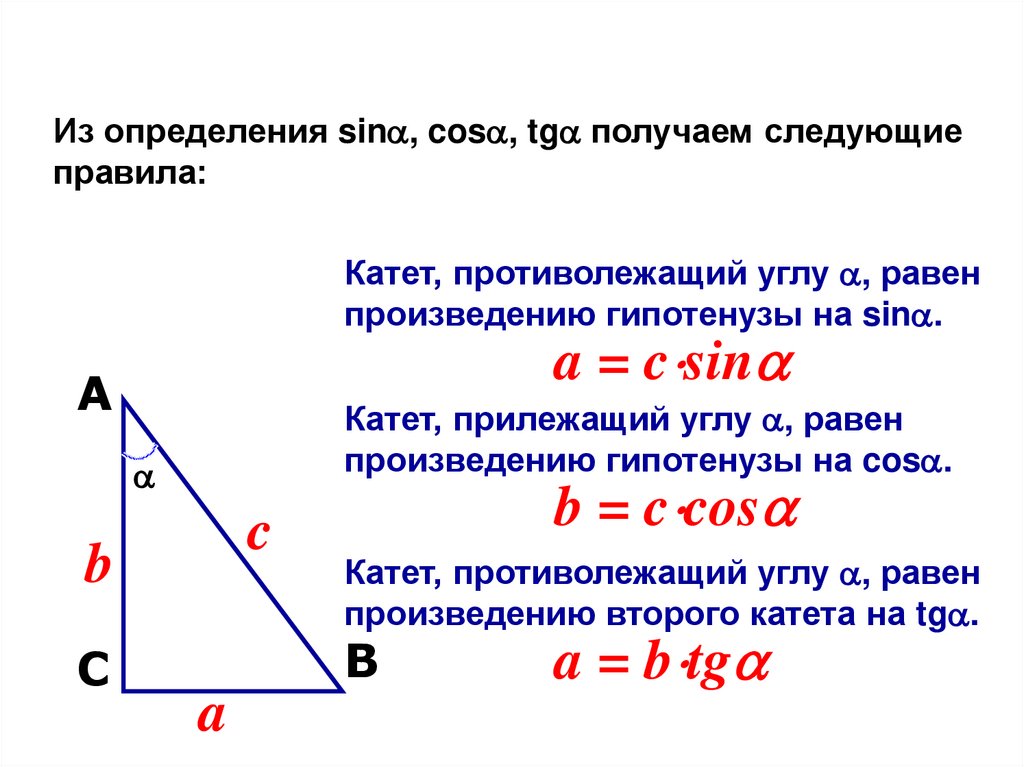
Из определения sin , cos , tg получаем следующиеправила:
Катет, противолежащий углу , равен
произведению гипотенузы на sin .
a = c sin
A
Катет, прилежащий углу , равен
произведению гипотенузы на cos .
c
b
C
b = c cos
Катет, противолежащий углу , равен
произведению второго катета на tg .
B
a
a = b tg
13.
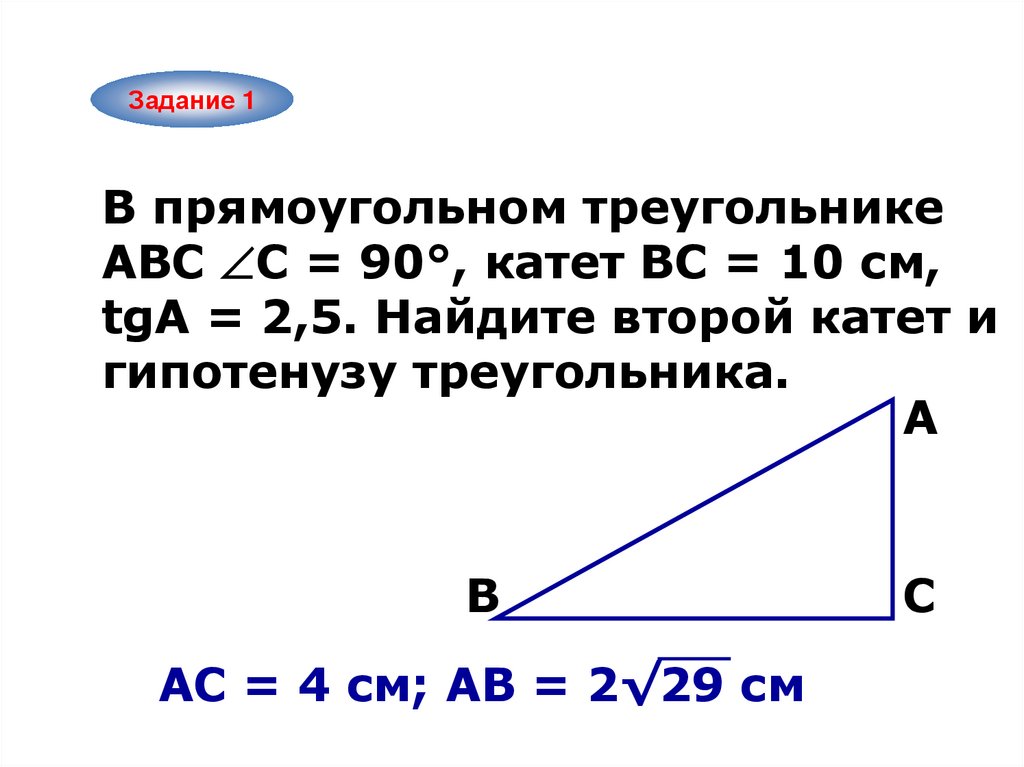
Задание 1В прямоугольном треугольнике
ABC С = 90°, катет ВС = 10 см,
tgА = 2,5. Найдите второй катет и
гипотенузу треугольника.
A
B
АC = 4 см; АВ = 2√29 см
C
14.
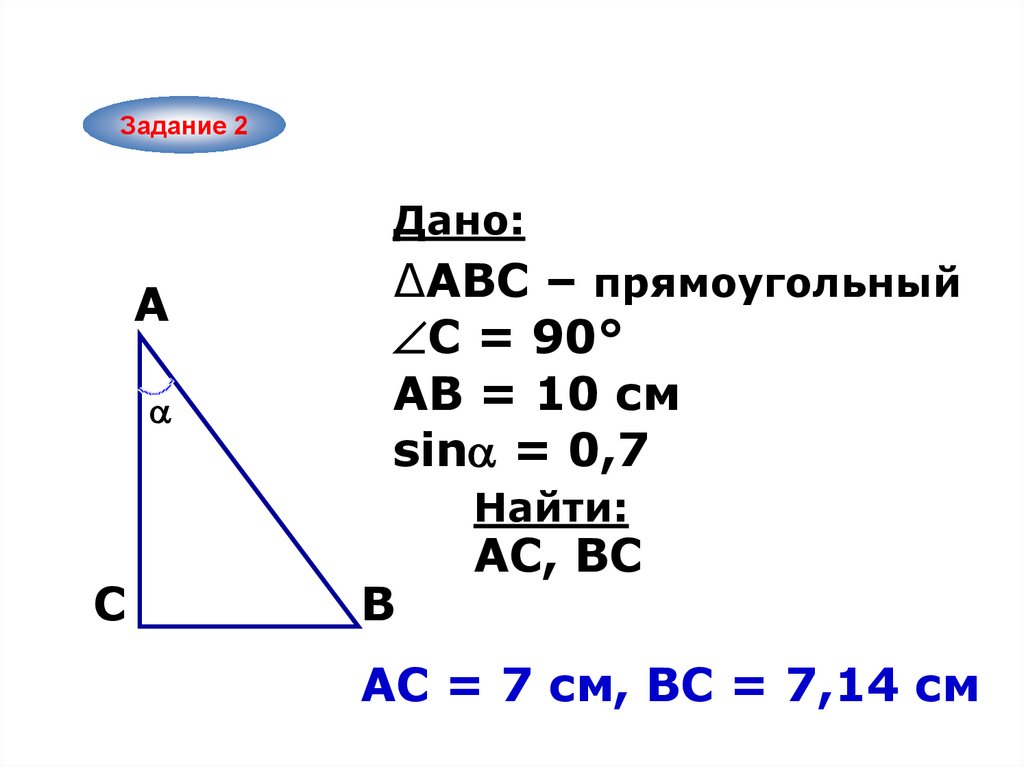
Задание 2Дано:
A
∆ABC – прямоугольный
С = 90°
АВ = 10 см
sin = 0,7
Найти:
C
B
AС, ВС
АС = 7 см, ВС = 7,14 см
15.
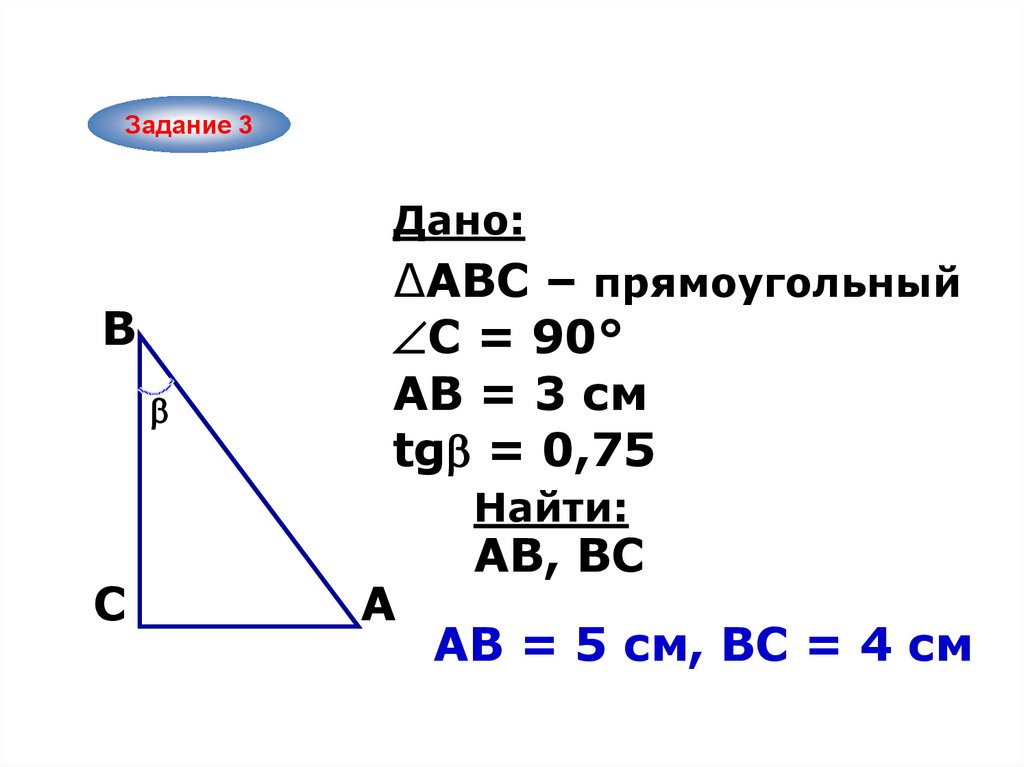
Задание 3Дано:
B
∆ABC – прямоугольный
С = 90°
АВ = 3 см
tg = 0,75
Найти:
C
A
AB, ВС
АB = 5 см, ВС = 4 см
16.
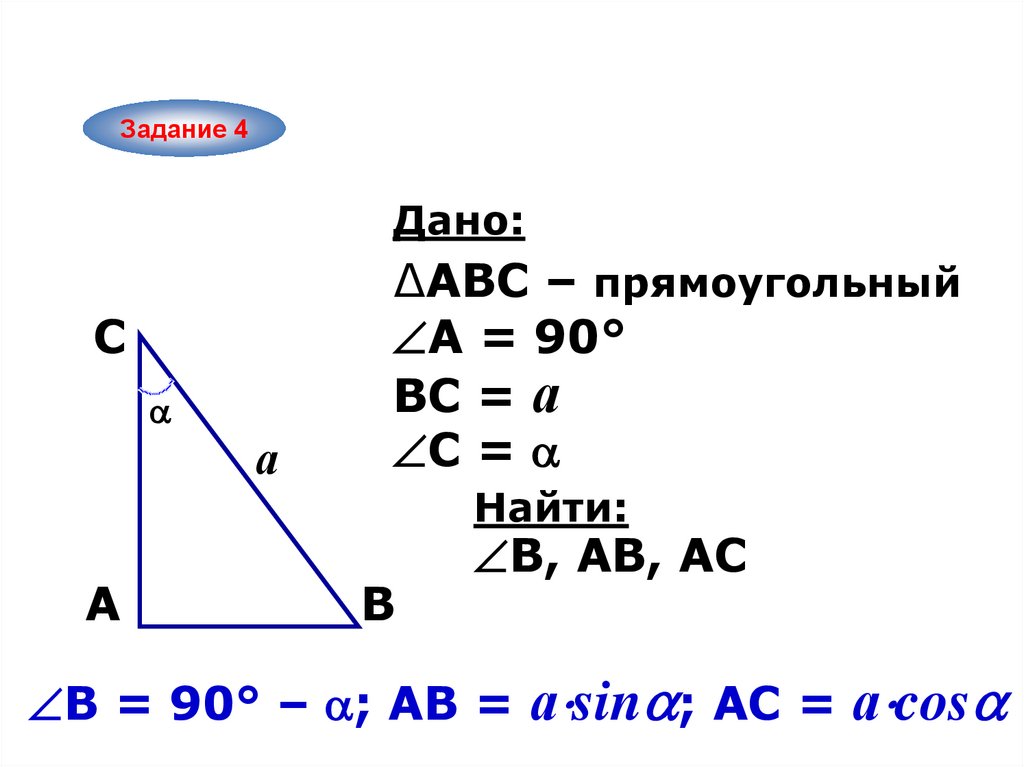
Задание 4Дано:
C
а
A
∆ABC – прямоугольный
A = 90°
ВC = а
С =
Найти:
B
В, AB, АC
В = 90° – ; АВ = а sin ; AС = а cos
17.
Решение.18.
В классе решить:Стр. 159 № 591 (а,б),
№ 592(а),№ 593(а, б)
19.
Дома:Стр.159
№ 591 (в),
№ 592(б),
№ 593(в)



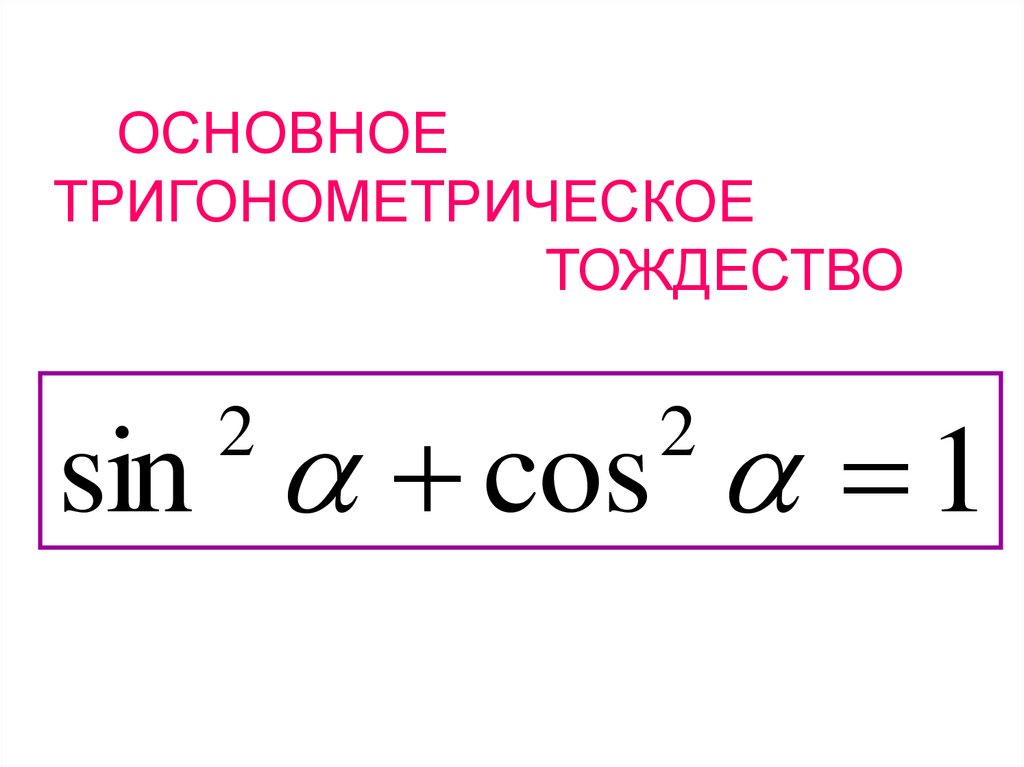
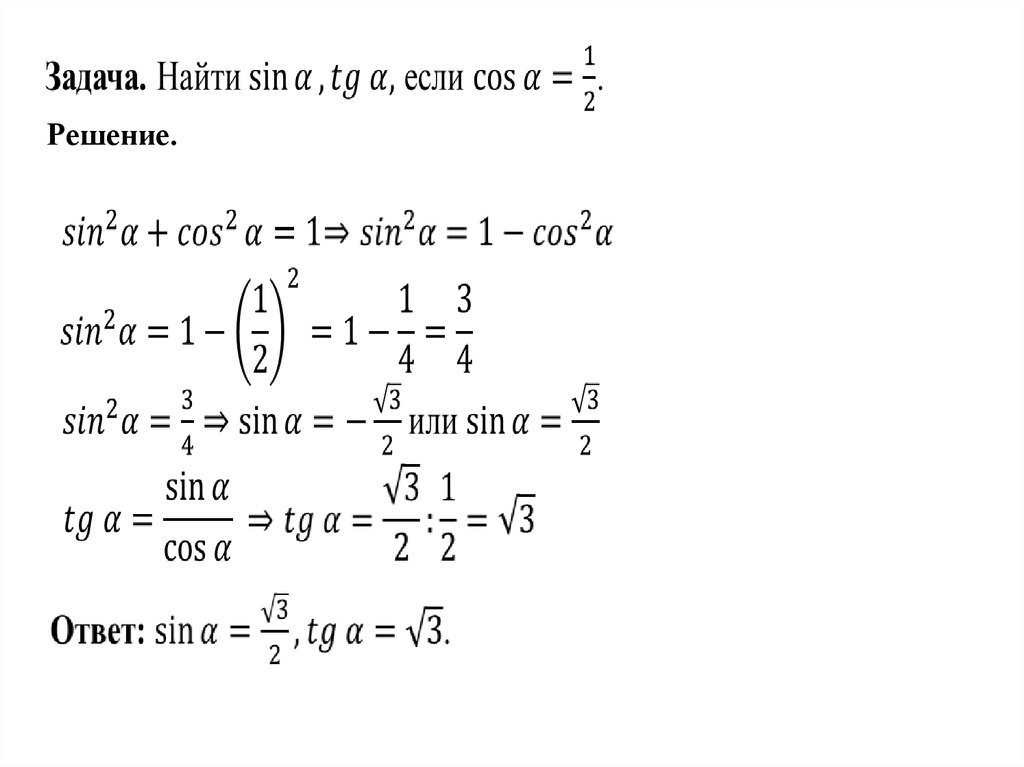


 Математика
Математика








