Динамика_6

1. Лекция 6

Работа силы и мощность. Кинетическая энергия.
Теорема об изменении кинетической энергии.

2.

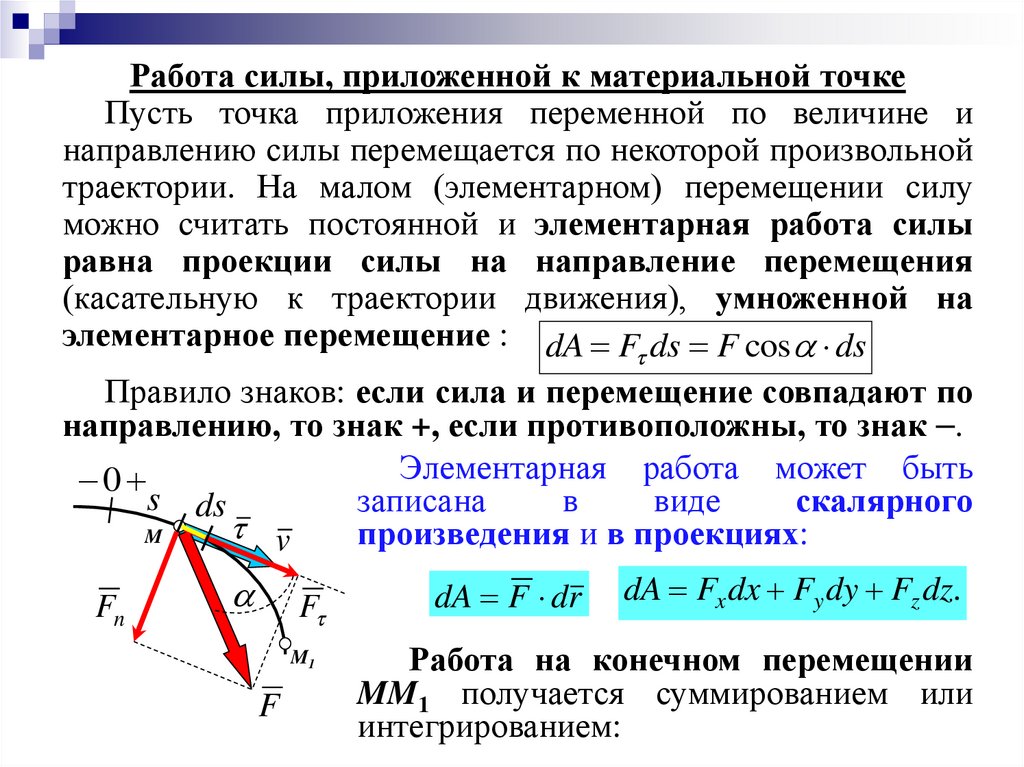
Работа силы, приложенной к материальной точке
Пусть точка приложения переменной по величине и
направлению силы перемещается по некоторой произвольной
траектории. На малом (элементарном) перемещении силу
можно считать постоянной и элементарная работа силы
равна проекции силы на направление перемещения
(касательную к траектории движения), умноженной на
элементарное перемещение : dA F ds F cos ds
Правило знаков: если сила и перемещение совпадают по
направлению, то знак +, если противоположны, то знак .
Элементарная работа может быть
0
s ds
записана
в
виде
скалярного
v
M
произведения и в проекциях:
F
dA F dr dA Fx dx Fy dy Fz dz.
Fn
M1
F
Работа на конечном перемещении
MM1 получается суммированием или
интегрированием:

3.

M1
0
M1
A F ds A F dr
s ds
M
M
v
Fn
(F dx F dy F dz)
x
y
z
M
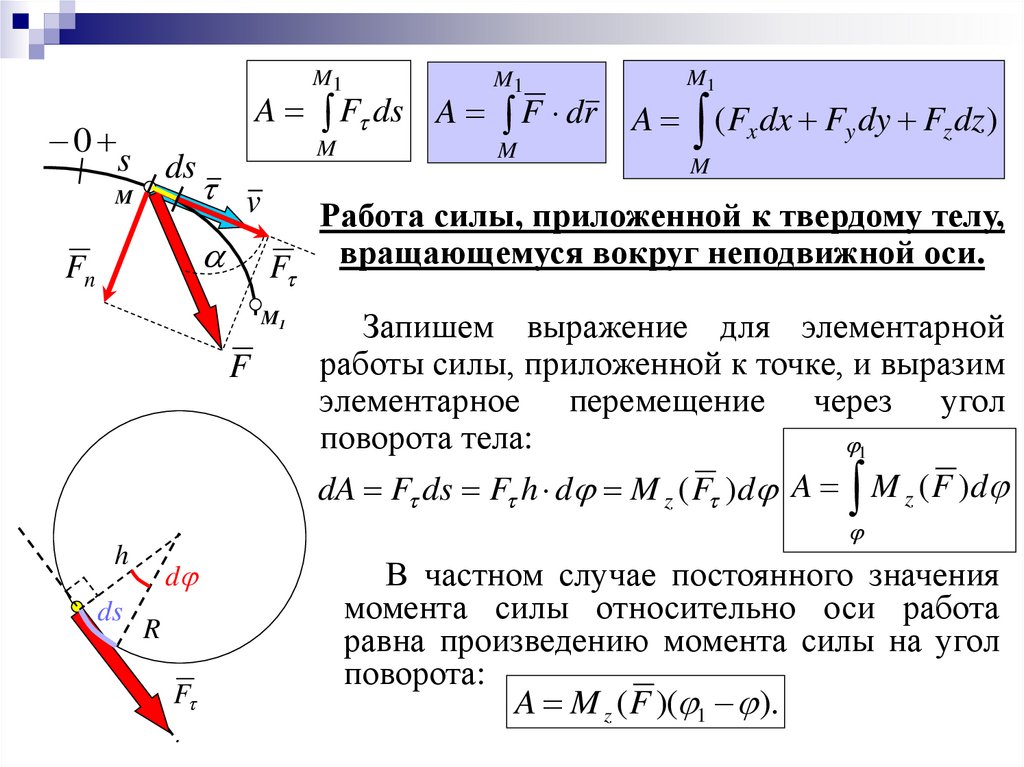
Запишем выражение для элементарной
работы силы, приложенной к точке, и выразим
элементарное перемещение через угол
поворота тела:
1
dA F ds F h d M z ( F )d A M z ( F )d
h
ds
A
Работа силы, приложенной к твердому телу,
F вращающемуся вокруг неподвижной оси.
M1
F
M
M1
d
R
F
В частном случае постоянного значения
момента силы относительно оси работа
равна произведению момента силы на угол
поворота:
A M z ( F )( 1 ).

4.

0
s ds
M
Fn
v
F
M1
F
Частные случаи:
1. Сила постоянная по величине (F = const)
и направлению ( = const):
M1
M1
M
M
A F cos ds F cos ds Fs cos .
2. Сила постоянная по величине
и параллельна перемещению ( =0):
A Fs.
3. Сила перпендикулярна перемещению:
A 0
Единицей измерения работы в системе СИ - 1 джоуль
(1 Дж = 1H м = 1 кг м2 /с2).
Можно доказать следующие теоремы и утверждения:
Работа равнодействующей на некотором перемещении
равна алгебраической сумме работ составляющих сил на том
же перемещении:
A Ai

5.

Работа силы, постоянной по величине и направлению,
на составном перемещении равна алгебраической сумме
работ этой силы на каждом из составляющих
перемещений:
A Asi
Работа внутренних сил неизменяемой системы
i
A
0
равна нулю:
Работа силы тяжести не зависит от вида
траектории и равна произведению силы
A G(h1 h)
тяжести на разность высот:
Работа линейной силы упругости (реакции
2
Δl
пружины) при перемещении из состояния
A c
.
равновесия l:
2
Мощность – величина, характеризуемая количеством
работы, произведенной в единицу времени:
dA F ds
N
F v
Единицей
измерения
dt
dt
мощности
в системе
СИ
M z d
N
M z M
является ватт (1 Вт = 1Дж/с).
dt
В технике - 1 л.с. = 736 Вт.

6.

Кинетическая энергия – характеризует способность
механического движения превращаться в эквивалентное
количество другого движения:
Кинетическая энергия
Кинетическая энергия
материальной точки:
системы материальных
точек:
2
2
mv
m
v
M
T
V
T k k
2
2
Кинетическая энергия - скалярная величина.
Единица измерения кинетической энергии в системе СИ - 1 Дж.
Кинетическая энергия твердого тела
MvC2
Кинетическая энергия твердого тела при
T
2
поступательном движении:
I z z2
Кинетическая энергия твердого тела при
T
вращательном движении:
2
Кинетическая энергия твердого тела при
MvC2 I zC z2
T
плоском движении:
2
2

7.

Теорема об изменении кинетической энергии
материальной точки
Изменение кинетической энергии точки равно работе сил,
действующих на точку на том же перемещении:
В дифференциальной
форме:
mv 2
d(
2
)
dAk
M1
mv2 mv02
2
2
A( MM )
M
v
1
Теорема об изменении кинетической энергии системы
Изменение кинетической энергии системы равно работе
сил, действующих на систему на соответствующих
перемещениях точек системы.
mk vk2 mvk20
i
e
A
A
k
k.
Для произвольной точки системы:
2 2
2
2
mk vk
mvk 0
i
e
Для системы:
A
A
2 2 k k.
Окончательно получаем:
Для неизменяемой
i
e
T T0
Ak
Ak . системы:
T T0 Ake ; Aki 0