3сем_Лк 4_Лин ДУ с перемен коэф

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет императрицы Екатерины II
Кафедра высшей математики
Лекция 4.
Линейные однородные ДУ 2-го порядка
с переменными коэффициентами
22.12.2025
г. Санкт-Петербург
2025
1|12

2.

Линейное однородное ДУ 2-го порядка
y p1 ( x ) y p 2 ( x ) y 0
(1
)
ДУ (1) имеет единственное решение,
удовлетворяющее при любом x0 (a, b)
в интервале (а, b)
заданным начальным условиям:
y ( x0 ) y0 , y ( x0 ) y0 .
Особых решений ДУ (1) не имеет
p1 ( x), p 2 ( x) непрерывны
Теорема. Если у1(х) и у2(х) – решения ЛОДУ (1), то функции у1(х) + у2(х) и
Су1(х), где С =const, также его решения.
Доказательство.
y1 p1 ( x) y1 p2 ( x) y1 0,
у (х) и у (х) – решения (1)
y y p ( x) y y p ( x) y y 0.
1
2
+
1
y2 p1 ( x) y2 p2 ( x) y2 0
2|12
2
1
1
2
2
у1(х)+у2(х) – решение (1)
1
2

3.

Следствие.
Если у1(х), у2(х),…, уm(х) – решения ЛОДУ (1), а С1, С2,…, Сm – произвольные постоянные,
то функция
y( x) C1 y1 ( x) C2 y2 ( x) Cm ym ( x) также является решением ЛОДУ (1)
Функции у1(х), у2(х),…, уm(х) в интервале (а, b) называются
линейно зависимыми
линейно независимыми
если существуют постоянные
С1, С2,…, Сm , одновременно
0,
что х (а, b) выполнено
С1 у1(х) + С2 у2(х)+…+ Сm уm(х) =0 (*)
равенство:
если равенство (*) выполняется
х (а, b) только при
C1 = C2 =...= Cт= 0 .
Одна из функций может быть выражена
через остальные.
Пример 1. Функции 1, sin2х, cos2х заданы в интервале (– ,
sin2х+ cos2х =1.
). Они линейно зависимые?
Равенство C1 + C2 sin2 х + C3 cos2 х = 0 выполняется
C1 =1, C2 = C3=–1:
3|12
х
(– ,
), если

4.

:
Пример 2. Будут ли функции 1, х, х2 – линейно зависимыми в интервале (– ,
)?
Существуют
ли C , C , C , чтобы х (– , ) выполнялось равенство C + C х + C х2 = 0?
1
2
3
1
2
3
Равенство выполняется только при C1 =C2 = C3=0
Функции линейно независимы.
y1 ( x )
y2 ( x )
ym ( x )
Определител
y1 ( x )
y2 ( x )
ym ( x )
ь Вронского:
w( x )
Пусть функции
у1(х), у2(х),…, уm(х) имеют в
интервале (а, b) непрерывные
производные до порядка
т – 1 включительно.
y1( m 1) ( x ) y2( m 1) ( x ) ym( m 1) ( x )
его значение – вронскиан.
Теорема. Если функции у1(х), у2(х) линейно зависимы в интервале (а, b),
то определитель Вронского w(x)=0
Доказательство.
Одна
Функции у1(х), у2(х)
выражается
линейно зависимы
через другую
в интервале (а, b),
y ( x ) y ( x )
2
х
(а, b).
y1 y 2
w( x)
y1 y 2
y1 y1
y1 y1 y1 y1
y1 y1
х
1
4|12
0
(а, b)

5.

Следствие. Если для функций у1(х) и у2(х) вронскиан w(x) 0
х
то в этом интервале функции линейно независимые.
(а, b),
Теорема (Остроградского–Лиувилля). Если определитель Вронского составленный
для решений у1(х) и у2(х) ЛОДУ (1) не равен нулю при каком-нибудь значении х0 (а, b),
где коэффициенты уравнения непрерывны, то он в этом интервале не обращается в
нуль.
Доказательство.
у1(х)
y2 + p1 ( x) y2 + p2 ( x) y2 0
y1 y 2
w( x)
y1 y 2 y1 y 2
Функции у1(х), у2(х)
у2(х)
y1 y 2
y
+
p
(
x
)
y
+
p
(
x
)
y
0
1
1
1
2
1
удовлетворяют (1):
w (x)
y1 y2 y1 y2 + p1 ( x) y1 y2 y1 y2 0.
w(x)
Вронскиан функций у1(х) и у2(х) удовлетворяет ДУ:
ln w p1 (t )dt ln C
0
Из нач. усл. w0 = w(x0):
С=w0
формула Остроградского–
x
Лиувилля
p1 ( t ) dt
x0
x
w
ln p1 (t )dt
C
x
w ( x ) p1 ( x ) w( x ) 0.
x
dw
p1 ( x)dx
w
Пусть w≠0
w ( x) y1 y 2 y1 y 2
0
w( x) w0 e x0
w(x)
5|12
0 х
(а, b)

6.

.
Замечание. Если w(x) = 0 хотя бы в одной точке х0
х (а, b).
ЛОДУ n-го порядка
y
(n)
p n 1 ( x) y
( n 1)
(а, b), то w(x)
0 при
... p1 ( x) y p 0 ( x) y 0
(2)
p 0 ( x), p1 ( x), … pn 1 ( x) – непрерывные функции в интервале (а, b)
Теорема. Пусть в интервале (а, b) функции у1(х), у2(х),…, уn(х) являются решениями ЛОДУ (2).
Тогда справедливы утверждения:
1) если определитель Вронского w(x) 0 хотя бы в одной точке х (а, b),
то решения у1(х), у2(х),…, уn(х) – линейно независимые;
2) если решения у1(х), у2(х),…, уn(х) линейно независимые
в интервале (а, b), то определитель Вронского w(x) 0
в этом интервале.
Пример 3.
Функции 1, х, х2 –решения ДУ
y 0
1 x x2
w( x) 0 1 2 x 2 0
00 2
6|12
Критерий
проверки
линейной
зависимости
функций.
Функции 1, х, х2
линейно независимы на
всей числовой оси

7.

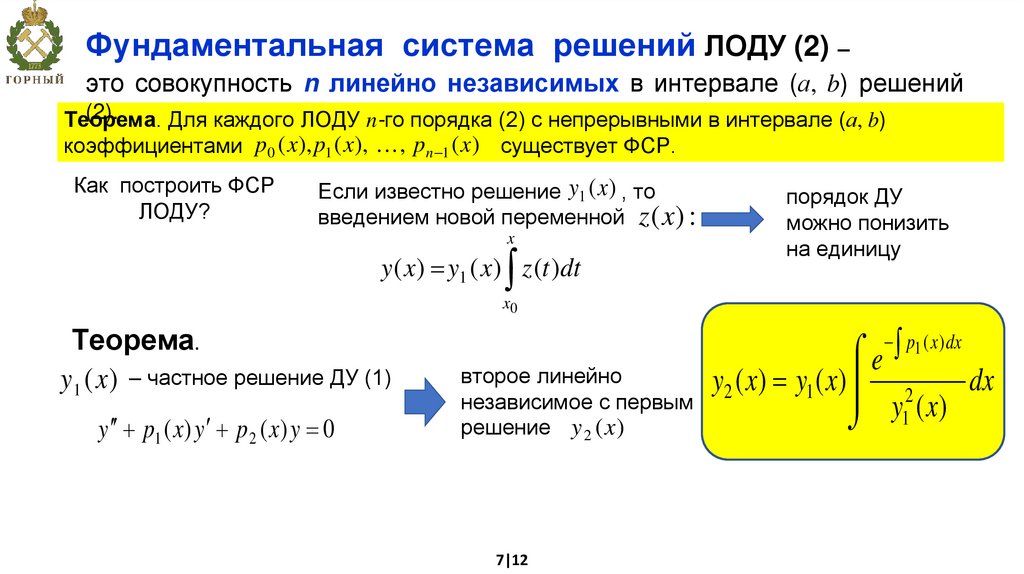
Фундаментальная система решений ЛОДУ (2) –
это совокупность n линейно независимых в интервале (а, b) решений
(2).
Теорема.
Для каждого ЛОДУ n-го порядка (2) с непрерывными в интервале (а, b)
коэффициентами p0 ( x), p1 ( x), , pn 1 ( x) существует ФСР.
Как построить ФСР
ЛОДУ?
Если известно решение y1 ( x) , то
введением новой переменной z (x ) :
x
y ( x) y1 ( x) z (t )dt
порядок ДУ
можно понизить
на единицу
x0
Теорема.
y 1 ( x ) – частное решение ДУ (1)
y p1 ( x) y p 2 ( x) y 0
p1 ( x ) dx
e
второе линейно
y2 ( x) y1 ( x) 2
dx
y1 ( x)
независимое с первым
решение y 2 ( x)
7|12

8.

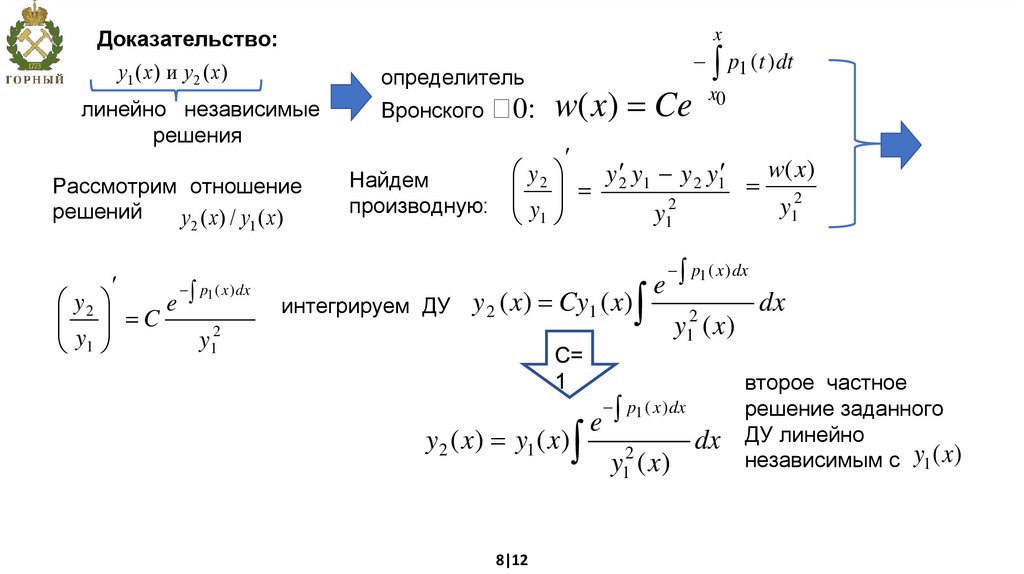
Доказательство:
x
y1 ( x ) и y2 ( x )
определитель
линейно независимые
решения
Рассмотрим отношение
решений
y ( x) / y ( x)
2
Найдем
производную:
1
p1 ( x ) dx
y2
e
C
2
y
y
1
1
Вронского
интегрируем ДУ
0: w( x) Ce
p1 ( t ) dt
x0
y2
y 2 y1 y 2 y1 w( x)
2
2
y
1
y1
y1
y 2 ( x) Cy1 ( x)
y2 ( x) y1 ( x)
8|12
e
e
p1 ( x ) dx
y ( x) dx
2
1
p1 ( x ) dx
y ( x) dx
2
1
второе частное
решение заданного
ДУ линейно
независимым с y1 ( x)

9.

Пример 4. Функция у=х – частное решение ДУ:
y y
y 2 0.
x x
Найти 2-ое частное решение, которое линейно независимо с 1–ым.
1
1
p1 ( x) , p 2 ( x) 2 – непрерывны для x>0 ищем решение ДУ
x
x
в интервале (0, )
y2 ( x) y1 ( x)
e
p1 ( x ) dx
2
y1 ( x)
y 2 ( x) x
dx
dx =lnх
x
e
x
2
dx e
ln x
1
x x dx x ln x
x
y1 ( x) x y2 ( x) x ln x
линейно независимые
решения
Определитель
Вронского:
x
x ln x
y1 y 2
x 0
w( x)
1 1 ln x
y1 y 2
9|12

10.

Теорема о структуре общего решения.
Функции
y1 ( x ) и y2 ( x )
линейно независимые решения ДУ (1)
общее решение
имеет вид:
y ( x) p1 ( x) y ( x) p2 ( x) y ( x) 0
Доказательство
y1 ( x ) и y2 ( x ) – ФСР ДУ
y ( x) C1 y1 ( x) C2 y2 ( x)
C1 ,C2 – произвольные постоянные
y ( x) C1 y1 ( x) C2 y2 ( x) – решение ДУ
При любых начальных условиях: y ( x 0 ) y 0 , y ( x0 ) y0
можно подобрать значения постоянных, чтобы решение удовлетворяло заданным
начальным условиям
система линейных
C
y
(
x
)
C
y
(
x
)
y
,
1 1 0
C1 , C 2 неизвестные
2 2 0
0
алгебраических
C1 y1 ( x0 ) C2 y2 ( x0 ) y0 . уравнений
Определитель системы –
определитель Вронского
для функций y1 ( x ) и y2 ( x ) при х=х0
определитель
системы
0
10|12
система имеет
единственное
решение

11.

y
(n)
p n 1 ( x) y
( n 1)
... p1 ( x) y p 0 ( x) y 0
y1 ( x), y2 ( x), , yn ( x) – ФСР ЛОДУ n-го порядка
общее
решение
y ( x) C1 y1 ( x) C2 y2 ( x) Cn yn ( x)
C1 , C2 , , Cn – произвольные
постоянные
sin
x
2
Пример 5. Для уравнения y y y 0 известно частное решение y1 ( x )
.
x
x
p
(
x
)
dx
2
1
e
Построить общее решение уравнения p1 ( x) x
y2 ( x) y1 ( x)
dx
2
y1 ( x)
Найдем второе частное решение
2
dx
x
cos x
sin x
dx sin x ( ctgx)
sin x e
2
2
ln
x
2
y 2 ( x)
x
dx
e
x
2
x
x
x
sin x
x
sin 2 x
общее решение ДУ: y ( x ) C1
11|12
sin x
cos x
C2
.
x
x

12.

Спасибо за внимание
Кафедра высшей математики;
Санкт-Петербургский горный
университет императрицы
Екатерины II;
199106, Санкт-Петербург,
Васильевский остров, 21 линия д.2;
Тел.: +7(812) 328-82-31;
E-mail: kafmatem@spmi.ru
12|12