В журнал Свойства параллельных плоскостей (1)

1.

Геометрия 10 класс
Тема:
«Свойства параллельных
плоскостей»

2.

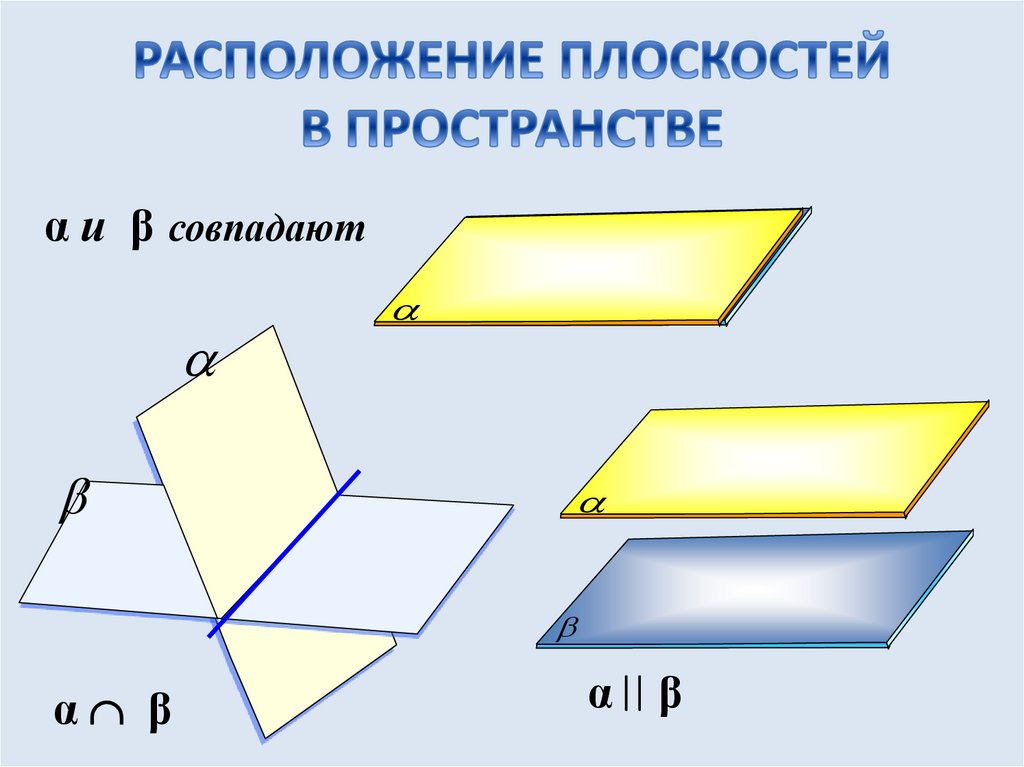
α и β совпадают
α β
α β

3.

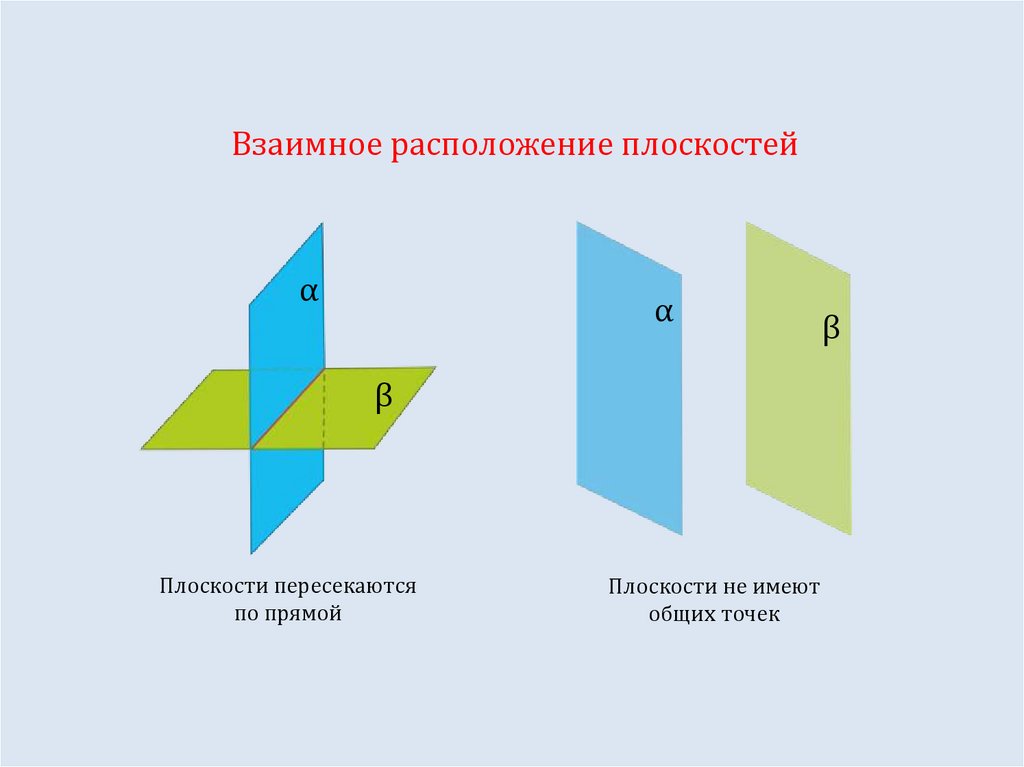
Взаимное расположение плоскостей
α
α
β
Плоскости пересекаются
по прямой
Плоскости не имеют
общих точек
β

4.

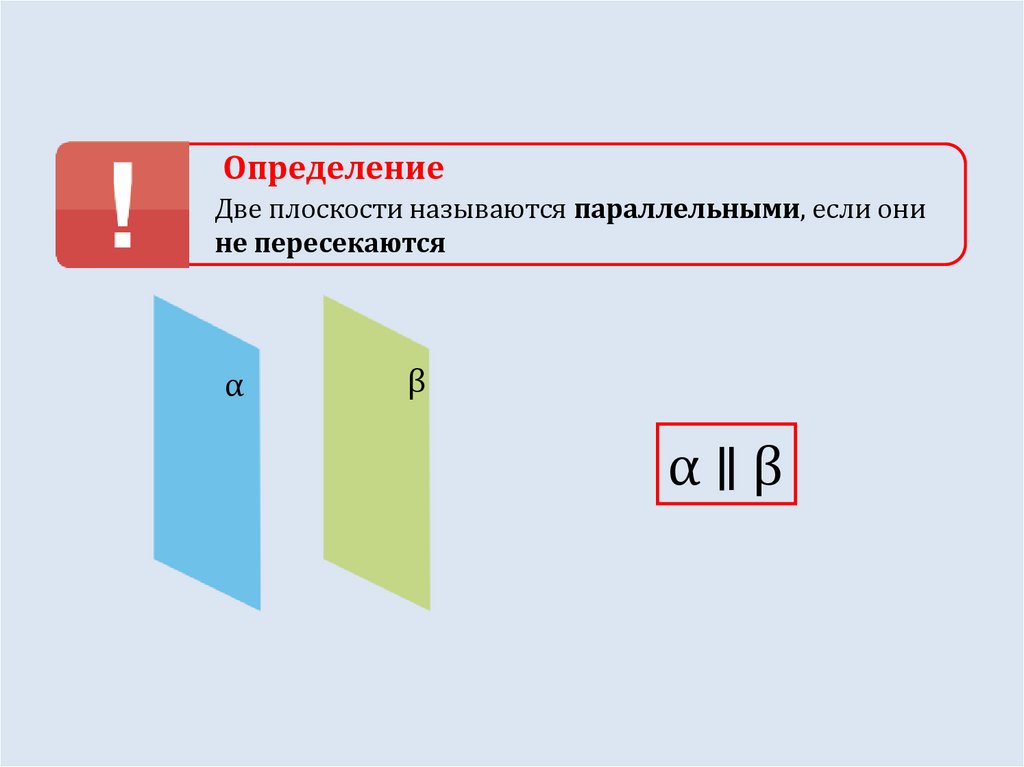
Определение
Две плоскости называются параллельными, если они
не пересекаются
α
β
α∥β

5.

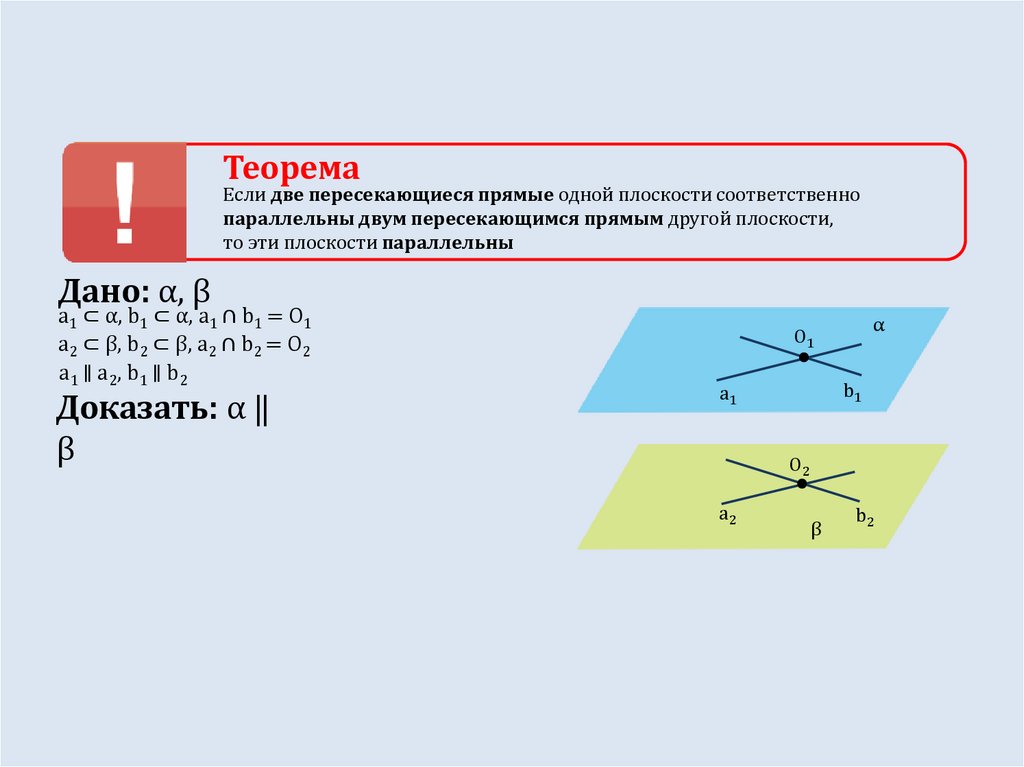
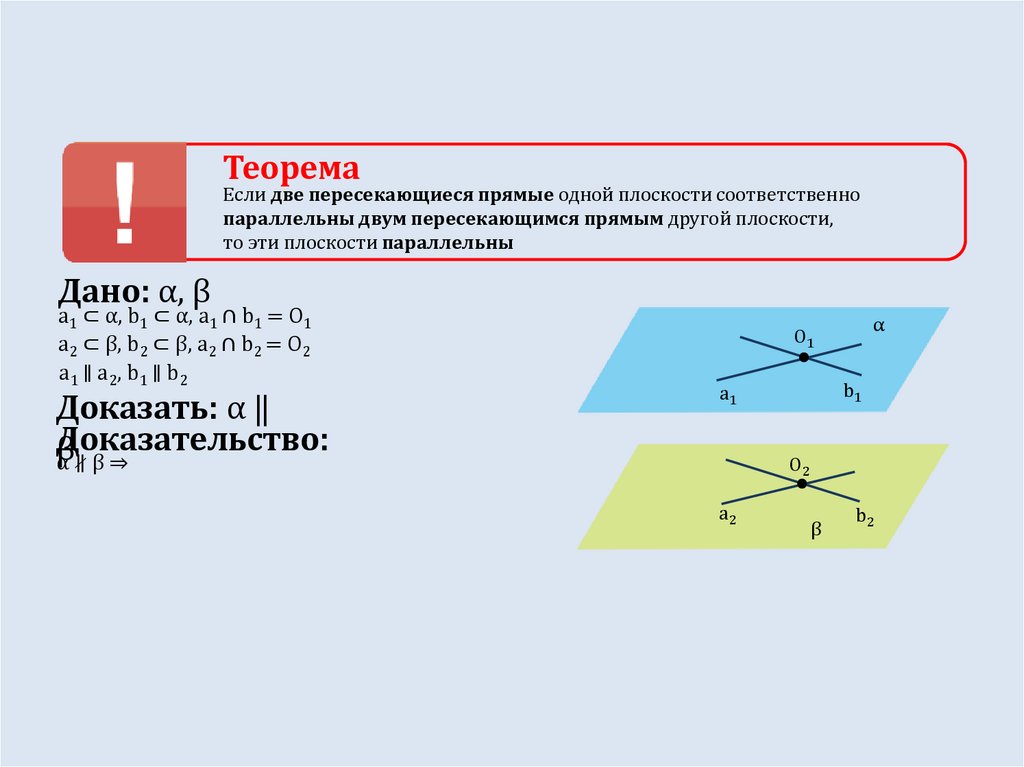
Теорема
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
Доказать: α ‖
β
α
O1
b1
a1
O2
a2
β
b2

6.

Теорема
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
Доказать: α ‖
Доказательство:
β
α∦β⇒
α
O1
b1
a1
O2
a2
β
b2

7.

Теорема
Если две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
c
Доказать: α ‖
Доказательство:
β
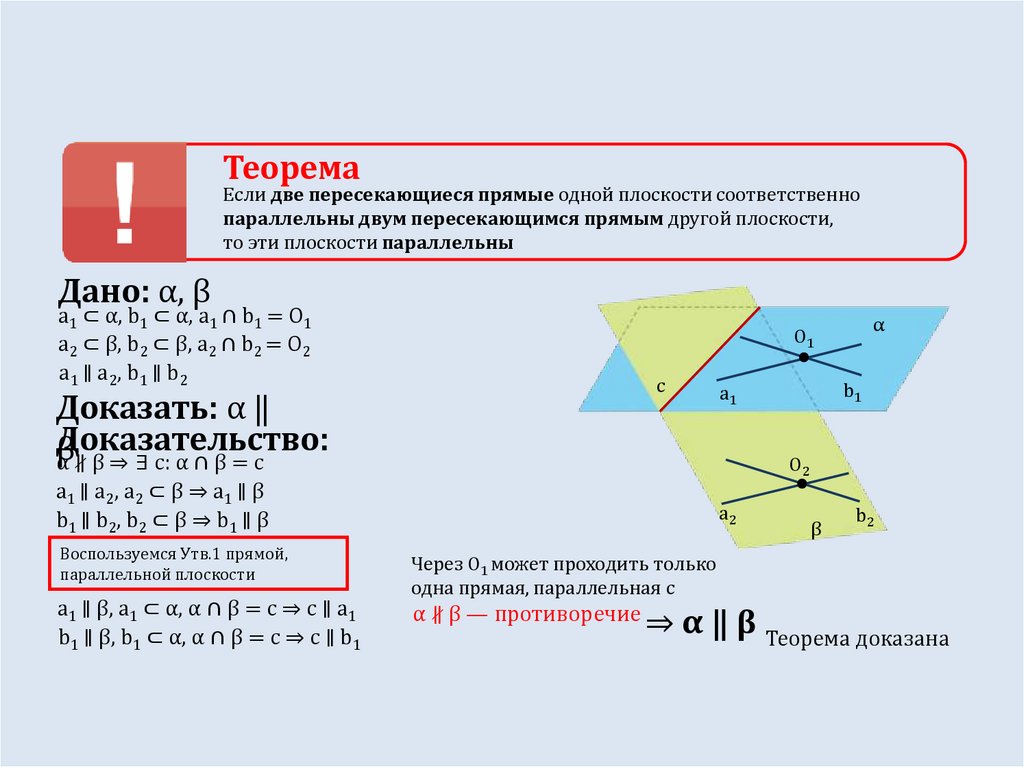
α ∦ β ⇒ ∃ c: α ∩ β = c
a1 ∥ β, a1 ⊂ α, α ∩ β = c ⇒ c ∥ a1
b1 ∥ β, b1 ⊂ α, α ∩ β = c ⇒ c ∥ b1
b1
a1
O2
a1 ∥ a2, a2 ⊂ β ⇒ a1 ∥ β
b1 ∥ b2, b2 ⊂ β ⇒ b1 ∥ β
Воспользуемся Утв.1 прямой,
параллельной плоскости
α
O1
a2
β
b2
Через O1 может проходить только
одна прямая, параллельная с
α ∦ β — противоречие
⇒ α ‖ β Теорема доказана

8.

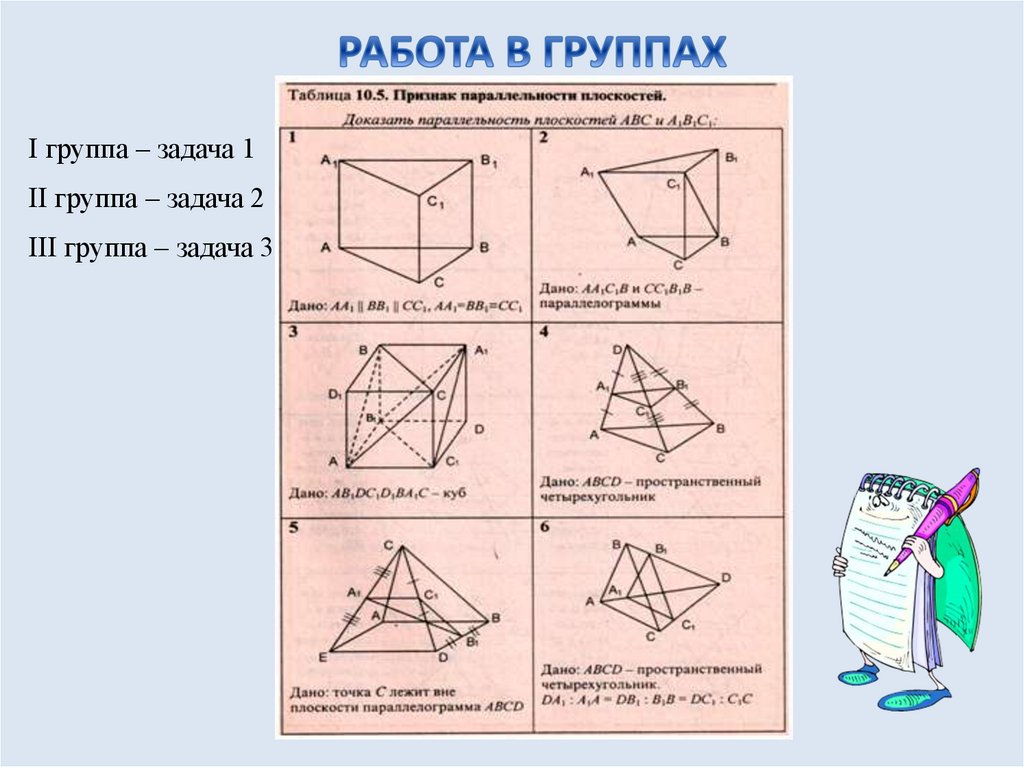
I группа – задача 1
II группа – задача 2
III группа – задача 3