Занятие 5n

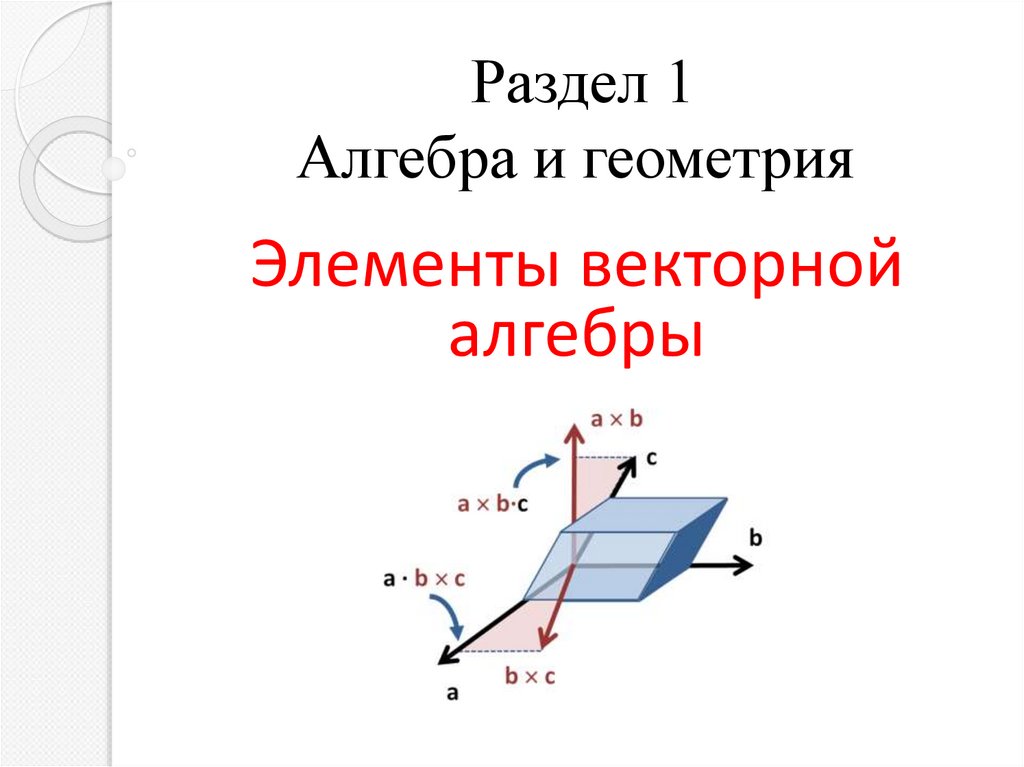
1. Раздел 1 Алгебра и геометрия

Элементы векторной
алгебры

2. Занятие 3

Учебные вопросы
1. Векторы и действия над ними.
2. Скалярное произведение векторов.
В
D
А
C

3. 1. Векторы и действия над ними

Векторные величины (векторы) – это
такие величины, которые характеризуются
не только своими числовыми значениями,
но и направлением.
Для изображения векторных величин
служат геометрические векторы.
Геометрический вектор – это
направленный отрезок.

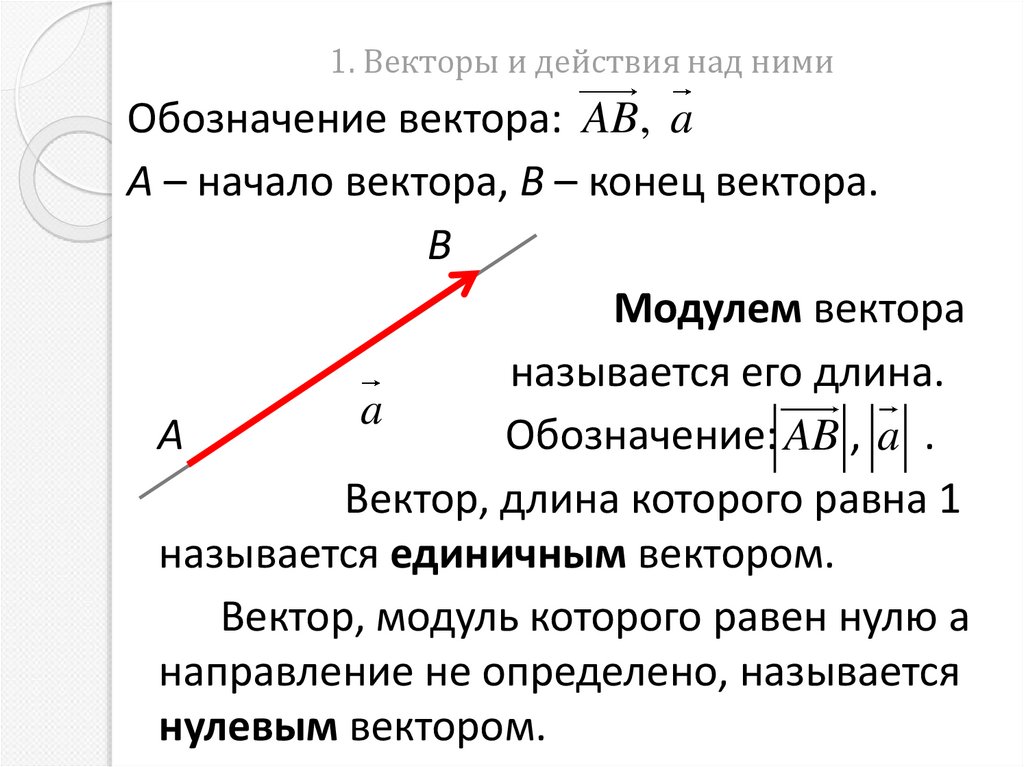
4. 1. Векторы и действия над ними

Обозначение вектора: AB, a
А – начало вектора, В – конец вектора.
В
Модулем вектора
называется его длина.
a
А
Обозначение: AB , a .
Вектор, длина которого равна 1
называется единичным вектором.
Вектор, модуль которого равен нулю а
направление не определено, называется
нулевым вектором.

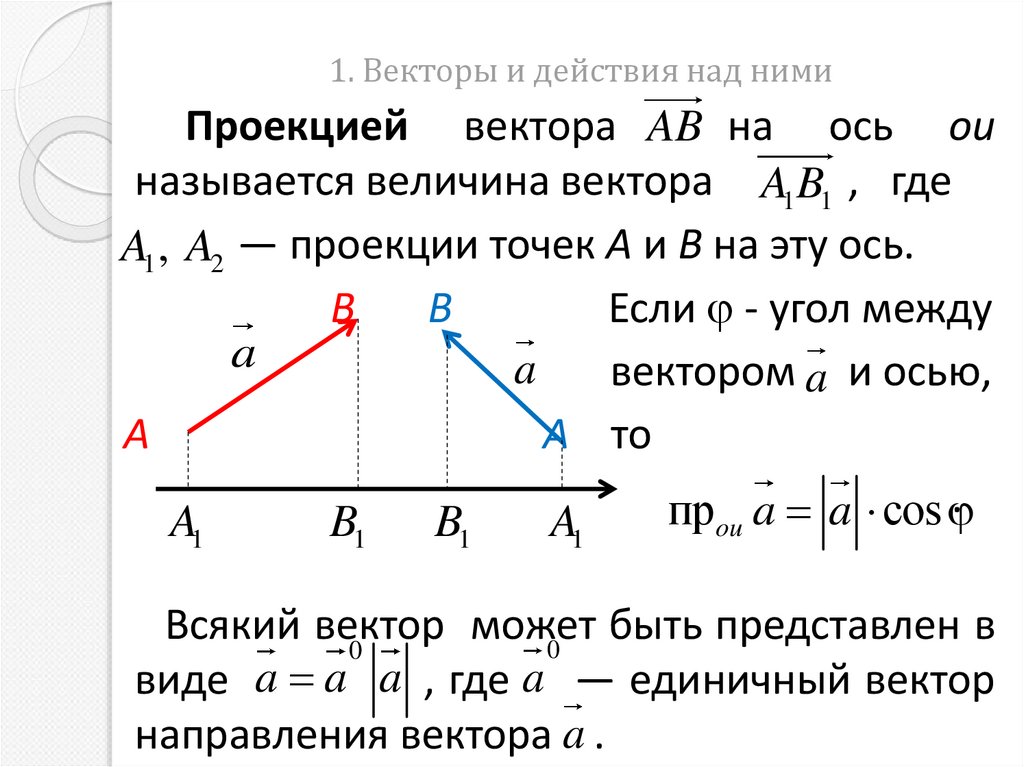
5. 1. Векторы и действия над ними

Проекцией вектора AB на ось ou
называется величина вектора A1B1 , где
A1 , A2 — проекции точек А и В на эту ось.
В
В
Если - угол между
a
a
вектором a и осью,
А
А то
.
пр
a
a
cos
A1
B1 B1
A1
ou
Всякий вектор
может
быть представлен в
0
0
виде a a a , где a — единичный вектор
направления вектора a .

6. 1. Векторы и действия над ними

Координатами вектора относительно
прямоугольной системы координат Оxyz
называются проекции ax , a y , az вектора на
оси координат. Запись a ax , a y , az
означает, что вектор a имеет координаты
ax , a y , az
z
Разложение вектора
a
по
базису
:
a
i
,
j
,
k
k
у
a ax i a y j az k
i
j
х

7. 1. Векторы и действия над ними

Направляющими косинусами вектора
называются
косинусы
углов , , ,
образованных этим вектором с осями
координат Оx, Оy, Оz.
Направляющие косинусы находятся по
формулам:
ay
ax
az
cos , cos , cos
a
a
a
Координаты единичного вектора равны
его направляющим косинусам.

8. 1. Векторы и действия над ними

Модуль вектора находится по формуле
a ax2 a y2 az2 .
Нахождение проекций вектора
по известным координатам его начала и конца
Рассмотрим вектор AB a , пусть даны
координаты его начала и конца, то есть
координаты точек А и В: A xA , y A , z A ,B xB , yB , zB .
Тогда
a x xB x A , a y y B y A , a z z B z A
и модуль вектора
a
xB x A y B y A z B z A
2
2
2
.

9. 1. Векторы и действия над ними

Пример
Даны две точки A 2; 1;3 , B 3;1; 3
. Найти
координаты вектора
, его модуль и
AB
направляющие косинусы.
Решение
AB 1;2; 6 , AB 1 4 36 41,
1
2
6
cos
, cos
, cos
.
41
41
41

10. Занятие 5

Учебные вопросы
1. Векторное произведение векторов.
2. Смешанное произведение векторов.
В
D
F
А
C
Е

11. 1. Векторное произведение векторов

Векторным произведением вектора a на
вектор b называется вектор, обозначаемый
символом а b или a, b , определяемый
условиями:
1. модуль этого вектора а b a b sin ;
2. этот вектор перпендикулярен каждому из
перемножаемых векторов, т.е плоскости,
определяемой этими векторами;
3. направлен по перпендикуляру к
плоскости так, что векторы a, b и a b
составляют правую тройку .

12. 1. Векторное произведение векторов

Геометрический смысл модуля
векторного произведения:
a b a b sin S ,
т.е. модуль векторного произведения
численно равен площади
параллелограмма,
построенного на векторах
сомножителях.
S

13. 1. Векторное произведение векторов

Свойства векторного произведения
1. a b b a .
2. (a b ) a b a b .
3. (a b ) c a c b c .
4. векторное произведение равно нулю
тогда и только тогда, когда один из
векторов равен нулю или векторы
коллинеарны.
Необходимое и достаточное условие
коллинеарности векторов a и b является
условие a b 0.

14. 1. Векторное произведение векторов

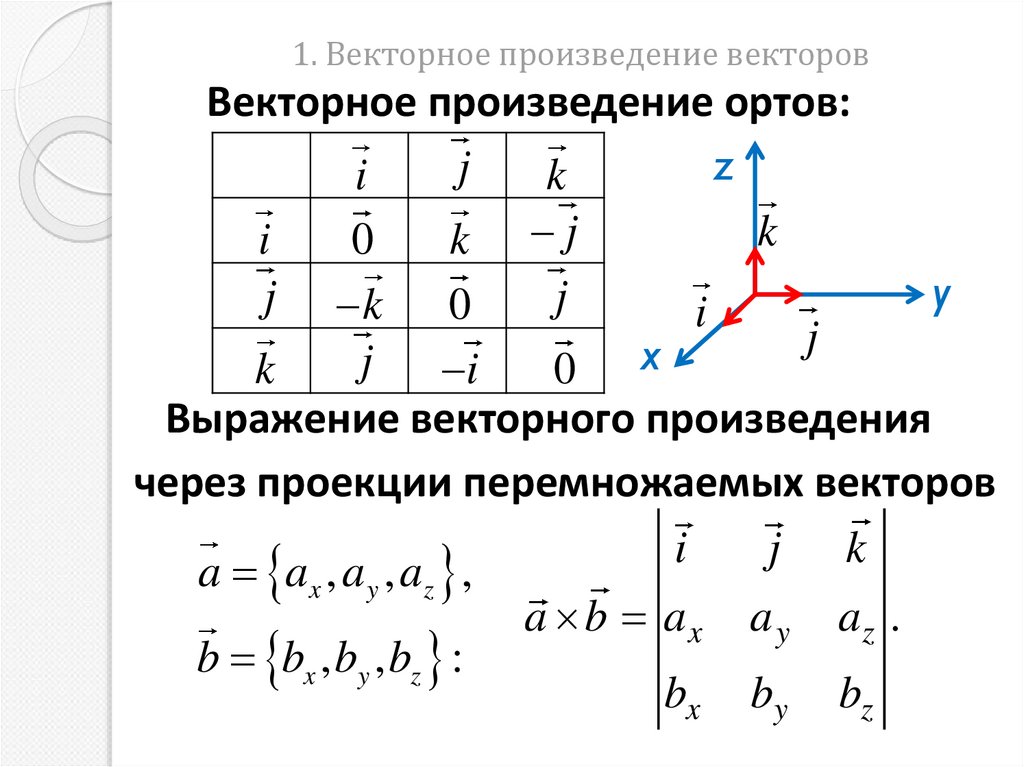
Векторное произведение ортов:
z
j
i
k
k
0
i
k j
y
j k 0
j
i
j
j i
0 x
k
Выражение векторного произведения
через проекции перемножаемых векторов
i
j k
a ax , a y , az ,
a b ax a y az .
b bx , by , bz :
bx by bz

15. 1. Векторное произведение векторов

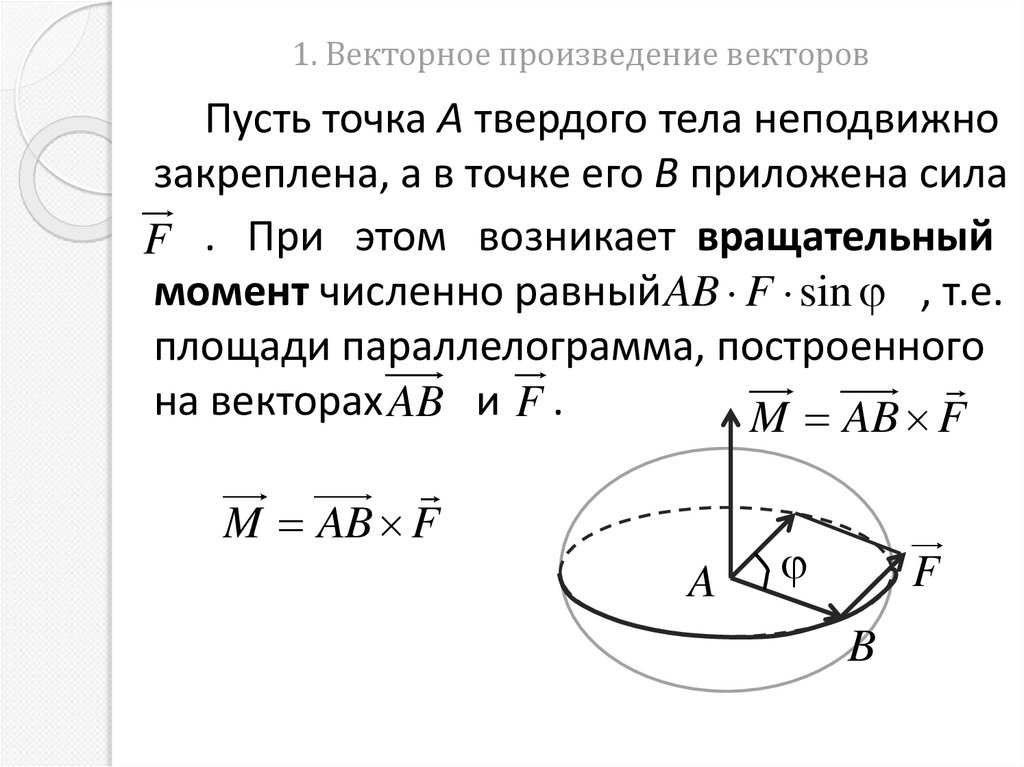
Пусть точка А твердого тела неподвижно
закреплена, а в точке его В приложена сила
F . При этом возникает вращательный
момент численно равный AB F sin , т.е.
площади параллелограмма, построенного
на векторах AB и F .
M AB F
M AB F
A
А
F
B

16. 1. Векторное произведение векторов

Пример 1
Найти площадь треугольника с вершинами
В
A 1;2;3 , B 2;1;4 , C 0; 3;4 .
Решение
1
S AB AC
2
AB 3, 1,1 , AC 1, 5,1
А
С
i
j k
AB AC 3 1 1 4i 2 j 14k ,
1 5 1
1
1
S AB AC
16 4 196 3 6
2
2

17. 1. Векторное произведение векторов

Пример 2
Точка А(4,-1,3) твердого тела закреплена. В
точке его В(0,3,5) приложена силаF 2,0,1 .
Найти момент силы относительно точки А и
его величину.
Решение: AB 4,4,2 ,
i
j k
M AB F 4 4 2 4i 8 j 8k ,
2 0 1
M 16 64 64 12.

18. 1. Векторное произведение векторов

Задание
Найти площадь параллелограмма,
построенного на векторах a 8;4;1 и
b 2; 2;1 .

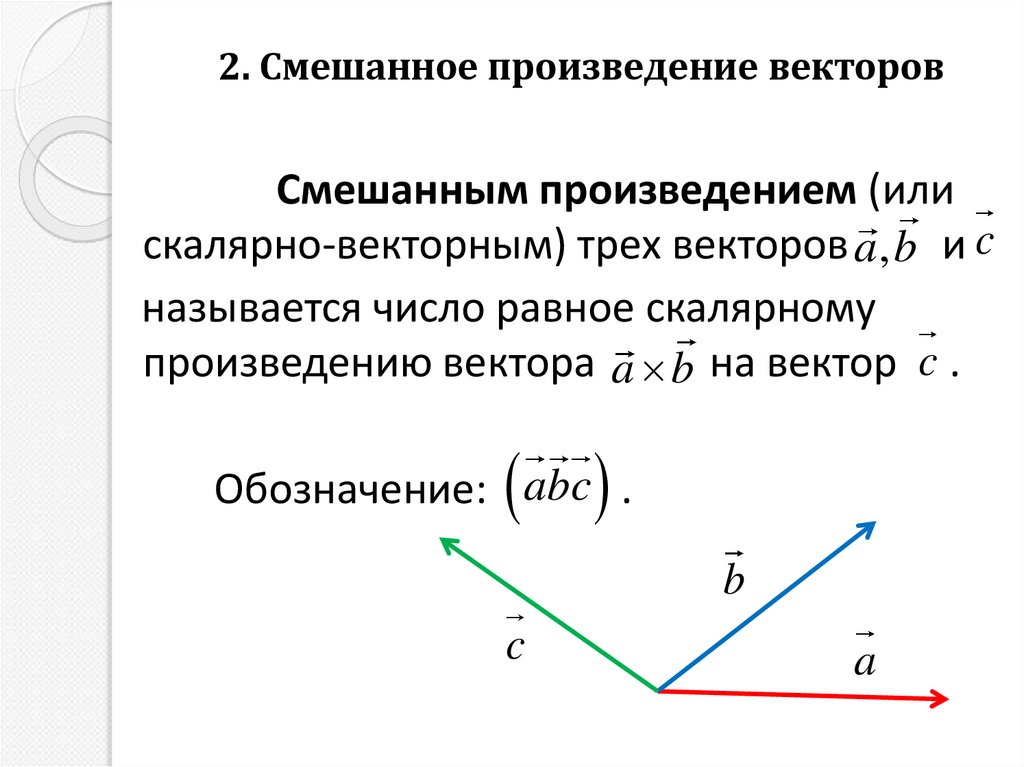
19. 2. Смешанное произведение векторов

Смешанным произведением (или
скалярно-векторным) трех векторов a , b и c
называется число равное скалярному
произведению вектора a b на вектор c .
Обозначение: abc .
b
c
a

20. 2. Смешанное произведение векторов

Выражение смешанного произведения 3х векторов a, b и c через координаты
сомножителей:
a ax , a y , az , b bx , by , bz , c cx , c y , cz
ax
ay
az
(abc ) bx
by
bz
cx
cy
cz

21. 2. Смешанное произведение векторов

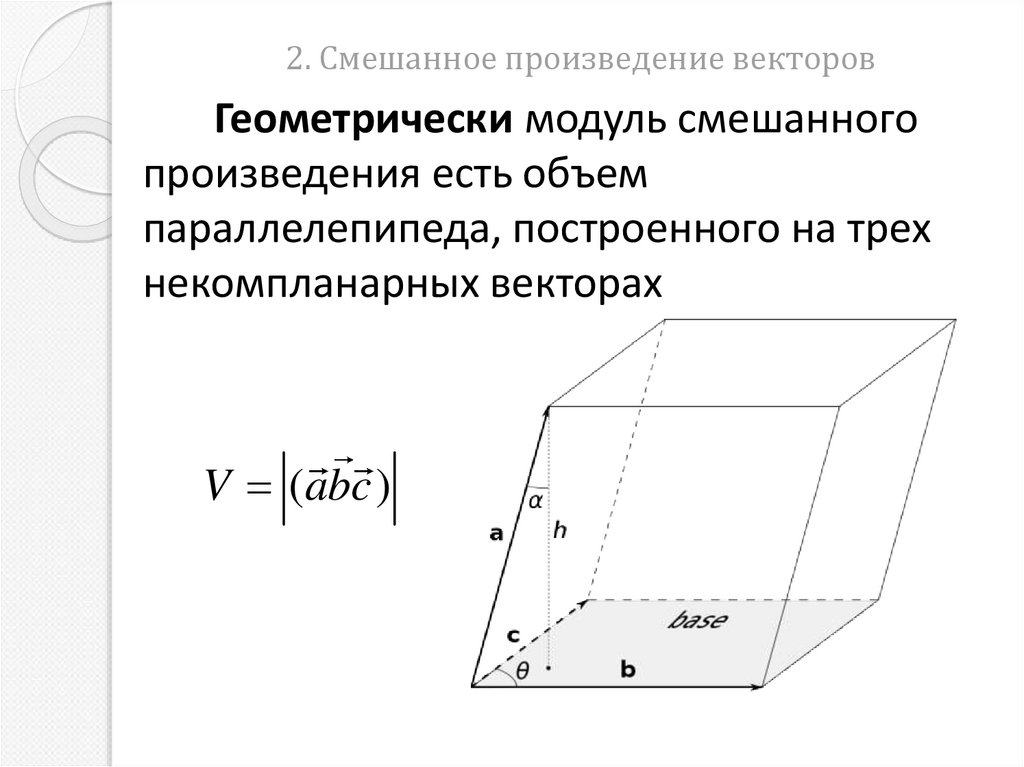
Геометрически модуль смешанного
произведения есть объем
параллелепипеда, построенного на трех
некомпланарных векторах
V (abc )

22. 2. Смешанное произведение векторов

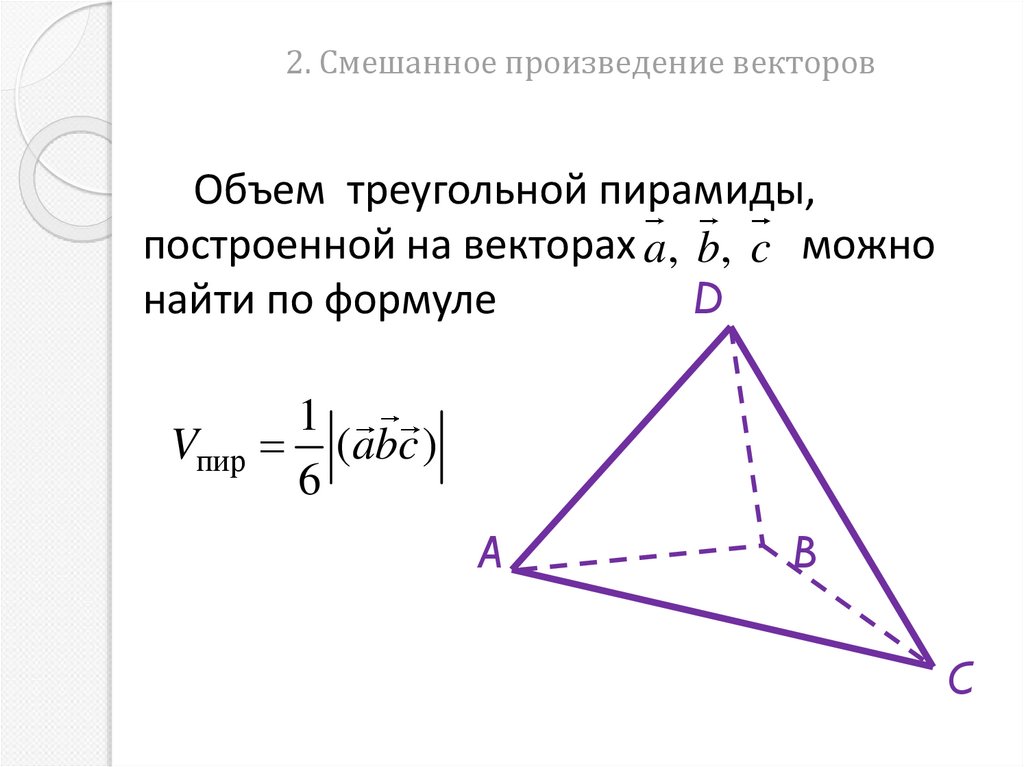
Объем треугольной пирамиды,
построенной на векторах a, b, c можно
найти по формуле
D
1
Vпир (abc )
6
A
B
C

23. 2. Смешанное произведение векторов

Свойства смешанного произведения
2. a b c b c a c a b
3. a b c a b c
4. abc 0 , если среди сомножителей
1. abc bac cba acb
есть хотя бы один нуль-вектор, если по
крайней мере два из перемножаемых
векторов коллинеарны, или если векторы
a, b, c компланарны.

24. 2. Смешанное произведение векторов

Необходимое и достаточное условие
компланарности векторов a, b, c:
abc 0.
Пример
Проверить, компланарны ли данные
векторы a 1;2; 2 , b 1; 2;1 , c 5; 2; 1
Решение:
1 2 2 1 0 0
abc 1 2 1 1 4 3 36 36 0
5 2 1
5 12 9

25. 2. Смешанное произведение векторов

Пример. Даны вершины тетраэдра A 2;3;1 ,
B 4;1; 2 ,C 6;3;7 , D 5; 4;8 . Найти
объем тетраэдра, площадь основания АВС,
длину его высоты, опущенной из вершины D.
Решение: (в учебнике!)

26. Домашнее задание

1.
Решить учебные задания.

27. До свидания