презентация по ППП, ФОМНЭ - 2 (1)

1.

Учебная дисциплина
«Полупроводниковые приборы»,
ФОМНЭ

2.

И н д е кс ы М и л л е р а .
Л ю б о й уз е л к р и с т а л л и че с к о й р е ш е т к и м о ж е т б ы т ь в ы б р а н з а
начало
ко о р д и н а т .
От
него
проводят
к о о р д и н а тн ы е
оси
в
н а п р а в л е н и я х о с н о в н ы х в е кт о р о в ( a , b , c ) , с о в п а д а ю щ и е с р ё б р а м и
э л е м е н т а р н о й я ч е й к и . Т а ки е о с и н а з ы в а ю т к р и с т а л л о г р а ф и ч е с к и ми ,
а д л и н ы р ё б е р эл е м е н т а р н о й я ч е й ки – о с е в ы ми е д е н и ц а ми . М а с ш т а б
п о о с я м х , у, z в о б щ е м с л уч а е м о ж е т б ы т ь р а з л и ч н ы м .
И н д е кс ы М ил л е р а – з а п и с а н н ы е о п р е д е л ё н н ы м о б р а з о м чи с л а ,
з а д а ю щ и е п о л о ж е н и я в к р и с та л л е те х и л и и н ы х уз л о в , н а п р а в л е н и й ,
п л о с к о с те й .
а ) И н д е к с ы уз л а .
Если
за
единицу
масштаба
взять
п о с т о я н н ую
решетки,
то
к о о р д и н а т ы уз л а – э т о ч и с л а :
х = a∙u; y = b∙v; z = c∙w. Здесь u, v, w – целые числа.
[ [ u , v , w ] ] – и н д е к с ы М и л л е р а д л я уз л а
2

3.

Для
отрицательного
индекса
ставится
черта
над
индексом,
например[[u, v , w]].
Н а п р и м е р , п о л о ж е н и е ц е н т р а э л е м е н т а р н о й к уб и ч е с к о й я ч е й к и
[[1/2, 1/2, 1/2]]. Положение центра гран и, лежащей в плоскости xoy,
определяется индексом [[1/2, 1/2, 0]]
б) Индексы кристаллографических направлений.
Для
вектора
r
ua
vb
c
=
кристаллографического
+
+w
направления,
индексы
Миллера
х а р а к т е р и з уе м о г о
этим
вектором, записываются в квадратных скобках [u v w] .
Положение направления точно определяется началом отсчёта и
п о л о ж е н и е м 1 - о г о уз л а , ч е р е з к о т о р ы й о н о п р о х о д и т .
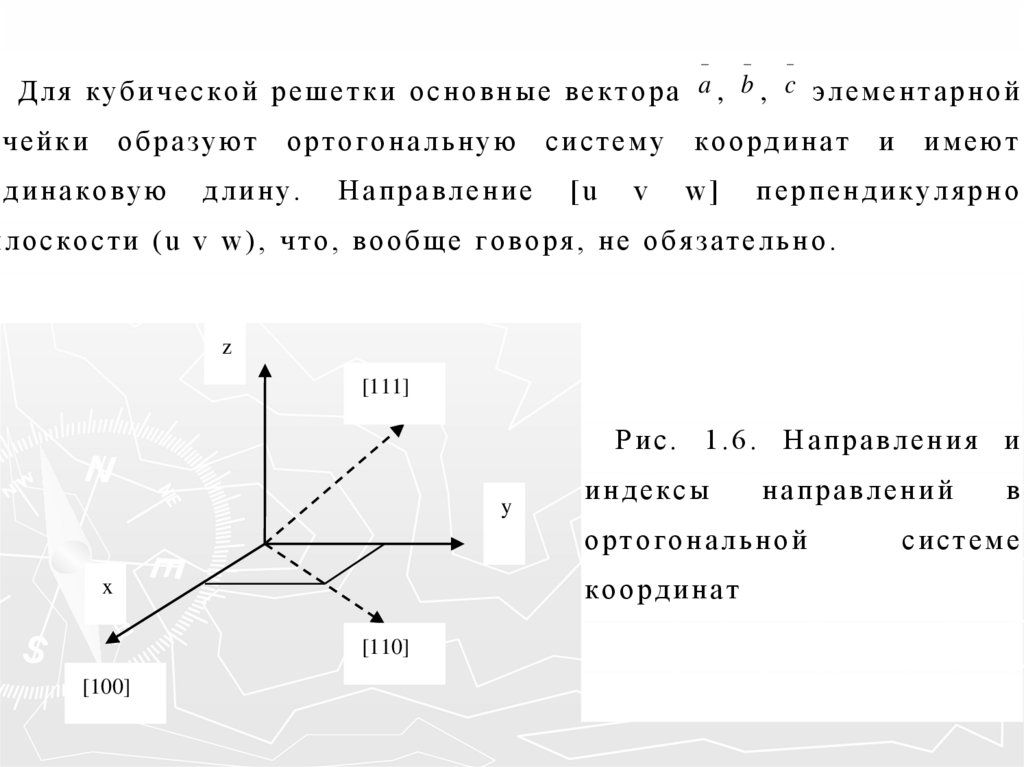
Например, индекс направления, параллельного про странственной
диагонали, записывается: [111] (рис.1.6).
Ясно, что индексы [[1/2 1/2 1]], [112], [224] и т.д. обозначают
од но и тож е на п ра в ле ни е . П оэтому , об ы чн о, и нд е кс уме н ьша ю т д о
наименьших
целых
чисел.
Для
обозначения
эквивалентных
3
кри с та лл огра фи че с ких на пра вл ени й и сп ол ьз ую т угол ьные с коб ки

4.

Д л я к уб и ч е с к о й р е ш е т к и о с н о в н ы е в е к т о р а a , b , c э л е м е н т а р н о й
ячейки
о б р а з ую т
о д и н а к о в ую
ортогональную
д л и н у.
Направление
систему
[u
v
координат
w]
и
имеют
п е р п е н д и к ул я р н о
плоскости (u v w), что, вообще говоря, не обязательно.
z
[111]
Рис. 1.6. Направления и
y
индексы
направлений
ортогональной
в
системе
координат
x
[110]
[100]
4

5.

в) Индексы кристаллографических плоскостей.
Кроме
уз л о в
идентичных
и
направлений
решетка
кристаллографических
содержит
плоскостей,
множество
также
определяющих свойства кристалла: пластическую деформацию и
др.
свойства;
рост
и
скол
кристаллов
легче
происходит
по
определенным плоскостям.
Плоскость
может
быть
задана
либо
п е р п е н д и к ул я р н ы м
направлением к ней [u v w], либо отрезками, отсекаемы ми на
координатных осях (рис. 1.7 ).
В п о с л е д н е м с л у ч а е ур а в н е н и е п л о с к о с т и и м е е т в и д
x y z
1
u v w
,
г д е к о о р д и н а т н ы е о с и x , y, z п е р е с е к а ю т с я в т о ч к а х u , v , w . Э т о
уравнение может быть пе реписано:
hx + ky + lz = 1,
5

6.

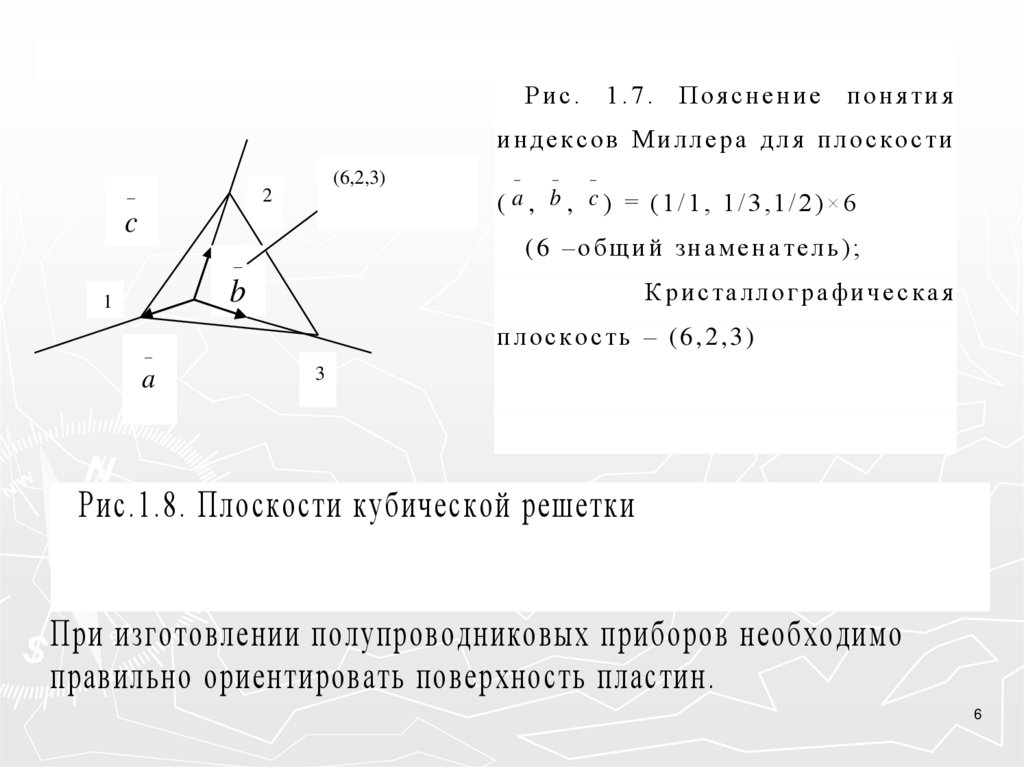
Рис.
1.7.
Пояснение
понятия
индексов Миллера для плоскости
(6,2,3)
2
( a , b , c ) = (1/1, 1/3,1/2)×6
c
(6 –общий знаменатель);
Кристаллографичес кая
b
1
плоскость – (6,2,3)
a
3
Рис.1.8. Плоскости кубической решетки
При изготовлении полупроводниковых приборов необходимо
правильно ориентировать поверхность пластин.
6

7.

Каждой
плотность
кристаллографической
атомов
на
единицу
плоскости
площади.
свойственна
Если
своя
посмотреть
на
к р и с т а л л с к уб и ч е с к о й р е ш е т к о й п е р п е н д и к ул я р н о й п л о с к о с т я м
( 1 0 0 ) , ( 1 1 0 ) , ( 1 1 1 ) , т о р а с п о л о ж е н и е а т о м о в в п о л е з р е н и я б уд е т
различным (рис. 1.9 ).
Рис.
1.9.
Расположение
атомов
в
отдельных
плоскостях
к уб и ч е с к о й р е ш е т к и .
Наименьшая
и
наибольшая
плоскости
ат омов
б уд у т ,
соответственно, в плоскостях (100) и (111). У Si плоскость (111)
является
плоскостью
спайности,
в
ней,
как
правило,
распространяются трещины, и происходит раскалывание кристалла 7
именно по этой плоскости.

8.

Статистика носителей заряда в полупроводниках.
Частицы, образующие систему, могут иметь различную энергию, то есть
находиться в разных энергетических состояниях. Важно соотношение: Ι – число
возможных энергетических состояний и ΙΙ – число частиц, способных их
занять. Если Ι >> ΙΙ, то система называется невырожденной, у частиц имеется
большой выбор состояний, маловероятно, что в одном из них окажется сразу
несколько частиц. Такие системы подчиняются законам классической
статистики Максвелла-Больцмана.
Если же Ι ≤ ΙΙ, то весьма вероятна встреча микрочастиц в одном состоянии,
система в этом случае называется вырожденной. Подобные системы
подчиняются законам квантовой статистики. В вырожденных системах
возможность заполнения состояний определяется природой частиц. С этой
точки зрения все микрочастицы делятся на две группы:
- фермионы; это микрочастицы, подчиняющиеся принципу Паули, например
электроны. Если данное состояние уже занято фермионом, то другой фермион его 8
занять не сможет. Фермионы описываются статистикой Ферми-Дирака;

9.

- бозоны; это частицы, которые могут в неограниченном количестве занимать одно и то
же состояние. К ним относятся, например, фотоны и фононы. Бозоны описываются
статистикой Бозе-Эйнштейна.
Статистические функции распределения (статистики) показывают с какой
вероятностью f (ε, Т) частица при температуре Т будет обладать энергией ε.
Невырожденные системы описываются статистикой Максвелла-Больцмана
f (ε, Т) = еxp [- ( ε- εF) / kT],
где к – постоянная Больцмана, εF – энергия Ферми. Эту
статистику называют классической.
С термодинамической точки зрения энергия Ферми εF соответствует химическому
потенциалу системы. Смысл таков: для изолированной системы постоянного объёма, не
получающей и не отдающей тепловую энергию, изменение внутренней энергии dε
пропорционально изменению числа частиц dN в системе. Коэффициент
пропорциональности К = dε/ dN – это химический потенциалом системы. Он численно
равен работе, которую надо затратить, чтобы увеличить число частиц в системе на
еденицу. Таким образом К = εF. Во всех частях системы, находящейся в состоянии
термодинамического равновесия, уровень ε занимает единое положение.
9

10.

Число электронов в зоне проводимости и дырок в валентной зоне обычно
значительно меньше числа энергетических состояний, содержащихся в этих зонах.
Поэтому средняя плотность заполнения энергетических состояний электронами и
дырками f соответствует неравенству.
f << 1. (2.28)
Если это условие выполняется, полупроводник является невырожденным, если,
наоборот, не выполняется - вырожденным
Собственный полупроводник.
При температуре Т=0К все энергетические уровни валентной зоны заполнены
электронами, а уровни зоны проводимости - свободны.
С повышением температуры некоторое количество электронов покидает валентную
зону и переходит в зону проводимости.
Распределение электронов и дырок по энергиям в твердом теле описывается
статистикой Ферми - Дирака. Согласно этой статистике вероятности того, что
состояние с некоторой энергией при температуре Т будет занято электроном,
определяется функцией Ферми - Дирака
1
f n ( , T )
F
1 exp(
)
(2.29)
10

11.

,
где - энергия, отсчитанная от произвольно выбранного уровня ,обычно
от уровня
В
энергия
Ферми,
отсчитанная относительно того же уровня;
F
k 1.38 10 23 Дж/град - постоянная Больцмана.
Вероятность выражается в долях единицы или в процентах.
Рассмотрим некоторый энергетический уровень в валентной зоне
Если он занят электроном, то f n= 1, и вероятность превратилась в
достоверность.
Если же он не занят, то эта вероятность f =
n 0.
Но вероятность того, что энергетический уровень в валентной зоне не занят
электроном, есть вероятность нахождения на этом уровне дырки f p
Таким образом, f n= 1, если f p= 0, а сумма эти вероятностей f n+ f p= 1. Отсюда
можно найти выражение для f p . Отняв от единицы выражение (2.29),
получим соотношение
f n ( , T )
1
1 exp(
F
kT
(2.30)
)
11

12.

Известно, что для описания энергетического состояния свободных электронов в
газовом разряде и в других случаях используется классическая функция распределения
Максвелла - Больцмана.
Существенным отличием функции Ферми - Дирака от функции распределения
Максвелла - Больцмана является то, что первая в отличие от последней может и
не быть непрерывной.
( F ) (2.29) и ( F ) в (2.30)
Если в
значительно превышают среднюю тепловую энергию системы (в 3 раза и более),
то в этих выражениях можно пренебречь единицей по сравнению с экспонентами.
Тогда получим:
f n ( , T ) exp[
( F )
]
kT
(2.31)
( F )
f n ( , T ) exp[
]
(2.32)
kT
Вид этих выражений показывает, что статистика Ферми - Дирака перешла в
статистику Максвелла - Больцмана. Физически это означает, что выполняется
условие (2.28), являющееся критерием невырожденности полупроводника. 12

13.

Рассмотрим некоторый интервал значений энергии d , лежащий в зоне
проводимости. Обозначим число энергетических состояний,
соответствующих энергии , которые могут быть заняты электронами,
через N ( ).
Тогда в интервале d будет N ( ) d таких состояний.
Выразив концентрацию электронов dn, имеющих энергии в интервале d ,
как произведение N ( ) d
на f n ( , T ) и интегрируя по всем значениям
энергии в зоне проводимости, найдем полное количество электронов в зоне
проводимости в единице объема:
n
c
N ( ) f n ( ,T )d (2.33)
Аналогичные рассуждения приводят к выражению для концентрации дырок
в валентной зоне:
p
p
N ( ) f p ( ,T )d
(2.34)
0
Из квантовой механики известно выражение N ( ) для в области
энергий c
4 (2mn )3 / 2
1/ 2
(2.35)
N ( )
(
)
c
3
h
13

14.

здесь m n - эффективная масса электрона в зоне проводимости.
Выражение (2.35) справедливо в узкой полосе энергий вблизи дна зоны
проводимости. После интегрирования (2.33) получаем выражение для
концентрации свободных электронов в полупроводнике:
( C F )
n N c exp
kT
(2.36)
Проведя аналогичные расчеты для дырок, получим выражение для их
концентрации:
( F В )
p N exp
kT
(2.37)
Коэффициенты N c и N в приведенных выражениях называются
эквивалентными плотностями состояний соответственно электронов и
дырок. В предположении, что все свободные электроны находятся вблизи
дна зоны проводимости, а дырки- вблизи потолка валентной зоны, их можно
3/ 2
3/ 2
рассчитать по формулам:
2 m kT
m
Nc 2
h
n
2
0.5 *1016 n T 3 / 2
m
(2.38) 14

15.

=
.
2 mp kT
N 2
2
h
3/ 2
3/ 2
mp
16
0.5 *10 T 3 / 2
m
(2.39)
В собственном полупроводнике энергетический уровень Ферми располагается
примерно посередине запрещенной зоны:
g
mp
kT N g 3
F ln kT ln
2 2 N c 2.40 2 4
mn
(2.40)
m m
С ростом температуры уровень обычно поднимается (поскольку
p
n
). Для большинства собственных полупроводников (кремния, германия и др.) в
рабочих интервалах температур этим смещением можно пренебречь. При
расчётах часто полагают N c = N . .
Тогда можно записать
= g /2 =
,
где через
обозначена
F
i
i
середина запрещенной зоны.
Найдем произведение концентраций носителей заряда в полупроводнике:
np N c exp[ ( c F ) / kT ] N exp[ ( F В ) / kT ]
N c N exp[ ( c В ) / kT ] N c N exp [ g / kT ]
(2.41)
15

16.

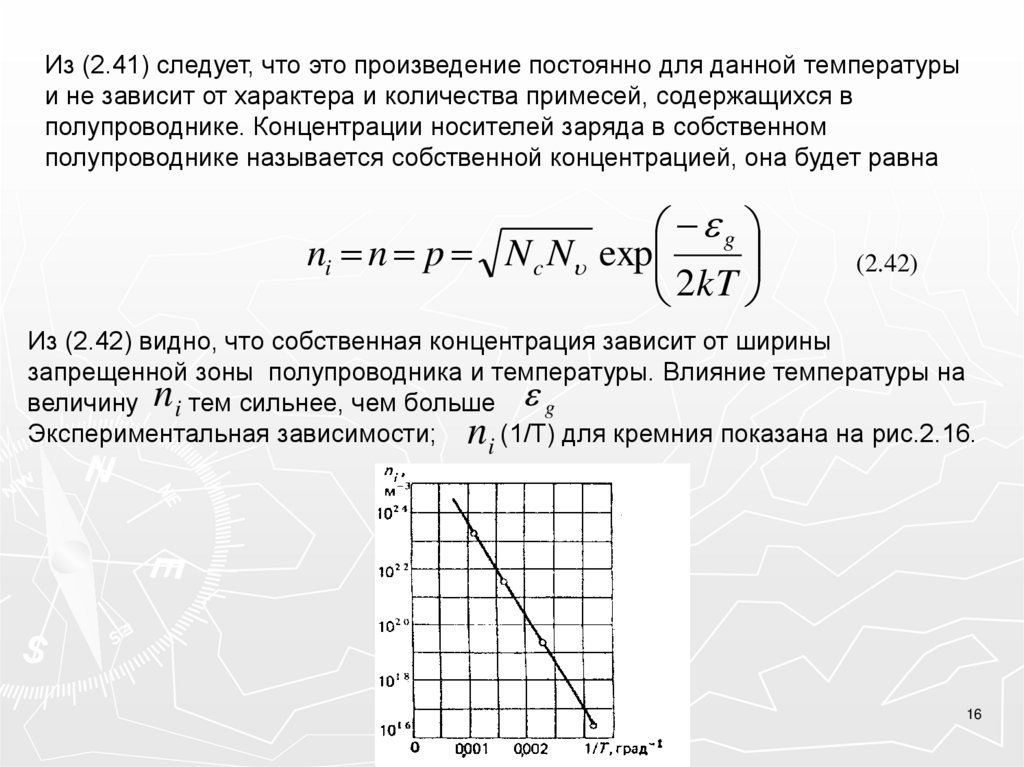
Из (2.41) следует, что это произведение постоянно для данной температуры
и не зависит от характера и количества примесей, содержащихся в
полупроводнике. Концентрации носителей заряда в собственном
полупроводнике называется собственной концентрацией, она будет равна
g
ni n p N c N exp
2kT
(2.42)
Из (2.42) видно, что собственная концентрация зависит от ширины
запрещенной зоны полупроводника и температуры. Влияние температуры на
величину ni тем сильнее, чем больше g
Экспериментальная зависимости; ni (1/Т) для кремния показана на рис.2.16.
16

17.

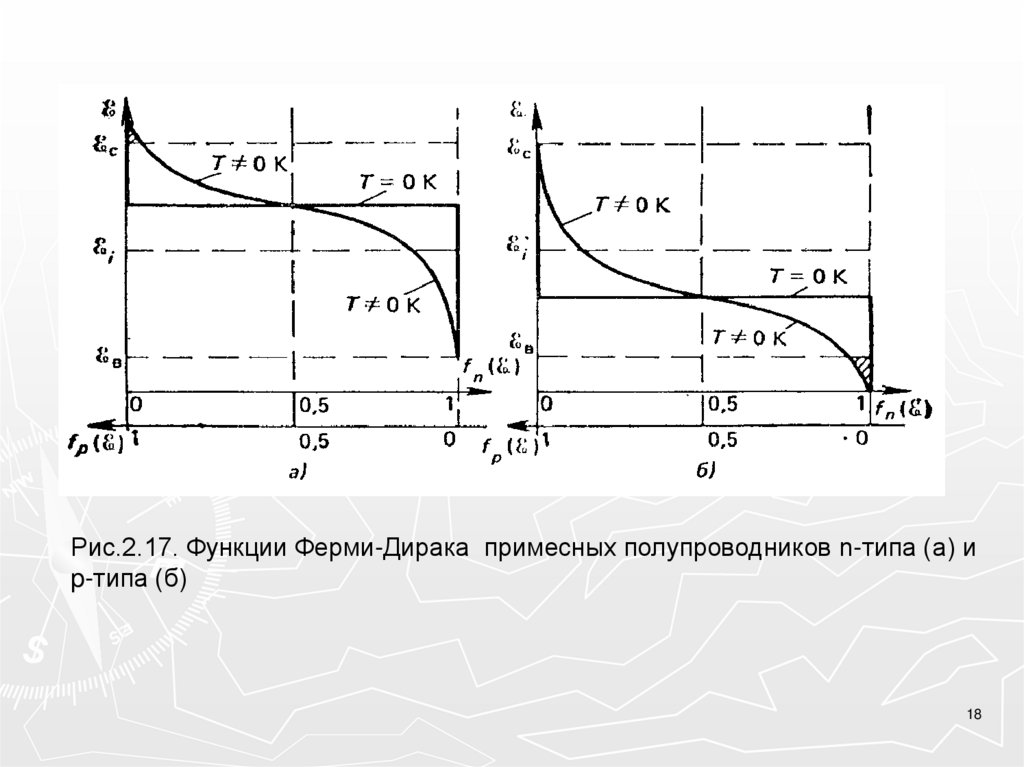
Статистика Ферми-Дирака в примесных полупроводниках.
Функция Ферми-Дирака (2.29), (2.30) справедлива не только для
собственных, но и для примесных полупроводников.
В полупроводниках n-типа большое количество электронов переходит
в зону проводимости с уровней доноров, при этом дырки в валентной
зоне не появляются.
Поэтому вероятность появления электрона в зоне проводимости выше
вероятности появления дырки в валентной зоне.
Это, очевидно, возможно в том случае, если уровень Ферми будет
смещен от середины запрещенной зоны в сторону дна зоны
проводимости. Чем выше концентрация атомов доноров в полупроводнике
, тем больше это смещение.
В полупроводнике p-типа, наоборот, уровень располагается ниже
уровня , и с повышением концентрации атомов акцепторов в нем
уровень Ферми будет располагаться все ближе к потолку валентной
зоны.
17

18.

Рис.2.17. Функции Ферми-Дирака примесных полупроводников n-типа (а) и
p-типа (б)
18

19.

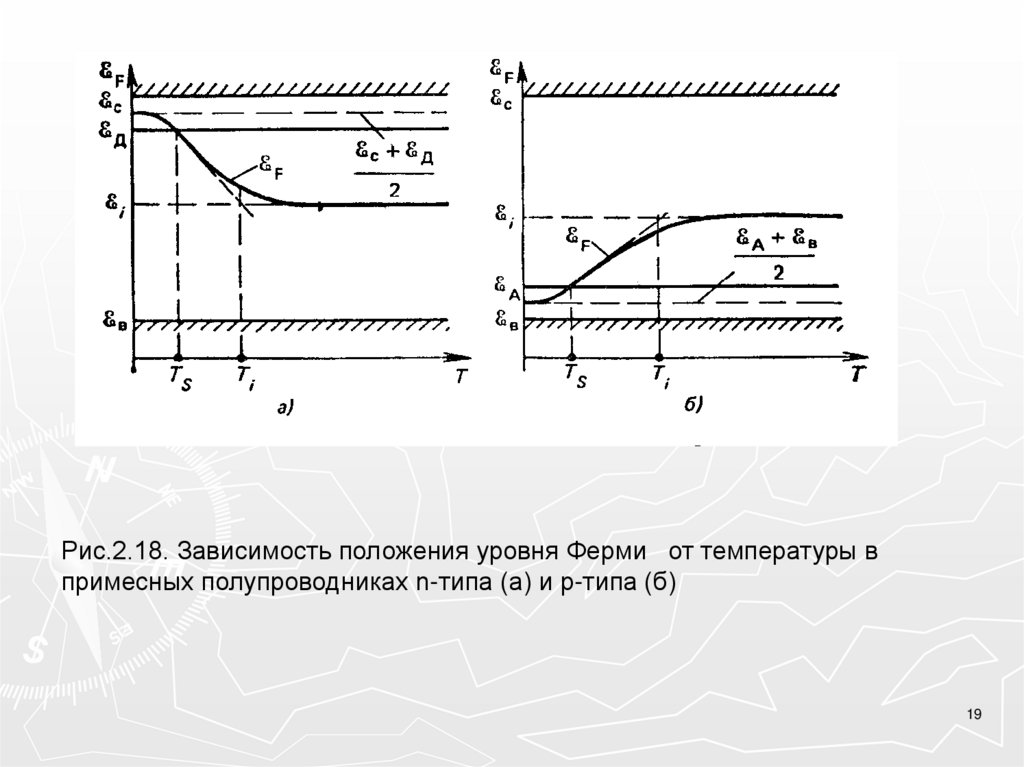
Рис.2.18. Зависимость положения уровня Ферми от температуры в
примесных полупроводниках n-типа (а) и p-типа (б)
19

20.

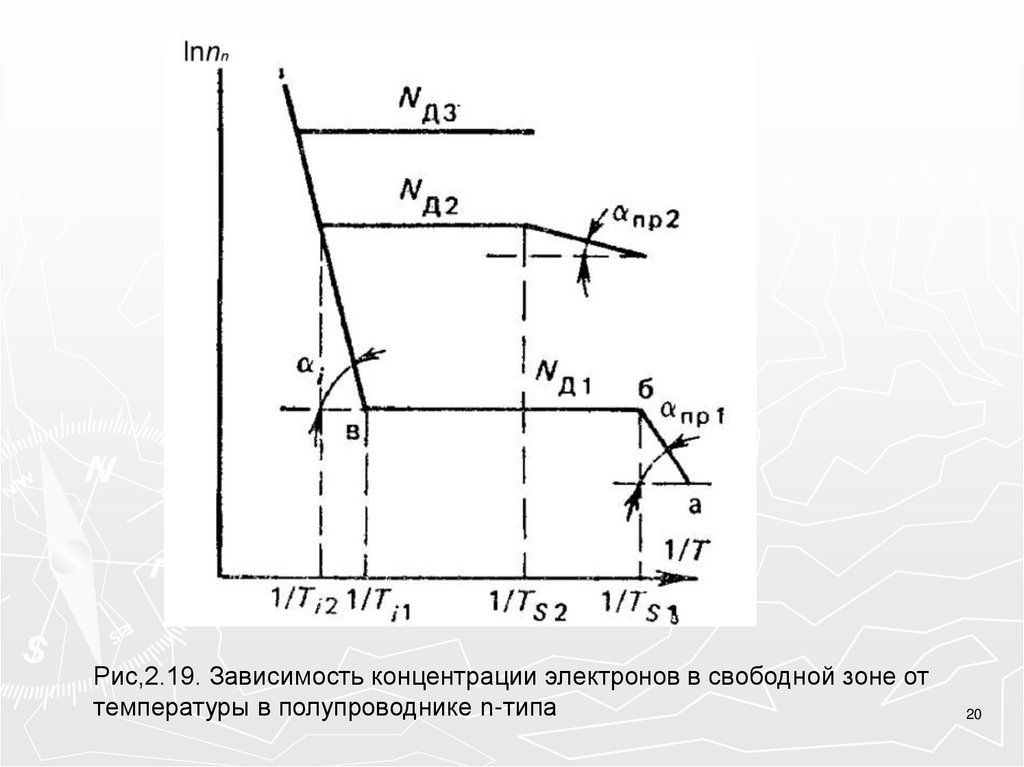
Рис,2.19. Зависимость концентрации электронов в свободной зоне от
температуры в полупроводнике n-типа
20

21.

На рис. 2.19 приведена температурная зависимость концентрации электронов в
зоне проводимости для полупроводника n-типа.
На кривой имеются три характерных участка:
аб –примесной электропроводности,
бв –области истощения примеси
вг –собственной электропроводности.
Положение уровня Ферми и концентрация носителей заряда в полупроводниках ртипа определяются так же, как и для полупроводников n-типа.
Если известны концентрации основных носителей заряда, то можно вычислить
концентрации неосновных носителей в примесных полупроводниках,
воспользовавшись соотношением
np nn pn n p p p ni
2
(2.43)
21

22.

где n, р, n n , p n , n p , p p
- концентрации электронов и дырок,
соответственно, в полупроводниках: собственном, n-типа и p-типа.
Отсюда находим концентрации неосновных носителей заряда:
2
ni
pn
nn
(2.44)
2
ni
np
pp
(2.45)
Рабочий температурный диапазон примесных полупроводников
ограничен снизу температурой полной ионизации примесей, а сверху критической температурой, при которой примесный полупроводник
превращается в собственный.
В рабочем диапазоне можно считать все примесные атомы полностью
ионизированными и пренебречь собственной концентрацией пi, положив
концентрации основных носителей заряда равными концентрациям примесных
атомов:
(2.46)
n =
Д
n
N
pp = N
A
(2.47)
22

23.

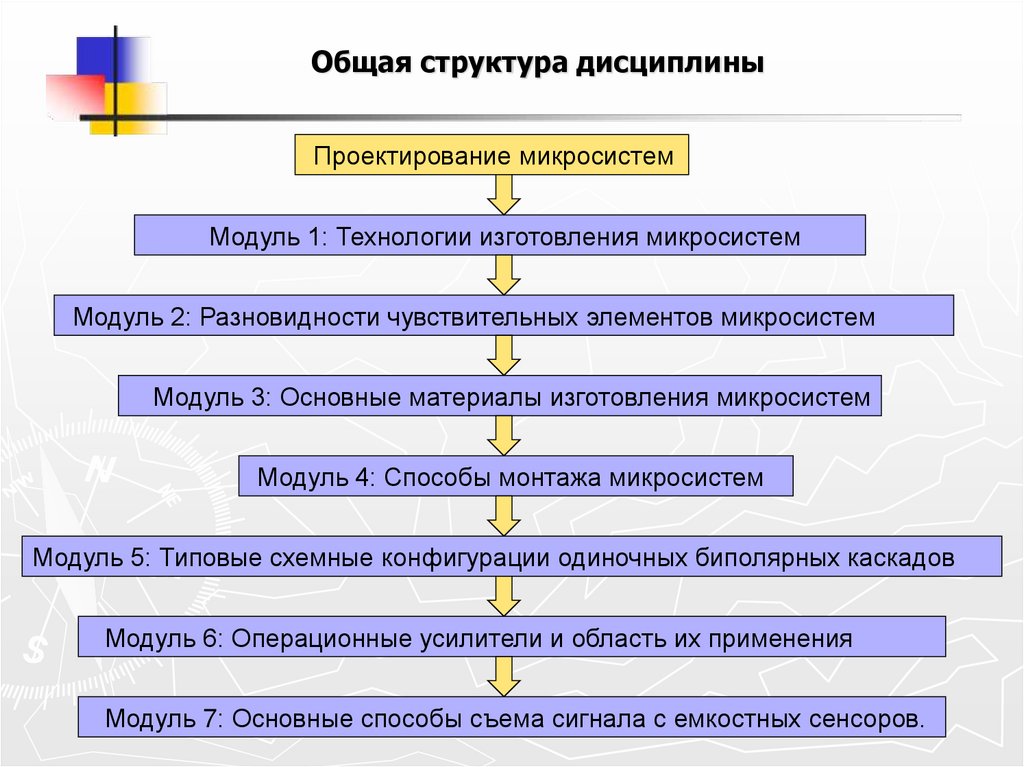
Общая структура дисциплины
Проектирование микросистем
Модуль 1: Технологии изготовления микросистем
Модуль 2: Разновидности чувствительных элементов микросистем
Модуль 3: Основные материалы изготовления микросистем
Модуль 4: Способы монтажа микросистем
Модуль 5: Типовые схемные конфигурации одиночных биполярных каскадов
Модуль 6: Операционные усилители и область их применения
Модуль 7: Основные способы съема сигнала с емкостных сенсоров.

24.

Модуль 1:Технологии изготовления микросистем
Состав модуля 1:
• объемная технология
• поверхностная технология
• соединение слоев внутри микросистемы
Модуль 2: Разновидности чувствительных элементов
микросистем
Состав модуля 2:
• пьезорезистивные чувствительные элементы
• емкостные чувствительные элементы
• пьезоэлектрические чувствительные элементы
• резонансные чувствительные элементы

25.

Модуль 3: Основные материалы изготовления микросистем
Состав модуля 3:
• металлы и способы их получения
• диэлектрики и способы их получения
• поликристаллический кремний и способы
его получения
Модуль 4: Способы монтажа микросистем
Состав модуля 4:
• роль корпусов в микросистемах
• разновидности корпусов
• монтаж микросистем на подложке
• многокристальные микросистемы
• интеграция микросистем с микроэлектронными схемами
• надежность и неисправность микросистем

26.

Модуль 5: Типовые схемные конфигурации одиночных
биполярных каскадов
Состав модуля 5:
• схема с общим эмиттером, способы стабилизации
• схема с общей базой, схема с общим коллектором
• токовые зеркала
• дифференциальный каскад
Модуль 6: Операционные усилители и область их применения
Состав модуля 6:
• Классификация ОУ, простейшие схемы
• Выполнение арифметических преобразований
с помощью ОУ
• Внешняя и внутренняя компенсация ОУ
• Усилители Нортона
• Генераторы на ОУ
• Активные фильтры
26

27.

Модуль 7: Основные способы съема сигнала с емкостных
сенсоров
Состав модуля 7:
• компенсационная схема акселерометра
с токовым выходом
• компенсационная схема акселерометра
с разделением выходов
• компенсационная схема акселерометра
с амплитудной модуляцией
• компенсационная схема акселерометра
с автоматическим выбором разрешающей
способности
• мостовая схема акселерометра
• компенсационная схема акселерометра
с обратной связью по напряжению
27