Лекция_2_формулы_10.09.2024

1. Лекция №2 Разработка программного обеспечения для моделирования физических процессов

Санкт-Петербургский политехнический университет Петра Великого
Лекция №2
Разработка программного обеспечения
для моделирования физических
процессов
Воскобойников С.П.
Доцент ВШ ПИ ИКНК, к.ф.-м.н.
voskob_sp@spbstu.ru
10.09.2024

2. Содержание

• Численное решение краевых задач для ОДУ
второго порядка
• Постановка задачи. Типы краевых условий.
• Метод конечных разностей.
• Интегро-интерполяционный метод (метод
баланса)
• Метод прогонки

3. Постановка краевой задачи для ОДУ второго порядка

d 2u x
du x
p x
r
x
q x u x f x ,
2
dx
dx
0 C1 p x C2 , x a, b
Краевые условия первого рода
u x x a 1 ,
u x x b 2
Краевые условия третьего рода
du x
du x
1u x x a 1 ,
2u x x b 2 ,
dx x a
dx x b
1 0,
2 0
Краевые условия второго рода как частный случай условий третьего рода
1 0,
2 0
du x
1 ,
dx x a
du x
2
dx x b

4. Постановка краевой задачи для ОДУ второго порядка

Краевые условия первого рода как частный случай условий третьего рода
du x
du x
1u x x a 1* ,
2u x x b 2* ,
dx x a
dx x b
1 0,
2 0
1* 1 1, 2* 2 2
du x
1u x x a 1 1 ,
dx x a
1 du x
u x x a 1 ,
1 dx x a
1 ,
0 u x x a 1 ,
du x
2u x x b 2 2 ,
dx x b
1 du x
u x x b 2 ,
2 dx x b
2
0 u x x b 2 ,

5. Метод конечных разностей (МКР)

N число разбиений интервала a, b
Неравномерная сетка x0 x1 ... xN , xi a, b , x0 a, xN b
hi xi xi 1 , i 1,2,..., N
Равномерная сетка hi h, h
ui u xi
u 2ui ui 1
d 2u x
i 1
,
2
dx x x
h2
i
vi v xi
b a
, xi a ih, i 0,1,..., N
N
vi ui
du x
u u
i 1 i 1 ,
dx x xi
2h
u u
du x
i i 1 ,
dx x xi
h
du x
u u
i 1 i ,
dx x xi
h

6. Метод конечных разностей (МКР) Пример разностной схемы с граничными условиями первого рода

d 2u x
du x
p x
r
x
q x u x f x ,
2
dx
dx
Краевые условия первого рода
u x x a 1 ,
0 C1 p x C2 , x a, b
u x x b 2
u x x x 1 ,
i 0
i
d 2u x
du x
p
x
r
x
q
x
u
x
f x x x , i 1,2,..., N 1
2
i
dx
dx
x xi
u x x x 1,
i N
N
vi 1,
pi
i 0
vi 1 2vi vi 1
vi 1 vi 1
r
qi vi f i , i 1,2,..., N 1
i
2
h
2h
vi 2 ,
i N

7. Метод конечных разностей (МКР) Пример разностной схемы с граничными условиями первого рода

vi 1,
i 0
r
pi ri
2p
p
2 vi 1 2 i qi vi 2i i vi 1 fi , i 1,2,..., N 1
2h
2h
h
h
h
vi 2 ,
i N
c0 1, b0 0
r
p
p
ai 2i i , ci 2i qi ,
2h
h
h
r
p
bi 2i i , i 1,2,..., N 1
2h
h
aN 0, cN 1
ci vi bi vi 1 fi , i 0
ai vi 1 ci vi bi vi 1 f i ,
ai vi 1 ci vi
fi ,
i 1,2,..., N 1
i N

8. Метод конечных разностей (МКР) Пример разностной схемы с граничными условиями первого рода

Av f ,
c0
a
1
A
b0
c1
.
A N 1 N 1 , v, f R( N 1)
b1
.
.
.
.
.
.
.
.
aN 1
cN 1
aN
,
bN 1
cN
v0
v
1
.
v . ,
.
v N 1
v
N
f0
f
1
.
f .
.
f N 1
f
N

9. Метод конечных разностей (МКР) Пример разностной схемы с граничными условиями третьего рода

d 2u x
du x
p x
r
x
q x u x f x ,
dx 2
dx
0 C1 p x C2 , x a, b
Краевые условия третьего рода
du x
1u x x a 1 ,
dx x a
du x
2u x x b 2 ,
dx x b
vi 1 vi 1
1vi 1 ,
2h
pi
vi 1 2vi vi 1
vi 1 vi 1
r
qi vi f i ,
i
2
h
2h
vi 1 vi 1
2 vi 2 ,
2h
v 1 v x 1 ,
x 1 a h
1 0,
2 0
i 0
i 0,1,2,..., N
i N
vN 1 v xN 1 ,
xN 1 b h

10. Метод конечных разностей (МКР) Пример разностной схемы с граничными условиями третьего рода

vi 1 vi 1
1vi 1 ,
2h
vi 1 vi 1 2h 1vi 1 ,
i 0
vi 1 2vi vi 1
vi 1 vi 1
r
qi vi fi , i 0
i
h2
2h
q
p
f r
p
p r
2i 1 i 1 i vi 2i vi 1 i i 1 i 1 ,
h 2
2
h
2 2
h
h
i 0
pi
v v
i 1 i 1 2 vi 2 ,
2h
pi
i N
vi 1 2vi vi 1
vi 1 vi 1
r
qi vi fi ,
i
h2
2h
i 0
vi 1 vi 1 2h 2vi 2 ,
i N
i N
pi
qi
f i ri
pi
pi 2 ri
v
v
2,
i
1
2
i
2
2
2
h
h 2
2
2 2
h
h
i N
r
pi ri
2p
p
2 vi 1 2 i qi vi 2i i vi 1 fi , i 1,2,..., N 1
2h
2h
h
h
h

11. Интегро-интерполяционный метод (метод баланса)

d
du x
k x
q x u x f x ,
dx
dx
Краевые условия первого рода
0 C1 k x C2 ,
u x x a 1 ,
x a, b
u x x b 2
Краевые условия второго рода 1 0, 2 0
k ( x)
du x
1 ,
dx x a
k ( x)
du x
2
dx x b
Краевые условия третьего рода
k x
du x
1u x x a 1 ,
dx x a
k x
du x
2u x x a 2 ,
dx x a
1 0,
2 0
не рекомендуе тся раскрывать скобки
d 2u x dk x du x
k x
q
x
u
f x ,
2
dx
dx dx
p x k x , r x
dk x
dx

12. Интегро-интерполяционный метод (метод баланса)

d
du x
k x
q x u x f x ,
dx
dx
0 C1 k x C2 ,
N число разбиений интервала a, b
x0 x1 ... xN ,
xi a, b ,
x0 a, xN b
hi xi xi 1 , i 1,2,..., N
xi 1/ 2
xi xi 1
,
2
i 1,2,..., N
hi 1
i 0
2 ,
h hi 1
i i
, i 1,2,..., N 1
2
hi
i N
2 ,
x a, b

13. Интегро-интерполяционный метод (метод баланса) Пример разностной схемы с граничными условиями первого рода

d
du
k x q x u f x ,
dx
dx
0 C1 k x C2 ,
i 1 / 2
d
du
k x q x u dx f x dx,
dx
dx
xi 1 / 2
xi 1 / 2
xi 1 / 2
x a, b
x
i 1,2,..., N 1
xi 1/ 2
xi 1/ 2
du
du
k x
k x
qudx fdx,
dx x xi 1/ 2
dx x xi 1/ 2 xi 1/ 2
xi 1/ 2
u u
u u
du
i i 1 i i 1
h
dx x xi 1 / 2
hi
2 i
2
vi 1 ,
xi 1 / 2
x dx ,
i
xi 1 / 2
i 0
v v
v v
ki 1/ 2 i 1 i ki 1/ 2 i i 1 i qi vi i f i , i 1,2,..., N 1
hi 1
hi
vi 2 ,
i N
i

14. Интегро-интерполяционный метод (метод баланса) Пример разностной схемы с граничными условиями первого рода

c0 1, b0 0, g0 1
k
ai i 1/ 2 ,
hi
ci
ki 1/ 2 ki 1/ 2
i qi ,
hi
hi 1
Av g ,
b0
c1
.
i 1,2,..., N 1
gN 2
aN 0, cN 1,
c0
a
1
A
k
bi i 1/ 2 , g i i f i ,
hi 1
A N 1 N 1 , v, g R( N 1)
b1
.
.
.
.
.
.
.
.
a N 1
cN 1
aN
A AT
,
bN 1
cN
v0
v
1
.
v . ,
.
v
N 1
v
N
g0
g
1
.
g .
.
g
N 1
g
N

15. Симметричная разностная схема с граничными условиями I рода

vi 1,
v v
v
ki 1 / 2 i 1 i ki 1 / 2 i i qi vi i fi ki 1 / 2 1 ,
hi 1
hi
hi
i 0
i 1
v v
v v
ki 1 / 2 i 1 i ki 1 / 2 i i 1 i qi vi i fi , i 2,..., N 2
hi 1
hi
v
v v
ki 1 / 2 i ki 1 / 2 i i 1 i qi vi i fi ki 1 / 2 2 , i N 1
hi 1
hi
hi 1
vi 2 ,
i N

16. Симметричная разностная схема с граничными условиями I рода

c0 1,
ci
b0 0,
ki 1 / 2 ki 1 / 2
i qi ,
hi
hi 1
k
k
k
ai i 1 / 2 , ci i 1 / 2 i 1 / 2 i qi ,
hi
hi
hi 1
k
k
k
ai i 1 / 2 , ci i 1 / 2 i 1 / 2 i qi ,
hi
hi
hi 1
aN 0,
k
bi i 1 / 2 , gi i f i ki 1 / 2 1 ,
hi 1
hi i
k
bi i 1 / 2 , g i i f i ,
hi 1
i 1
i 2,..., N 2
gi i f i ki 1 / 2
2
hi 1 i
,
i N 1
gN 2
cN 1,
Av g ,
g0 1
A N 1 N 1 , v, g R( N 1)
A AT

17. Интегро-интерполяционный метод (метод баланса)

Краевое условие третьего рода
k x
du x
1u x x a 1 ,
dx x a
1 0,
i 1 / 2
d
du
k x q x u dx f x dx,
dx
dx
xi
xi
x i 1 / 2
x
i 0
xi 1 / 2
xi 1 / 2
du
du
k x
k x
qudx fdx,
dx
dx
x xi 1 / 2
x xi
xi
xi
u u
u u
du
k x
k xi 1/ 2 i 1 i ki 1/ 2 i 1 i ,
h
dx x xi 1 / 2
hi 1
2 i 1
2
k x
i 0
xi 1 / 2
x dx ,
i
i
xi
du x
1u x x x 1 , i 0
i
dx x xi
v v
ki 1/ 2 i 1 i 1vi 1 i qi vi i f i , i 0
hi 1

18. Интегро-интерполяционный метод (метод баланса)

Краевое условие третьего рода
k x
du x
2u x x b 2 ,
dx x b
2 0
i
d
du
k x q x u dx f x dx,
dx
dx
xi 1 / 2
xi 1 / 2
xi
x
i N
xi
xi
du
du
k x
k x
qudx fdx,
dx x xi
dx x xi 1 / 2 xi 1 / 2
xi 1 / 2
du
u ui 1
u ui 1
k x
k xi 1 / 2 i
ki 1 / 2 i
,
hi
dx x xi 1/ 2
h
i
2
2
k ( x)
i N
xi
x dx ,
i
x i 1 / 2
du x
2u x x x 2 , i N
i
dx x xi
vi vi 1
2vi 2 ki 1 / 2
i qi vi i fi , i N
h
i
i

19. Интегро-интерполяционный метод (метод баланса) Пример разностной схемы с граничными условиями третьего рода

v v
ki 1/ 2 i 1 i 1vi 1 i qi vi i f i , i 0
hi 1
v v
v v
ki 1/ 2 i 1 i ki 1/ 2 i i 1 i qi vi i f i , i 1,2,..., N 1
hi 1
hi
v v
2vi 2 ki 1/ 2 i i 1 i qi vi i f i , i N
hi
ci vi bi vi 1 fi , i 0
ai vi 1 ci vi bi vi 1 f i ,
i 1,2,..., N 1
ai vi 1 ci vi
i N
fi ,

20. Интегро-интерполяционный метод (метод баланса) Пример разностной схемы с граничными условиями третьего рода

ci
ki 1/ 2
i qi 1 ,
hi 1
k
bi i 1/ 2 , g i f i 1 ,
hi 1
k
k
k
ai i 1 / 2 , ci i 1 / 2 i 1 / 2 i qi ,
hi
hi
hi 1
k
ai i 1/ 2 ,
hi
ci
ki 1/ 2
i qi 2 ,
hi
b0
c1
.
g i f i 2 ,
b1
.
.
i 1,2,..., N 1
i N
A N 1 N 1 , v, g R( N 1)
Av g ,
c0
a
1
A
k
bi i 1 / 2 , g i f i ,
hi 1
i 0
.
.
.
.
.
.
a N 1
cN 1
aN
,
bN 1
cN
A AT
v0
v
1
.
v . ,
.
v
N 1
v
N
g0
g
1
.
g .
.
g
N 1
g
N

21. Интегро-интерполяционный метод (метод баланса)

1 d n
du r
n
r k r
q r u r f r ,
dr
r dr
0 C1 k r C2 ,
n 1 одномерный случай цилиндрическая системы координат
n 2 одномерный случай сферической системы координат
u r 0 ограничено
Краевые условия первого рода
u r r R
Краевое условие второго рода
k r
du r
,
dr r R
0
Краевое условие третьего рода
k r
du r
u r r R ,
dr r R
0
r 0, R

22. Интегро-интерполяционный метод (метод баланса)

1 d n
du r
n
r k r
q r u r f r ,
dr
r dr
0 C1 k r C2 ,
N число разбиений интервала 0, R
r0 r1 ... rN , ri 0, R , r0 0, rN R
hi ri ri 1 , i 1,2,..., N
r r
ri 1 / 2 i i 1 ,
2
i 1,2,..., N
hi 1
i 0
2 ,
h h
i i i 1 , i 1,2,..., N 1
2
hi
i N
2 ,
r 0, R

23. Интегро-интерполяционный метод (метод баланса) Аппроксимация уравнения

1 d n
du r
n
r k r
q r u r f r ,
dr
r dr
0 C1 k r C2 ,
i 1 / 2
d n
du r n
n
r k r
r q r u r dr r f r dr ,
dr
dr
ri 1 / 2
ri 1 / 2
ri 1 / 2
r 0, R
r
i 1,2,..., N 1
ri 1 / 2
n
ri 1 / 2 n
du r
du r
n
n
r k r
r k r
r q r u r dr r f r dr ,
dr
dr
r ri 1 / 2
r ri 1 / 2
ri 1 / 2
ri 1 / 2
du r
u ui 1 ui ui 1
i
hi
dr r ri 1/ 2
hi
2
2
r
i 1 / 2
n
n
r
r
dr
r
i ,
i
i
ri 1 / 2
v v
v v
ri n 1/ 2 ki 1/ 2 i 1 i ri n 1/ 2 ki 1/ 2 i i 1 i ri n qi vi i ri n f i ,
hi 1
hi
i 1,2,..., N 1

24. Интегро-интерполяционный метод (метод баланса) Условие ограниченности

1 d n
du r
0 C1 k r C2 ,
n
r
k
r
q
r
u
r
f r ,
dr
r dr
du r
nk
r
d
du r
dr
k r
q
r
u
r
f r
dr
r
dr
du r
nk r
du r
0
dr
k
r
0
lim
dr r 0
0
r
r 0
du r
dr n d k r du r
r
dr
dr
nk r
lim
r 0
d
du r
n 1 k r
q
r
u
r
f r r 0
dr
dr
r 0
du r
u r 0 ограничено k r
0
dr r 0
r 0, R

25. Интегро-интерполяционный метод (метод баланса) Аппроксимация условия ограниченности

1 d n
du r
n
r
k
r
q
r
u
r
f r ,
dr
r dr
i 1 / 2
d n
du r n
n
r k r
r q r u r dr r f r dr ,
dr
dr
ri
ri
ri 1 / 2
r 0, R
0 C1 k r C2 ,
r
i 0
ri 1 / 2
n
ri 1 / 2 n
du r
du r
n
n
r k r
r k r
r q r u r dr r f r dr ,
dr r ri 1 / 2
dr r ri
ri
ri
i 0
du r
u u u u
i 1 i i 1 i
h
dr r ri 1/ 2
hi 1
2 i 1
2
r ri 1 / 2
r n 1
n
n
r r r dr ri r r dx i n 1
r r
i
i
ri 1 / 2
ri 1 / 2
ri n 1 / 2
i i
,
n 1
i
n
vi 1 vi
ri n 1/ 2
ri n 1/ 2
ri 1 / 2 k i 1 / 2
0 i qi vi
i fi
,
hi 1
n 1
n 1
i 0

26. Интегро-интерполяционный метод (метод баланса) Аппроксимация условия третьего рода

1 d n
du r
0 C1 k r C2 ,
n
r
k
r
q
r
u
r
f r ,
dr
r dr
du r
Краевое условие третьего рода : k r
u r r R ,
dr r R
i
d n
du r n
n
r k r
r q r u r dr r f r dr ,
dr
dr
ri 1 / 2
ri 1 / 2
ri
,
r 0, R
0
r
i N
ri
ri
n
du r
du
r
r k r
r n k r
r n q r u r dr r n f r dr ,
dr r ri
dr r ri 1 / 2 ri 1 / 2
ri 1 / 2
u u
u u
du r
i i 1 i i 1
h
dr r ri 1 / 2
hi
2 i
2
r
du r
k r
u r r r , i N
i
dr r ri
i
n
n
r
r
dr
r
i i i ,
ri 1 / 2
v v
ri n vi ri n 1 / 2ki 1 / 2 i i 1 i ri n qi vi i ri n fi , i N
hi

27. Интегро-интерполяционный метод (метод баланса) Пример разностной схемы в криволинейных координатах

1 d n
du r
n
r
k
r
q
r
u
r
f r ,
dr
r dr
u r 0 ограничено k r
r 0, R
du r
u r r R ,
dr r R
0
du r
0
dr r 0
Краевое условие третьего рода : k r
,
0 C1 k r C2 ,
n
vi 1 vi
ri n 1/ 2
ri n 1/ 2
ri 1 / 2 k i 1 / 2
0 i qi vi
i fi n 1 ,
h
n
1
i 1
n
vi 1 vi
vi vi 1
n
n
ri 1/ 2 ki 1/ 2
ri 1/ 2 ki 1/ 2
i ri qi vi i ri n f i ,
hi 1
hi
i 0
i 1,2,..., N 1
n
vi vi 1
n
n
ri vi ri 1 / 2ki 1 / 2
i ri qi vi i ri n fi , i N
hi

28. Разностная схема в криволинейных координатах с граничными условиями III рода

ci ri n 1 / 2
ki 1 / 2
1
i ri n 1 / 2 qi ,
hi 1 n 1
bi ri n 1 / 2
bi rin 1 / 2
ki 1/ 2
,
hi
ci rin 1 / 2
ki 1/ 2
k
rin 1 / 2 i 1/ 2 i ri n qi ,
hi
hi 1
ai rin 1 / 2
ki 1/ 2
,
hi
ci rin 1 / 2
ai rin 1 / 2
c0
a
1
A
b0
c1
.
1
i ri n 1 / 2 f i ,
n 1
i 0
i 1,2,..., N 1
g i ri n f i ri n ,
i N
A N 1 N 1 , v, g R( N 1)
b1
.
.
gi
ki 1/ 2
, g i i ri n f i ,
hi 1
ki 1/ 2
i ri n qi ri n ,
hi
Av g ,
,
ki 1 / 2
,
hi
.
.
.
.
.
.
a N 1
cN 1
aN
v0
v
1
.
v . ,
.
v
N 1
v
N
,
bN 1
cN
A AT
g0
g
1
.
g .
.
g
N 1
g
N

29. Уравнение в криволинейных координатах без особенности в нуле

1 d
du r
n r n k r
q
r
u
r
f r ,
dr
r dr
r RL , RR
RL 0
0 C1 k r C2 ,
n 1 одномерный случай цилиндрическая системы координат
n 2 одномерный случай сферической системы координат
Краевые условия первого рода
u r r R 1 ,
,
L
u r
r RR
2
Краевые условия второго рода
k r
du r
1 ,
dr r RL
k r
du r
2 ,
dr r RR
Краевые условия третьего рода
k r
du r
2u r r R 1 ,
L
dr r RL
1 0,
k r
du r
dr
2u r r R 2 ,
R
r RR
2 0

30. Интегро-интерполяционный метод (метод баланса) Аппроксимация условия третьего рода слева

i 1 / 2
d n
du r n
n
r k r
r q r u r dr r f r dr ,
dr
dr
ri
ri
ri 1 / 2
r
i 0
ri 1 / 2
n
ri 1 / 2 n
du r
du r
n
n
r k r
r k r
r q r u r dr r f r dr ,
dr r ri 1 / 2
dr r ri
ri
ri
,
,
u u u u
du r
i 1 i i 1 i
h
dr r ri 1 / 2
hi 1
2 i 1
2
k r
du r
1u r r R 1
L
dr r RL
v v
ri n 1/ 2 ki 1/ 2 i 1 i ri n 1u r r R 1 i ri n qi vi i ri n f i ,
L
hi 1
i 0

31. Интегро-интерполяционный метод (метод баланса) Формальный подход

1 d n
du r
n
r k r
q r u r f r ,
dr
r dr
~
k r r n k r
~
f r r n f r
q~ r r n q r
d ~ du r ~ ~
k r
q r f r ,
dr
dr
k r
du r
1u r r R 1
L
dr r RL
r n k r
du r
r n 1u r r R r n
1
r
R
L
L
dr r RL
~1 r n 1
~1 r n 1
~ du r
k r
~1u r r R ~1
L
dr r RL
~2 r n 2
~2 r n 2
~ du r
k r
~2u r r R ~2
L
dr r RL

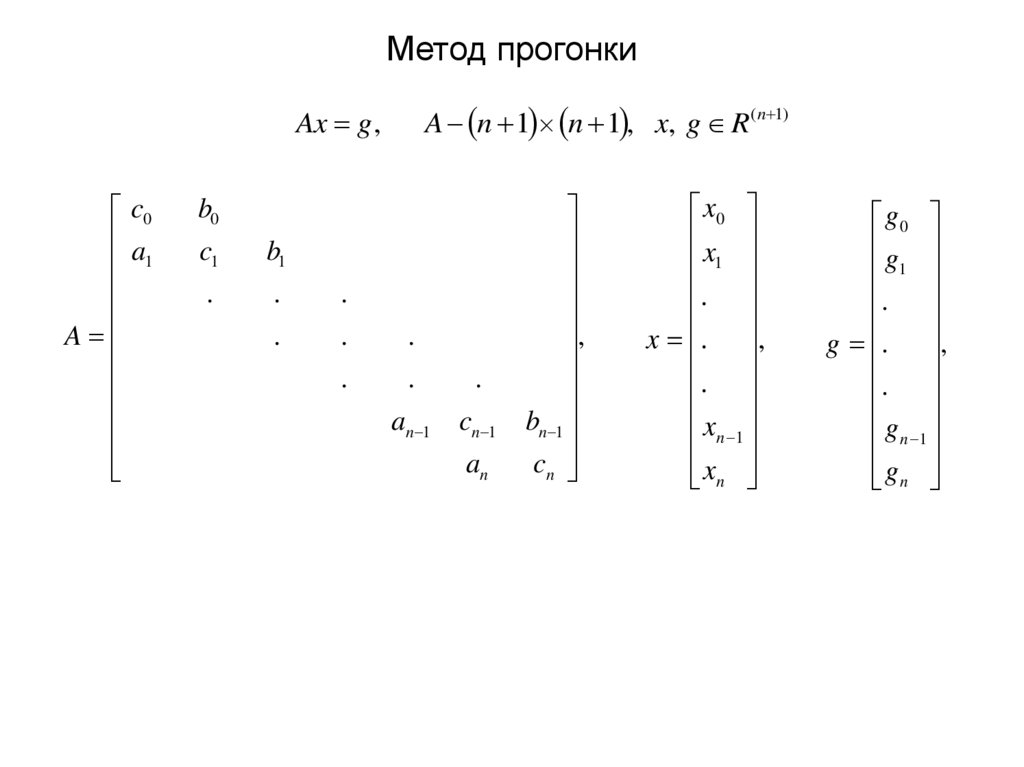
32. Метод прогонки

A n 1 n 1 , x, g R ( n 1)
Ax g ,
c0
a
1
A
b0
c1
.
b1
.
.
.
.
.
.
.
.
an 1
cn 1
an
,
bn 1
cn
x0
x
1
.
x . ,
.
xn 1
x
n
g0
g
1
.
g . ,
.
g
n 1
g
n

33. Метод прогонки

gi ,
ci xi bi xi 1
ai xi 1 ci xi bi xi 1 gi ,
a x c x
gi ,
i i 1 i i
i 0
ci ai bi
i 1,2, , n 1
i n
xi i 1 xi 1 i 1 ,
i 0,1,2,...., n 1
i и i свободные параметры (прогоночные коэффициен ты),
b
g
xi i xi 1 i ,
ci
ci
i 0
b
ci
i 1 i ,
xi 1 i xi i ,
i 1,2, , n 1
ai i ci xi bi xi 1 gi ai i ,
bi
g ai i
xi 1 i
,
a
c
a
c
i i
i
i i
i
i 1
i 1
bi
,
ai i ci
gi
,
ci
i 1,2,...., n 1
ai i xi i ci xi bi xi 1 gi ,
xi
i 1
i 1,2, , n 1
i 1,2, , n 1
i 1
i 1
g i ai i
,
ai i ci
i 1,2, , n 1
i 0

34. Метод прогонки

gi ,
ci xi bi xi 1
ai xi 1 ci xi bi xi 1 gi ,
a x c x
gi ,
i i 1 i i
i 0
ci ai bi
i 1,2, , n 1
i n
xi 1 i xi i ,
ai xi 1 ci xi
ai i xi i ci xi
xi
g i ai i
,
a
c
i i
i
b
c0
xn
1
gi ,
i n
i n 1, n 2,...,1,0
метод прогонки
g0
,
c0
g n an n
,
an n cn
i 1
i n
i n xi i 1 xi 1 i 1 ,
i 1
1 0 ,
gi ,
i 1
bi
,
ai i ci
i 1
xi i 1 xi 1 i 1 ,
ai i ci 0
g i ai i
,
ai i ci
i 1,2, , n 1
i n 1, n 2,...,1,0
~n