Лекция_17_Несобственные_интегралы_I_и_II_рода

1. Лекция 17. Несобственные интегралы I и II рода.

2.

Несобственные интегралы I-го рода
Несобственные интегралы являются обобщениями интегралов Римана.
Несобственные интегралы с бесконечными промежутками интегрирования (I-го
рода).
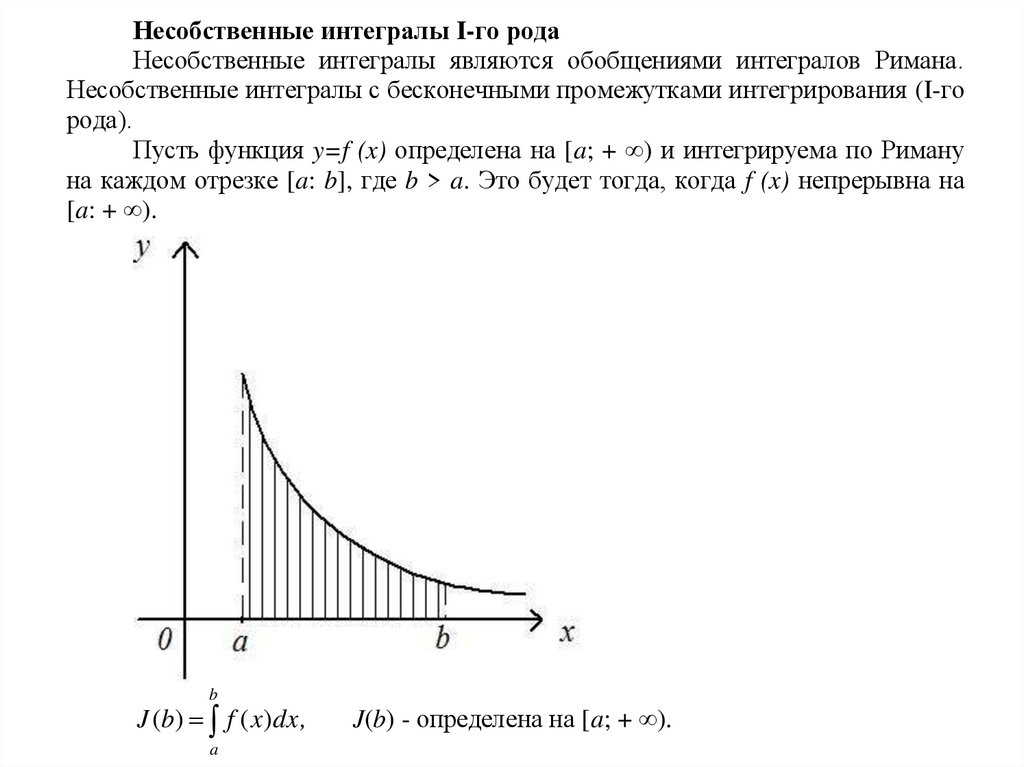
Пусть функция y=f (x) определена на [a; + ∞) и интегрируема по Риману
на каждом отрезке [a: b], где b > a. Это будет тогда, когда f (x) непрерывна на
[a: + ∞).
b
J (b) f ( x)dx ,
a
J(b) - определена на [a; + ∞).

3.

b
Df. 1 Если существует конечный предел: lim J (b) lim f ( x)dx , то этот
b
b
a
предел называется несобственным интегралом функции f(x) на [a; + ∞) и
обозначается: f ( x)dx
a
Df
b
f ( x)dx
f ( x)dx blim
a
a
Если указанный предел существует, то говорят, что несобственный
интеграл
b
a
a
f ( x)dx сходится. Если blim
f ( x)dx не является конечным числом,
или равен бесконечности, либо вовсе не существует, то говорят, что
f ( x)dx
a
расходится.
Пример: исследовать на сходимость:
b
dx
dx
1 b
1
1
1
lim
lim
(
)
lim
(
1
)
x 3 b x 3 b 2 x 2 1
2 b b 2
2
1
1
интеграл сходится.
-
несобственный

4.

b
b
dx
dx
ln x lim ln b - несобственный интеграл
x blim
blim
x
b
1
1
1
расходится.
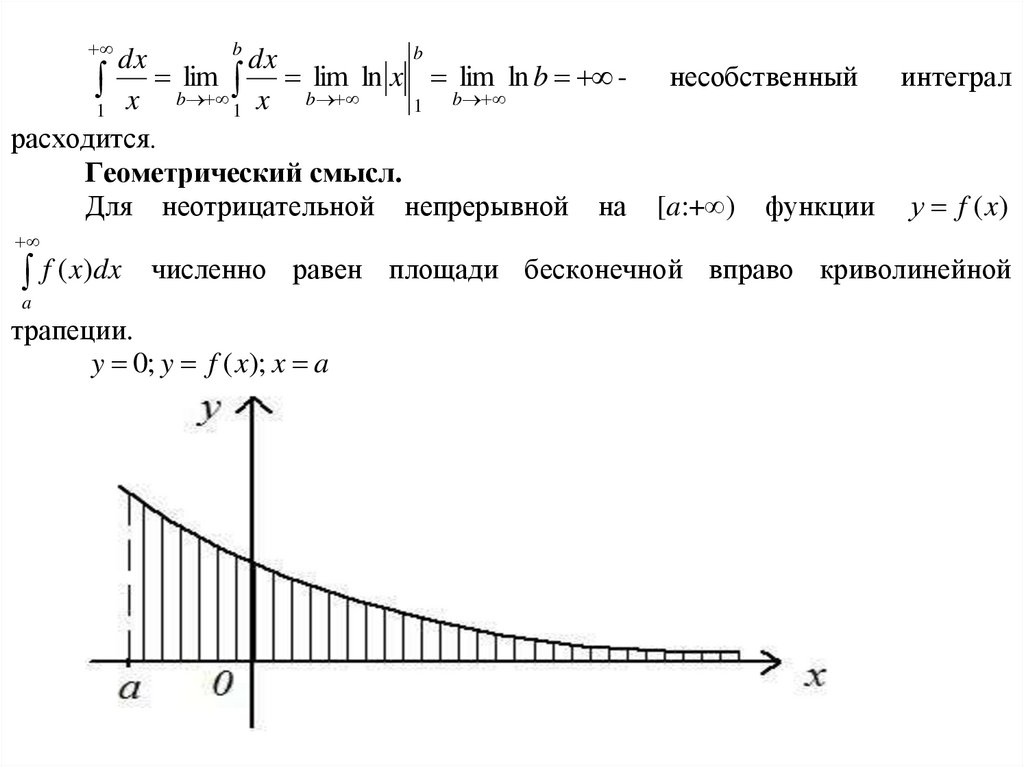
Геометрический смысл.
Для неотрицательной непрерывной на [a:+∞) функции у f (x)
f ( x)dx
численно равен площади бесконечной вправо криволинейной
a
трапеции.
y 0; y f ( x); x a

5.

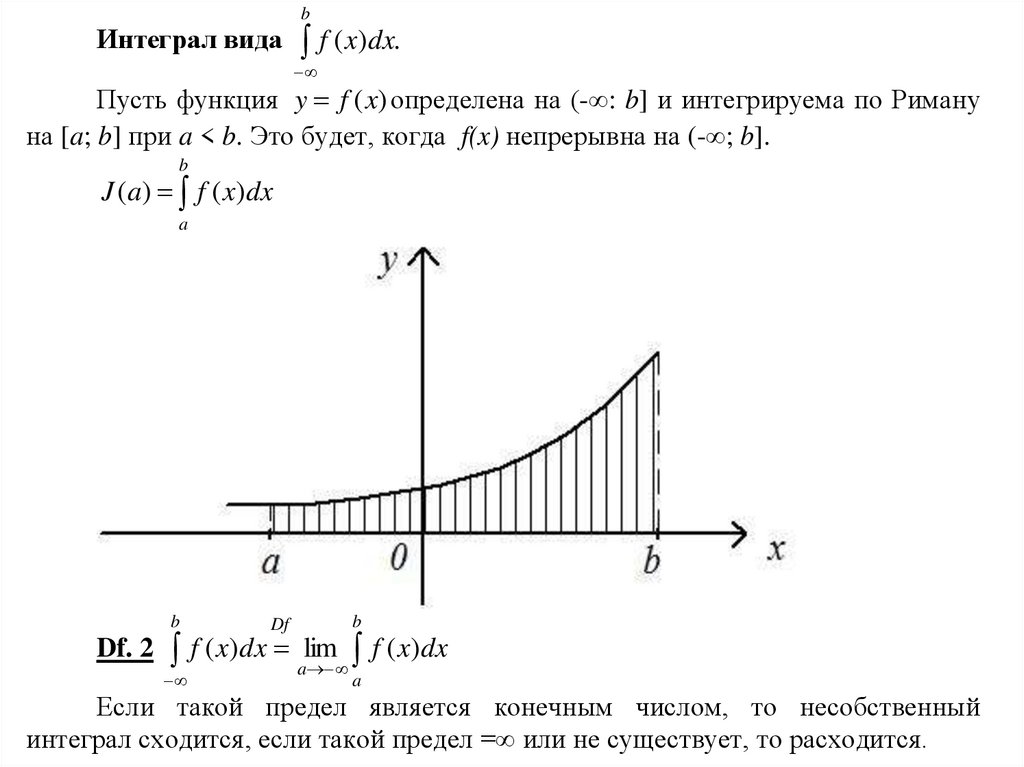
b
Интеграл вида f ( x)dx.
Пусть функция y f (x) определена на (-∞: b] и интегрируема по Риману
на [a; b] при a < b. Это будет, когда f(x) непрерывна на (-∞; b].
b
J (a) f ( x)dx
a
b
b
Df
Df. 2 f ( x)dx lim f ( x)dx
a
a
Если такой предел является конечным числом, то несобственный
интеграл сходится, если такой предел =∞ или не существует, то расходится.

6.

Геометрический смысл.
b
Для неотрицательной непрерывной функции
f ( x)dx численно равен
площади трапеции, неограниченной влево.
Пусть функция y=f(x) определена на (-∞:+∞) и интегрируема по Риману
на каждом [a; b] R, это будет, когда f(x) непрерывна на R.
Df c
c
Df. 3 f ( x)dx f ( x)dx f ( x)dx , где с R (c-любая точка).
f ( x)dx - сходится, если сходится каждый из интегралов в правой части
и расходится в противном случае.
Замечание. Df 3 корректно, то есть не зависит от точки с.

7.

dx
2
1 x
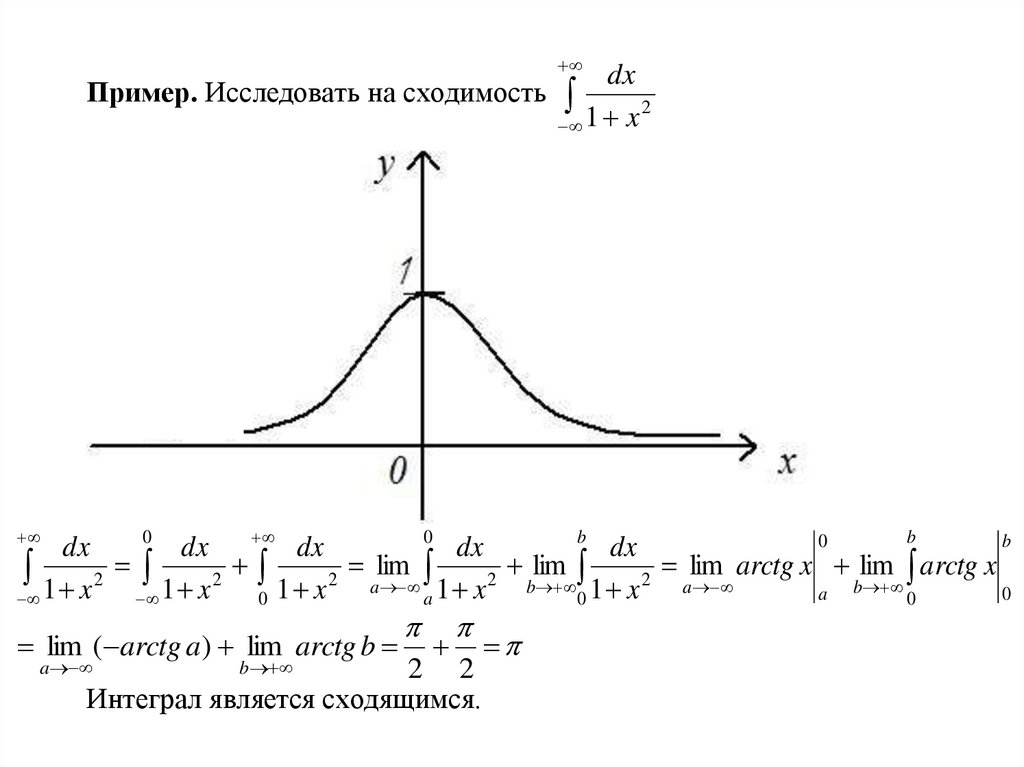
Пример. Исследовать на сходимость
0
0
b
b
0
b
dx
dx dx
dx
dx
lim
lim arctg x lim arctg x
1 x 2 1 x 2 1 x 2 alim
2
2
1 x
b 1 x
a
a b 0
0
0
a
0
lim ( arctg a) lim arctg b
a
b
2 2
Интеграл является сходящимся.

8.

Геометрическая интерпретация:
Для непрерывной и неотрицательной y=f(x) на (-∞: +∞) несобственный
интеграл численно равен неограниченной слева и справа трапеции.
Интегралы вида
a
b
объединяются под общим названием
несобственные интегралы первого рода.
Несобственные интегралы от неограниченных функций (II-го рода)
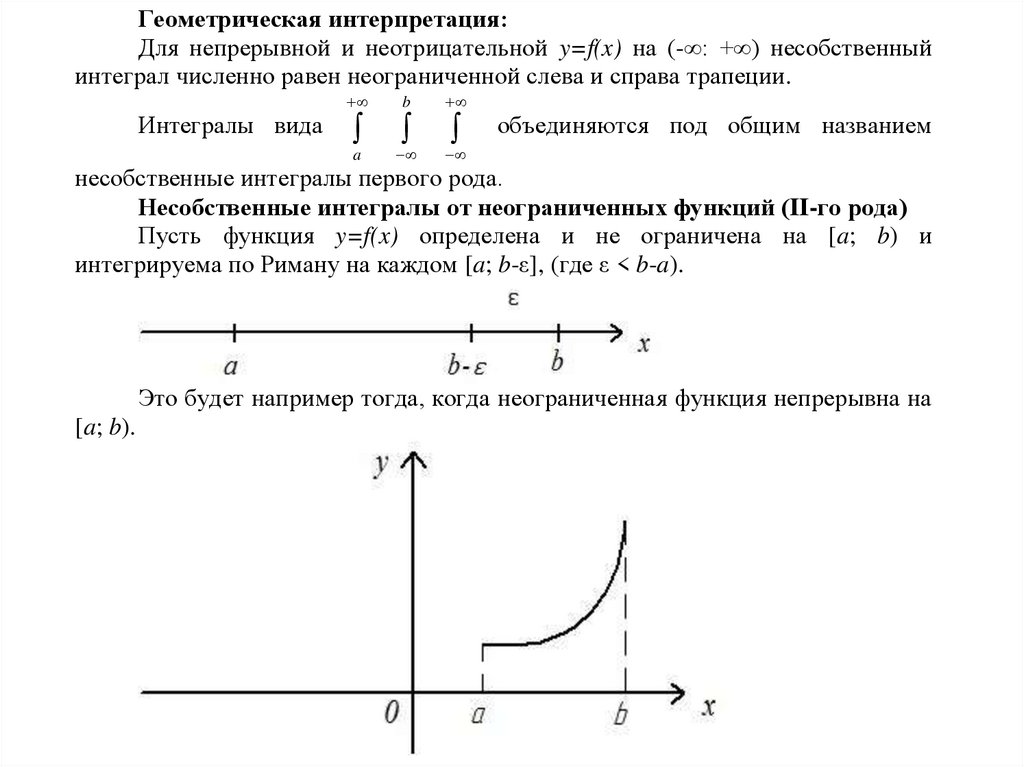
Пусть функция y=f(x) определена и не ограничена на [a; b) и
интегрируема по Риману на каждом [a; b-ε], (где ε < b-a).
Это будет например тогда, когда неограниченная функция непрерывна на
[a; b).

9.

b
b
Df
Df. 4 f ( x)dx lim f ( x)dx
a
0
a
Замечание 1. Обозначение такое же, как и у интеграла Римана. Если
указанный предел является конечным числом, то интеграл сходится, иначе
расходится.
Геометрическая интерпретация: Для непрерывной и неограниченной
f(x) численно представляет собой площадь неограниченной вверх
криволинейной трапеции.
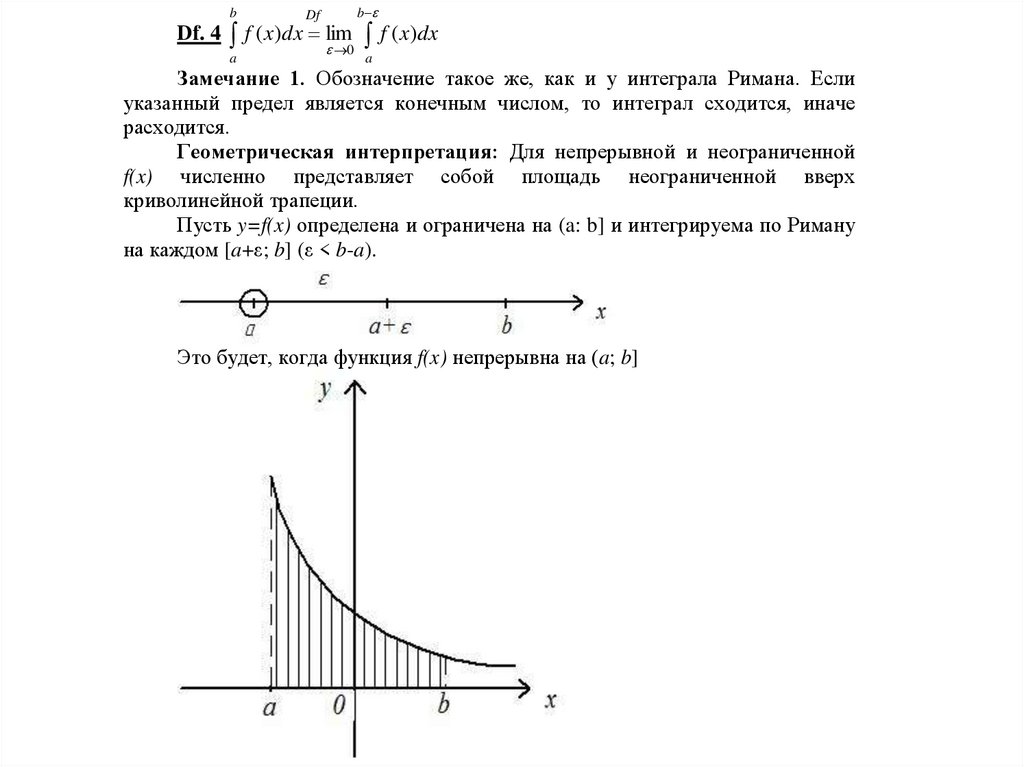
Пусть y=f(x) определена и ограничена на (a: b] и интегрируема по Риману
на каждом [a+ε; b] (ε < b-a).
Это будет, когда функция f(x) непрерывна на (a; b]

10.

b
Df. 5
b
Df
f ( x)dx lim
f ( x)dx . Если этот предел является конечным
0
a
a
числом, то сходится, иначе расходится.
Геометрическая интерпретация:
Для неотрицательных и непрерывных функций несобственный интеграл
численно равен площади неограниченной слева вверх трапеции.
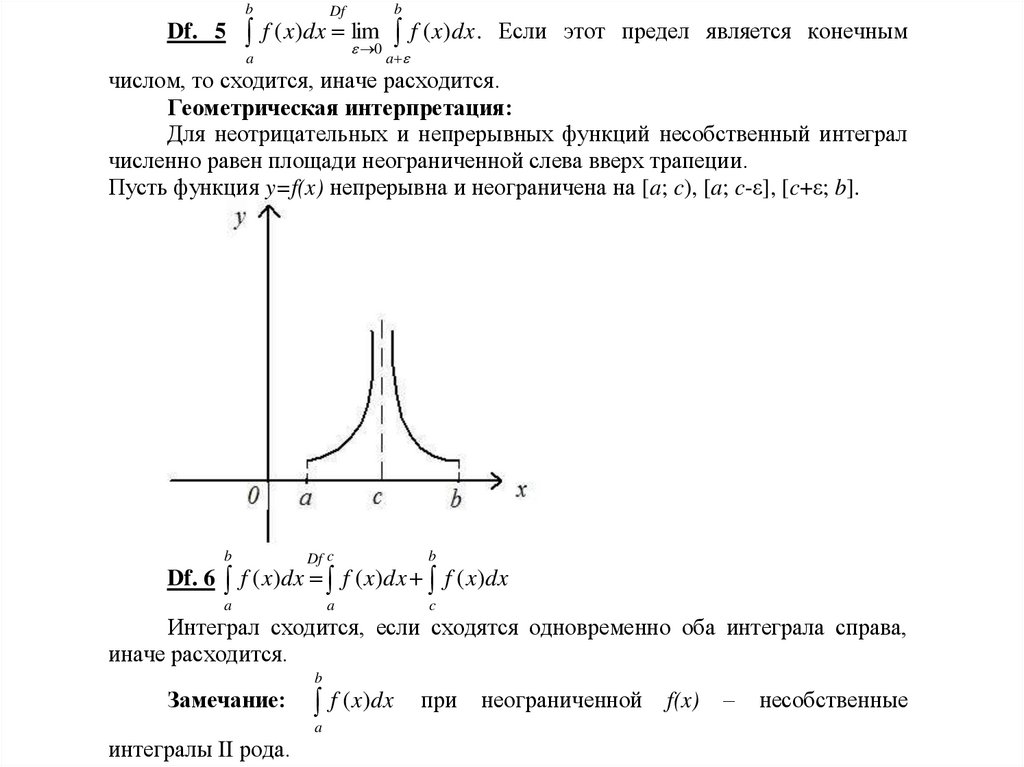
Пусть функция y=f(x) непрерывна и неограничена на [a; c), [a; c-ε], [c+ε; b].
b
Df c
b
a
a
c
Df. 6 f ( x)dx f ( x)dx f ( x)dx
Интеграл сходится, если сходятся одновременно оба интеграла справа,
иначе расходится.
b
Замечание:
f ( x)dx
a
интегралы II рода.
при
неограниченной
f(x)
–
несобственные