Похожие презентации:
1_5 СЛАУ_матр&крамер24
1.
Методы решения невырожденных СЛАУЕсли det A ≠ 0, СЛАУ может быть решена как матричное
уравнение (матричным методом) или с помощью
определителей (методом Крамера).
Опр. 7. СЛАУ, содержащая n уравнений с n неизвестными,
называется невырожденной, если ее матрица А невырождена,
т. е. det A ≠ 0.
Замечание. В невырожденной системе количество уравнений
равно количеству неизвестных.
2.
a11 x1 a12 x2a x a x
21 1 22 2
an1 x1 an 2 x2
a1n xn b1 ,
a2 n xn b2 ,
ann xn bn .
AX = B,
a11 a12
a
a22
21
где A
... ...
an1 an 2
(3)
(4)
... a1n
x1
b1
x
b
... a2 n
, X 2 , B 2 .
...
...
... ...
... ann
x
bn
n
3.
1. Матричный метод (метод обратной матрицы) решенияСЛАУ.
Если det A ≠ 0, решение уравнения (4), а значит, и
системы (3), может быть найдено по формуле
X = A–1B
AX B
A 1 AX A 1B EX A 1B
X A 1B.
4.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
x1
1
X = A–1B, где A 2 3 1 , X x2 , B 1 .
x
4
3 1 7
3
1 2 5
2 1
2 3
3 1
5
2
2 3 1 1
3 7
3 1
1 7
3 1 7
1 ( 21 1) 2 (14 3) 5 (2 9) 22 22 55 11 0,
5.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3 1
–22;
A11
1 7
6.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
1
–22;
7
1
–11;
7
7.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
1
–22;
7
1
–11;
7
2 3
A13
11;
3 1
8.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
1
2 5
–22; A21
–9;
7
1 7
1
–11;
7
2 3
A13
11;
3 1
9.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
1
2 5
–22; A21
–9;
7
1 7
1
1 5
–11; A22
–8;
7
3 7
2 3
A13
11;
3 1
10.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
1
2 5
–22; A21
–9;
7
1 7
1
1 5
–11; A22
–8;
7
3 7
2 3
A13
11;
3 1
1 2
5;
A23
3 1
11.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
2 5
1
2 5
17;
–22; A21
–9; A31
3 1
7
1 7
1
1 5
–11; A22
–8;
7
3 7
2 3
A13
11;
3 1
1 2
5;
A23
3 1
12.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
2
1
2 5
–22; A21
–9; A31
3
7
1 7
1
1 5
1
–11; A22
–8; A32
7
3 7
2
2 3
A13
11;
3 1
1 2
5;
A23
3 1
5
17;
1
5
9;
1
13.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
A11 A21 A31
1
.
X = A–1B, где A 2 3 1 , A 1
A
A
A
12
22
32
det A
3 1 7
A13 A23 A33
=11 ≠ 0,
3
A11
1
2
A12
3
2
1
2 5
–22; A21
–9; A31
3
7
1 7
1
1 5
1
–11; A22
–8; A32
7
3 7
2
2 3
A13
11;
3 1
1 2
5;
A23
3 1
5
17;
1
5
9;
1
1 2
A33
–7.
2 3
14.
x1 2 x2 5 x3 1,Пример 4. Решим матричным методом систему
2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
1 2 5
22 9 17
1
X = A–1B, где A 2 3 1 , A 1 11 8 9
11
11 5 7
3 1 7
=11 ≠ 0,
22 9 17 1
22 9 68
55
1
1
1
–1
11 8 36
X = A B=
11
8
9
1
33
11
11
11
4
11 5 28
22
11
5
7
5
3 .
2
Таким образом, x1 = 5; x2 = 3; x3 = –2.
Ответ. {5; 3; –2}.
15.
2. Метод Крамера.Определитель
a11 a12
a21 a22
... ...
an1 an 2
... a1n
... a2 n
,
... ...
... ann
составленный из коэффициентов при неизвестных в СЛАУ (3),
называется определителем системы (3).
Тh2 [Крамер, 1751]. Если определитель системы (3),
содержащей n уравнений с n неизвестными, отличен от 0: ≠ 0,
то система имеет единственное решение, которое может быть
найдено по формулам Крамера
1
2
n
x1 , x2 , ..., xn ,
где j (1 ≤ j ≤ n) – определитель, полученный из определителя
заменой j-го столбца на столбец свободных членов системы.
16.
17.
Доказательство. AX B X A 1B,x1
A11
x
A
1
2 12
...
x
n
A1n
A21
A22
...
A2 n
...
An1 b1
An 2
b
2 .
... ...
Ann bn
x1
A11b1 A21b2 ... An1bn
x
A b A b ... A b
1
22 2
n2 n
2 12 1
,
...
...
x
A
b
A
b
...
A
b
2n 2
nn n
n
1n 1
1
x j ( A1 jb1 A2 jb2 ... Anjbn ).
b1 a12
b2 a22
Например, A11b1 A21b2 ... An1bn
... ...
bn an 2
... a1n
... a2 n
1 и т. д.
... ...
... ann
1
2
n
x1 , x2
, ..., xn . ◄
18.
x1 2 x2 5 x3 1,2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
Пример 5. Решим методом Крамера систему
1 2 5
2 3 1 11 0.
3 1 7
1 2 5
1 3
1 1
3 1
1 1 3 1 1
5
2
4 1
4 7
1 7
4 1 7
1 ( 21 1) 2 ( 7 4) 5 ( 1 12) 22 22 55 55;
1 1 5
1 1
2 1
2 1
2 2 1 1 1
1
5
4 7
3 7
3 4
3 4 7
1 ( 7 4) 1 (14 3) 5 (8 3) 11 11 55 33;
1 2 1
3 1
2 1
2 3
3 2 3 1 1
2
1
1 4
3 4
3 1
3 1 4
1 ( 12 1) 2 (8 3) 1 (2 9) 11 22 11 22.
19.
x1 2 x2 5 x3 1,2 x1 3x2 x3 1,
3x x 7 x 4.
3
1 2
Пример 5. Решим методом Крамера систему
1 2 5
2 3 1 11 0.
3 1 7
1 55;
2 33;
3 22.
x1
1
, x2 2 , x3 3 ;
55
x1 1 5;
11
3 22
2 33
2.
x2
3; x3
11
11
Ответ. {(5; 3; –2)}.
Замечание. Методы обратной матрицы и Крамера применимы
для решения ТОЛЬКО тех систем, в которых количество
уравнений равно количеству неизвестных и, кроме того,
определитель матрицы системы отличен от 0: det A ≠ 0.
20.
Следствие. Если определитель системы равен нулю Δ=0, ахотя бы один из определителей Δ j≠0 то система не имеет
решения.
Следствие. Если определитель системы равен нулю Δ=0, и
все определители
Δ j =0, то система либо не имеет
решения либо имеет бесчисленное множество решений.
21.
Решение примеровПример. Найти неизвестную матрицу X из уравнения
1 2
2 -1
1 3 X 3 1
Решение. Исходное уравнение запишем в матричной форме
AX B
1 2 B= 2 1
A=
3 1
1 3
Матричное уравнение вида AX=B имеет решение, если матрицы
A и B– квадратные матрицы одинакового порядка и матрица A–
невырожденная.
В этом случае для матрицы A существует обратная матрица
AX=B
A-1 AX=A-1 B, где A-1 A=E
X=A-1 B
22.
Решение примеров-1
2
det A=
5 0
1 3
1 A11
A
A
det A 12
-1
A21
A22
1 2
A
1 3
A11= 3
AX=B
A-1 AX=A-1 B, где A-1 A=E
X=A-1 B
23.
Решение примеров-1
2
det A=
5 0
1 3
1 3
A
5 A12
-1
A11= 3
A12= -1
A21
A22
1 2
A
1 3
24.
Решение примеров-1
2
det A=
5 0
1 3
1 3 A21
A
5 1 A22
-1
A11= 3
A12= -1
A21= -1
1 2
A
1 3
25.
Решение примеров-1
2
det A=
5 0
1 3
1 3 1
A
5 1 A22
1 2
A
1 3
A11= 3
A22= -2
-1
A12= -1
A21= -1
26.
Решение примеров-1
2
det A=
5 0
1 3
1 3 2
A
5 1 1
-1
X=A-1 B
1 2
A
1 3
1 3 2 2 1
X -
5 1 1 3 1
1 3 2 ( 2) 3 3 ( 1) ( 2) 1
5
27.
Решение примеров-1
2
det A=
5 0
1 3
1 3 2
A
5 1 1
-1
X=A-1 B
1 2
A
1 3
1 3 2 2 1
X -
5 1 1 3 1
3 ( 1) ( 2) 1
1 3 2 ( 2) 3
5 ( 1) 2 ( 1) 3 ( 1) ( 1) ( 1) 1
28.
Решение примеров1 0 5 0
5 5 0
1
1
0
1 3 2 2 1
X -
5 1 1 3 1
3 ( 1) ( 2) 1
1 3 2 ( 2) 3
5 ( 1) 2 ( 1) 3 ( 1) ( 1) ( 1) 1
29.
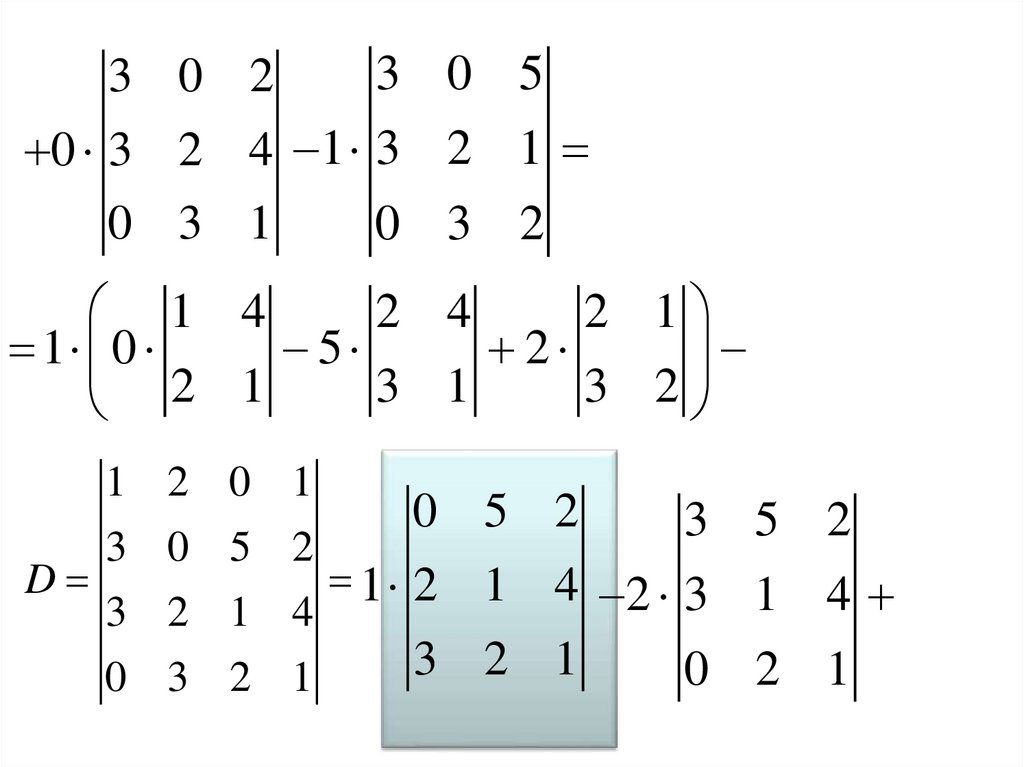
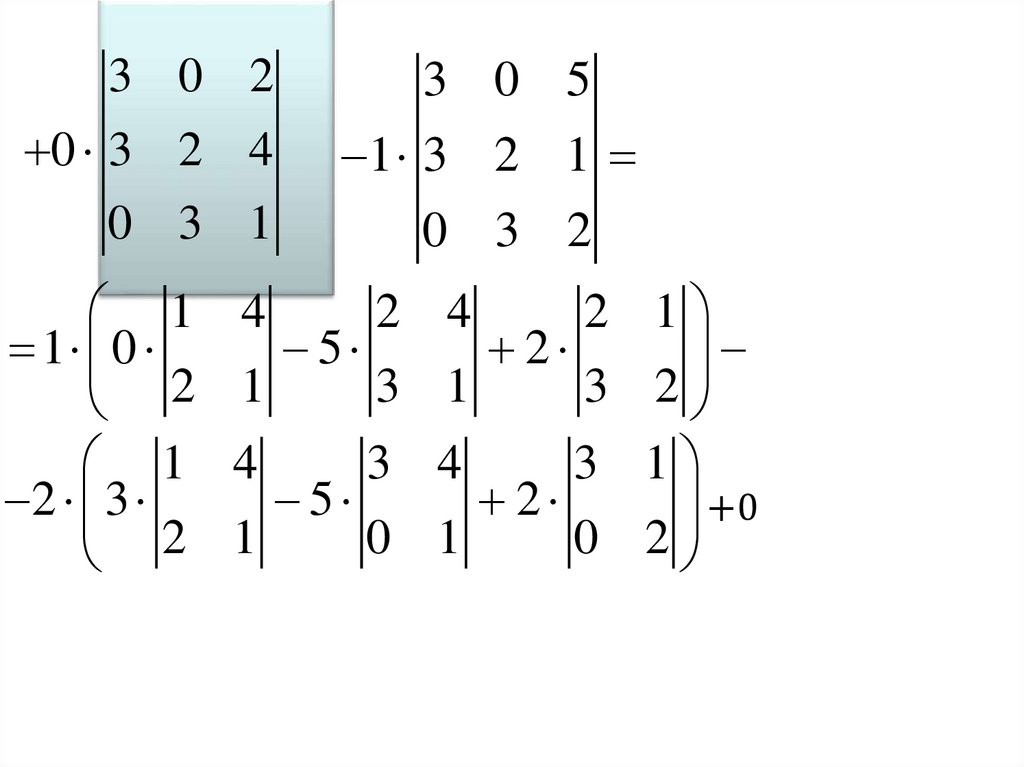
Пример. Вычислить определитель:Решение:
1 способ. Для вычисления
разложим
определитель
по
элементам первой строки:
1
3
D
3
0
2
0
2
3
0
5
1
2
1
0
2
1 2
4
3
1
1
3
3
0
2
0
2
3
0
5
1
2
1
2
4
1
3 5 2
5 2
1 4 2 3 1 4
0 2 1
2 1
30.
3 0 53 0 2
0 3 2 4 1 3 2 1
0 3 1
0 3 2
1
3
D
3
0
2
0
2
3
0
5
1
2
1
0
2
1 2
4
3
1
3 5 2
5 2
1 4 2 3 1 4
0 2 1
2 1
31.
3 0 53 0 2
0 3 2 4 1 3 2 1
0 3 1
0 3 2
1 4
2 4
2 1
1 0
5
2
3 1
3 2
2 1
1
3
D
3
0
2
0
2
3
0
5
1
2
1
0
2
1 2
4
3
1
5 2
3 5 2
1 4 2 3 1 4
2 1
0 2 1
32.
3 0 53 0 2
0 3 2 4 1 3 2 1
0 3 1
0 3 2
1 4
2 4
2 1
1 0
5
2
3 1
3 2
2 1
1 4
3 4
3 1
2 3
5
2
3
0 1
0 2
2 1
5 2
2 3 1 4
0 2 1
33.
3 0 20 3 2 4
0 3 1
1
1 0
2
1
2 3
2
3 0 5
1 3 2 1
0 3 2
4
2 4
2 1
5
2
1
3 1
3 2
4
3 4
3 1
5
2
+0
1
0 1
0 2
34.
3 0 20 3 2 4
0 3 1
1
1 0
2
1
2 3
2
3 0 5
1 3 2 1
0 3 2
4
2 4
2 1
5
2
1
3 1
3 2
4
3 4
3 1
5
2
+01
0 1
0 2
2 1
3 1
3 2
1 3
0
5
0 2
0 3
3 2
35.
1 5 10 2 1 2 3 7 5 3 2 61 3 1 5 9 52
1
1 0
2
1
2 3
2
4
2 4
2 1
5
2
1
3 1
3 2
4
3 4
3 1
5
2
+01
0 1
0 2
2 1
3 1
3 2
1 3
0
5
0 2
0 3
3 2
36.
1 5 10 2 1 2 3 7 5 3 2 61 3 1 5 9 52
2 способ : задача состоит в том, чтобы получить как можно
больше нулей в какой-нибудь из строк или столбцов, и, затем
разложить по этой строке (столбцу) определитель. Получим
нуль в первой строке в первом столбце. Для этого умножим
элементы четвертого столбца на (-1) и сложим с элементами
первого столбца, при этом определитель не изменится:
1
3
3
0
2
0
2
3
0
5
1
2
1
2
4
1
0
1
1
1
2
0
2
3
0
5
1
2
1
2
4
1
Умножим
четвертый
столбец на (-2) и
сложим со
вторым
столбцом
37.
0 01 4
1 6
1 1
0
5
1
2
1
2
4
1
1
3
3
0
1
2
4
1
0
1
1
1
2
0
2
3
0
5
1
2
Теперь разложим по
первой строке
полученный
определитель
2
0
2
3
0
5
1
2
1
2
4
1
Умножим
четвертый
столбец на (-2) и
сложим со
вторым
столбцом
38.
0 01 4
1 6
1 1
0
5
1
2
1
2
4
1
Теперь разложим по
первой строке
полученный
определитель
1 4 5
1 4 5
1 4
1 1 1 6 1 0 10 6
0 3 7
1 1 2
1 1 1
1 1
10 6
1 70 18 52
3 7






























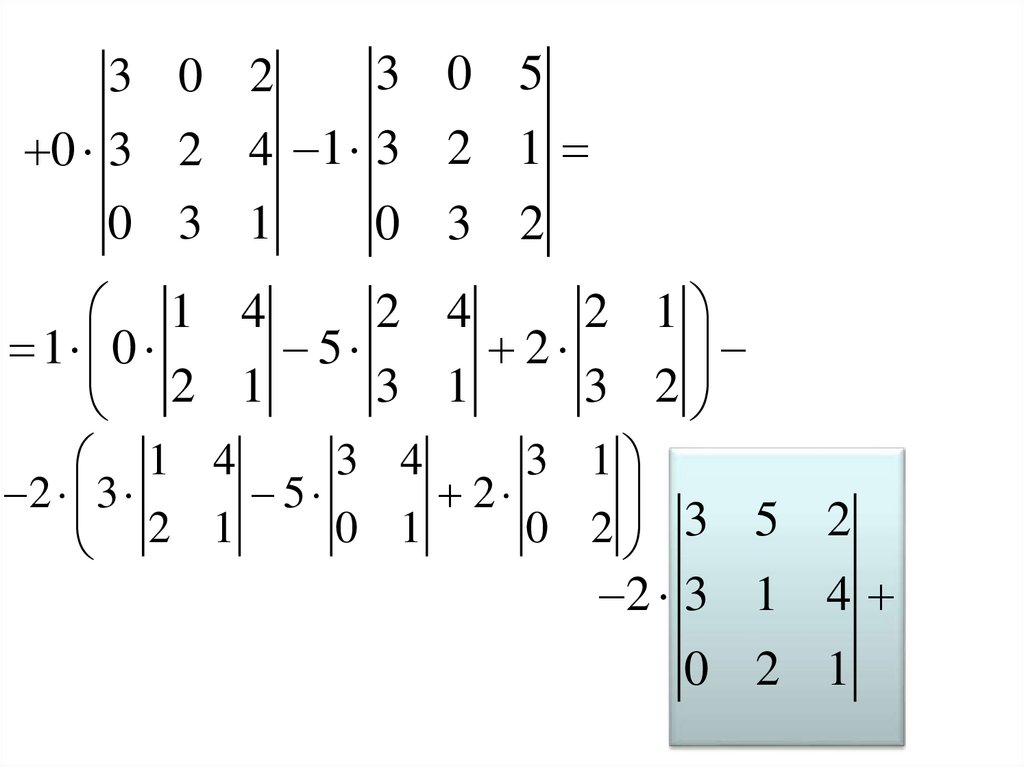
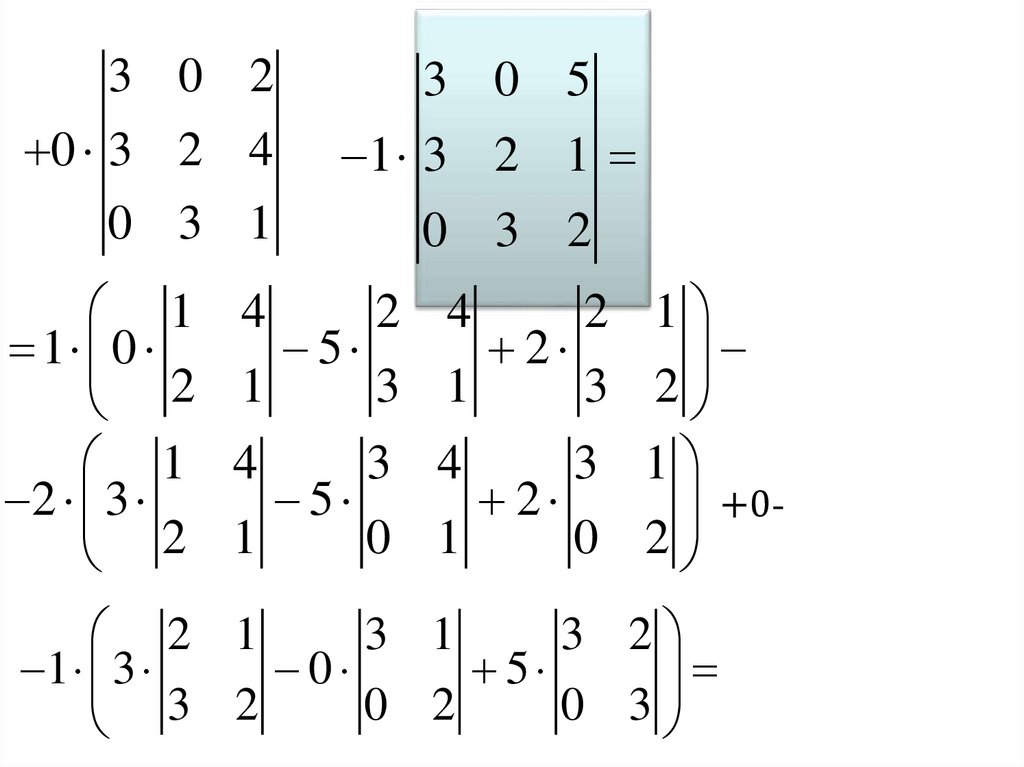
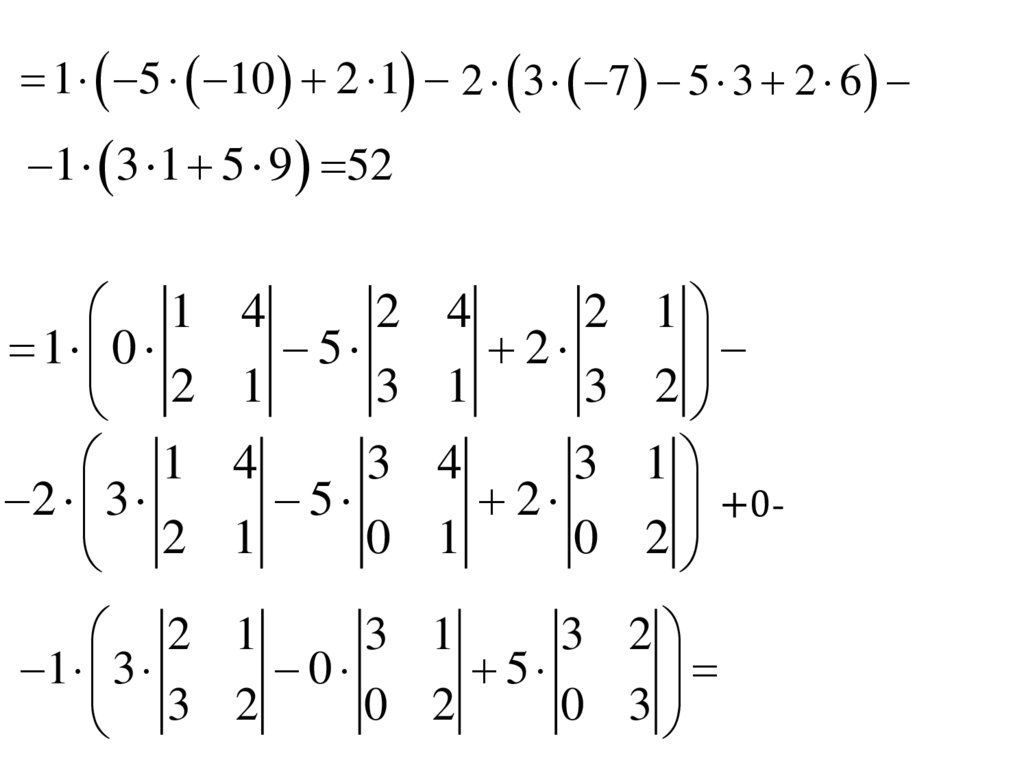



 Математика
Математика








