Похожие презентации:
1_4+3 Замечательные пределы 25
1.
Т8 (Лемма о сжатой переменной).WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWWWW
Ле́мма (греч. λημμα — предположение) — доказанное утверждение, полезное не само по
себе, а для доказательства других утверждений, «вспомогательная теорема».
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
Если в некоторой проколотой окрестности точки x0 выполняется неравенство
f (x) ≤ g(x) ≤ h(x) и существуют конечные пределы lim f ( x) lim h( x) A,
x x0
x x0
то существует
lim g ( x) A.
x x0
WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWWWW
Теорема о двух милиционерах — теорема в
математическом анализе о существовании предела у
функции, которая «зажата» между двумя другими
функциями, имеющими одинаковый предел.
Название теоремы происходит из того факта, что если два милиционера под руки ведут
задержанного в участок, то он вынужден идти вместе с ними.
В разных странах эта теорема называется по-разному: теорема сжатия, теорема о
промежуточной функции, теорема о двух карабинерах, теорема о сэндвиче (или правило
сэндвича), теорема о трёх струнах, теорема о двух жандармах, теорема о двух городовых и
пр.
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
2.
Т8 (Лемма о сжатой переменной).WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWWWW
Ле́мма (греч. λημμα — предположение) — доказанное утверждение, полезное не
само по себе, а для доказательства других утверждений, «вспомогательная
теорема».
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
Если в некоторой проколотой окрестности точки x0 выполняется
неравенство f (x) ≤ g(x) ≤ h(x) и существуют конечные пределы
lim f ( x) lim h( x) A,
g ( x) A.
то существует xlim
x x0
x x0
x
0
Доказательство. Зададим произвольное ε > 0.
Найдется проколотая δ-окрестность точки x0, в которой
|f (x) – A| < ε, |h(x) – A| < ε;
f (x) ≤ g(x) ≤ h(x)
f (x) – A ≤ g(x) – A ≤ h(x) – A.
|g(x) – A| < ε, 0 < |x – x0 | < δ
lim g ( x) A.
x x0
Доказано.
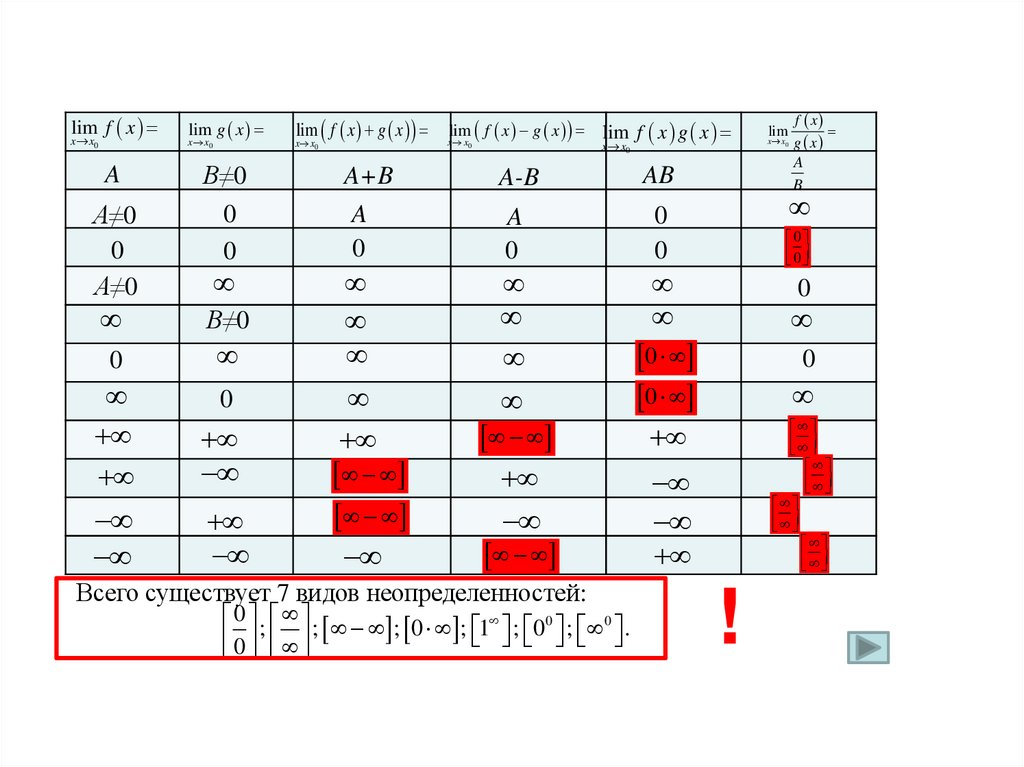
3.
lim f xx x0
A
A≠0
0
A≠0
lim g x
x x0
B≠0
0
0
B≠0
0
0
lim f x g x
x x0
lim f x g x
x x0
lim f x g x
x x0
A+B
A
0
A-B
AB
A
0
0
0
Всего существует 7 видов неопределенностей:
0
0
0
;
;
;
0
;
1
;
0
;
.
0
0
0
0
0
0
f x
g x
A
B
lim
x x0
0
!
4.
СИМВОЛИКА[0] – б.м.ф., [∞] – б.б.ф.;
0 0 0; 0 0 0; c 0 0;
1
1
;
0
0; ;
, a 1,
a
0, 0 a 1;
, a 1,
log a
, 0 a 1;
c ; ; c c 0 ;
, a 1,
log a 0
, 0 a 1;
Неопределенности
0
0
0
;
;
0
0
;
;
;
1
;
.
0
5.
§ 7. Замечательные пределыTh. 1. Первый замечательный предел
sin x
lim
1.
x 0 x
(Этот предел является неопределенностью типа 0 .)
0
sin x
Доказательство.
– четная функция, x → 0.
x
π
Пусть 0 x , x – радианная мера угла AOB в единичном круге.
2
2
1
1
π
1
S AOB SсекAOB S CAO , 1 1 sin x
x 1 (1 tg x),
2
2
2π
sin x
x
tg x
x
1
, 1
sin x x tg x,
,
sin x sin x sin x
sin x cos x
1
x→0
sin x
sin x
lim
1. ◄
cos x
1.
x 0 x
x
Замечание. Первый замечательный предел используется при раскрытии
0
неопределенности
вида
при
вычислении
пределов
с
0
тригонометрическими выражениями.
6.
Следствия:sin α x
1; ► α x t , t 0 lim sin t 1. ◄
α x 0 α x
t 0
t
1. lim
2. α(lim
x ) 0
tg α( x)
1;
α( x)
tg α( x)
sin α( x)
1
lim
lim
1.
α( x ) 0 α( x)
α( x ) 0
α( x) cosα( x)
◄
замена
arcsin α( x)
arcsin α( x) arcsin α( x) y
y
lim
1.
3.
► lim
lim
1. ◄
α( x ) 0
α( x ) 0
α( x)
α( x)
y
0
α( x) sin y
sin y
y 0
arc tgα( x)
1.
4. α(lim
x ) 0
α( x)
Упр. 1. Доказать следствие 4.
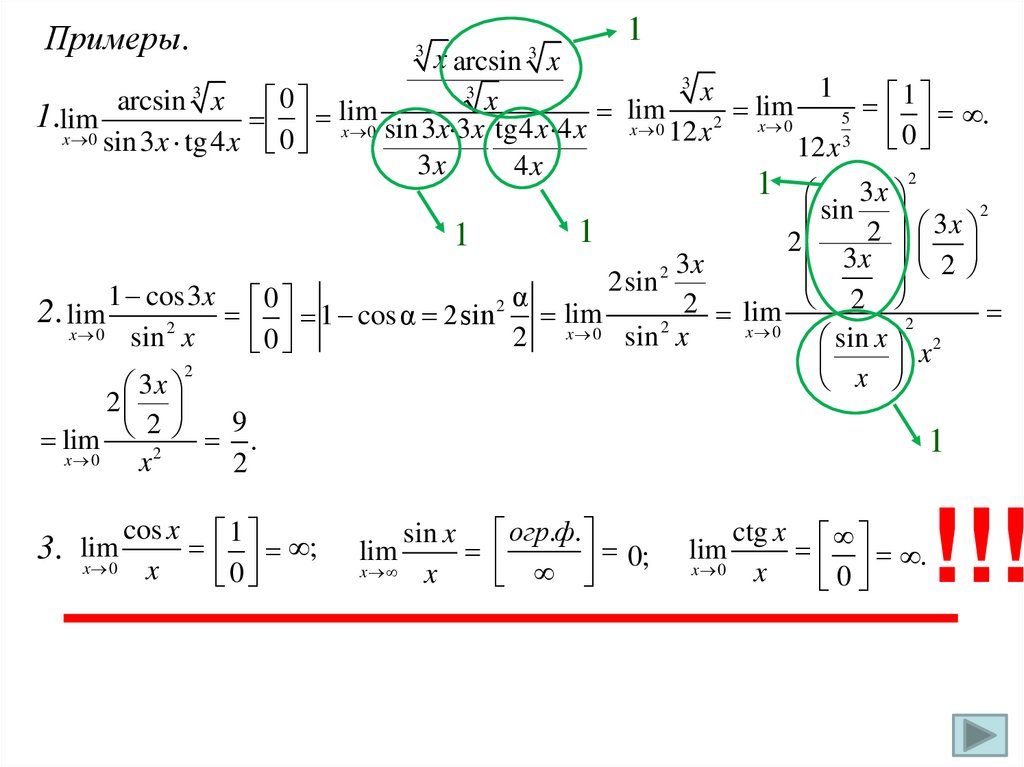
7.
Примеры.3
3
1
x arcsin x
3
1
3
3
x
1
x
arcsin x 0 lim
lim
lim
.
5
1.lim
x 0 sin 3x 3x tg4 x 4x x 0 12 x 2 x 0
x 0 sin3 x tg 4 x 0
12 x 3 0
3x
4x
1 3x 2
2
sin
3
x
2
1
1
2
3x 2
2 3x
2sin
1 cos3x 0
α
2
2 lim 2
2. lim
lim
1
cosα
2sin
2
2
2
x
0
x
0
x 0
sin x
sin x
2
sin x x 2
0
2
x
3x
2
9
2
lim 2 .
1
x 0
x
2
cos x 1
;
x 0
x
0
3. lim
sin x огр.ф.
0;
lim
x
x
ctg x
lim
.
x 0
x
0
!!!
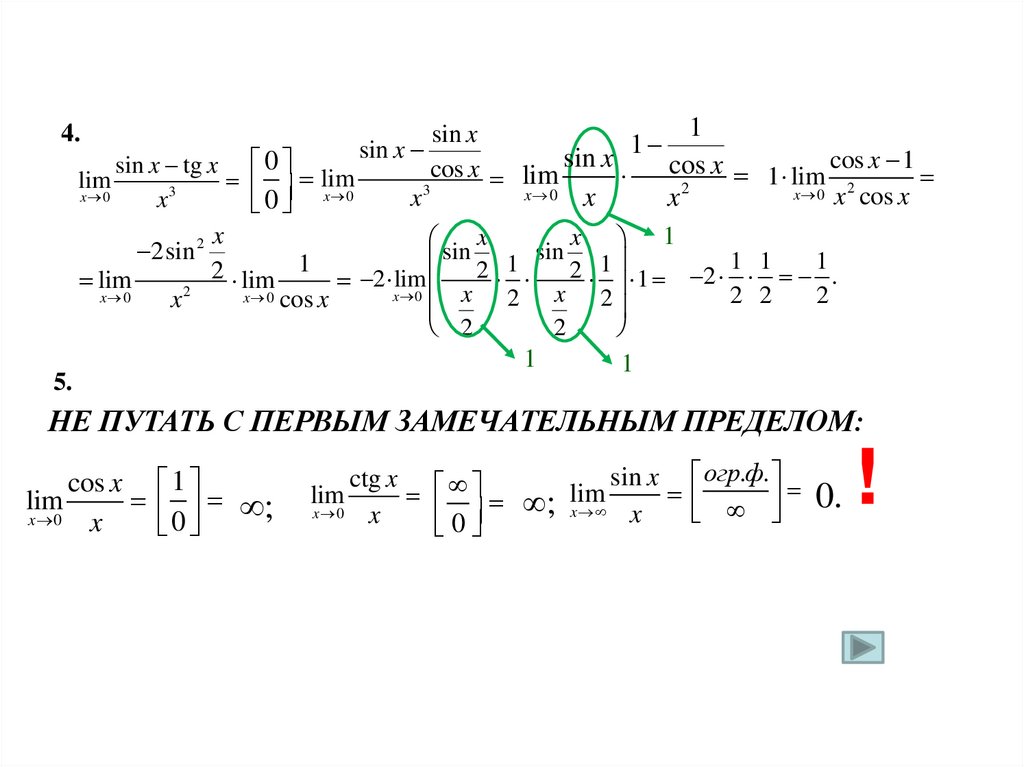
8.
4.sin x tg x 0
lim
3
x 0
x
0 x 0
lim
lim
x 0
5.
2sin 2
x2
1
sin x
1
cos x 1 lim cos x 1
cos x lim sin x
x 0 x 2 cos x
x 0
x
x2
x3
sin x
x
x
x 1
sin
sin
2 1
2 1 1 2 1 1 1 .
2 lim 1 2 lim
x
x 0
x 2
x 0 cos x
2 2
2
2
2
2
1
1
НЕ ПУТАТЬ С ПЕРВЫМ ЗАМЕЧАТЕЛЬНЫМ ПРЕДЕЛОМ:
cos x 1
lim
;
x 0
x
0
sin x огр.ф.
ctg x
lim
lim
0.
x 0
0 ; x x
x
!
9.
Второй замечательный пределЗадача, приводящая ко второму замечательному пределу,
рассмотрена швейцарским математиком Я. Бернулли в 1690 г.
была
WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWW
Я́коб Берну́лли
(нем. Jakob Bernoulli)
(1654–1705)
швейцарский математик. Один из основателей теории вероятностей
и математического анализа, внес огромный вклад в развитие
аналитической геометрии и зарождение вариационного исчисления.
Ввел значительную часть современных понятий теории
вероятностей, в 1713 г. посмертно был издан его трактат
«Искусство предположений» (Ars conjectandi) – монография по
теории вероятностей, статистике и их практическому применению, итог комбинаторики и
теории вероятностей XVII в.
Якоб Бернулли является родоначальником известной научной династии, многие члены
которой в XVII-XVIII вв. внесли существенный вклад в науку. В частности, к этой
династии принадлежат 9 крупных математиков и физиков (из них 3 великих), а также
известные историки, искусствоведы, архитекторы, юристы и др. Историки насчитали в
науке и культуре не менее 30 знаменитых представителей семьи Бернулли.
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
10.
Второй замечательный пределЗадача, приводящая ко второму замечательному пределу, была рассмотрена
швейцарским математиком Я. Бернулли в 1690 г.
Задача о непрерывном начислении процентов
Пусть Q0 – первоначальный вклад в банк.
Если банк выплачивает ежегодно p% годовых, то вклад в конце года
составит Q Q 1 p
0
100
p
Q Q0 1
100n
n
1
q
Для простоты рассмотрим Q0 = 1, p = 100%, т.е. n 1
n
q1 2; q2 (1,5)2 2, 25;
q4 2, 44;
q12 2,61;
n
q365 2,715;...
11.
Второй замечательный предел1
Я. Бернулли показал, что существует предел lim 1
n
n
и его значение заключено между 2 и 3.
n
n
1
lim
Обозначение n 1 e ввел Л. Эйлер в 1731 г.
n
n
1
qn 1
n
2
q1 2; q2 (1,5) 2, 25;
q4 2, 44;
q12 2,61;
q365 2,715;...
12.
WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWWЛеона́рд Э́йлер
(нем. Leonhard Euler)
(1707–1783)
швейцарский, немецкий и российский математик и механик.
Впервые увязал математический анализ, алгебру, геометрию,
тригонометрию, теорию чисел и другие дисциплины в
единую систему, добавив при этом немало собственных
открытий. Был виртуозным алгоритмистом и всегда старался
довести
свои
открытия
до
уровня
конкретных
вычислительных методов.
Автор более чем 850 работ. В его работах использовались
продуманная терминология и математическая символика, в
Большой мере сохранившиеся до наших дней. Значительная часть математики
преподается с тех пор «по Эйлеру» почти без изменений.
Почти полжизни провел в России, куда приехал в возрасте 20 лет по приглашению
Петра I в период организации Российской академии наук. Уже через год пребывания в
России он хорошо знал русский язык и часть своих сочинений (особенно учебники)
публиковал на русском.
По отзывам современников, Эйлер был жизнерадостен, общителен, практически ни с
кем не ссорился, охотно помогал коллегам и молодежи.
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
13.
Th.2. Bторой замечательный пределx
1
1
1 z z e,
lim 1 lim
x
x z 0
где е = 2,718281828459045… .
(Используется при раскрытии неопределенности вида [1∞].)
Следствия:
1. lim 1 α(x)
1
α(x )
α(x ) 0
e, где (x) → 0, при x → a.
ln(1 x)
1.
x 0
x
2. lim
1
1
ln(1 x) 0
lim ln(1 x) limln(1 x) x
► lim
x 0
0 x 0 x
x 0
x
1
x
ln lim(1 x) ln e 1. ◄
x 0
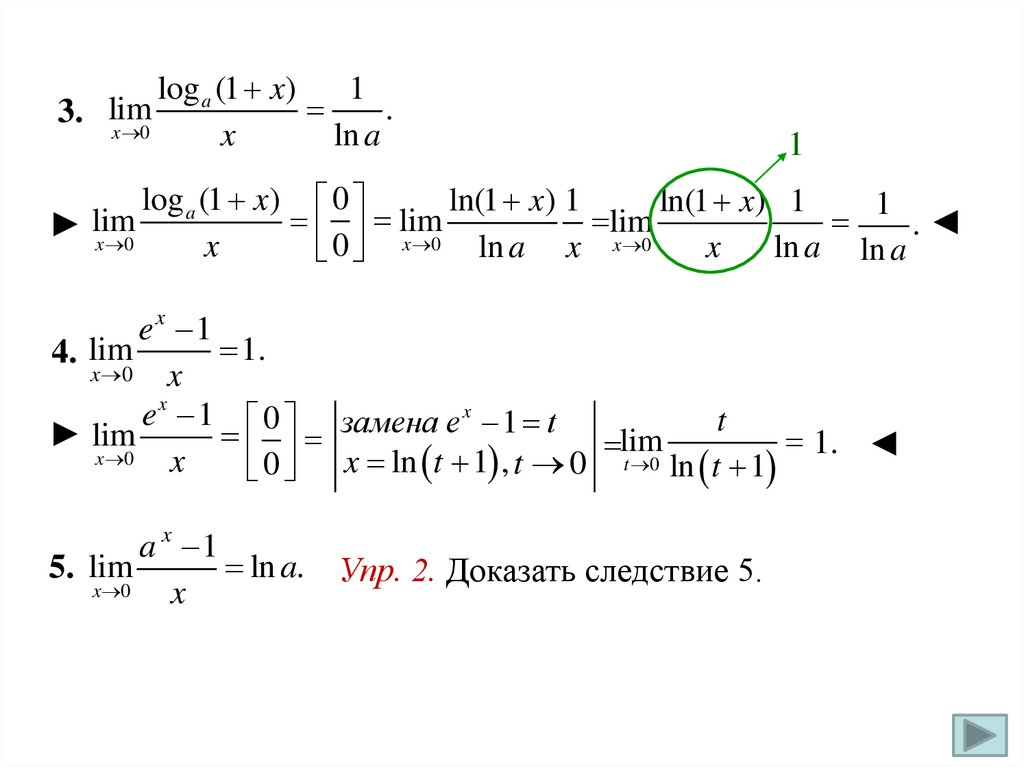
14.
log a (1 x)1
.
3. lim
x 0
x
ln a
1
log a (1 x) 0
ln(1 x) 1
ln(1 x) 1
1
lim
lim
lim
.◄
► x 0
x
0
x
0
x
ln a x
x
ln a ln a
0
ex 1
1.
4. lim
x 0
x
e x 1 0 замена e x 1 t
t
► lim
1. ◄
0 x ln t 1 , t 0 lim
x 0
t 0 ln t 1
x
a x 1
ln a. Упр. 2. Доказать следствие 5.
5. lim
x 0
x
15.
Для раскрытия неопределенности вида 1 часто используется второй замечательный предел и следствия из негоВыполняются следующие тождественные преобразования
Сначала в основании степени нужно выделить ту бесконечно
малую, которая прибавляется к единице и в показателе степени
записать в точности обратную ей величину (если в основании
имеется разность, то знак минус относится к бесконечно малой).
Сконструированная таким образом величина будет иметь своим
пределом число е, это выражение целесообразно заключить в
скобки.
Затем в показателе степени, основанием которой является
выражение в скобках, записать исходный показатель степени с
поправочным множителем, который подбирается так, чтобы при
возведении степени в степень (т.е. при перемножении всех
показателей) получить исходное выражение.
Наконец, находится предел показателя степени, основанием
которой является выражение в скобках, и записывается ответ.
16.
Примеры.(1 2 x )
(1 2 x ) 1 lim
1. lim
x
0
x 0
1
2 2 x2
4
2 x2
8
e8 .
(cos 2 x)ctg x [1 ] lim (1 (cos 2 x 1))ctg x lim
(1 2sin x)
2. lim
x 0
x 0
x 0
2
ctg x
1
cos x
2
( 2sin x) ctg x
lim 2sin 2 x
lim 2sin x cos x
2
x 0
sin x
( 2sin x)
x 0
lim (1 ( 2sin x))
e
e
x 0
e 0 1.
2
x 1
x 1
x 1
3. lim
x
2
lim 1
x
x 1
x 1
[1 ] lim 1
1
x
x 1
x 1
2
2
e
lim 2
x
x 1
x 1 x 1
lim
1
x
x 1
e 2.
x 1 x 1 2
2
1
x 1
x 1
x 1
x 1
17.
1x 1
1
x 1
x
4. xlim
xlim
2 x 1
1
2
x
x 1
1
0.
2
1
x
x
ln(1 )
ln(1
)
ln( x 2) ln 2 0
1 1
2
2
lim
.
lim
5. lim
x
0
x 0
x
0
x
x
x
2 2
0
2
x
2
1
2
2 x 3x 0
2
x 3
x
lim3
lim3
ln
lim
ln
.
6. x 0
x
0
x
0
x
3
x
3
0
ln
2
3
18.
Некоторые другие замечательные пределы.tg x
lim
1
x 0 x
arcsin x
1
x 0
x
lim
lim
x 0
arctg x
x
1
log a (1 x)
ln( 1 x )
lim
log a e,0 a 1
lim
1 x 0
x
x 0
x
a x 1
e x 1
lim
ln a, a 0
lim
1
x
0
x 0
x
x
(1 x)a 1
lim
a, a
x 0
x
Замечательные пределы - термин, использующийся в советских и российских
учебниках по математическому анализу для обозначения некоторых широко
известных математических тождеств со взятием предела. Замечательны они
потому, что они уже доказаны великими математиками и нам остается лишь
пользоваться ими для удобства нахождения пределов.
Замечательных пределов существует несколько, но самыми известными
являются первый и второй замечательные пределы. Их замечательность
состоит в том, что они имеют широкое применение и с их помощью можно
найти и другие пределы, встречающиеся в многочисленных задачах.
19.
§ 8. Сравнение б.м.ф.Эквивалентные б.м.ф.
Пусть (x) и β(x) – б. м. ф. при x → a, причем
β x
lim
A.
x a x
Тогда
1) если А=1, то (x) и β(x) называются эквивалентными
б. м. ф. при x → a, что записывается в виде (x) ~ β(x);
2) A ≠ 0 и A ≠ ∞, то (x) и β(x) – б. м. ф. одного порядка
малости при x → a;
3) А = 0, то β(x) есть б. м. ф. более высокого порядка малости,
чем (x) при x → a, что записывается в виде β(x) = o( (x));
4) А = ∞, то (x) есть б. м. ф. более высокого порядка
малости, чем β(x) при x → a, что записывается в виде
(x) = o(β(x)).
20.
5) если предел А не существует, то говорят, что б.м.ф. (x) иβ(x) при x → x0 несравнимы.
21.
Пример.α x x 1, β( x) 3x 2 x 2 , γ( x) x 2 1, μ( x) x 2 x 1
2
б.м.ф. при x → 1.
3x 2 x 2
β( x)
( x 1)(2 x)
lim
lim
lim
lim(2 x) 1,
x 1
x 1 α( x)
x 1
x
1
x 1
x 1
(x) ~ β(x);
2
( x 1)( x 1)
x
1
γ( x)
lim( x 1) 2,
lim
lim
lim
x 1
x 1
x 1 x 1
x 1 α( x)
x 1
(x) и γ(x) одного порядка малости;
( x 1)( x 1)
x2 2 x 1
μ( x)
lim( x 1) 0,
lim
lim
lim
x 1
x 1
x 1
x 1 α( x)
x 1
x 1
μ(x) = o( (x)).
22.
Свойства эквивалентных бесконечно малых функций:1. Если (x) ~ β(x), то β(x) ~ (x).
2. Если (x) ~ β(x) и β(x) ~ γ(x), то (x) ~ γ(x).
3. Если (x) и β(x) – эквивалентные б.м.ф. при x → a, то их
разность есть б.м.ф. более высокого порядка, чем каждая из
них.
Если (x) ~ β(x), то (x) – β(x) = o( (x)), (x) – β(x) = o(β(x)).
Доказательство. Пусть (x) ~ β(x) при x → a
β x
α x β x
lim
lim 1
1 1 0 α x β x o α x
x a
x a
α x
α x
Аналогично для β(x). ◄
4. Предел отношения двух б.м.ф. не изменится, если каждую из
них или одну из них заменить эквивалентной ей б.м.ф.
Если (x) ~ ′(x) и β(x) ~ β′(x), то
β x
β x
β x
β x
lim
lim
lim
lim
.
x a x
x a x
x a x
x a x
23.
Таблица эквивалентных бесконечно малых функцийПусть (x) → 0, при x → а.
Тогда
1. sin α(x) ~ α(x)
2. tgα(x) ~ α(x)
3. arcsin α(x) ~ α(x)
4. arctgα(x) ~ α(x)
α 2 (x)
5. 1 cosα(x) ~
2
eα(x ) 1 ~ α(x)
7. ln(1 α(x)) ~ α(x)
α(x )
1 ~ α(x)lna
8. a
α(x)
9. log a (1 α(x)) ~
ln a
α(x)
n
10. 1 α(x) 1 ~
n
6.
24.
Примеры.arctg(2x) 2x
sin(5 x) 5x,
2
sin(5 x) arctg(2x) 1 x 1
x
2
5 x 2
2
0
, e
1 5x
1. lim
1 x 1
3
2
5 x 2
2
x 0
ln(1 x x ) e
1
0 ln(1 x3 x 2 ) ( x3 x 2 )
2
x
5 x 2x
2
1
lim 3
lim
1.
x 0 ( x x 2 ) 5 x 2
x
0
( x 1)
2
sin x 0
0.
x π
π
x
2. lim
arctg(k sin x) k sin x
k sin x 1
cos(sin
x
)
lim
2k.
1
x π 1
arctg(k sin x) cos(sin x) 0
sin x
3. lim
1 sin x 1 1 sin x
x π
2
1 sin x 1
0
2
x2
1
cos x 1 cos x 1
2
sin x
sin x 1
sin x x
sin x tgx 0
cos
x
cos
x
lim
lim
4. lim
sin x3
sin x3
sin x3
x 0
x
0
x
0
cos
x
1
2
1
2
1
2
1
0
3
x
1
.
lim 3 2
x 0 x ln 2
2ln 2
2
sin x3
1 x3 ln 2
25.
Замечание. При вычислении пределов заменять б.м.ф. наэквивалентные б.м.ф. можно только в частном и
произведении, а в сумме или разности – нельзя.
Т.Сумма двух б.м.ф. разных порядков эквивалентна б.м.ф. низшего порядка
малости, т.е. если (x) и β(x) - б.м.ф. при x → x0, (x) = o(β(x)) при x → x0,
то (x) + β(x) ~ β(x).
Доказательство.
x
x +β x
1 0 1 1, т.е. (x) + β(x) ~ β(x) при x → x0.
lim
xlim
x
0
x x0
β x
β x
Доказано.
Слагаемое, эквивалентное сумме б.м.ф. называется главной частью этой
суммы.
2 x 3x 2 4 x3 0 2 x 3 x 2 4 x 3 2 x
Пример. lim
0 при x 0
x 0
sin 5 x
2x 2
2x
sin 5 x 5 x
lim
.
lim
x 0 5 x
x 0 sin 5 x
5
при x 0
26.
§ 9. Вычисление пределов.Раскрытие неопределенностей
Вычисление пределов начинается с подстановки вместо х предельного
При нахождении предела отношения
значения!
1. Неопределенность вида двух многочленов P(x) и Q(x) при x → ∞
числитель
и
знаменатель
дроби
целесообразно разделить на xn, где n –
Примеры:
высшая степень этих многочленов.
0
7
3
2
2
3
2 x3 7 x 3
2
x
x
;
lim
1. lim 2
x 3 x 3 x 4
x 3 3 4 0
x x 2 x3
0
2 7
3
2x 7x 3
2
3
0
x
x
x
lim
2.
lim
0;
3
2
x 3 x 3 x 4
3
4
3
x 3
x x3
2
27.
§ 9. Вычисление пределов.Раскрытие неопределенностей
Вычисление пределов начинается с подстановки вместо х предельного
При нахождении предела отношения
значения!
1. Неопределенность вида двух многочленов P(x) и Q(x) при x → ∞
Примеры:
числитель
и
знаменатель
дроби
целесообразно разделить на xn, где n –
высшая степень этих многочленов.
0
7
3
2
3
2 x3 7 x 3
2
x
x
3. lim 3
lim
;
2
x
3 4
x 3 x 3 x 4
3 3 3
x x
2
0
2 7
3
2x 7x 3
2
3
0
x
x
x
lim
2.
lim
0;
3
2
x 3 x 3 x 4
3
4
3
x 3
x x3
2
28.
§ 9. Вычисление пределов.Раскрытие неопределенностей
Вычисление пределов начинается с подстановки вместо х предельного
При нахождении предела отношения
значения!
1. Неопределенность вида двух многочленов P(x) и Q(x) при x → ∞
Примеры:
числитель
и
знаменатель
дроби
целесообразно разделить на xn, где n –
высшая степень этих многочленов.
7
3
2
3
2 x3 7 x 3
2
x
x
lim
3. lim 3
;
2
x
3 4
x 3 x 3 x 4
3 3 3
x x
2
Итого:
a0
b , если m n,
m
m 1
Pm ( x)
a0 x a1x ... am 0
lim
lim
0 , если m n,
x Q ( x )
x b x n b x n 1 ... a
n
0
1
n
, если m n.
29.
2. Неопределенность вида0
0
Cократить дробь на (x – a)
P x 0
x a Q x
0
2.1 lim
При раскрытии неопределённости
в случае отношения
многочленов нужно в числителе и знаменателе выделить
множитель вида «переменная минус её предельное значение» и
сократить дробь. После этого неопределённость может
исчезнуть и уже можно пользоваться арифметическими
свойствами или особыми случаями, или же нужно снова
применить описанный приём.
При этом нужно очень чётко представлять себе, что согласно
определению предела функции в точке деления на ноль не
происходит («На 0 делить нельзя!»), выделенный множитель
есть величина бесконечно малая и отличная от нуля.
Для выделения множителя (х - а) можно использовать деление
многочлена на многочлен «уголком», формулы сокращённого
умножения или удачную группировку.
30.
2. Неопределенность вида0
0
Cократить дробь на (x – a)
P x 0
x a Q x
0
2.1 lim
Примеры:
3
2
x
1
x
2x 3 2 3 1
2
2 x2 5x 3 0
lim
lim
1. lim 2
.
x 1 x 1 x 5
x
1
x 1 x 6 x 5
x 5 1 5 4
0
ax 2 bx c a( x x1 )( x x2 )
x 1 x 2 x 2
x x 2 0
2. lim
0 lim
x 1 4 x 2 5 x 1
x 1
4 x 1 x 1
3
2
x2 2 x 2 1 2 2 5
lim
.
x 1
4x 1
3
4 1
2
_ x3 x 2 2 x 1
x3 x 2
2
x
2x 2
2
_ 2x 2
2 x2 2 x
_ 2x 2
2x 2
0
31.
2. Неопределенность вида0
0
Cократить дробь на (x – a)
2.2 в случае иррациональных выражений
следует домножить на сопряженное выражение
При этом
сумму (разность) квадратных корней умножаем на их разность (сумму);
сумма (разность) кубических корней умножается на неполный квадрат их
разности (суммы) и т. д.
Примеры:
2x 1 9
2 x 1 3 0 lim 2 x 1 3 2 x 1 3 lim
x 4
1. lim
x 4
x 4
x 4 2x 1 3
x 4
x 4 2x 1 3
0
2 x 4
2 x 8
2
2
1
.
lim
lim
lim
x 4
x 4 2 x 1 3 x 4 x 4 2 x 1 3 x 4 2 x 1 3 3 3 3
2
3
3
x 1 x 1 x x 1
x 1 0
2. lim 3
lim 3
2
x 1
x 1 0 x 1 x 1 3 x 3 x 1 x 1
2
2
3
3
3
3
x 1 x x 1
x
x 1 3
lim
lim
.
x 1
x
1
x 1
2
x 1 x 1
32.
2. Неопределенность вида0
0
Cократить дробь на (x – a)
2.3 В случае тригонометрических выражений
Применяем первый замечательный предел (его следствия) или
эквивалентные б.м.ф.
3. Неопределенность вида 1
Применяем второй замечательный предел
4. Неопределенности вида , 0
0
При помощи преобразований сводим к неопределенностям вида
0
или .
33.
Методы раскрытия неопределенностейВсего существует 7 видов неопределенностей:
0
0
0
0
0
;
;
;
0
;
1
;
0
;
.
0
!
• разделить числитель и знаменатель на х в наивысшей степени
• сократить на множитель (x - x0)
• в случае иррациональных выражений избавиться от иррациональности
домножив и разделив на сопряженное выражение
• в случае тригонометрических выражений использовать первый
замечательный предел
• использовать эквивалентные б.м.ф.
, 0
0
или
• преобразовать к неопределенности вида
0
1 • использовать второй замечательный предел
1 , 00 , 0 • преобразовать путем логарифмирования
34.
Примеры:x x 1 x x x 1 x
1. lim x x 1 x [ ] lim
2
2
2
x
lim
x
x2 x 1 x
1
1
x 1
x
lim
2
x
1 1
x x 1 x
1 2 1
x x
x
x2 x 1 x2
x x 1 x
2
1 0
1;
1 0 0 1 2
lim
x
1
1
x2 2 x
1 1
x2 2 x
3
2. lim
[ ] lim
2
x 1 x 1
x
1
x 1 x 1 x x 1
x 1
0 0
0
x2 x 1 x2 2 x
x 1
lim
lim
2
2
x 1 x 1 x x 1
x 1 x 1 x x 1 0
x 1
1
1
lim
lim
;
x 1 x 2 x 1
x 1 x 1 x 2 x 1
3
35.
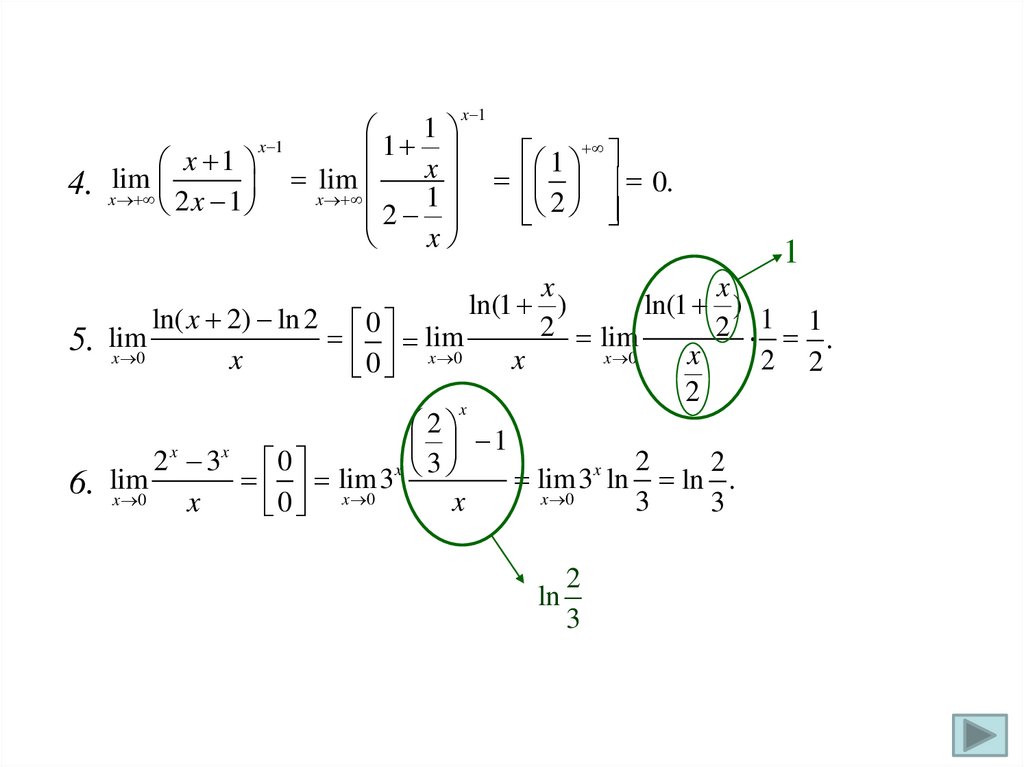
tg x 2 x 21
tg x 2 x 2 0
2
2
tg x 2 x [ 0] lim
lim
3. lim
2
2
2
x
0
x 0 x
x 0
x
x
x
0
1
tg x
x
lim 2 2 tg x x lim 2 2 lim 2 [ 2] .
x 0
x 0 x
x 0 x
x
π
x
4
π
π
4. limπ tg2 x tg x [ 0] y 0 lim tg2 y tg y
y 0
4
x
4
4
π
x y
4
cos 2 y sin y 0
π
lim
lim tg 2 y tg y limctg 2 y tg y
y
0
y 0
y
0
sin
2
y
cos
y
2
0
y
sin y y
sin 2 y 2y
y 1
.
cos y 1 lim
y 0 2 y
2
cos 2 y 1
y 0
36.
ВидыМетоды нахождения
неопределённостей
необходимо разделить числитель и знаменатель на
х в наивысшей степени.
упростить выражение функции для этого либо
раскладывают
на
множители,
либо
преобразовывают функцию с помощью формул
сокращенного умножения, тригонометрических
формул, либо домножают на сопряженное, что
позволяет в дальнейшем сократить члены,
стремящиеся к нулю.
применить второй замечательный предел
преобразовать неопределенность к виду
или





























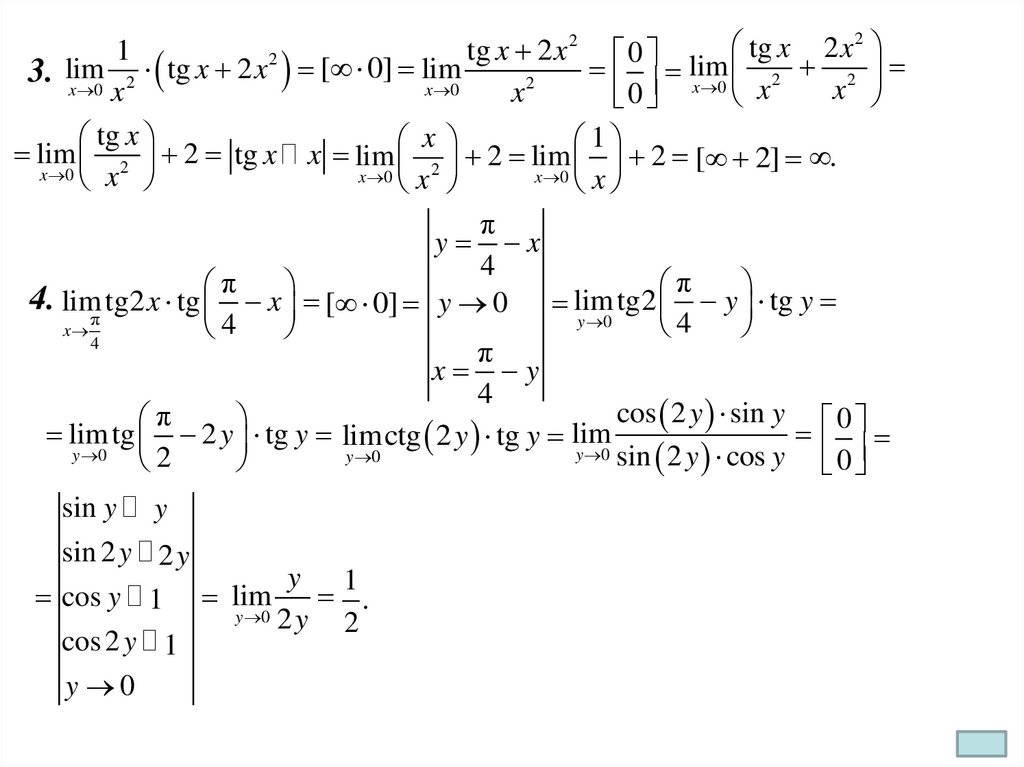

 Математика
Математика








