Лекция_2_формулы_20.09.2023

1. Лекция №2 Вычислительная математика

Санкт-Петербургский политехнический университет Петра Великого
Лекция №2
Вычислительная математика
Воскобойников С.П.
Доцент ВШ ПИ ИКНТ, к.ф.-м.н.
voskob_sp@spbstu.ru
20.09.2023

2. Содержание

• Элементарные матрицы.
• Обратная матрица к элементарной.
• Матрицы перестановки, исключения,
Хаусхолдера и их свойства
• Матрицы Гивенса (вращения) и их свойства
• Цепочки вращений.

3. Элементарные матрицы

Э E u vT
E единичная матрица,
вещественные векторы размерности n
Э E uvT
u1
u
u1v1 u1v2 ... u1v j ... u1vn
2
u
v
u
v
...
u
v
...
u
v
2 1
2 2
2 j
2 n
uvT v1 v2 ... vn
...
un v1 un v2 ... un v j ... un vn
un
u1
u
2
u
un
i, j ый элемент матрицыuvT uvT ij ui v j
число
v1
v
2
v
vn

4. Обратная матрица к элементарной

1 u T v
Э 1 E u vT
u T v 1
u1
u
2
. n
T
v u v1 v2 ... vn vi ui v, u
. i 1
.
un
vT u u T v
v, u u, v
ЭЭ 1 E u vT E u vT E u vT u vT u vT u vT
E u vT u vT u vT u vT E u vT u vT
T
T
v u 0
v
u 1
T
1 v u

5. Пример элементарной матрицы

2
u 3
4
1 vT u
5
v 6
7
vT u 5
2
T
1 v u
2
2
6 7 3 5 2 6 3 7 4 0
vT u 1
4
2
10 12 14
uvT 3 5 6 7 15 18 21
4
20 24 28
1 0 0
10 12 14 21 24 28
Э 0 1 0 2 15 18 21 30 37 42
0 0 1
20 24 28 40 48 55
1 0 0
10 12 14 19 24 28
Э 1 0 1 0 2 15 18 21 30 35 42
0 0 1
20 24 28 40 48 57

6. Собственные числа и собственные векторы элементарных матриц

Эx x
x1 u
vT xi 0, i 2,3,..., n
1 1 vT u
i 1,
i 2,3,..., n
1 1 vT u
Эu E uvT u u uvT u 1 vT u u
Эxi E uvT xi xi uvT xi
vT xi 0, i 2,3,..., n
i 1,
i 2,3,..., n

7. Выполнение операции умножения на элементарную матрицу

z Эy
,
Эy E uvT y y uvT y y vT y u
~ n операций вместо n2
2n ячеек памяти для u, v вместо n2

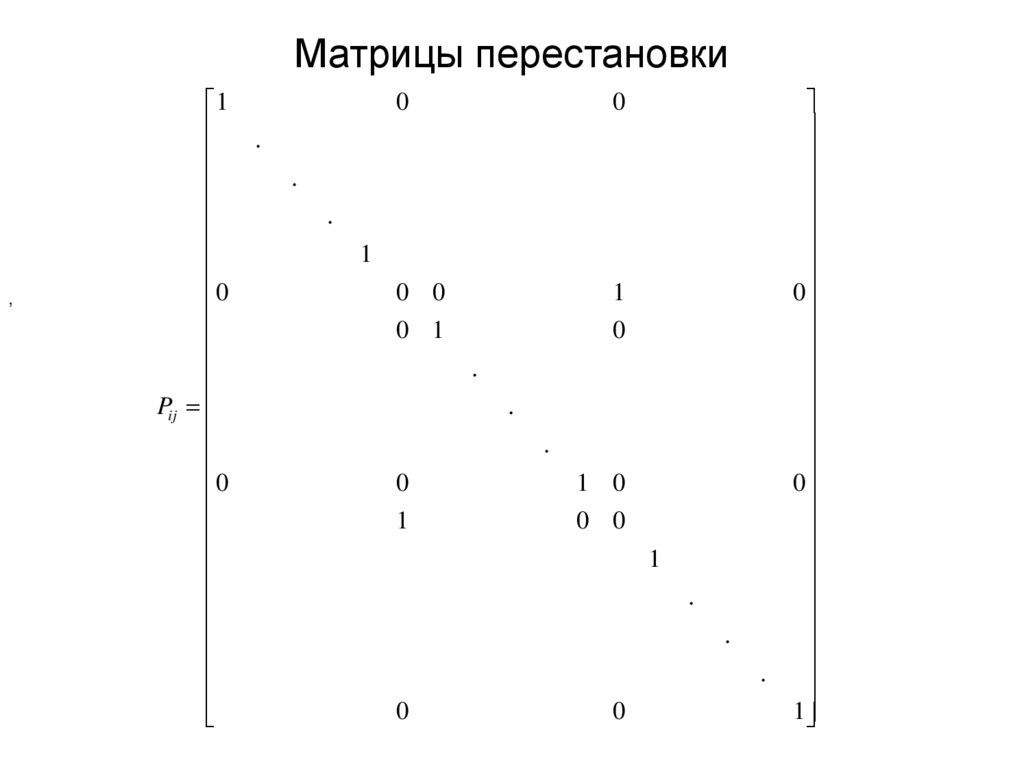
8. Матрицы перестановки

,
1
0
Pij
0
0
0
0 0
1
0 1
0
.
.
.
1
.
.
.
0
1 0
1
0 0
1
.
.
.
0
0
0
0
1

9. Пример матрицы перестановки

0 0 1
P13 0 1 0
1 0 0
21 24 28
A 30 37 42
40 48 55
0 0 1 21 24 28 40 48 55
P13 A 0 1 0 30 37 42 30 37 42
1 0 0 40 48 55 21 24 28
21 24 28 0 0 1 28 24 21
AP13 30 37 42 0 1 0 42 37 30
40 48 55 1 0 0 55 48 40
0 0 1 21 24 28 0 0 1 55 48 40
P13 AP13 0 1 0 30 37 42 0 1 0 42 37 30
1 0 0 40 48 55 1 0 0 28 24 21

10. Матрицы перестановки

0
.
.
0
1
0
.
uij
.
0
1
0
.
.
0
0
.
.
0
1
0
.
vij
.
0
1
0
.
.
0
Pij E uijvijT
vijT uij 2
vijT uij 2 1
1
1
1
T
1 vij uij 1 2
Pij Pij 1
Pij PijT
PijT Pij Pij PijT E

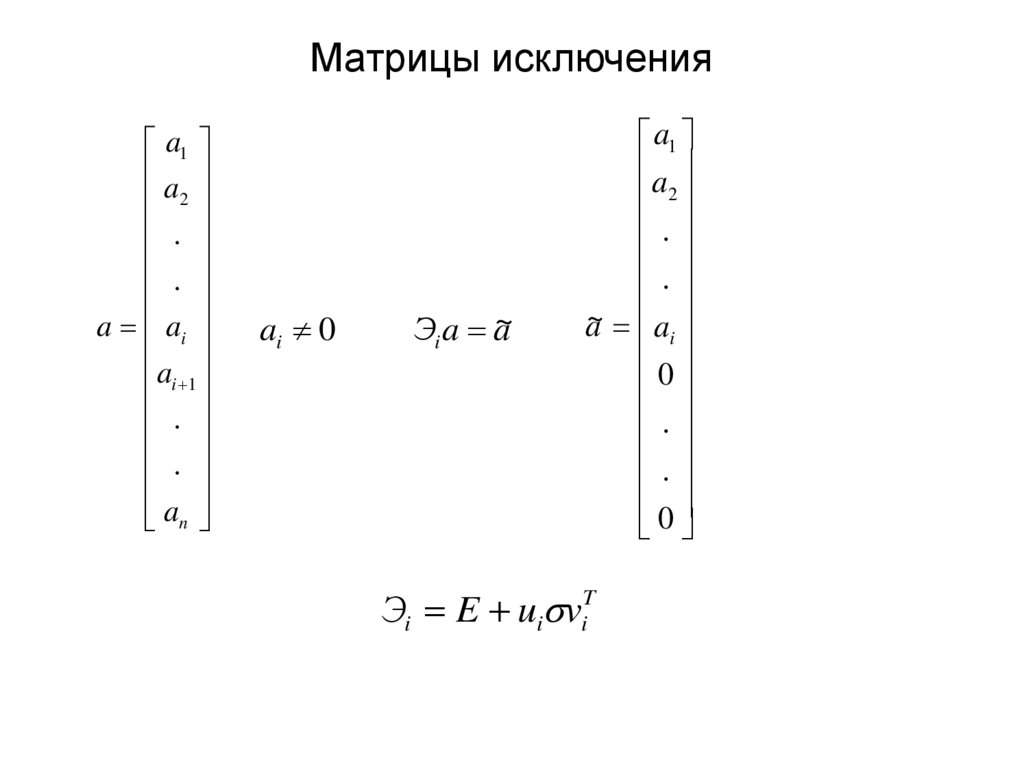
11. Матрицы исключения

a1
a
2
.
.
a ai
ai 1
.
.
a
n
ai 0
Эi a a~
a1
a
2
.
.
a~ ai
0
.
.
0
Эi E ui viT

12. Матрицы исключения и обратная к ней

0
.
.
0
ai 1
ui ai
a
i 2
ai
.
.
a
n
ai
0
.
.
0
vi 1 ei
0
.
.
0
Эi E ui viT
viT ui 0
1
viT ui 0 1
1
1
T
1 vi ui 1
Эi 1 E ui viT

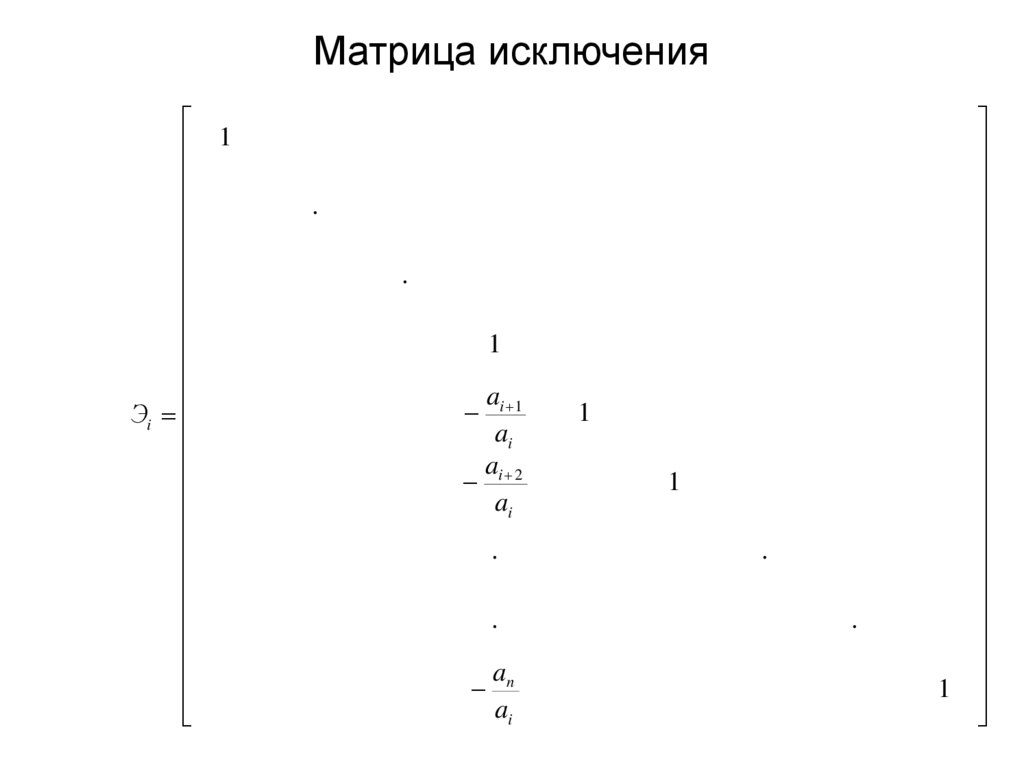
13. Матрица исключения

1
Эi
.
.
1
ai 1
ai
a
i 2
ai
.
.
an
ai
1
1
.
.
1

14. Обратная к матрице исключения

1
Эi 1
.
.
1
ai 1
ai
ai 2
ai
.
.
an
ai
1
1
.
.
1

15. Перемножение матриц исключения Эi и Эк

1
Эi
.
.
1
ai 1
ai
ai 2
ai
.
.
an
ai
1
1
.
.
1
1
Эk
.
.
1
1
1
ak 1
ak
.
an
ak
.
.
1

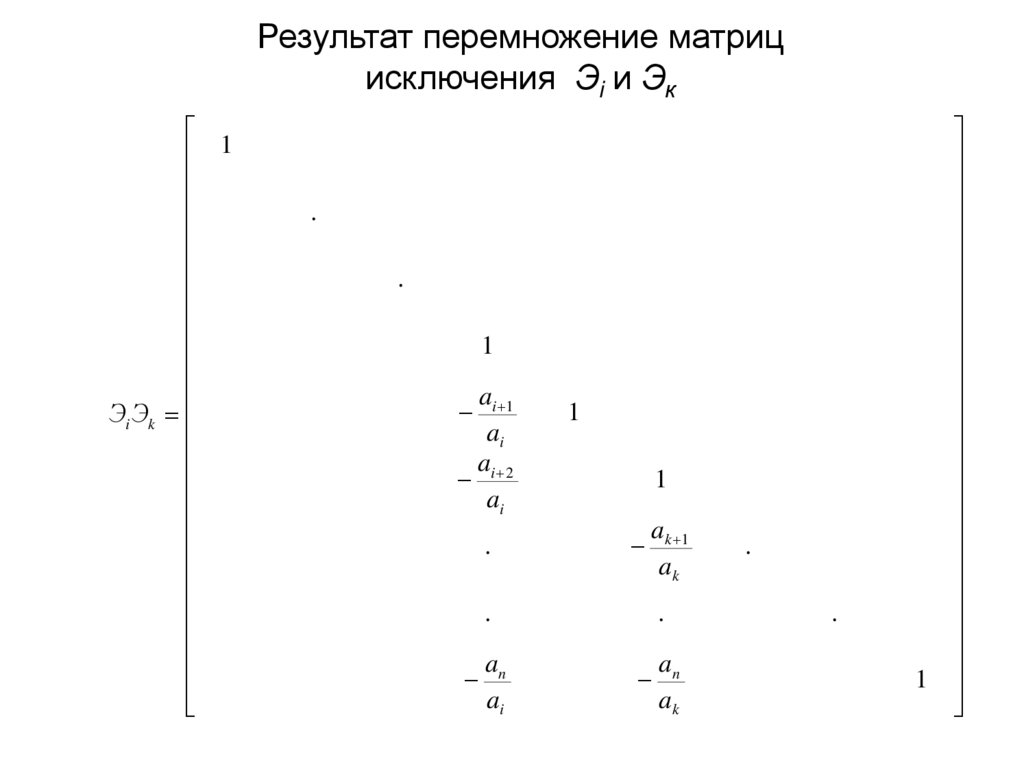
16. Результат перемножение матриц исключения Эi и Эк

1
Эi Эk
.
.
1
ai 1
ai
a
i 2
ai
.
1
1
ak 1
ak
.
an
ai
.
an
ak
.
.
1

17. Матрицы Хаусхолдера

Э E u vT
u v
H E
2
2
u2
2
T
uu
2
u2
u ~
H E 2u~u~T , u~
, u 2 1
u2

18. Свойства матрицы Хаусхолдера

2
H E
u 2 u, u u T u
2
T
uu
2
u2
vT u u T u
H
1
E
2
2
T
2
u2
T
uu
2
u2
u 2 2 1
2
2
2
1 vT u 1 2
H H 1
H HT
2
2
2 T T T
2
T
T
T T
H E 2 uu
E 2 uu
E 2 u u E 2 uu T
u
u2
u2
u2
2
T
HTH E

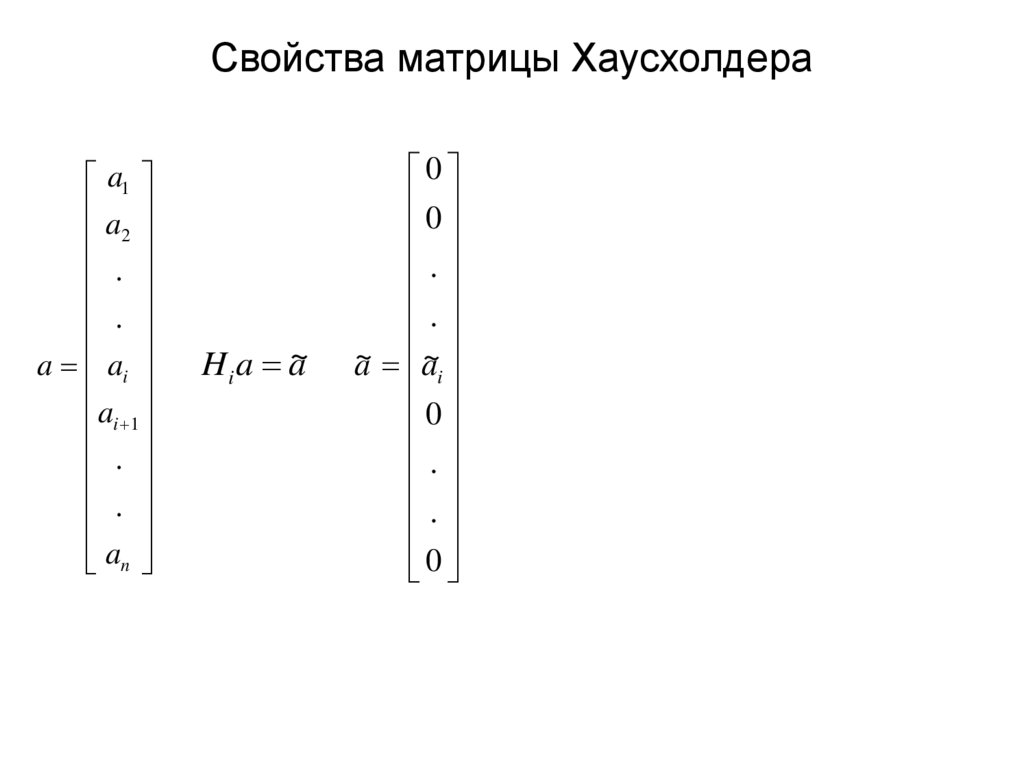
19. Свойства матрицы Хаусхолдера

a1
a
2
.
.
a ai
ai 1
.
.
a
n
H i a a~
0
0
.
.
a~ a~i
0
.
.
0

20. Свойства матрицы Хаусхолдера

Hi E
2
2
ui 2
uiuiT
Hi a a 2 ei
ui a a 2 ei
Hia a
2
ui 2
uu a a
T
i i
2uiT a
2
ui 2
ui
a a e a a e a a e
ui 2 a a 2 ei
2
2
T
T
2 i
T
2 i
2 i i
ui 2 aT a 2 eiT a a 2 ei aT a a 2 eiT a aT a 2 ei a 2 eiT a 2 ei
2
ui 2 2 a 2 2 a 2 ai
2
2
uiT a a a 2 ei a aT a a 2 eiT a a 2 a 2 ai
a
T
2uiT a
2
ui 2
2
ui a ui a a a 2 ei a 2 ei
Hi a a 2 ei

21. Свойства матрицы Хаусхолдера

О выборе знака в ui a a 2 ei
ui a a 2 ei , если ai 0
ui a a 2 ei , если ai 0
z Hy y
2
T
uu
y y
2
2u T y
u2
u
только вектор u
u
~ n операций для
Hy
2
2
2
2
u

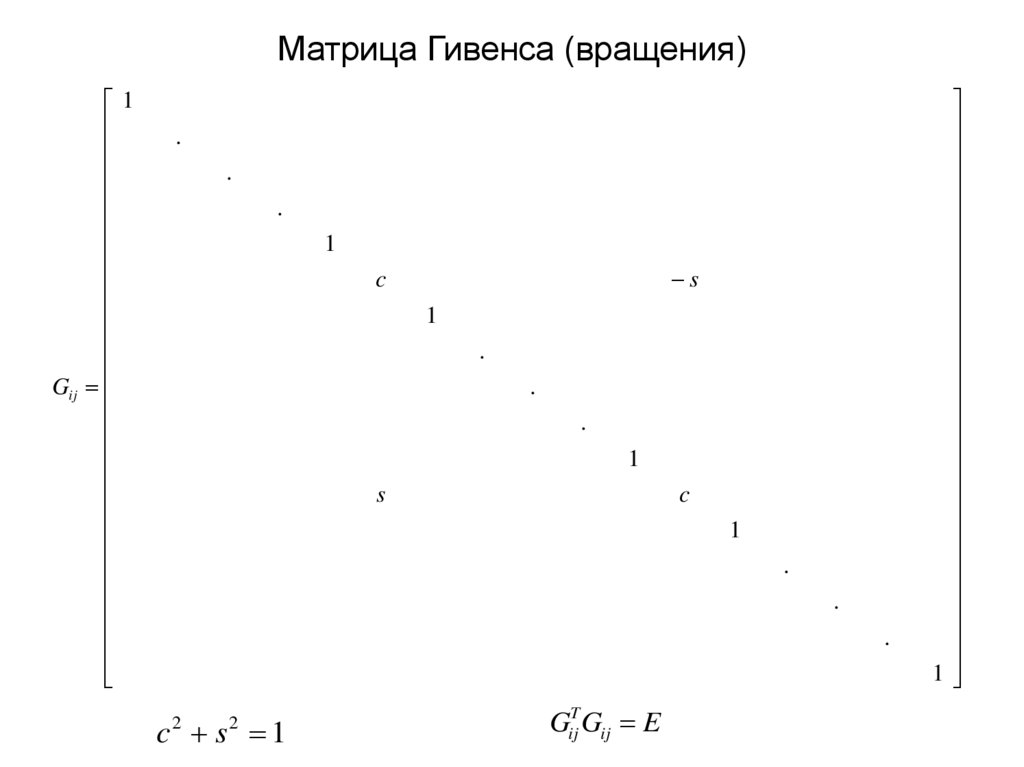
22. Матрица Гивенса (вращения)

1
Gij
.
.
.
1
s
c
1
.
.
.
1
s
c
1
.
.
.
c s 1
2
2
GijT Gij E
1

23. Матрица Гивенса (вращения)

a1
a
2
.
.
a ai
.
a
j
.
a
n
aj 0
Gij a a 2 a~ 2
2
Gij a a~
a1
a
2
.
.
a~ a~i
.
0
.
a
n
a~i ai2 a2j

24. Матрица Гивенса (вращения)

a1
a
2
.
.
Gij a cai sa j
.
sa ca
j
i
.
a
n
cai sa j ai2 a 2j
sai ca j 0
c
s
ai
ai2 a 2j
aj
ai2 a 2j

25. Выполнение операций с матрицей Гивенса (вращения)

y1
y
2
.
.
z Gij y cyi sy j
.
sy cy
j
i
.
a
n
только 4 числа i, j , c, s
или 3 числа i, j , c
6 операций вместо n2 для общего случая

26. Пример для матрицы Хаусхолдера

a1
a
a 2
a3
a4
a~1
0
a~
0
0
a1
1 a1 a 2
a
0
a
2
u 2 a 2
a3
0 a3
a
0
a
4
4
H E
2
u
T
u
u
2
2
Ha a 2 e1 a~

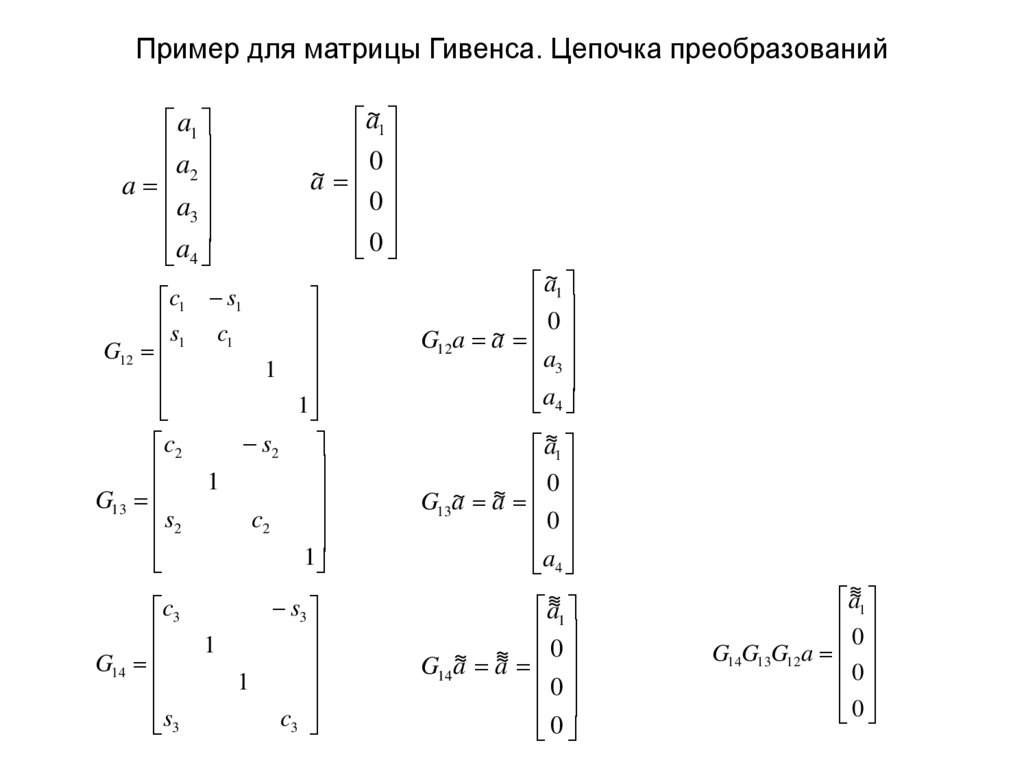
27. Пример для матрицы Гивенса. Цепочка преобразований

a1
a
a 2
a3
a4
a~1
0
a~
0
0
c1 s1
s
c
1
1
G12
1
1
s2
c2
1
G13
s2
c2
1
s3
c3
1
G14
1
s
c
3
3
a~1
0
G12a a~
a3
a4
a~1
0
~
G13a~ a
0
a4
~
a~1
0
~
G14a~ a~
0
0
~
a~1
0
G14G13G12a
0
0