Термодинамика

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительной физики и химии
Физика
Тема
Основы термодинамики
Кирк Яна Геннадьевна
к.п.н., доцент, доцент

2.

2
План лекции
1. Внутренняя энергия
2. Работа идеального газа при изменении объёма. Работа газа в изопроцессах
3. Первое начало термодинамики. Применение первого начала термодинамики к изопроцессам с
идеальным газом
4. Теплоёмкость
5. Адиабатический процесс, уравнение, коэффициент Пуассона
6. Круговой процесс (цикл) КПД цикла
7. Второе начало термодинамики
8. Понятие об обратимых и необратимых процессах
9. Цикл Карно КПД цикла Карно
10. Неравенство Клаузиуса
11. Энтропия
12. Изменение энтропии при изопроцессах с идеальным газом
13. T-S-диаграмма. Доказательство теоремы Карно
14. Термодинамическая вероятность состояния системы (статистический вес)
15. Третье начало термодинамики. Теорема Нернста

3.

Внутренняя энергия
Одно из важных понятий – внутренняя энергия системы U.
Внутренняя энергия тела – это полная энергия тела, за исключением кинетической
энергии движения тела как целого (движения центра масс и вращения тела как целого)
и потенциальной энергии тела во внешних полях
Внутренняя энергия системы – это функция
состояния, то есть однозначно определяется
состоянием системы.
Изменение внутренней энергии системы в какомлибо процессе не зависит от пути перехода, а только
от начального и конечного состояния; а в замкнутом
процессе, когда система возвращается в исходное
состояние, изменение внутренней энергии равно
нулю
3

4.

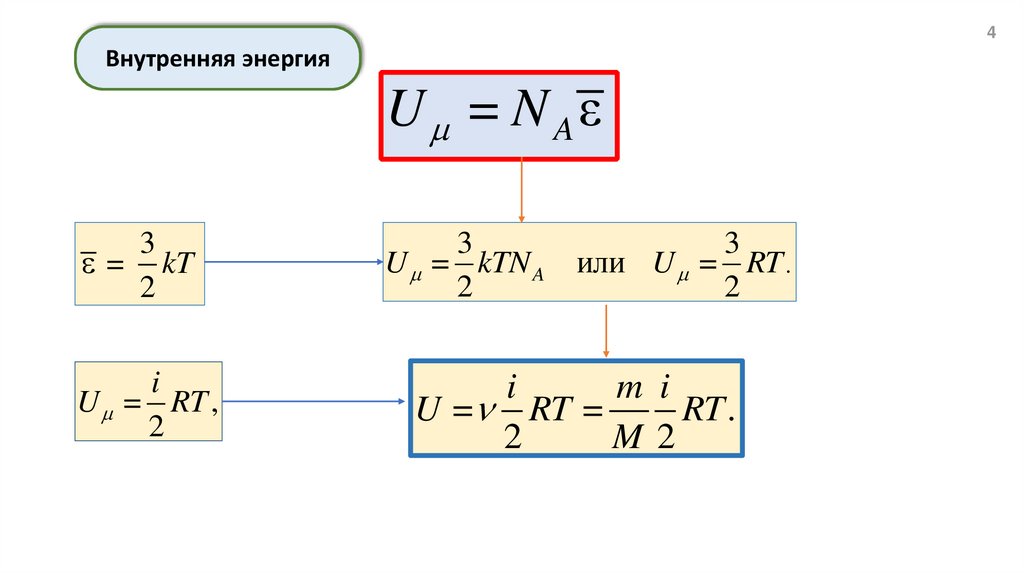
4
Внутренняя энергия
U = N Aε
3
= kT
2
i
U = RT ,
2
3
U = kTN A
2
3
или U = RT .
2
i
m i
U = RT =
RT .
2
M2

5.

Первое начало термодинамики
Внутреннюю энергию системы можно изменить за счёт:
1) совершения над системой работы;
2) сообщения системе теплоты:
dU Q Aвнешних сил
U Q Aвнешних сил
A Aвнешних сил
Q A dU
Q A U
Количество теплоты, сообщённое системе, идёт на
приращение её внутренней энергии и на работу системы
против внешних сил
5

6.

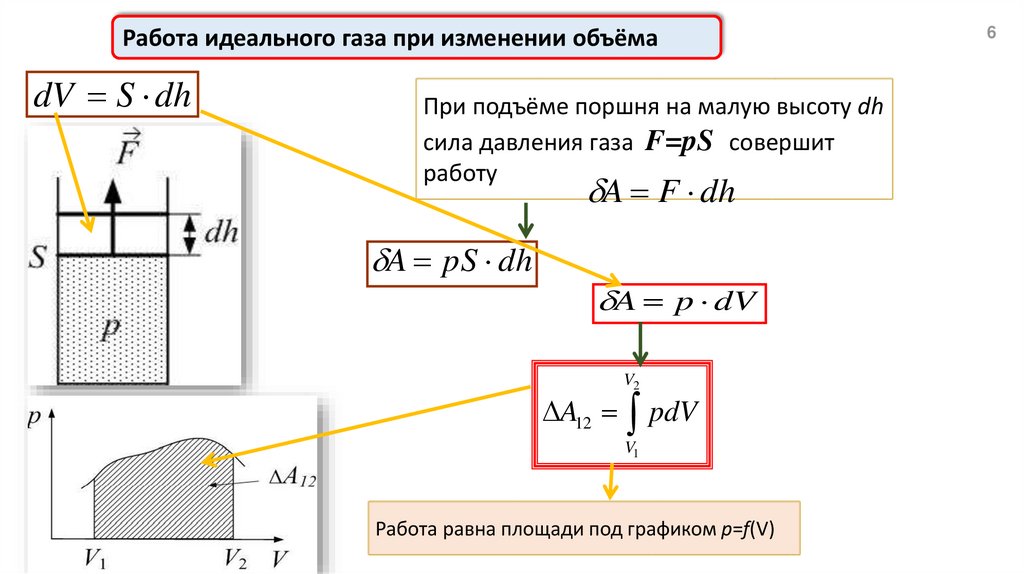
Работа идеального газа при изменении объёма
dV S dh
При подъёме поршня на малую высоту dh
сила давления газа F=pS совершит
работу
A F dh
A pS dh
A p dV
V2
A12 pdV
V1
Работа равна площади под графиком p=f(V)
6

7.

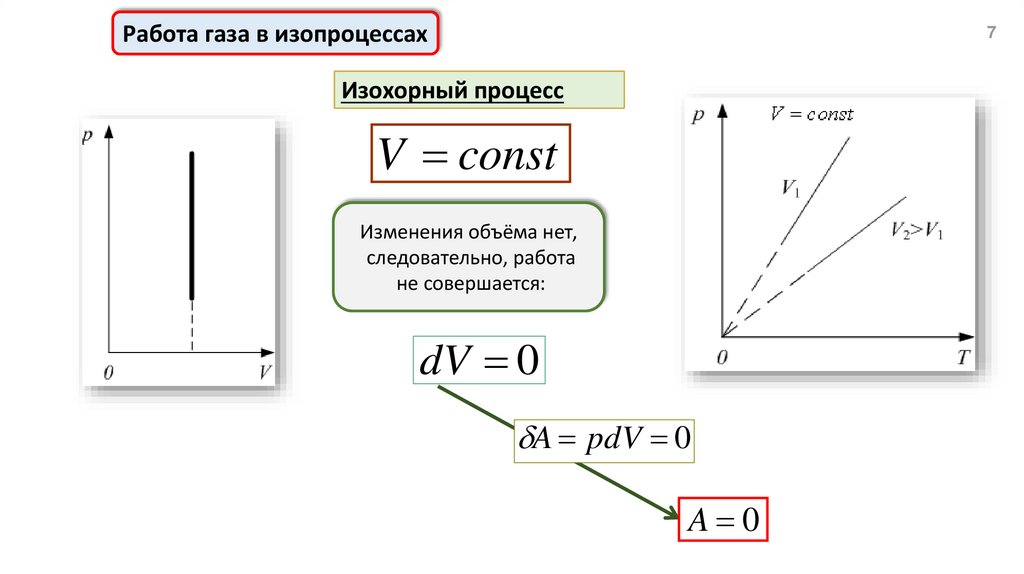
Работа газа в изопроцессах
7
Изохорный процесс
V const
Изменения объёма нет,
следовательно, работа
не совершается:
dV 0
A pdV 0
A 0

8.

Работа газа в изопроцессах
8
Изобарный процесс
V2
V2
V1
V1
A12 pdV p dV p V2 V1
A12 p V
p V1 RT1
p V2 RT2
A12 p V2 V1 pV2 pV1
Универсальная газовая
постоянная R численно
равна работе одного моля
идеального газа при
изобарном нагревании на
1 кельвин
A12 RT2 RT1 R T2 T1
A12 R T
R
A12
T
R
A
dT

9.

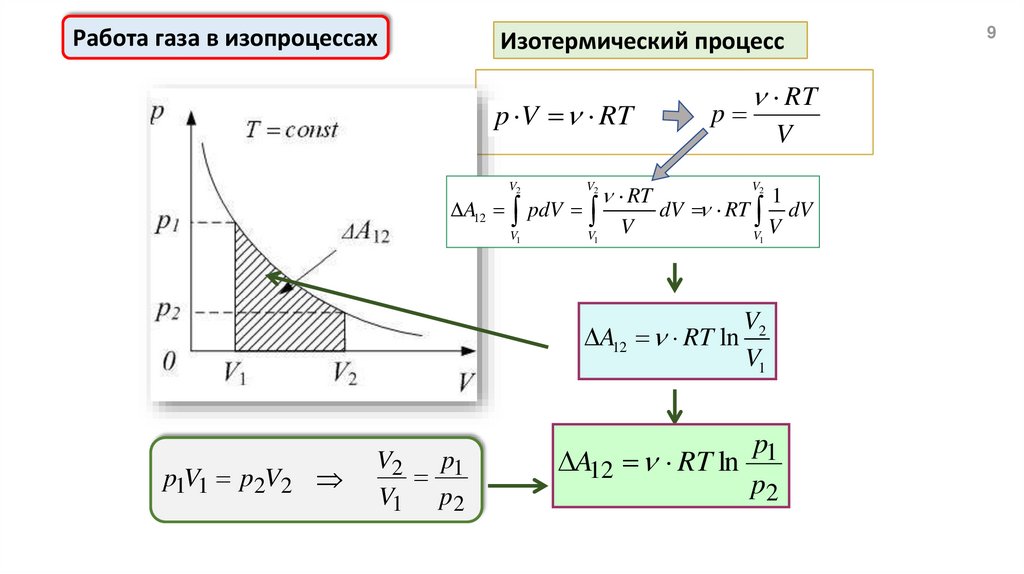
Работа газа в изопроцессах
Изотермический процесс
p V RT
V2
V2
V1
V1
A12 pdV
RT
V
p
RT
V
V2
1
dV
V
V1
dV RT
V2
A12 RT ln
V1
p1V1 p2V2
V2 p1
V1 p2
p1
A12 RT ln
p2
9

10.

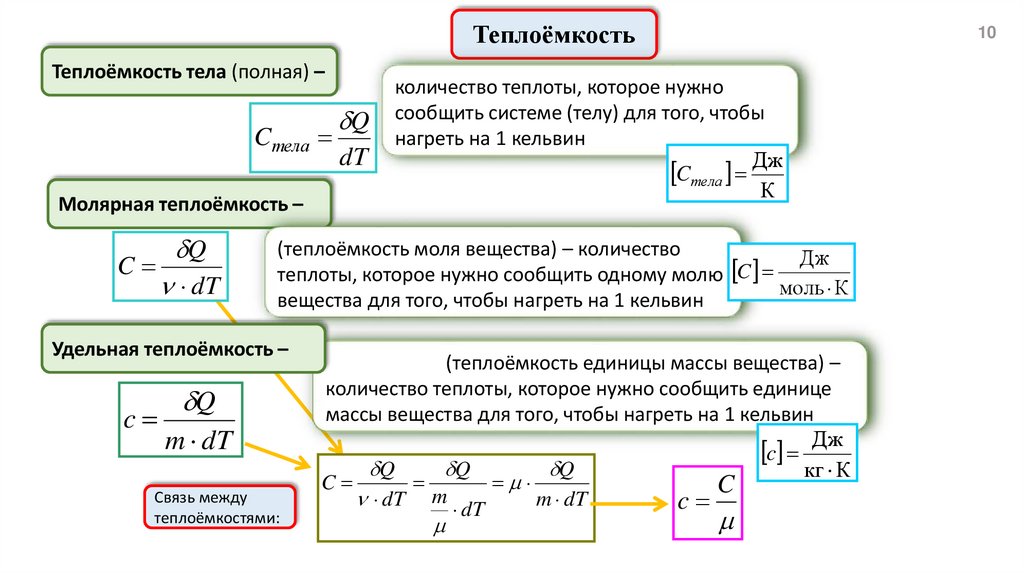
Теплоёмкость
Теплоёмкость тела (полная) –
Cтела
Молярная теплоёмкость –
C
Q
dT
dT
(теплоёмкость моля вещества) – количество
Дж
C
теплоты, которое нужно сообщить одному молю
моль К
вещества для того, чтобы нагреть на 1 кельвин
Удельная теплоёмкость –
c
Q
количество теплоты, которое нужно
сообщить системе (телу) для того, чтобы
нагреть на 1 кельвин
Cтела Дж
К
Q
m dT
Связь между
теплоёмкостями:
(теплоёмкость единицы массы вещества) –
количество теплоты, которое нужно сообщить единице
массы вещества для того, чтобы нагреть на 1 кельвин
c Дж
Q
Q
Q
кг К
C
C
dT m dT
m dT
c
10

11.

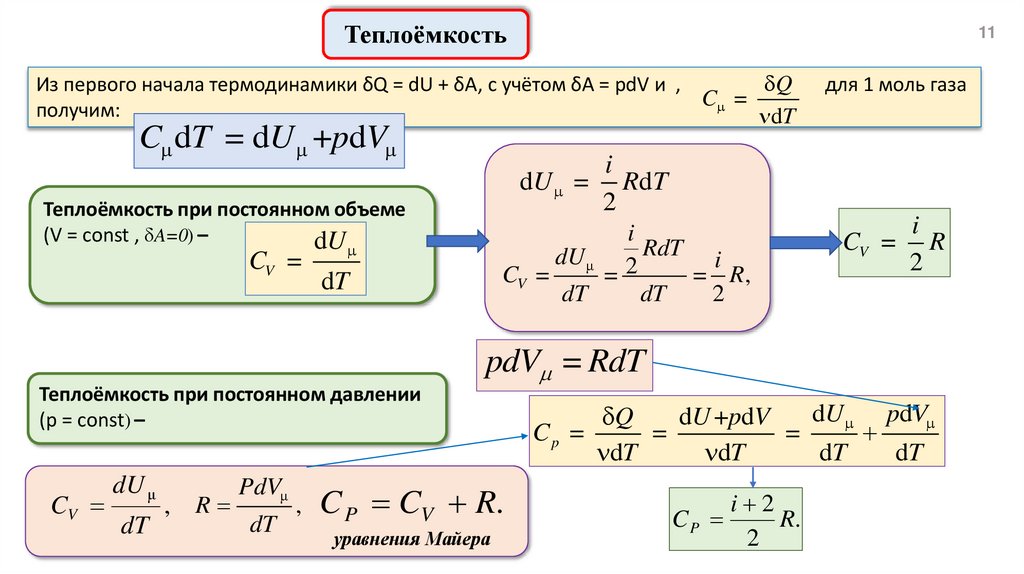
Теплоёмкость
11
Q
Из первого начала термодинамики δQ = dU + δA, с учётом δA = pdV и ,
C =
получим:
dT
C dT = dU +pdV
i
d U = Rd T
2
Теплоёмкость при постоянном объеме
(V = const , δA=0) –
dU
CV =
CV
dU μ
dT
, R
PdVμ
dT
,
i
dU μ 2 RdT i
CV =
=
= R,
dT
dT
2
dT
Теплоёмкость при постоянном давлении
(p = const) –
для 1 моль газа
CV =
i
R
2
pdV = RdT
C P CV R.
уравнения Майера
dU pdV
Q
dU +pdV
Cp =
=
=
dT
dT
dT
dT
i 2
CP
R.
2

12.

Применение первого начала термодинамики к
изопроцессам с идеальным газом
12
Q A dU
1) Изохорный процесс
V const
A 0
Q A dU dU
A 0
Молярная теплоёмкость при постоянном объёме:
dU
U
m
m
CV dT
CV T
Q
m
Q
dU
i
CV
R
dT dT 2
CV dT
Q U
m
CV T2 T1

13.

Применение первого начала термодинамики к изопроцессам с
идеальным газом
p const
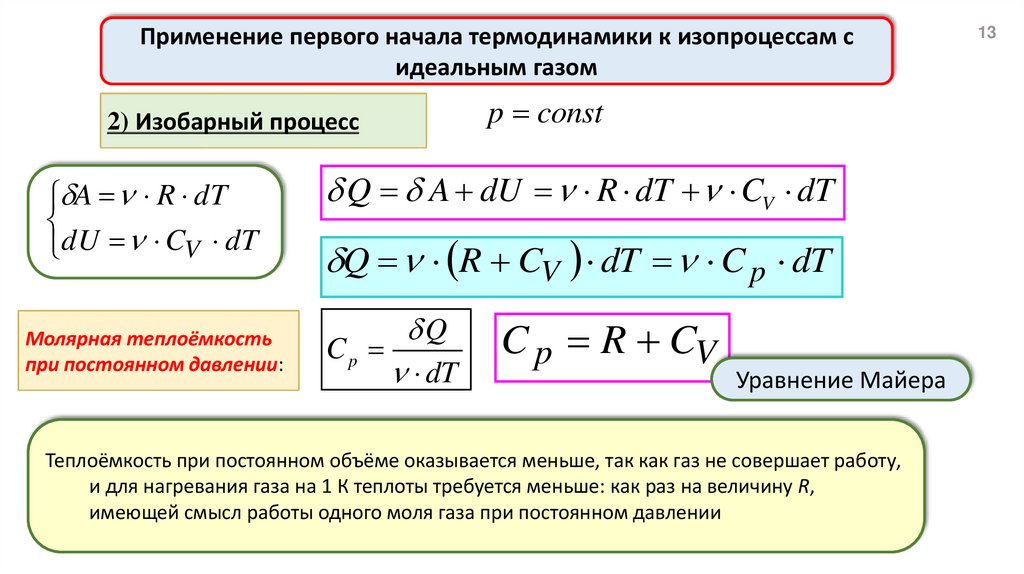
2) Изобарный процесс
A R dT
dU CV dT
Молярная теплоёмкость
при постоянном давлении:
Q A dU R dT CV dT
Q R CV dT C p dT
Cp
Q
dT
C p R CV
Уравнение Майера
Теплоёмкость при постоянном объёме оказывается меньше, так как газ не совершает работу,
и для нагревания газа на 1 К теплоты требуется меньше: как раз на величину R,
имеющей смысл работы одного моля газа при постоянном давлении
13

14.

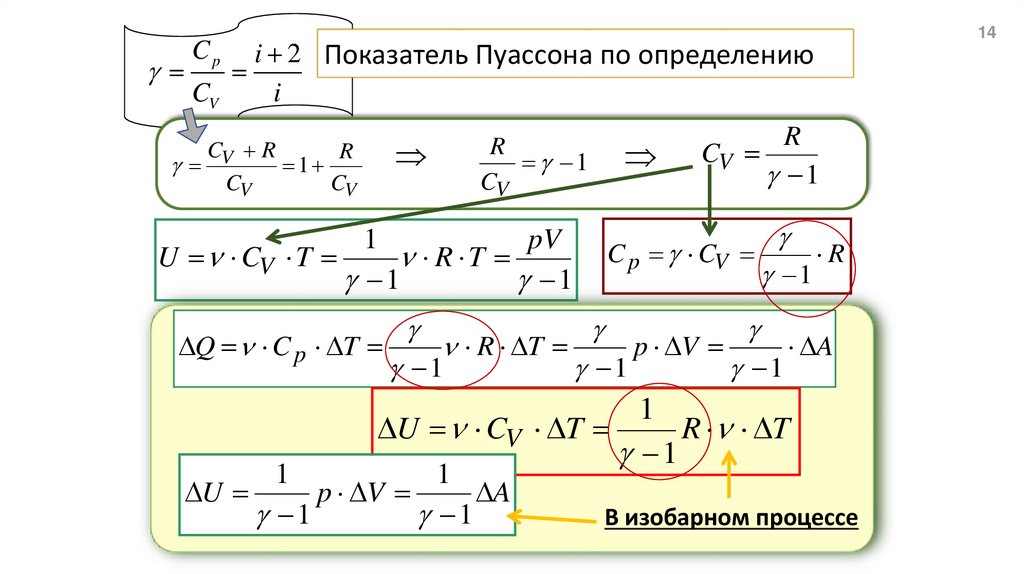
14
i 2 Показатель Пуассона по определению
CV
i
Cp
C R
R
V
1
CV
CV
R
1
CV
1
pV
U CV T
R T
1
1
Q C p T
R T
1
R
CV
1
C p CV
1
p V
1
1
R
A
1
U CV T
R T
1
1
1
U
p V
A
1
1
В изобарном процессе

15.

Cp
CV
i 2
i
Показатель Пуассона
R
CV
1
В изохорном процессе:
R
Q U CV T
T
1
1
Q U
R T2 T1
1
1
RT2 RT1
Q U
1
1
1
p2V p1V
Q U
V p
1
1
15

16.

Применение первого начала термодинамики к
изопроцессам с идеальным газом
3) Изотермический процесс T const
dT 0
dU CV dT 0 U 0
Q A dU A p dV
V2
p1
Q A U A 0 RT ln
RT ln
V1
p2
16

17.

17
4) Адиабатный процесс
протекает без теплообмена с
окружающей средой:
система не получает и не отдаёт теплоты
Q 0
Q 0
Адиабатными процессами будут процессы, протекающие
1) в системе с хорошей теплоизоляцией;
2) очень быстрые процессы, – система не успевает обменяться
теплотой с окружающей средой за время протекания процесса
По первому началу термодинамики:
Q A dU 0
A dU

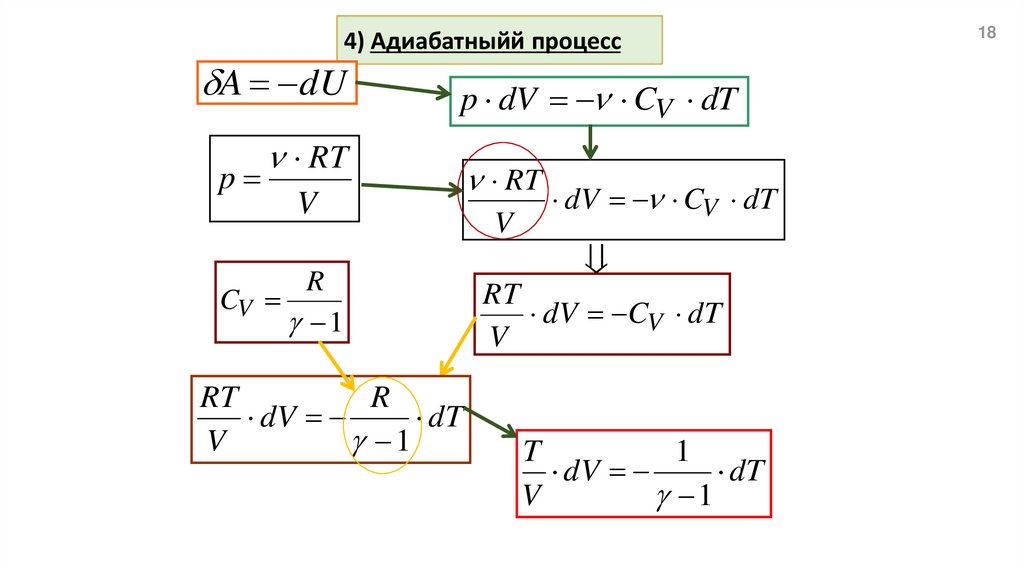
18.

4) Адиабатныйй процесс
A dU
p
p dV CV dT
RT
V
R
CV
1
RT
R
dV
dT
V
1
RT
V
dV CV dT
RT
dV CV dT
V
T
1
dV
dT
V
1
18

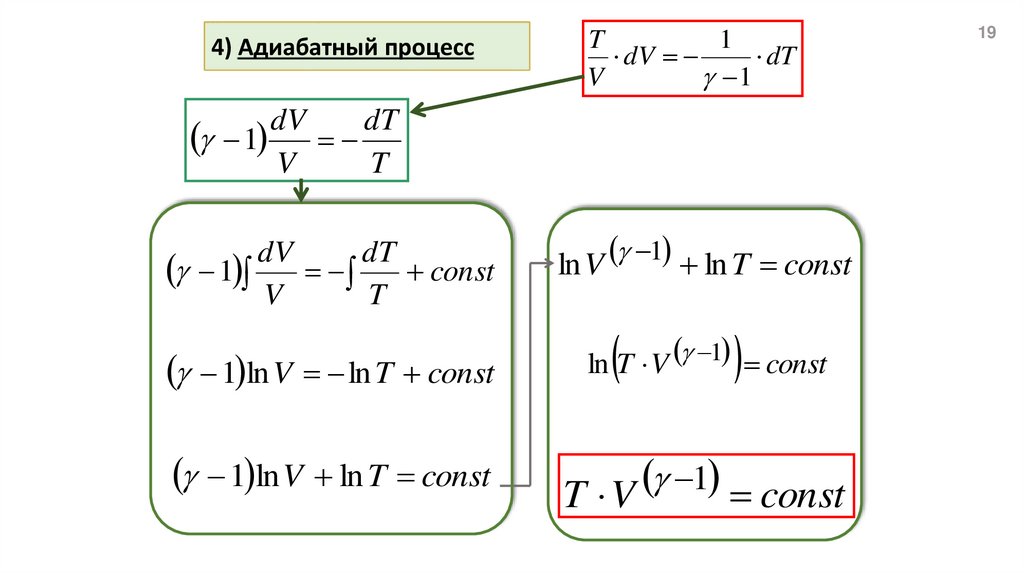
19.

4) Адиабатный процесс
T
1
dV
dT
V
1
dV
dT
1
V
T
dV
dT
1 const
V
T
ln V 1 ln T const
1 ln V ln T const
ln T V 1 const
1 ln V ln T const
1
T V
const
19

20.

4) Адиабатный процесс
T V 1 const
p V
const
T
pV const
p V
const
T
1
T V
const
1 p V
T V
const
T
pV const
p V
p V
T
1
p
const
T const
20

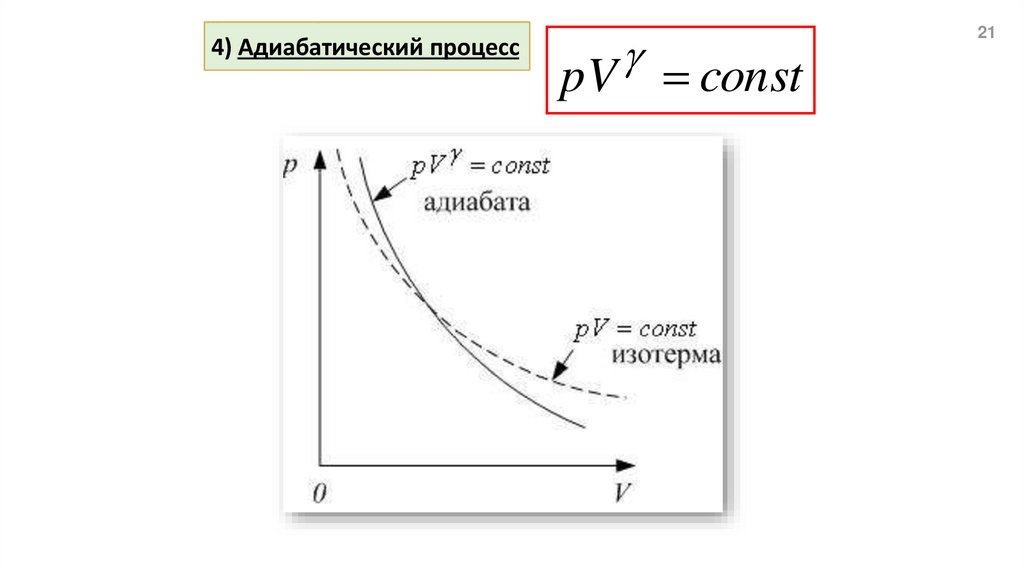
21.

4) Адиабатический процесс
pV const
21

22.

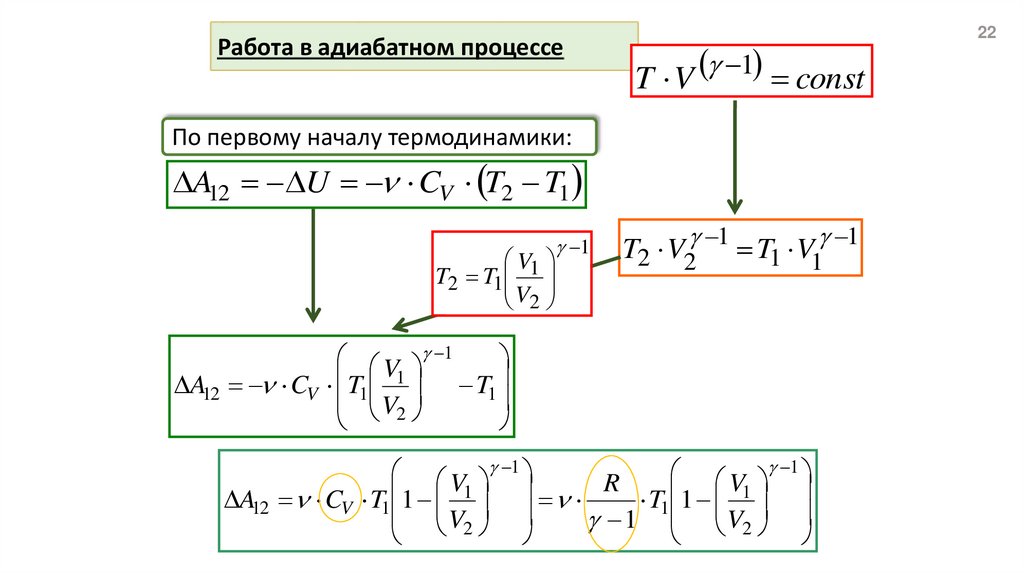
Работа в адиабатном процессе
1
T V
const
По первому началу термодинамики:
A12 U CV T2 T1
V1
T2 T1
V2
1
T2 V2 1 T1 V1 1
V 1
1
A12 CV T1 T1
V2
1
V 1
V1
R
1
A12 CV T1 1
T1 1
V2
1 V2
22

23.

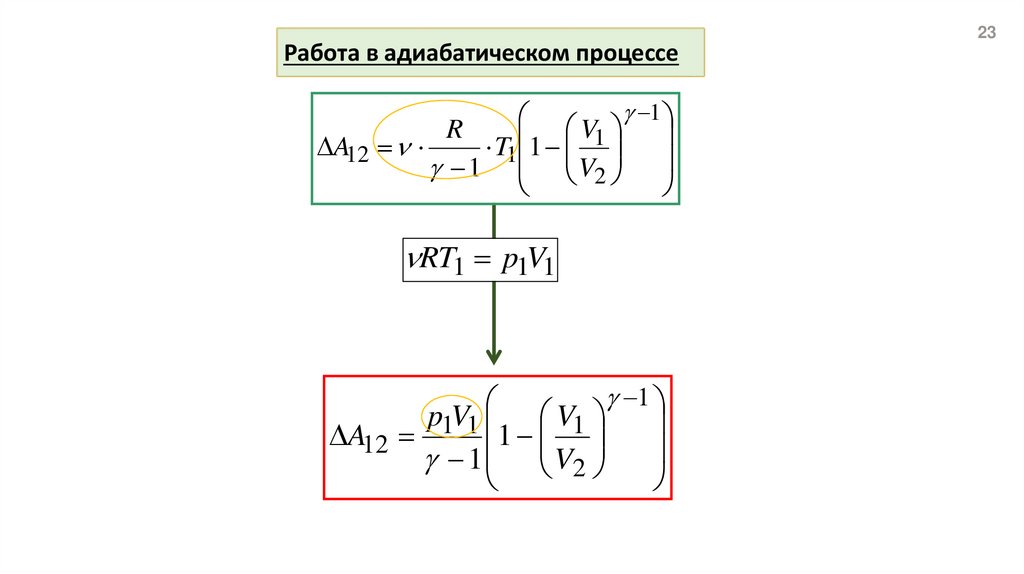
Работа в адиабатическом процессе
1
V1
R
A12
T1 1
1 V2
RT1 p1V1
1
p1V1 V1
A12
1
1 V2
23

24.

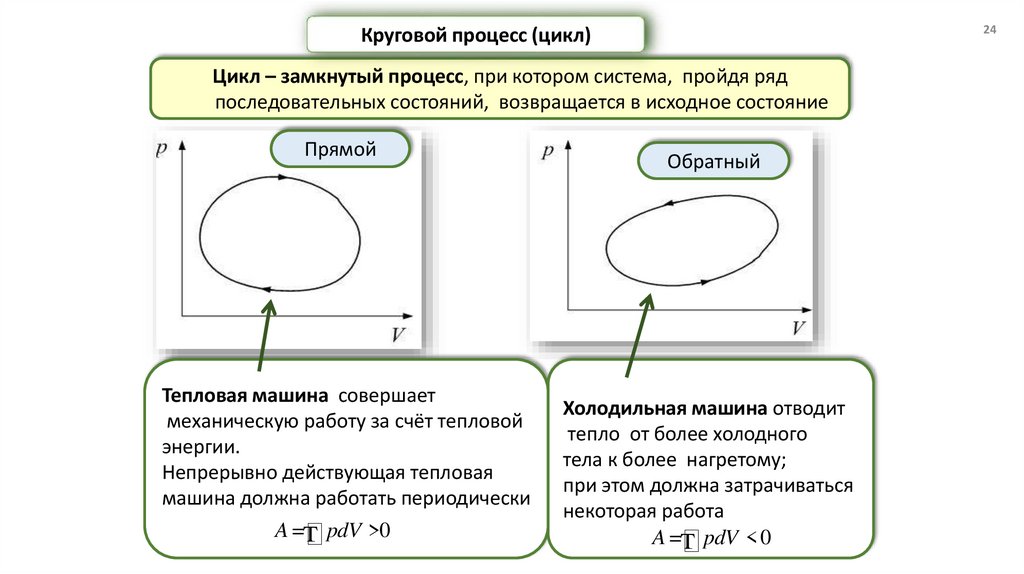
24
Круговой процесс (цикл)
Цикл – замкнутый процесс, при котором система, пройдя ряд
последовательных состояний, возвращается в исходное состояние
Прямой
Тепловая машина совершает
механическую работу за счёт тепловой
энергии.
Непрерывно действующая тепловая
машина должна работать периодически
A =т pdV >0
Обратный
Холодильная машина отводит
тепло от более холодного
тела к более нагретому;
при этом должна затрачиваться
некоторая работа
A =т pdV < 0

25.

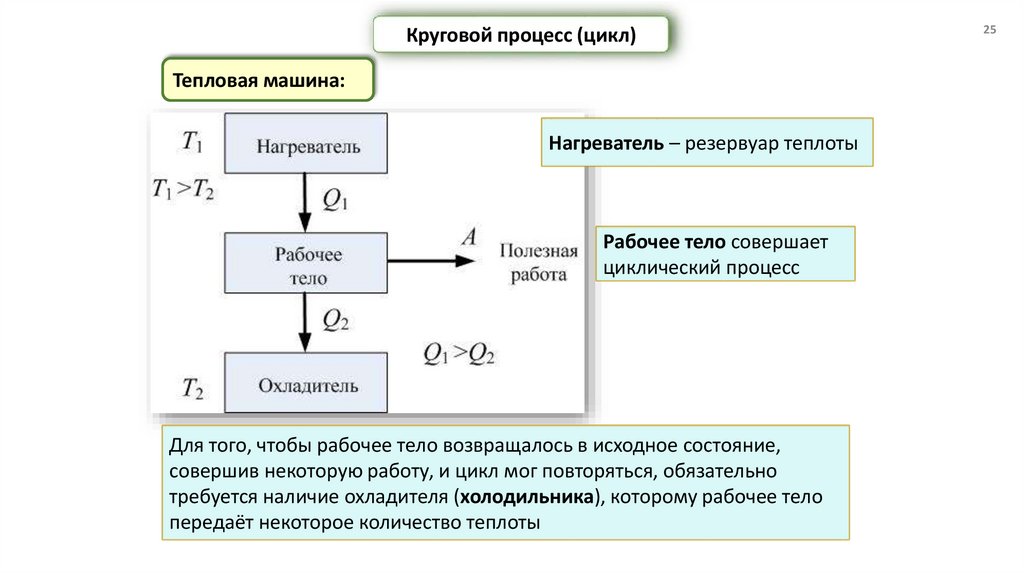
Круговой процесс (цикл)
Тепловая машина:
Нагреватель – резервуар теплоты
Рабочее тело совершает
циклический процесс
Для того, чтобы рабочее тело возвращалось в исходное состояние,
совершив некоторую работу, и цикл мог повторяться, обязательно
требуется наличие охладителя (холодильника), которому рабочее тело
передаёт некоторое количество теплоты
25

26.

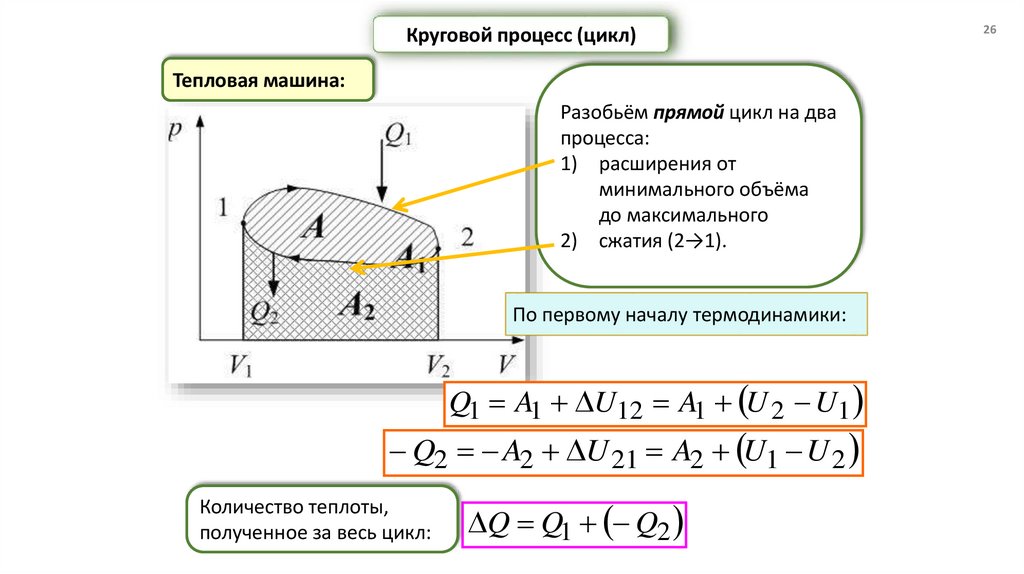
Круговой процесс (цикл)
Тепловая машина:
Разобьём прямой цикл на два
процесса:
1) расширения от
минимального объёма
до максимального
2) сжатия (2→1).
По первому началу термодинамики:
Q1 A1 U12 A1 U 2 U1
Q2 A2 U 21 A2 U1 U 2
Количество теплоты,
полученное за весь цикл:
Q Q1 Q2
26

27.

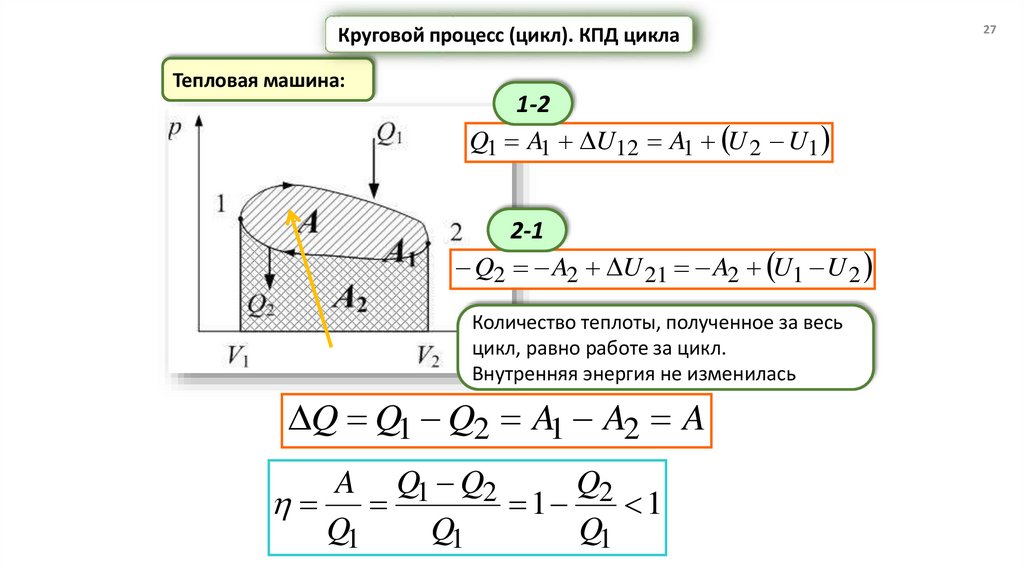
Круговой процесс (цикл). КПД цикла
Тепловая машина:
1-2
Q1 A1 U12 A1 U 2 U1
2-1
Q2 A2 U 21 A2 U1 U 2
Количество теплоты, полученное за весь
цикл, равно работе за цикл.
Внутренняя энергия не изменилась
Q Q1 Q2 A1 A2 A
A Q1 Q2
Q2
1
1
Q1
Q1
Q1
27

28.

Второе начало термодинамики
Опыт показывает, что нельзя построить тепловую машину, которая ВСЮ
полученную от нагревателя теплоту превращает в работу, то есть
машину с КПД=1 (вечный двигатель второго рода)
Формулировка Томсона:
Невозможен вечный
двигатель II рода
Невозможен процесс, единственным результатом которого
является превращение теплоты, полученной от
нагревателя, в эквивалентную ей работу
Формулировка Клаузиуса:
Невозможен процесс, единственным результатом
которого является передача теплоты от более холодного
тела к более нагретому
Теплота сама собой может переходить
только от нагретого к холодному
28

29.

Второе начало термодинамики
Формулировки Томсона и Кельвина эквивалентны
Формулировка Томсона:
Невозможен
двигатель с КПД=1
Формулировка Клаузиуса:
Теплота сама собой может переходить
только от нагретого к холодному
Доказательство:
Если бы теплота Q2 сама собой, без дополнительной работы перешла
от холодильника к нагревателю тепловой машины, то её можно было
бы в конце концов превратить в работу, то есть построить тепловую
машину с КПД=1
29

30.

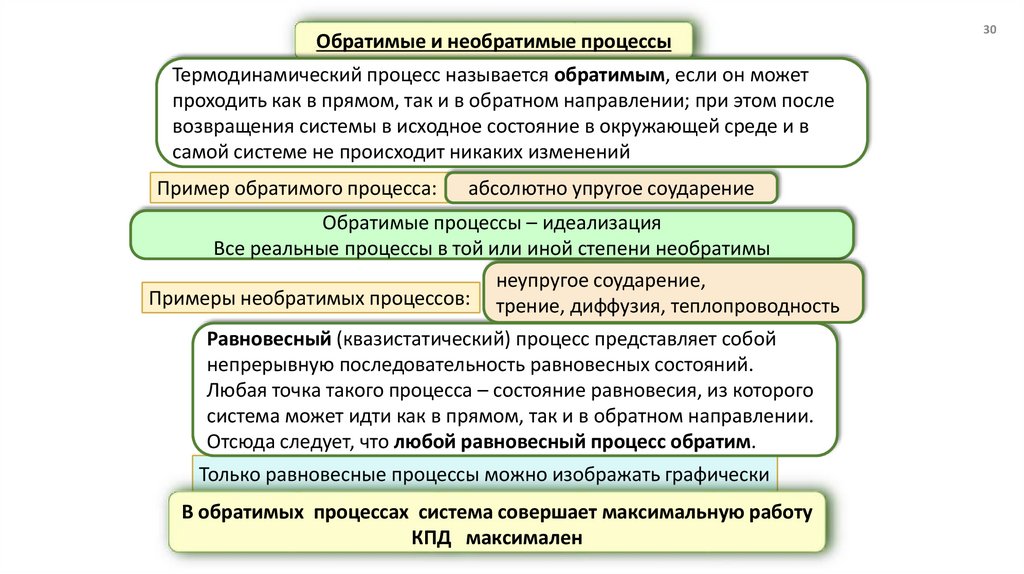
Обратимые и необратимые процессы
Термодинамический процесс называется обратимым, если он может
проходить как в прямом, так и в обратном направлении; при этом после
возвращения системы в исходное состояние в окружающей среде и в
самой системе не происходит никаких изменений
Пример обратимого процесса:
абсолютно упругое соударение
Обратимые процессы – идеализация
Все реальные процессы в той или иной степени необратимы
неупругое соударение,
Примеры необратимых процессов: трение, диффузия, теплопроводность
Равновесный (квазистатический) процесс представляет собой
непрерывную последовательность равновесных состояний.
Любая точка такого процесса – состояние равновесия, из которого
система может идти как в прямом, так и в обратном направлении.
Отсюда следует, что любой равновесный процесс обратим.
Только равновесные процессы можно изображать графически
В обратимых процессах система совершает максимальную работу
КПД максимален
30

31.

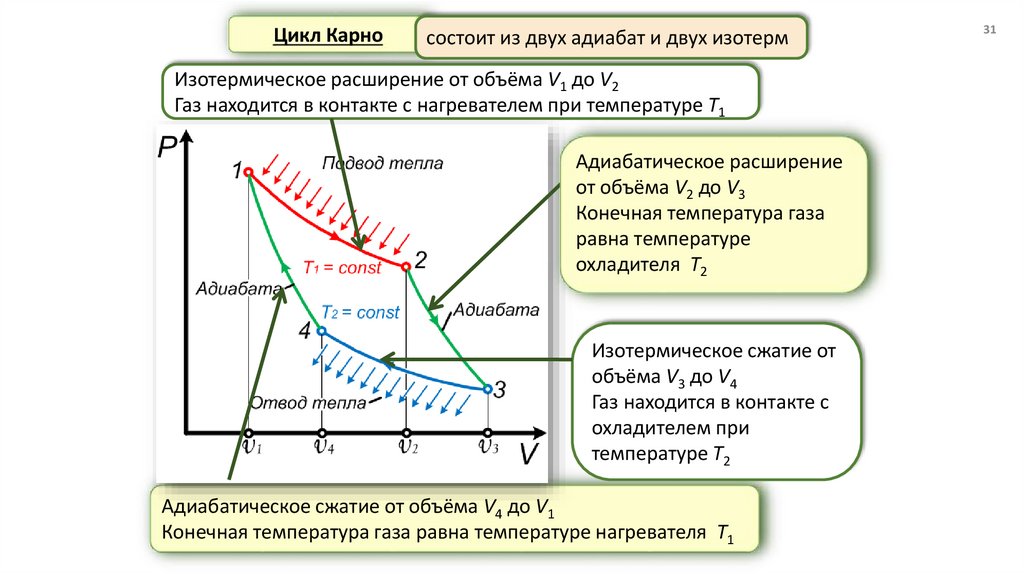
Цикл Карно
состоит из двух адиабат и двух изотерм
Изотермическое расширение от объёма V1 до V2
Газ находится в контакте с нагревателем при температуре T1
Адиабатическое расширение
от объёма V2 до V3
Конечная температура газа
равна температуре
охладителя T2
Изотермическое сжатие от
объёма V3 до V4
Газ находится в контакте с
охладителем при
температуре T2
Адиабатическое сжатие от объёма V4 до V1
Конечная температура газа равна температуре нагревателя T1
31

32.

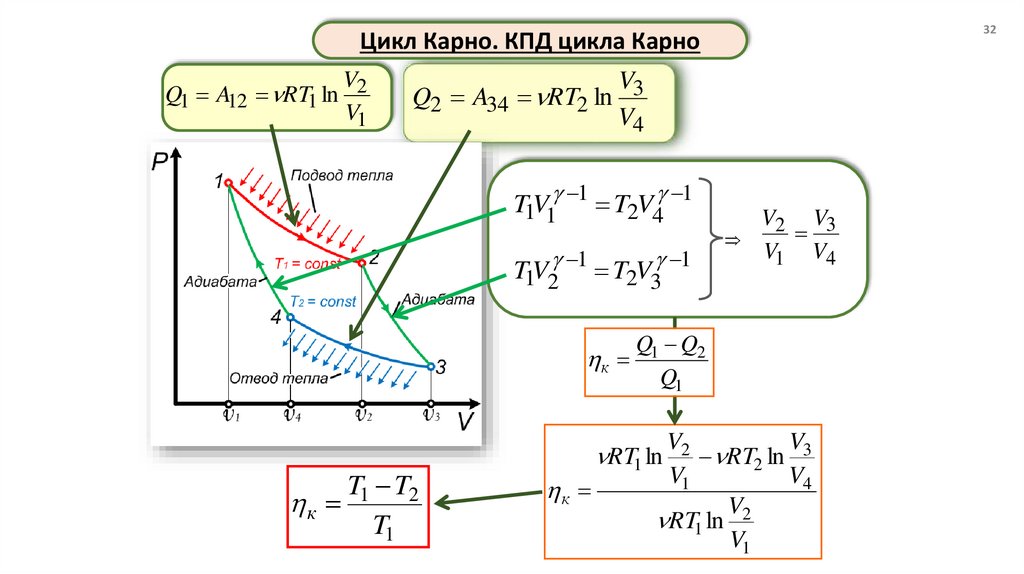
32
Цикл Карно. КПД цикла Карно
V2
Q1 A12 RT1 ln
V1
V3
Q2 A34 RT2 ln
V4
T1V1 1 T2V4 1
T1V2 1 T2V3 1
V2 V3
V1 V4
Q1 Q2
к
Q1
T1 T2
к
T1
к
V2
V
RT2 ln 3
V1
V4
V
RT1 ln 2
V1
RT1 ln

33.

33
Теорема Карно
1) КПД цикла Карно не зависит от природы рабочего тела и
определяется только температурами нагревателя и
охладителя:
T T
к 1
2
T1
2) КПД любого обратимого цикла не больше КПД цикла
Карно с теми же температурами нагревателя и охладителя:
T1 T2
обр. К
T1
3) КПД любого необратимого цикла меньше КПД цикла
Карно с теми же температурами нагревателя и охладителя:
T1 T2
необр. К
T1

34.

Энтропия
34
Понятие энтропии введено Клаузиусом
По определению Клаузиуса, функция состояния системы, дифференциал
которой в обратимом процессе равен отношению теплоты, полученной
системой, к температуре системы , называется энтропией
dS
Q
T
Энтропия – функция состояния системы
Функция состояния – это такая величина, значения которой
однозначно определяются состоянием системы, а изменение функции
состояния при переходе системы из одного состояния в другое
определяется только начальным и конечным состояниями системы и не
зависят от пути перехода
Внутренняя энергия U – тоже функция состояния:
U CV T
U CV T2 T1

35.

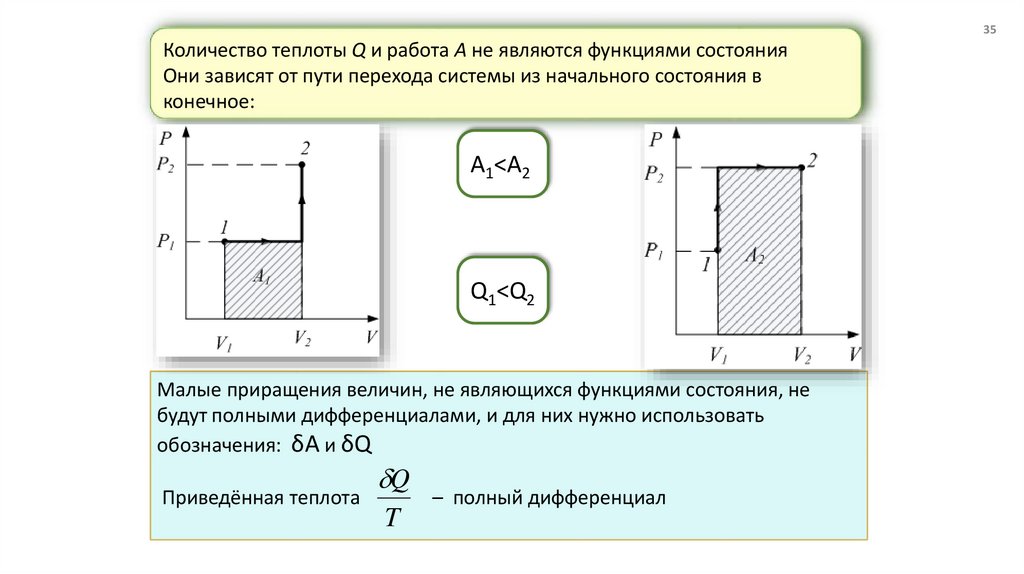
35
Количество теплоты Q и работа A не являются функциями состояния
Они зависят от пути перехода системы из начального состояния в
конечное:
A1<A2
Q1<Q2
Малые приращения величин, не являющихся функциями состояния, не
будут полными дифференциалами, и для них нужно использовать
обозначения: δA и δQ
Q
Приведённая теплота
T
– полный дифференциал

36.

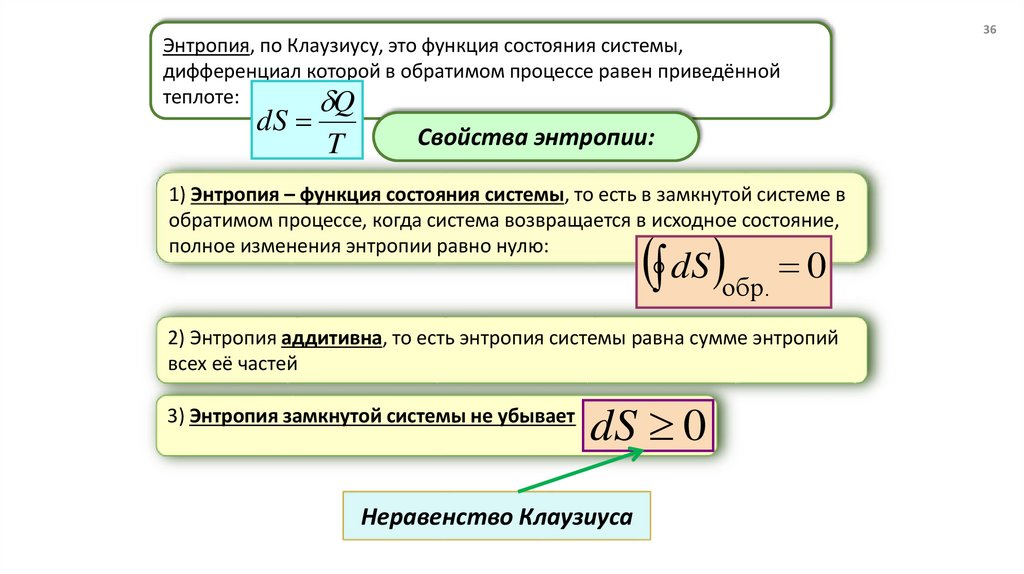
Энтропия, по Клаузиусу, это функция состояния системы,
дифференциал которой в обратимом процессе равен приведённой
теплоте:
Q
dS
T
Свойства энтропии:
1) Энтропия – функция состояния системы, то есть в замкнутой системе в
обратимом процессе, когда система возвращается в исходное состояние,
полное изменения энтропии равно нулю:
dS обр. 0
2) Энтропия аддитивна, то есть энтропия системы равна сумме энтропий
всех её частей
3) Энтропия замкнутой системы не убывает
dS 0
Неравенство Клаузиуса
36

37.

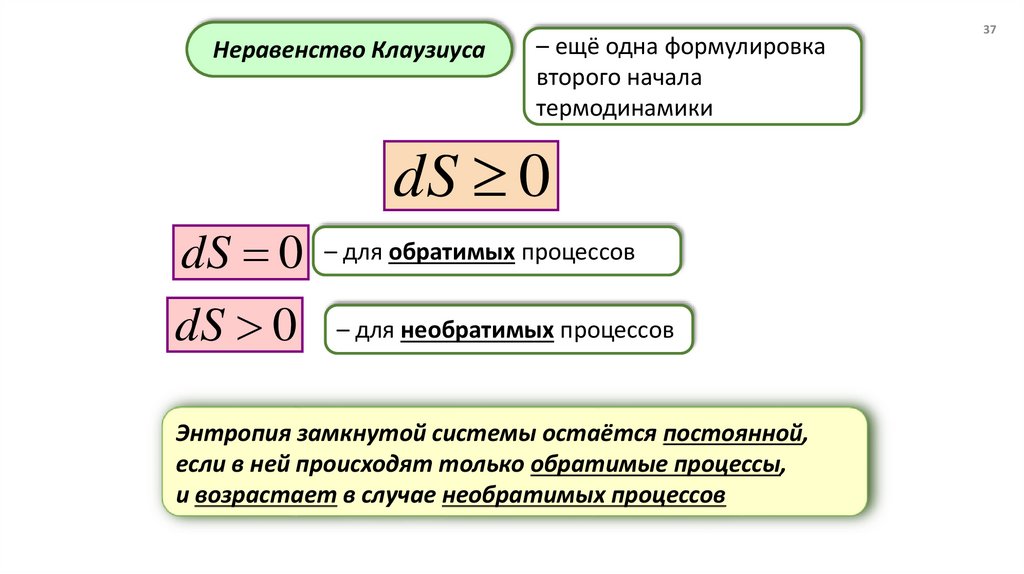
Неравенство Клаузиуса
– ещё одна формулировка
второго начала
термодинамики
dS 0
dS 0 – для обратимых процессов
dS 0
– для необратимых процессов
Энтропия замкнутой системы остаётся постоянной,
если в ней происходят только обратимые процессы,
и возрастает в случае необратимых процессов
37

38.

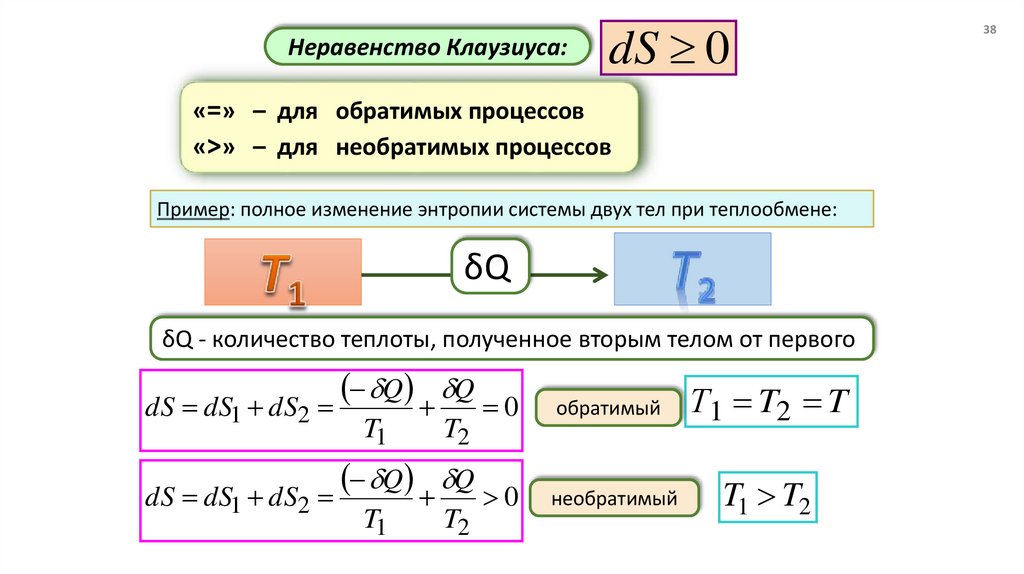
Неравенство Клаузиуса:
dS 0
«=» – для обратимых процессов
«>» – для необратимых процессов
Пример: полное изменение энтропии системы двух тел при теплообмене:
δQ
δQ - количество теплоты, полученное вторым телом от первого
Q Q
dS dS dS
0
обратимый
Т1 T2 T
Q Q
dS dS dS
0
необратимый
T1 T2
1
1
2
2
T1
T1
T2
T2
38

39.

Изменение энтропии при изопроцессах с идеальным газом
dS
Q
Q A dU
T
2
1 Q
2 A dU
S dS
1
1 T
1
T
2 A
1T
P R
T V
V2
S
V1
R dV
V
2 dU
1 T
2 PdV
1 T
2 dU
1 T
dU CV dT
2 C dT
V2
T2
V
R ln
CV ln
T
V1
T1
1
Энтропия увеличивается при расширении газа и при его нагревании
39

40.

Изменение энтропии при изопроцессах с идеальным газом
1) Изохорный процесс V1 V2 T2 P2 S R ln V2 CV ln T2
V1
T1
T1 P1
T
p
S CV ln 2 CV ln 2
T1
p1
2) Изобарный процесс p1 p2 T2 V2
T1
V1 C P CV R
T2
T2
T2
T2
S R ln CV ln R CV ln C p ln
T1
T1
T1
T1
3) Изотермический процесс T1 T2 V2 P1
V1 P2
V2
P1
S R ln
R ln
V1
P2
4) Адиабатный процесс Q 0
dS
Q
T
0
S 0
40

41.

42.

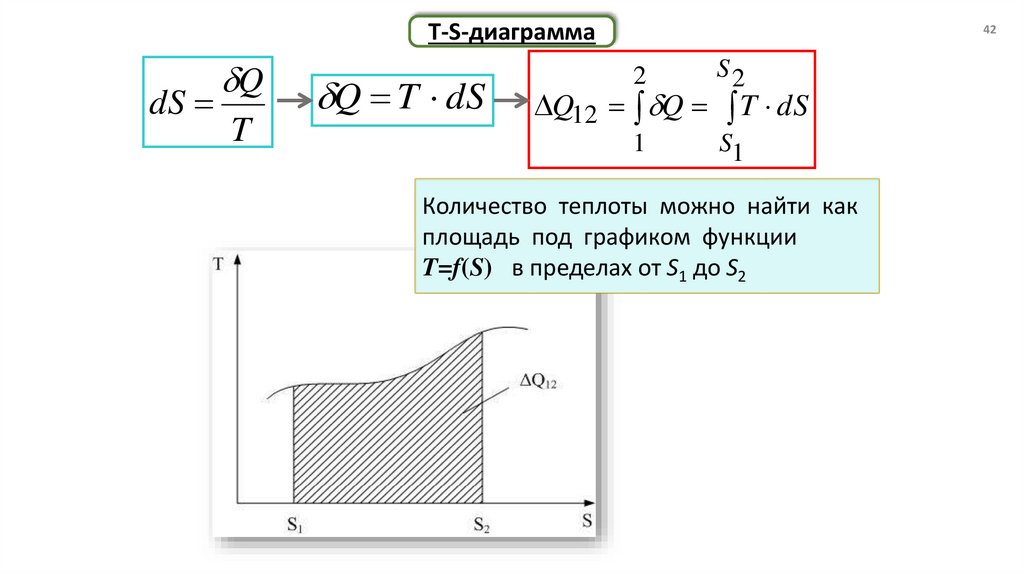
T-S-диаграмма
dS
Q
T
Q T dS
42
2
S2
1
S1
Q12 Q T dS
Количество теплоты можно найти как
площадь под графиком функции
T=f(S) в пределах от S1 до S2

43.

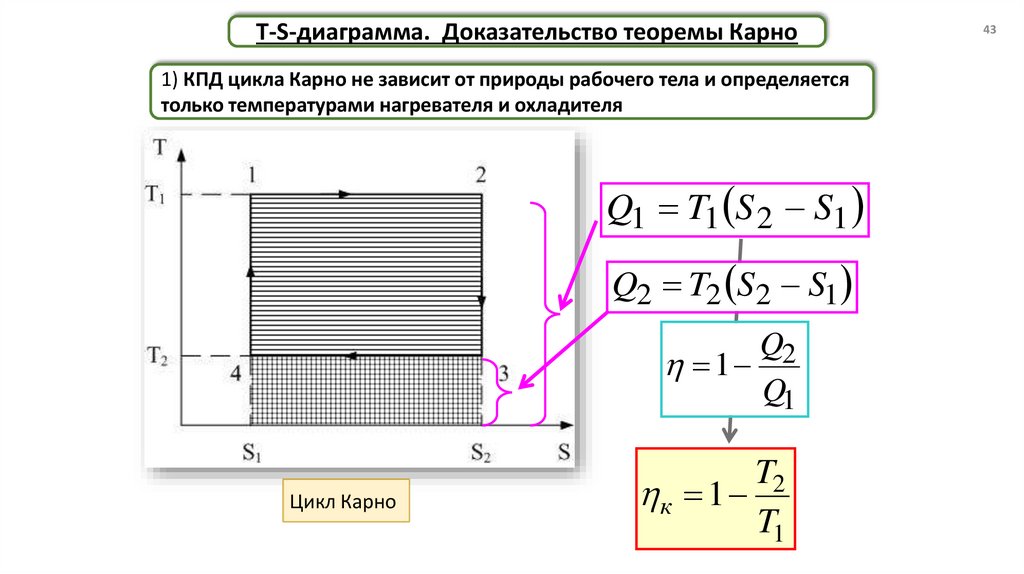
T-S-диаграмма. Доказательство теоремы Карно
1) КПД цикла Карно не зависит от природы рабочего тела и определяется
только температурами нагревателя и охладителя
Q1 T1 S 2 S1
Q2 T2 S2 S1
Q2
1
Q1
Цикл Карно
T2
к 1
T1
43

44.

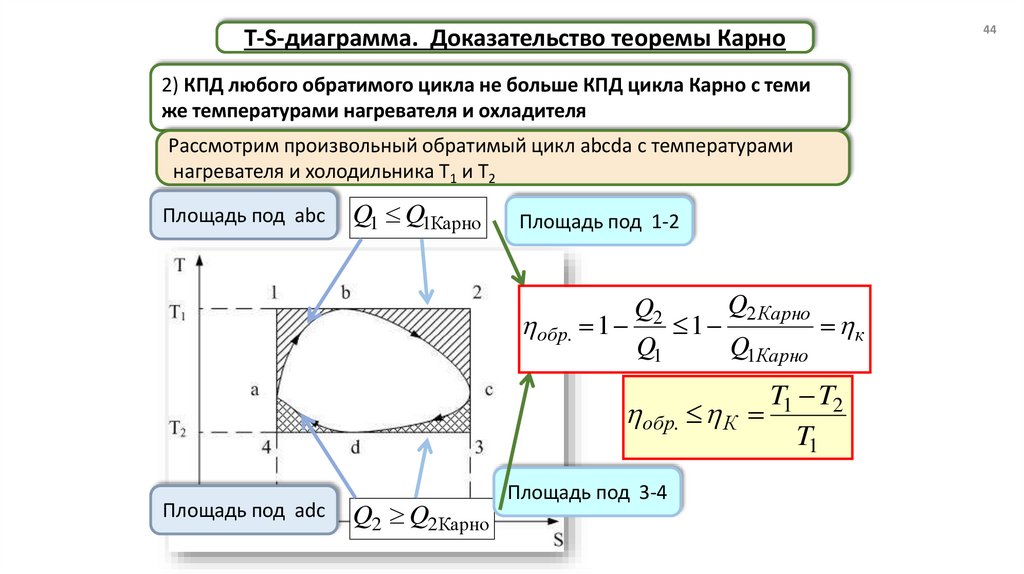
T-S-диаграмма. Доказательство теоремы Карно
2) КПД любого обратимого цикла не больше КПД цикла Карно с теми
же температурами нагревателя и охладителя
Рассмотрим произвольный обратимый цикл abcda с температурами
нагревателя и холодильника Т1 и Т2
Площадь под abc
Q1 Q1Карно
Площадь под 1-2
Q2 Карно
Q2
обр. 1
1
к
Q1
Q1Карно
T1 T2
обр. К
T1
Площадь под adc
Q2 Q2Карно
Площадь под 3-4
44

45.

T-S-диаграмма. Доказательство теоремы Карно
3) КПД любого необратимого цикла меньше КПД цикла
Карно с теми же температурами нагревателя и охладителя
Рассмотрим произвольный обратимый цикл
с температурами нагревателя и холодильника Т1 и Т2
Из-за необратимости максимальная температура рабочего
тела Т1Р.Т. будет меньше Т1, а минимальная Т2Р.Т. – больше Т2:
Т1Р.Т.<Т1
Т2Р.Т. >Т2
Т 2 Р.Т .
Т2
необр. 1
1
К
Т1Р.Т .
Т1
T1 T2
необр. К
T1
45

46.

Термодинамическая вероятность состояния системы
(статистический вес)
Понятие энтропии ввёл Клаузиус, а физический смысл её
выяснил Больцман.
Он предположил, что энтропия связана с
термодинамической вероятностью состояния системы
Определение:
Термодинамическая вероятность (статистический вес)
состояния системы w – число микросостояний
(способов), которыми может быть реализовано данное
макросостояние
46

47.

w – число микросостояний (способов), которыми может быть реализовано
данное макросостояние
Пример 1:
Рассмотрим ящик, содержащий молекулы. Мысленно разделим его пополам. Если
число молекул в ящике равно N=2, то возможны следующие 4 способа разместить
эти две молекулы по двум одинаковым половинам ящика:
Полное число способов
размещения молекул NСП.=4
Термодинамическая вероятность такого состояния, когда обе молекулы
соберутся в одной (например, левой) половине, равна 1: w1=1; это способ №1
Число микросостояний равномерного распределения молекул равно
wРАВН.=2; это способы №3 и 4
Соответствующие математические вероятности:
p1
2
1
p РАВН.
4
4
47

48.

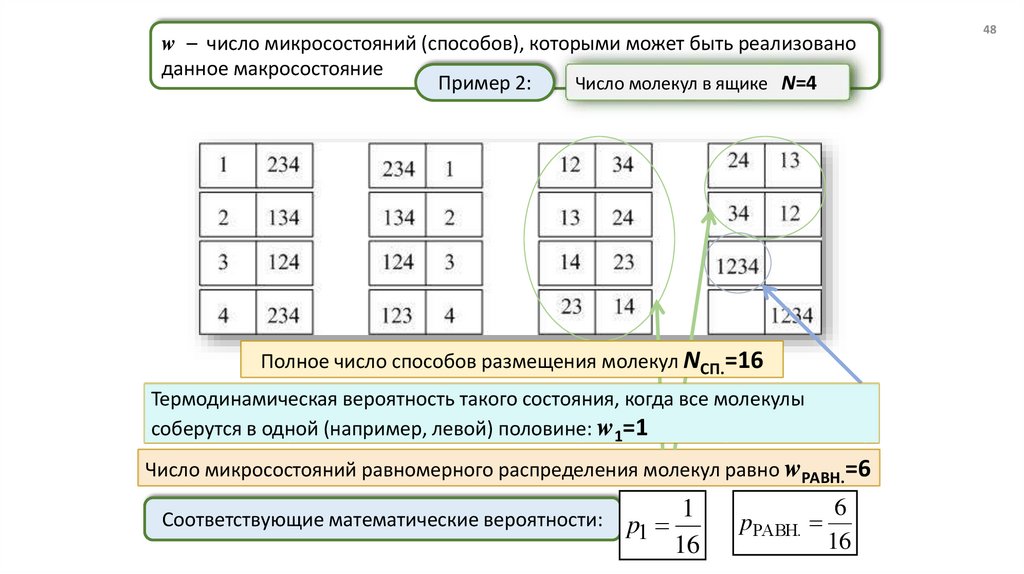
w – число микросостояний (способов), которыми может быть реализовано
данное макросостояние
Число молекул в ящике N=4
Пример 2:
Полное число способов размещения молекул NСП.=16
Термодинамическая вероятность такого состояния, когда все молекулы
соберутся в одной (например, левой) половине: w1=1
Число микросостояний равномерного распределения молекул равно wРАВН.=6
Соответствующие математические вероятности:
1
p1
16
6
pРАВН.
16
48

49.

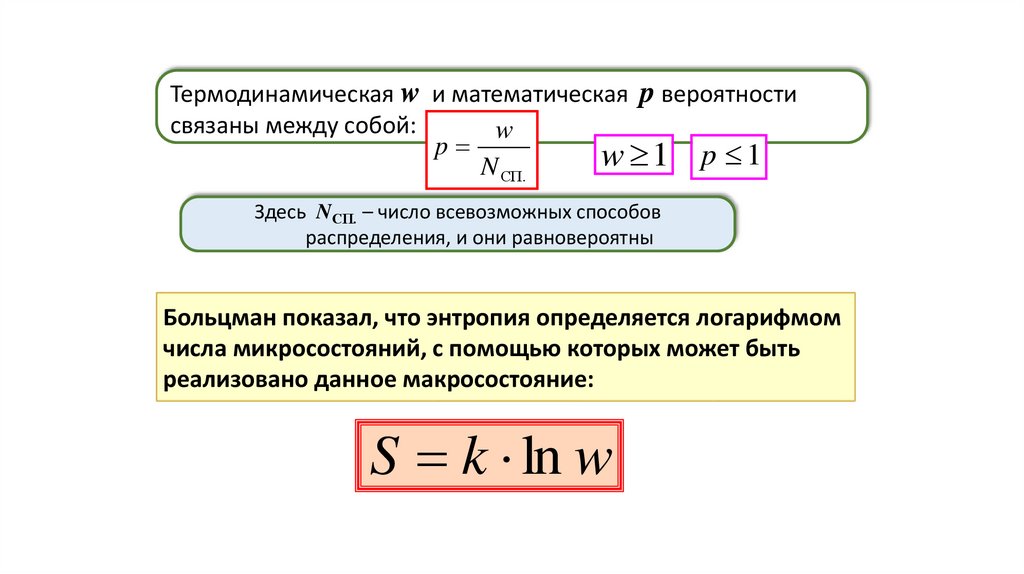
Термодинамическая w и математическая p вероятности
связаны между собой:
w
p
w 1 p 1
N СП.
Здесь NСП. – число всевозможных способов
распределения, и они равновероятны
Больцман показал, что энтропия определяется логарифмом
числа микросостояний, с помощью которых может быть
реализовано данное макросостояние:
S k ln w

50.

Физический смысл энтропии S
Более вероятное состояние оказывается менее
упорядоченным:
для четырёх молекул
w1=1 (более упорядоченное состояние)
wРАВН.=6
Для большого числа молекул разница окажется гораздо
большей:
менее упорядоченное состояние, когда молекулы
распределяются равномерно, имеет существенно большую
термодинамическую вероятность, чем упорядоченное
состояние, когда все молекулы соберутся в одной половине
ящика
Энтропия – мера неупорядоченности
50

51.

Статистический смысл второго начала термодинамики
По второму началу термодинамики,
энтропия изолированных систем не убывает:
S 0
В соответствии с формулой Больцмана S k ln w все реальные
процессы идут в сторону наибольшей термодинамической вероятности;
при обратимых процессах w=const
При малом числе молекул все молекулы могут случайно в какой-то момент
времени в результате теплового движения собраться в одной половине
ящика. Вероятность такого события не мала: p1
1
16
1
p
1
(N=4) и
4 (N=2)
При малом числе молекул в результате флуктуаций статистический вес
состояния может уменьшится. Это происходит потому, что второе начало
термодинамики неприменимо к системам с малым числом частиц
Если молекул в ящике много, вероятность того, что все молекулы в
результате теплового движения в какой-то момент времени соберутся
в одной половине, равна нулю
Второе начало термодинамики – статистический закон,
выражающий закономерности большого числа частиц
51

52.

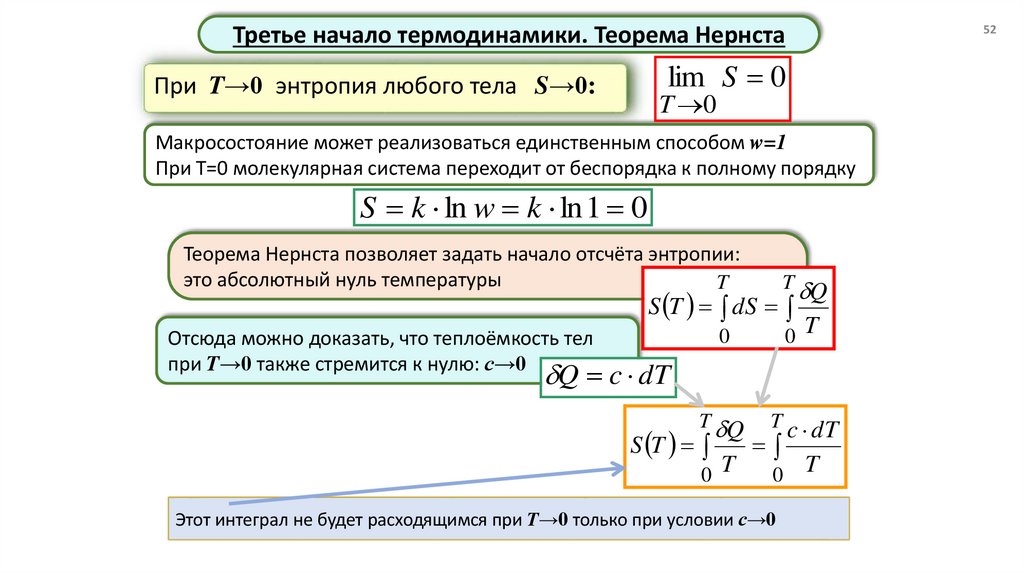
Третье начало термодинамики. Теорема Нернста
52
lim S 0
При T→0 энтропия любого тела S→0:
T 0
Макросостояние может реализоваться единственным способом w=1
При Т=0 молекулярная система переходит от беспорядка к полному порядку
S k ln w k ln 1 0
Теорема Нернста позволяет задать начало отсчёта энтропии:
это абсолютный нуль температуры
T
T Q
S T dS
0
0 T
T Q
T c dT
Отсюда можно доказать, что теплоёмкость тел
при T→0 также стремится к нулю: с→0
Q c dT
S T
0 T
0
Этот интеграл не будет расходящимся при T→0 только при условии с→0
T

53.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительной физики и химии
Авторы:
Кирк Яна Геннадьевна
sfh@spbgasu.ru