lim (4)

1. Границя функції

Границя функції в точці
Односторонні границі
Границя функції на нескінченності
Основні теореми про границі
Обчислення границь
Розкриття невизначеностей
Перша важлива границя

2. Границя функції в точці

Нехай функція y = f(x) визначена в деякому околі точки x0, крім,
можливо самої точки x0.
Число А називається границею функції в точці x0 (або при x x0 ),
якщо для будь-якого ε>0 існує таке число δ>0, що для всіх х із δ –
околу точки x0 виконується нерівність:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x ) A
x x0

3. Границя функції в точці

0; 0; x : x x0 f ( x ) A
ε окіл точки А
y
2
А
0
х0
х
δ окіл точки x0
Геометричний зміст границі: для всіх х із δ – околу точки x0 точки
графіка функції лежать всередині смуги, шириною 2ε, обмеженої
прямими: у = А + ε , у = А - ε .

4. Односторонні границі

В означенні границі функції
lim f ( x ) A
x x0
передбачається, що x прямує до x0 будь-яким способом: може
бути менше, ніж x0 (зліва від x0), більшим, ніж x0 (справа від x0),
або коливається навколо точки x0.
У деяких випадках спосіб наближення аргумента x до x0 суттєво
впливає на значення границі, тому вводять поняття односторонніх
границь.
Число А1 називають границею функції зліва в точці x0, якщо для
будь-якого ε > 0 знайдеться таке δ >0, що для всіх x ( x0 ; x0 )
справедлива нерівність:
f ( x ) A1
Границю зліва записують так:
lim
f
(
x
)
A
1
x x 0
0

5. Односторонні границі

Число А2 називають границею функції справа від точки x0, якщо
0; 0; x x0 ; x0 f ( x ) A2
Границю справа записують так:
Границі функції зліва і справа
називають односторонніми
границями.
y
А2
А1=А2=А
А1
0
lim f ( x ) A2
x x0 0
Очевидно, якщо існує
х0
х
lim f ( x ) A
x x0
то існують і обидві
односторонні границі, причому
А = А1 = А 2

6. Границя функції на нескінченності

Нехай функція y = f(x) визначена на проміжку
; .
x , якщо
Число А називають границею функції при
0; M 0; x : x M f ( x ) A
lim f ( x ) A
x
Геометричний зміст цього
означення такий:
існує таке число М, що
при х > M або при x < - M точки
графіка функції лежать
всередині смуги шириною 2ε,
обмеженої прямими:
у=А+ε,у=А-ε.
y
2
А
0
М
х

7. Основні теореми про границі

Розглянемо теореми, які полегшують знаходження границь
функцій.
Формулювання теорем, коли x x0 або x аналогічні,
тому використовують позначення:
lim f ( x )
Границя суми (різниці) двох функцій дорівнює сумі (різниці)
границь:
lim f1( x ) f2 ( x ) lim f1( x ) limf2 ( x )
Границя добутку двох функцій дорівнює добутку границь :
lim f1( x ) f2 ( x ) lim f1( x ) lim f2 ( x )
Постійний множник можна виносити за знак границі :
lim C f ( x ) C lim f ( x )

8. Основні теореми про границі

Границя дробу дорівнює границі чисельника, поділеній на
границю знаменника, якщо границя знаменника не дорівнює
нулю:
f1( x ) lim f1( x )
lim
f2 ( x ) lim f2 ( x )
lim f ( x ) 0
2
Границя степеня з натуральним показником дорівнює границі у
тій же степені:
lim f ( x ) lim f ( x )
n
n
Границя показниково – степеневої функції:
lim f ( x )
g(x)
lim f ( x )
lim g ( x )

9. Обчислення границь

Обчислення границі:
lim f ( x ) A
x x
0
починають з підстановки граничного значення x0 у функцію f(x).
Якщо при цьому отримують число, то границя дорівнює цьому
числу.
3x 1
3 1 1
lim
2
2
2
x 1
x
1
Якщо при підстановці граничного
значення x0 у функцію f(x) получають
вирази виду:
тоді границя дорівнює:
C
0
C
0

10. Обчислення границь

Часто при підстановці граничного значення x0 у функцію f(x)
получають вирази виду:
0
;
0
; 0 ; 1 ; 0 0 ; 0 ; 0 ;
Ці вирази називають невизначеностями, а обчислення границь
у такому випадку - розкриття невизначеностей.

11. Розкриття невизначеностей

Розкриття невизначеності
0
0
x 2 14 x 32
0
x 2 x 16
lim
lim
2
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Якщо f(x) – дробово –
x 1 1 x 1 1
0
xраціональна
1 1 функція,
необхідно разкласти
на
lim
lim
Якщо f(x) – ірраціональний
x
0
x 0
0 і
x
множники
чисельник
x x домножити
1 1
дріб, необхідно
знаменик дробу
чисельник і знаменик дробу на
x
1 1
1вираз, спряжений
1
до
lim
lim
x 0
x 0
x x 1 1
x 1 чисельника.
1 2

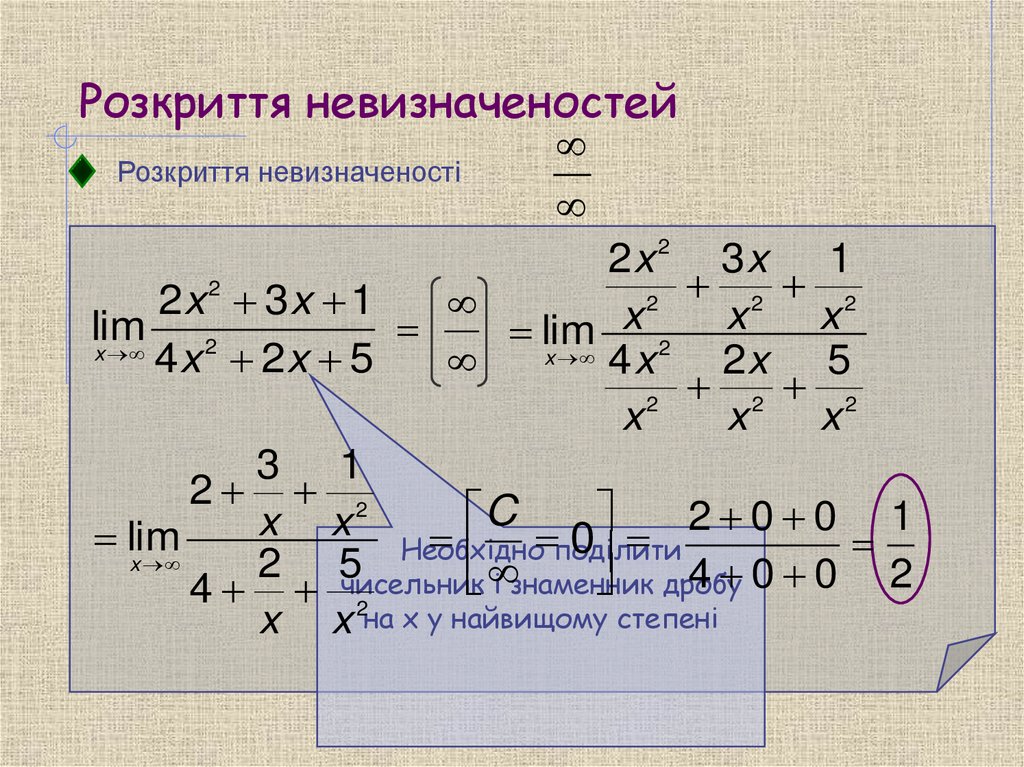
12. Розкриття невизначеностей

Розкриття невизначеності
2
2x
3x 1
2 2
2
2x 2 3 x 1
x
x
x
lim
lim
x
x 4 x 2
4 x 2 2x 5
2x 5
2 2
2
x
x
x
3 1
2 2
C
2 0 0 1
x
x
lim
поділити
0
Необхідно
x
2 5
4 0 0 2
дробу
і знаменник
4 чисельник
x x 2на x у найвищому степені

13. Розкриття невизначеностей

Розкриття невизначеності
2
2
lim
x
1
x
1
x
x 1 x 1 x 1 x 1
lim
x 1 x 1
2
x
2
2
2
2
2
2 Домножимо і поділимо
2
( x 1) ( xфункцію
1) на спряжений вираз
lim
lim
2
2
x
2
2
x
x
1
x
1
x 1 x 1
2
2
0

14. Перша важлива границя

Функція
sin x
x
не визначена при x = 0.
Знайдемо границю цієї функції при
М С
x
О В А
OA 1
x 0
0 x
2
Позначаємо:
S1 - площа трикутника OMA,
S2 - площа сектора OMА,
S3 - площа трикутника OСА,
Із малюнка видно, що S1< S2 < S3
1
1
1
S1 OA MB OA 0M sin x sin x
2
2
2

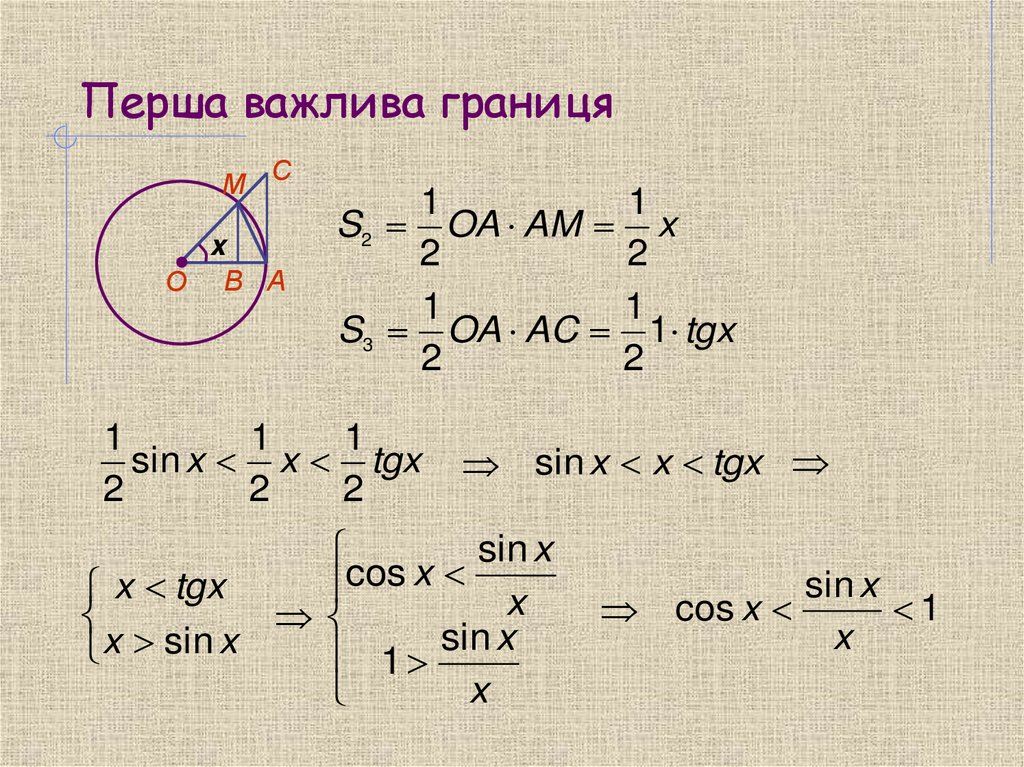
15. Перша важлива границя

М С
x
О В А
1
1
S2 OA AM x
2
2
1
1
S3 OA AC 1 tgx
2
2
1
1
1
sin x x tgx
2
2
2
sin x x tgx
sin x
cos x x
x tgx
sin x
x sin x
1
x
sin x
cos x
1
x

16. Перша важлива границя

sin x
cos x
1
x
lim cos x cos 0 1
x 0
lim1 1
sin x
lim
1
x 0
x
x 0
Формула справедлива також при x < 0
Наслідки:
x
lim
1
x 0
sin x
tgx
lim
1
x 0
x
x
lim
1
x 0
tgx
sin kx
lim
1
x 0
kx

17. Перша важлива границя

0
1 cos 4 x
2 sin 2x
sin 2 x
lim
lim
2 lim
2
2
x 0
x
0
x
0
0
x
x
x
2
2
sin 2 x 2 lim 2 sin 2 x
x 0
2 lim
2x
x 0 x
2
2
sin 2 x
2
2 2 lim
2 2 1 8
x 0
2x
2