Похожие презентации:
17638698589754_кинематика вращательного движения (3)
1.
2.КИНЕМАТИКАВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ
28.01.2026 11:22
1
2.
РАВНОМЕРНОЕ ВРАЩАТЕЛЬНОЕДВИЖЕНИЕ
o
При движении тела по окружности с
постоянной по величине скоростью υ говорят,
что
оно
совершает
равномерное
вращательное движение.
Тело, совершающее равномерное вращательное движение, ускоряется.
3.
где- изменение скорости за малый промежуток времени,
если t стремится к нулю, то имеем дело с мгновенным ускорением.
4.
За времятело
t
переместится из точки А в
точку В, пройдя небольшое
расстояние, s которое
стягивается малым углом
V
Рис.3.2
.
Изменение вектора скорости равно
.
Если t мало, то вектор V будет почти параллелен вектору
,
а
почти перпендикулярен им, то есть вектор
направлен к центру
окружности.
По определению ускорение a совпадает по направлению с
направлено к центру окружности.
, оно тоже
5.
Это ускорение и называют центростремительным ускорением.Обозначается как
и определяется по формуле:
an
2
r
.
6.
НЕРАВНОМЕРНОЕ ВРАЩАТЕЛЬНОЕДВИЖЕНИЕ
a
Рис.3.4
Если скорость частицы, вращающейся
по окружности, изменяется по
величине,
то
наряду
с
центростремительным
ускорением
будет иметь место и тангенциальное
ускорение
, которое возникает из-
за изменения величины вектора скорости. Тангенциальное
ускорение всегда направлено по касательной к
окружности, и, если скорость увеличивается, то его
направление совпадает с направлением движения
7.
ивсегда перпендикулярны друг другу, а их
направления непрерывно меняются по мере движения
тела по круговой траектории. Вектор полного ускорения
является суммой этих двух ускорений:
величина ускорения в любой момент времени равна
2
n
2
a a a
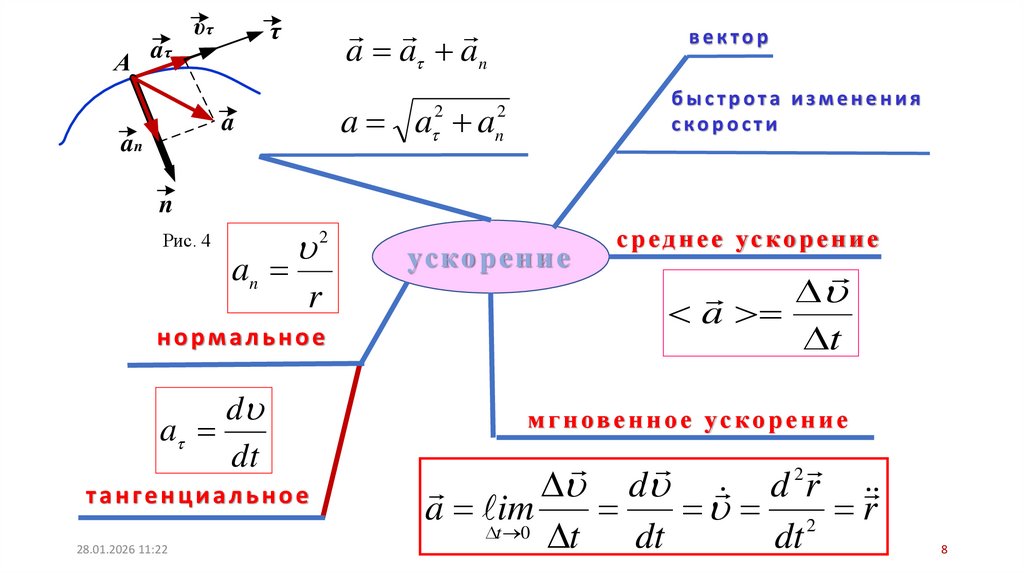
8.
υτА
a a an
τ
aτ
быстрота изменения
скорости
a a a
2
a
an
вектор
2
n
n
Рис. 4
an
2
с р е д н е е ус к о р е н и е
ус ко р е н и е
a
t
r
нормальное
d
a
dt
тангенциальное
28.01.2026 11:22
м г н ов е н н о е ус к о р е н и е
d d r
a im
2 r
t 0
t
dt
dt
2
8
9.
В РА Щ АТ Е Л Ь Н О Е Д В И Ж Е Н И ЕА B
С
Рис. 6
28.01.2026 11:22
9
10.
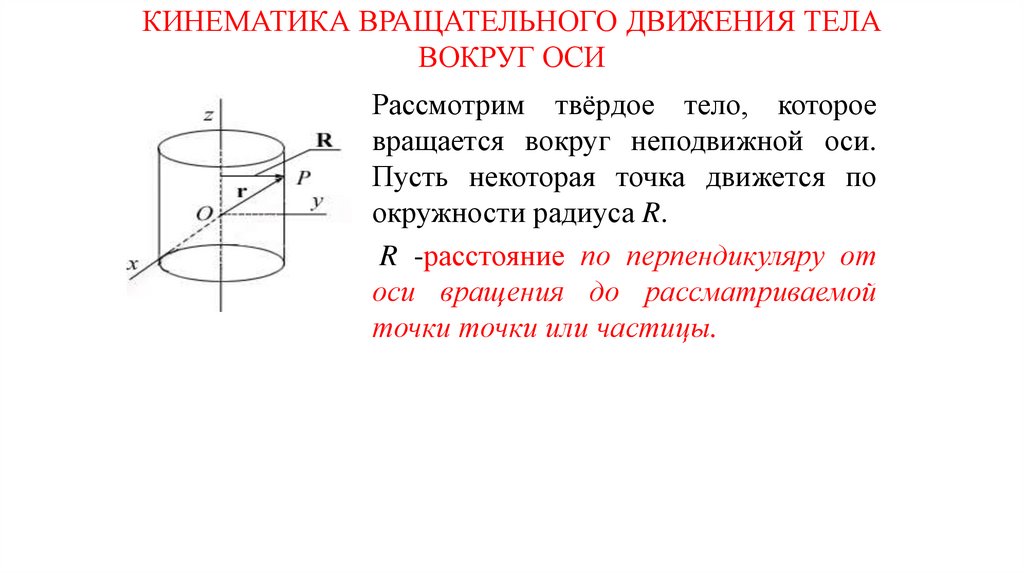
КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛАВОКРУГ ОСИ
Рассмотрим твёрдое тело, которое
вращается вокруг неподвижной оси.
Пусть некоторая точка движется по
окружности радиуса R.
R -расстояние по перпендикуляру от
оси вращения до рассматриваемой
точки точки или частицы.
11.
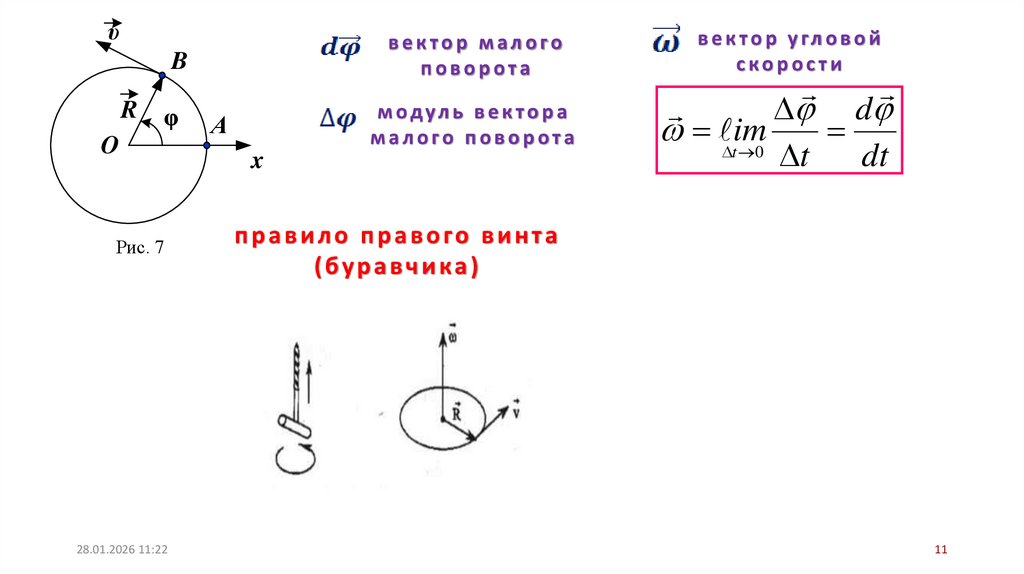
υB
R
φ
O
Рис. 7
28.01.2026 11:22
А
вектор малого
поворота
в е к т о р у гл о в о й
скорости
м одул ь в е к то р а
малого поворота
d
tim
0
t
dt
x
правило правого винта
(буравчика)
11
12.
3.3.1. УГЛОВАЯ СКОРОСТЬω
Пусть
некоторая
точка
движется
по
окружности
радиуса R. Её положение через
промежуток времени t зададим
углом d .
Элементарные углы поворота рассматривают как векторы. Модуль
вектора равен углу поворота, а его направление совпадает с
направлением поступательного движения острия винта, головка
которого вращается в направлении движения точки по окружности, то
есть подчиняется правилу правого винта.
13.
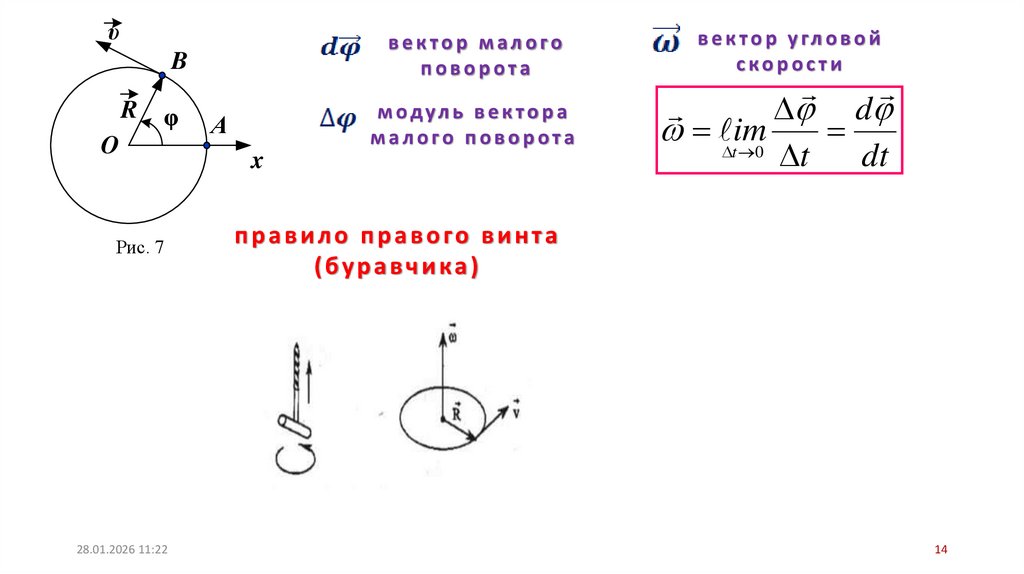
υB
R
φ
O
Рис. 7
28.01.2026 11:22
А
вектор малого
поворота
в е к т о р у гл о в о й
скорости
м одул ь в е к то р а
малого поворота
d
tim
0
t
dt
x
правило правого винта
(буравчика)
14
14.
SR
lim
R ,
t 0 t
t 0 t
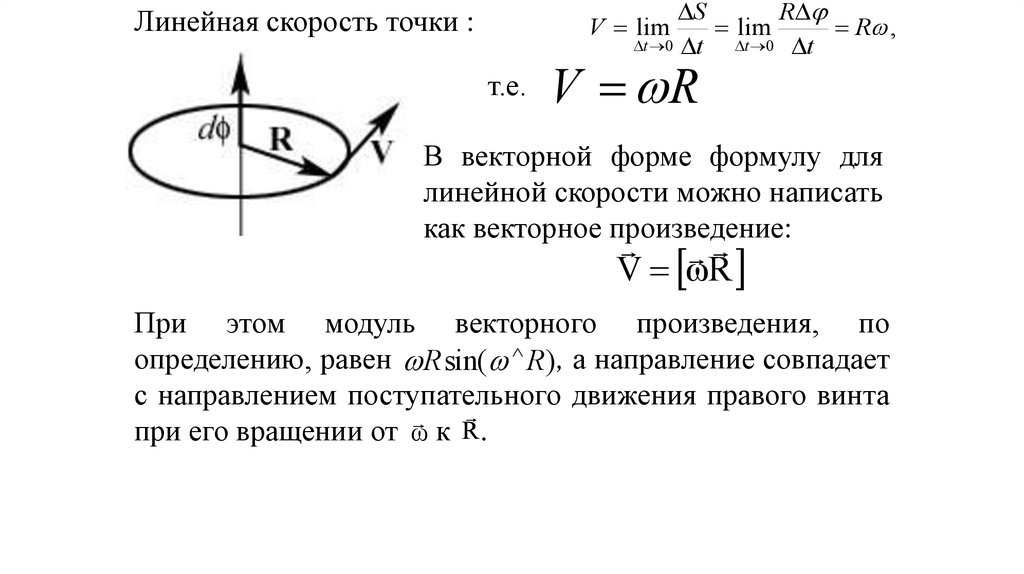
Линейная скорость точки :
V lim
т.е.
V R
В векторной форме формулу для
линейной скорости можно написать
как векторное произведение:
V ωR
При этом модуль векторного произведения, по
определению, равен R sin( R) , а направление совпадает
с направлением поступательного движения правого винта
R
при его вращении от ω к .
15.
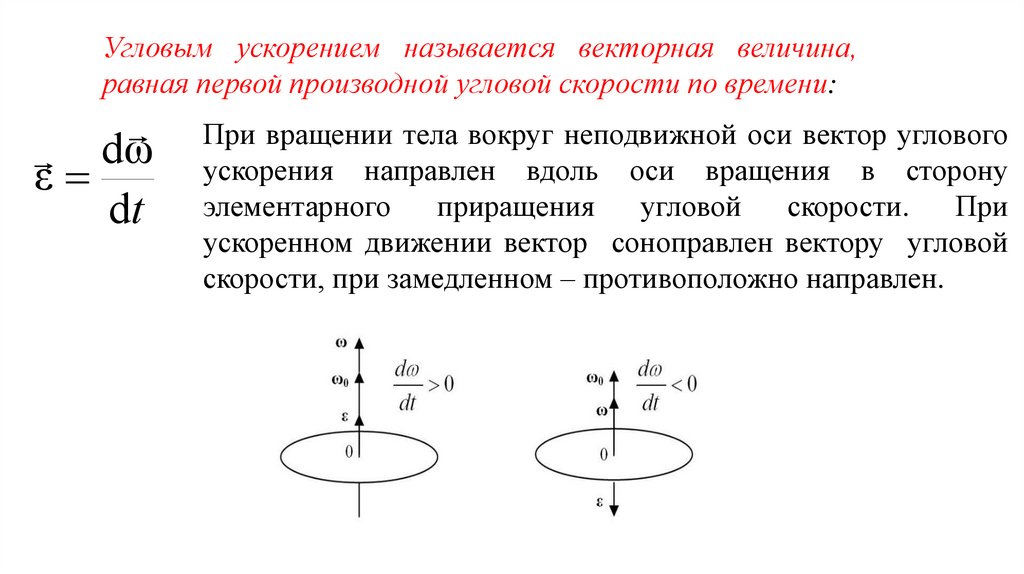
Угловым ускорением называется векторная величина,равная первой производной угловой скорости по времени:
dω
ε
dt
При вращении тела вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения в сторону
элементарного
приращения
угловой
скорости.
При
ускоренном движении вектор соноправлен вектору угловой
скорости, при замедленном – противоположно направлен.
16.
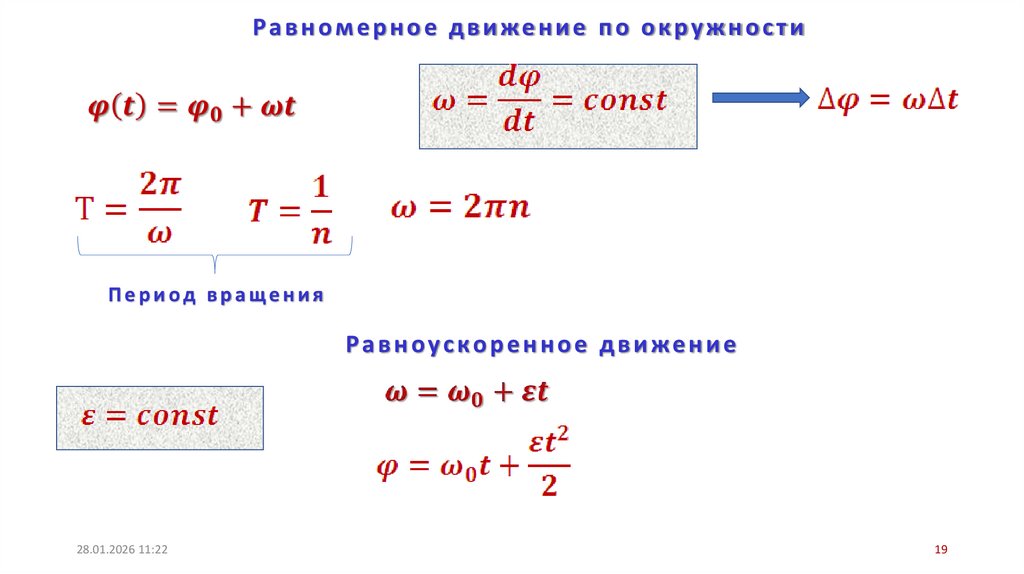
Если =const, то вращение равномерное и егоможно характеризовать периодом вращения Т –
временем, за которое точка совершает один полный
оборот, то есть поворачивается на угол 2 . Так как
промежутку Δt T времени соответствует Δ 2 ,
то 2 / T , откуда T 2 .
Число полных оборотов, совершаемых телом при
равномерном его движении по окружности, в единицу
времени называется частотой вращения:
1
n / 2 откуда
T
Рис.3.9.
2 n.
17.
Равномерное движение по окружностиПериод вращения
Равноускоренное движение
28.01.2026 11:22
19
18.
an28.01.2026 11:22
20
19.
28.01.2026 11:22Задача. Поезд движется по закруглению радиусом 100 м, причем зависимость
его координаты от времени дается уравнением x = Сt3, где С = 10 см/с3 –
постоянная величина. Найти полное ускорение поезда в тот момент, когда его
скорость 54 км/ч.
Решение
По теореме Пифагора:
21
20.
28.01.2026 11:22Скорость поезда найдем как первую производную координаты по времени:
Тогда
Время t можно найти из формулы (2):
Тогда (по формуле (3))
22
21.
Нормальное ускорение определяется по формуле:28.01.2026 11:22
23
22.
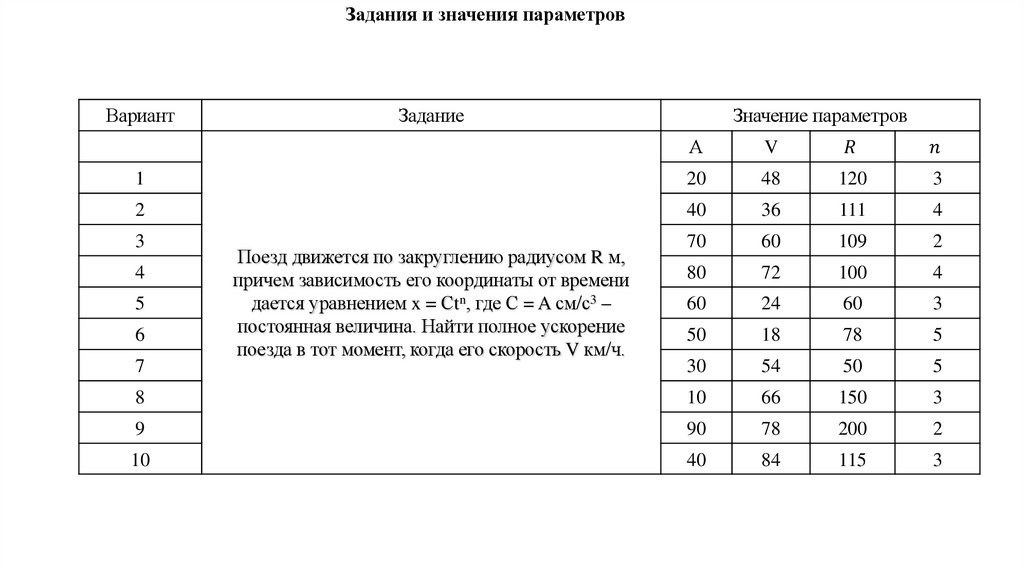
Задания и значения параметровВариант
Задание
Значение параметров
А
V
1
20
48
120
3
2
40
36
111
4
70
60
109
2
80
72
100
4
60
24
60
3
50
18
78
5
30
54
50
5
8
10
66
150
3
9
90
78
200
2
10
40
84
115
3
3
4
5
6
7
Поезд движется по закруглению радиусом R м,
причем зависимость его координаты от времени
дается уравнением x = Сtn, где С = A см/с3 –
постоянная величина. Найти полное ускорение
поезда в тот момент, когда его скорость V км/ч.










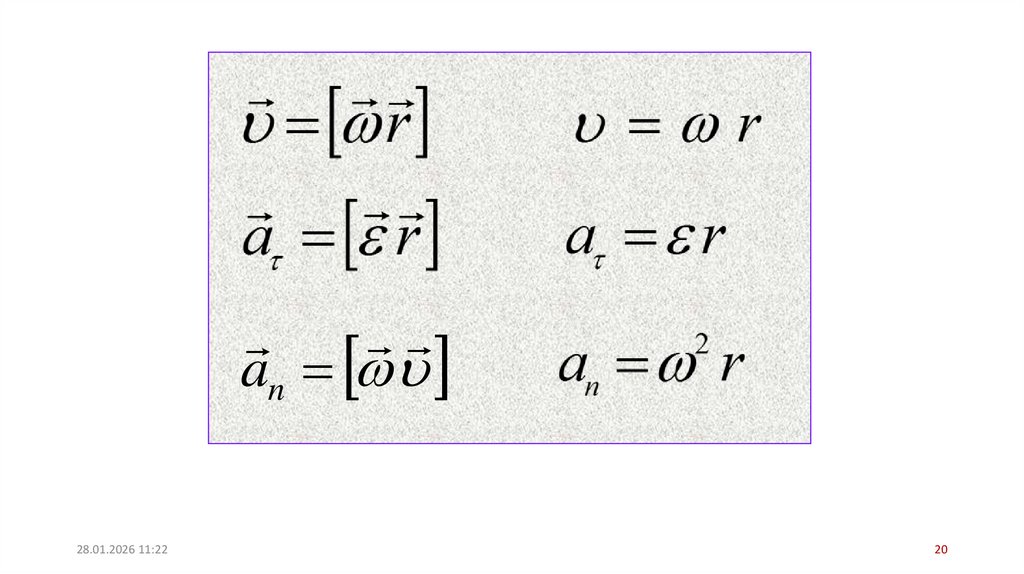



 Физика
Физика








