gradient_presentation

1.

Градиент функции
Функции трёх переменных, геометрический смысл и
применения
Краткий конспект с примерами вычисления и интерпретацией

2.

Определение: градиент как “компас” изменения
Пусть f: R³ → R — скалярная функция трёх переменных.
Смысл: это вектор из частных производных — он
объединяет “наклоны” по осям x, y, z в одну стрелку.
Как находить ∇f (практический алгоритм)
• 1) Записать f(x,y,z).
• 2) Найти ∂f/∂x, ∂f/∂y, ∂f/∂z (остальные
переменные считать константами).
• 3) Собрать вектор (∂f/∂x, ∂f/∂y, ∂f/∂z).
• 4) При необходимости подставить точку
(x₀,y₀,z₀).

3.

Частные производные: “замораживаем” остальные переменные
Частная производная измеряет, как меняется f при изменении одной переменной, когда остальные
фиксированы.
Сечения поверхности: наклоны касательных в направлениях осей дают ∂f/∂x и ∂f/∂y (аналогично для ∂f/∂z).

4.

Пример 1 (R³): вычисление ∇f и значение в точке
Шаг 1: частные производные
Шаг 2: подстановка точки
Интерпретация: в точке (1,2,0) функция
быстрее всего растёт в направлении вектора
(4,1,-1).

5.

Пример 2 (R³): экспонента и смешанные члены
Частные производные
В точке (0,1,2)
Компоненты показывают “чувствительность” g
к x, y, z в выбранной точке.

6.

Геометрическая интерпретация градиента
Ключевые факты (в любой размерности):
• ∇f указывает направление наискорейшего роста f.
• Норма ||∇f|| равна максимальной направленной
производной.
• ∇f перпендикулярен линиям/поверхностям уровня f =
const.
Если вы идёте по поверхности уровня (f = const), то
значение функции не меняется ⇒ направленная
производная вдоль касательной равна 0 ⇒ градиент
ортогонален этому уровню.

7.

Градиент как нормаль к поверхности уровня (пример: сфера)
z
∇F
В любой точке сферы ∇F направлен по радиусу наружу:
это нормаль к поверхности уровня.
x

8.

Направленная производная и максимум (связь через скалярное
произведение)
Если двигаться из точки a на малый шаг h в направлении единичного вектора u, то приращение функции на
первом порядке:
Почему максимум в направлении ∇f?
Dᵤf(a) = ∇f(a)·u.
По неравенству Коши–Буняковского:
∇f(a)·u ≤ ||∇f(a)||·||u|| = ||∇f(a)||.
Равенство достигается при u = ∇f/||∇f||.
Схема (векторное представление)
∇f
u
Чем меньше угол между u и ∇f, тем больше ∇f·u.

9.

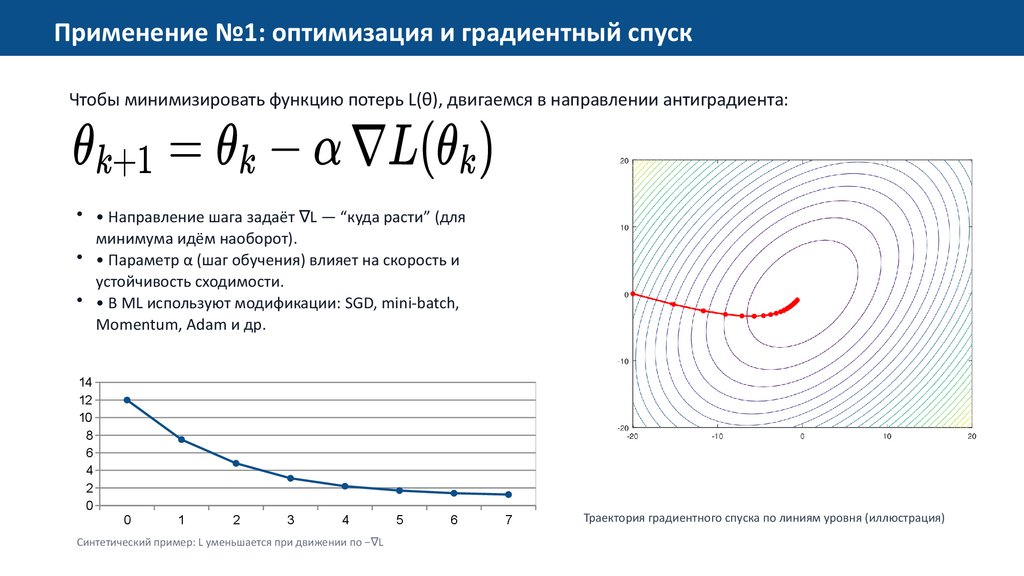
Применение №1: оптимизация и градиентный спуск
Чтобы минимизировать функцию потерь L(θ), двигаемся в направлении антиградиента:
• • Направление шага задаёт ∇L — “куда расти” (для
минимума идём наоборот).
• • Параметр α (шаг обучения) влияет на скорость и
устойчивость сходимости.
• • В ML используют модификации: SGD, mini-batch,
Momentum, Adam и др.
14
12
10
8
6
4
2
0
0
1
2
3
4
Синтетический пример: L уменьшается при движении по − ∇L
5
6
7
Траектория градиентного спуска по линиям уровня (иллюстрация)

10.

Применение №2: поля и потоки (физика, инженерия, данные)
1) Теплопроводность (Фурье):
3) Аналитика и ML:
Тепловой поток направлен в сторону убывания температуры
(против градиента).
• • Обучение моделей: градиент задаёт, как менять
параметры, чтобы уменьшать ошибку.
• • Чувствительность признаков: компоненты ∇f показывают,
на что модель реагирует сильнее локально.
• • Поиск экстремумов в задачах инженерного
проектирования и параметрической настройки.
2) Электростатика:
Электрическое поле — “ускорение” убывания потенциала.
4) Компьютерная графика/геометрия:
• • Нормали к неявным поверхностям: если поверхность
задана F(x,y,z)=0, то ∇F — нормаль.
• • Визуализация полей и “карт рельефа” (контуры,
изоповерхности).

11.

Мини‑памятка: как считать и как “читать” градиент
Вычисление
Интерпретация
• 1) Найдите ∂f/∂x, ∂f/∂y, ∂f/∂z.
• 2) Запишите ∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z).
• 3) Подставьте точку, если нужно получить численный
вектор.
• 4) Проверьте размерности/единицы измерения
(особенно в физике).
• • Направление ∇f — куда f растёт быстрее всего.
• • ||∇f|| — максимальная скорость роста при
движении единичным шагом.
• • Для уровня f=c: ∇f перпендикулярен поверхности
уровня.
• • Для минимума используйте −∇f (градиентный
спуск).
Контрольный вопрос для самопроверки
Если я двигаюсь в направлении касательной к поверхности уровня, почему ∇f·u = 0? (подсказка: на уровне f не меняется).

12.

Источники
• Яндекс Образование — “Частные производные и градиент”
• Skypro Wiki — “Как найти градиент функции: понятные способы и формулы”
• Wikipedia — “Thermal conduction” (Фурье: q = -k∇T)
• Physics LibreTexts — связь электрического поля и потенциала (E = -∇V)
• LibreTexts (Calculus III) — Directional Derivatives and the Gradient
• Hvidberrrg (Deep learning notes) — иллюстрации градиентного спуска