СВиCЧлек2022

1. Дисциплина МАТЕМАТИКА 1.1

Лектор:
доцент высшей
математики,
кандидат
педагогических наук
Тарбокова
Татьяна
Васильевна
1

2. Метод Гаусса (метод исключения неизвестных)

• Две системы называются
эквивалентными (равносильными),
если их решения совпадают.
• К эквивалентной системе можно
перейти с помощью элементарных
преобразований расширенной
матрицы этой системы.
2

3.

Исключение неизвестных обычно
осуществляют элементарными
преобразованиями строк
расширенной матрицы СЛУ.
В результате расширенная матрица
СЛУ приводится к ступенчатому
виду (к трапециевидной матрице),
который позволяет легко выделить
базисный минор основной матрицы
системы.
3

4.

• Неизвестные, коэффициенты
при которых вошли в базисный
минор называются базисными
неизвестными.
• Неизвестные, коэффициенты
при которых не вошли в
базисный минор, называются
свободными неизвестными.
4

5.

• Если n – число неизвестных
системы, r – её ранг, то
• r неизвестных системы –
базисные,
• k = n – r свободные.
5

6.

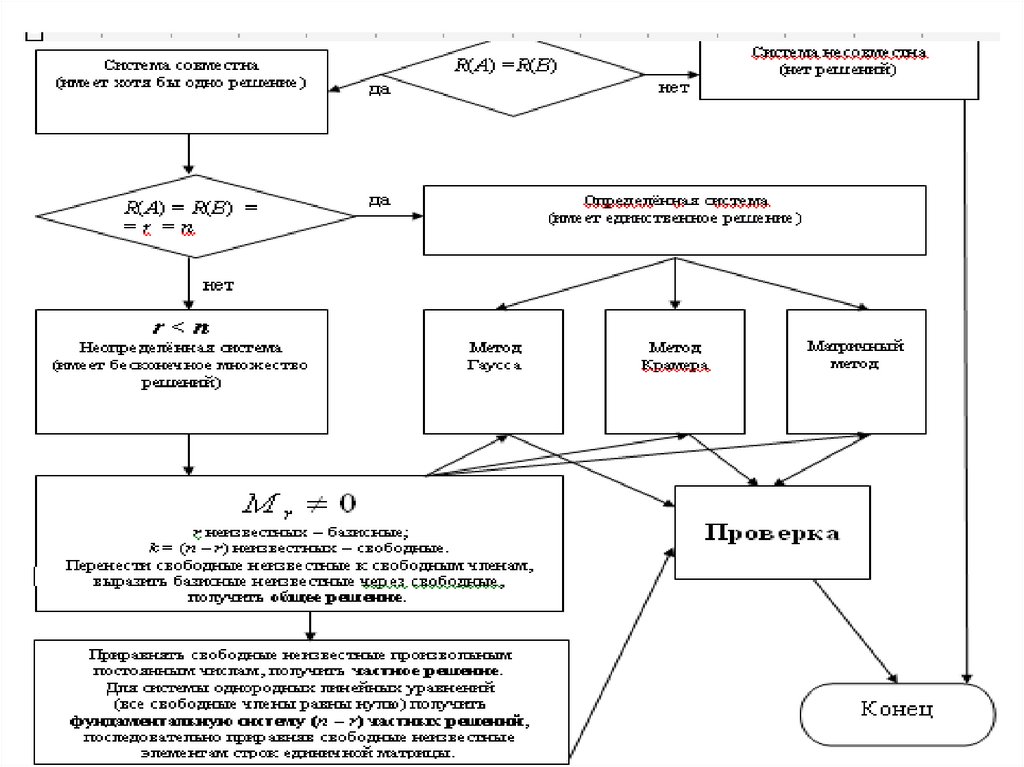
• Пусть ранг основной и расширенной
матриц СЛУ совпадает с числом
неизвестных СЛУ: r(A) = r(A*) = n,
• тогда свободных неизвестных нет. В
этом случае СЛУ имеет единственное
решение (определённая СЛУ).
• Если ранги основной и расширенной
матриц СЛУ равны, но меньше числа
неизвестных СЛУ: r(A) = r(A*) < n,
• то СЛУ неопределённая. В этом случае
находят общее решение СЛУ.

7.

• Решение СЛУ, в котором базисные
неизвестные выражены через
свободные неизвестные,
называется общим решением
СЛУ.
Решение, которое получается из
общего путём присваивания
свободным неизвестным числовых
значений, называется частным
решением СЛУ.
7

8.

• Общее решение системы линейных
уравнений можно получить, руководствуясь,
например, следующим планом:
• а) выбрать базисный минор (обычно это
минор, под главной диагональю которого –
все нули);
• б) перенести свободные неизвестные к
свободным членам, то есть в правые части
уравнений;
• в) обратным ходом метода Гаусса выразить
базисные неизвестные через свободные
неизвестные.
8

9. Найти общее решение СЛУ и какое-либо частное решение СЛУ

9

10. Запишем эквивалентную СЛУ:

10

11. § Системы однородных линейных уравнений (СОЛУ)

Уравнение называется линейным, если
неизвестные в нём содержатся только в
первой степени
и между собой не перемножаются,
т.е. если оно имеет вид a1 x1 a2 x2 ... an xn b
,
где ai,b – известные заданные числа,
x1 , x2 , ..., xn
- неизвестные уравнения.
ai называются коэффициентами уравнения,
b называется свободным членом.
Если b = 0, то уравнение называется
однородным.
Если b 0 , уравнение называется
11
неоднородным.

12.

12

13.

13

14.

14

15.

ТЕОРЕМА. Пусть r – ранг матрицы СЛОУ
n переменных.
Тогда существует n-r
линейно независимых решений
e1,e2,…en-r,,
и любое другое ее решение будет их
линейной комбинацией.
ОПР. Совокупность максимального числа
линейно-независимых
решений
СЛОУ
называется
фундаментальной системой
частных решений (ФСЧР).

16.

• Итак, фундаментальной
системой частных решений
(ФСЧР) системы n однородных
линейных уравнений (СОЛУ)
является система линейно
независимых частных решений,
число решений в которой равно
числу k = n – r свободных
неизвестных системы,
• где r - ранг основной матрицы
системы (следствие теорем 1 и 2).

17.

Фундаментальную систему частных
решений (ФСЧР СОЛУ) получают
обычно, последовательно
приравнивая свободные
неизвестные элементам строк
единичной матрицы порядка
k n r .
• Замечание. ФСЧР СОЛУ можно
получить также, приравнивая
свободные неизвестные элементам
строк произвольной квадратной
матрицы А порядка k = n – r, если
det A 0

18.

• Придавая свободным
переменным в общем
решении конкретные
значения,
• можно записать бесконечно
много решений системы.
• Их называют частные
решения
18

19.

• Линейная комбинация
частных решений
фундаментальной
системы является
общим решением
этой системы.
19

20.

20

21.

21

22.

22

23.

23

24. Собственные векторы матрицы

• Рассмотрим квадратную
матрицу A порядка n.
• Пусть X – матрица столбец
размерности n×1.
• Тогда произведение AX существует и
имеет размерность n×1.
• Ненулевая матрица-столбец
X называется собственным
вектором матрицы A,
• если существует число λ такое,
что AX = λX.
24

25.

• Число λ при этом называется
собственным значением
(собственным числом) матрицы A.
Говорят, что собственный вектор
X соответствует собственному
значению λ.
• Заметим, что вектор X ≠ O.
• Нулевой столбец удовлетворяет
условию AX = λX при любом значении λ,
но не считается собственным вектором
никакой матрицы.
25

26. Свойства собственных векторов и собственных значений

Свойства собственных векторов
и собственных значений
1. Собственный вектор матрицы соответствует
единственному собственному значению.
2. Каждому собственному значению матрицы
соответствует бесконечно много собственных
векторов.
3. Собственные векторы матрицы, соответствующие
различным собственным значениям, линейно
независимы.
4. Если X1 и X2 собственные векторы,
соответствующие одному собственному значению λ,
то их линейная комбинация αX1 + βX2 также является
собственным вектором, соответствующим этому же
собственному значению λ.
5. Квадратная матрица порядка n может иметь
не более n собственных значений.
26

27. Нахождение собственных значений матрицы

• Пусть задана квадратная
матрица A порядка n
• и X есть матрица-столбец. Преобразуем
равенство AX = λX следующим образом
• AX – λX = O, AX – λEX = O, (A – λE)X = O.
• Последнее равенство представляет собой
матричную запись системы n линейных
однородных уравнений с n
неизвестными x1, x2,…, xn.
• Система линейных однородных уравнений
имеет ненулевые (нетривиальные)
решения тогда и только тогда, когда
определитель этой системы равен нулю.
27

28.

Вычисляя определитель в правой части
последнего равенства (A – λE)X = O,
получим многочлен степени n относительно λ.
Этот многочлен называется
характеристическим многочленом матрицы A,
а уравнение det (A – λE) = 0 называется
характеристическим уравнением.
28

29.

• Теорема 1. Действительные корни
характеристического уравнения
матрицы, если они существуют, и
только они являются собственными
значениями этой матрицы.
• Теорема 2. Все собственные числа
матрицы совпадают с корнями её
характеристического многочлена.
29

30. Нахождение собственных векторов матрицы

Пусть задана квадратная матрица A порядка n .
Чтобы найти её собственные значения, необходимо
решить характеристическое уравнение det (A – λE) = 0.
Пусть λ0 есть собственное значение матрицы A.
Очевидно, собственные векторы, соответствующие
собственному значению λ0, являются ненулевыми
частными решениями системы линейных однородных
уравнений (A – λ0E)X = O.
Все решения системы линейных однородных
уравнений с n неизвестными образуют линейное
пространство размерности n – r, где r это ранг матрицы
этой системы. Базисом в этом линейном пространстве
является фундаментальная система решений (ФСЧР).
30

31.

• Таким образом, чтобы найти
собственные векторы матрицы следует:
• 1. Составить характеристическое
уравнение данной матрицы
• det (A – λE) = 0 и решить его;
• 2. Для каждого корня λ0
характеристического уравнения
(собственные значения) составить
систему линейных однородных
уравнений (A – λ0E)X = O
• и найти её ФСЧР.
31

32.

32

33.

33

34. Квадратичные формы (Данко П.Е., Попов А.Г.)

34

35. Приведение квадратичной формы к каноническому виду

35

36.

36

37.

37

38.

38

39.

39

40.

40

41.

41

42.

42

43.

43

44.

44

45. СПАСИБО ЗА ВНИМАНИЕ

45