Экстремум функции двух переменных

1.

Лектор: ОРЛИК ЛЮБОВЬ КОНСТАНТИНОВНА
Тема:
Экстремум функции двух переменных

2.

Пример 1.
z 1 x y
z M
P
2
2
- полусфера
y
x
В точке M - максимум, т.к. в
окрестности этой точки значения функции
меньше, чем
z в точке :
M
z ( P) z ( M ).

3.

z x y
2
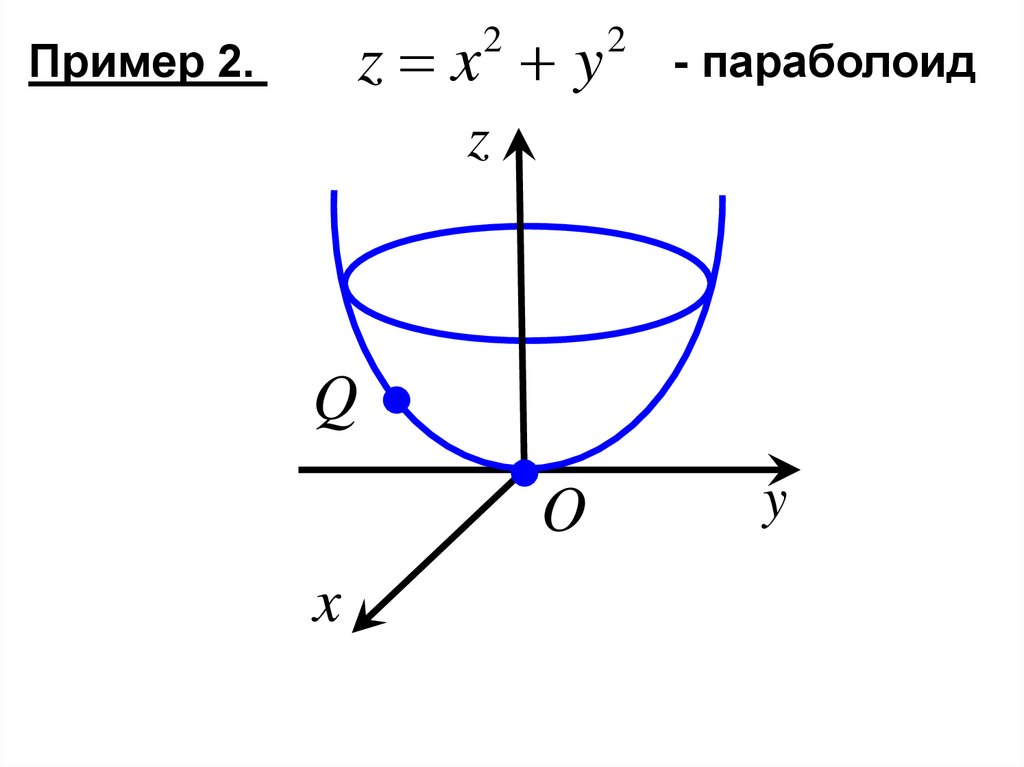
Пример 2.
2
- параболоид
z
Q
O
x
y

4.

В точке O(0,0) - минимум, т.к. в
окрестности этой точки значения функции
больше, чем
O
z в точке :
z (Q) z (O).

5.

Также, как и в случае функции одной
переменной для нахождения экстремума
находят критические точки.
Это точки, в которых z x и z y равны
нулю. Таким образом, обращение в нуль
в точке частных производных является
необходимым условием существования с
этой точке экстремума.

6.

Следовательно, точки экстремума
следует искать среди критических точек.
Однако существуют критические точки,
не являющиеся точками экстремума.
Поэтому рассмотрим достаточные
условия существования экстремума.

7.

Пусть
P0
- критическая точка.
Находим
A z xx ( P0 ), B z xy ( P0 ), C z yy ( P0 ).
Составим определитель
D
A B
B C
AC B .
2

8.

Возможны случаи:
A 0
min
A 0
max
I
D 0
II
D 0
Экстремума нет
D 0
Требуется
дополнительное
исследование
III

9.

Пример. Найти экстремумы функции
z x y 6 xy.
3
3
z x и z y :
2
2
z x 3x 6 y, z y 3 y 6 x.
1) Находим

10.

2) Составим систему уравнений
z x 0,
z
0.
y
3x 6 y 0,
2
3 y 6 x 0.
2
x 2 y 0,
1 2
y x .
2
2
y 2 x 0.
2

11.

Подставим
y
во второе уравнение
4
x
y 2 x 0 или
2x 0 :
4
4
3
x 8 x 0, x( x 8) 0;
2
x1 0;
x2 2.
Получили две критические точки
P1 (0,0)
и
P2 (2, 2).

12.

3) Находим
z xx , z xy , z yy :
z xx 3x 6 y 6 x,
2
x
z yy 3 y 6 x 6 y,
2
y
z xy 3x 6 y 6.
2
y

13.

4) Рассмотрим P1 (0,0) и находим
значения вторых производных в этой
точке:
A 6 x x 0 0,
B 6,
C 6 y y 0 0.
D
0
6
6
0
0 ( 6) 36 0
2
Следовательно экстремума нет.

14.

P2 (2,2) :
12, B 6, C 6 y y 2 12.
4) Рассмотрим
A 6 x x 2
D
12
6
6 12
12 12 6 6 144 36 108 0.
P2 (2, 2) функция имеет
экстремум, т.к. D 0.
В точке

15.

Чтобы выяснить, max или min в точке
P2 , смотрим на знак A или C.
A 0 в точке P2 (2,2) min.
z (2,2) 2 2 6 2 2 8 8 24 8.
3
3
Ответ: функция z x y 6 xy имеет
в точке P (2, 2) минимум,
3
2
zmin 8.
3

16.

Самостоятельная работа №2
1) Найти область определения функций
a) z xy ,
b) z
1
.
x y 1
2) Найти частные производные первого
и второго порядка
b) z x 3xy.
a) z x y ,
3
3) z x ln y, где y 5sin x.
dz
z
.
Найти
и
dx
x
3
4
2

17.

18. Условный экстремум: метод множителей Лагранжа

19.  

20.

21.  

22.  

23.  

24. Пример идея: сведём уравнение ,задающее функцию двух переменных ,к функции одной переменной с помощью уравнения связи (1)

25.  

26.  

27. cужение исходной функции -функцию исследуем на экстремум

cужение исходной функции функцию исследуем на
экстремум

28.  

29.  

30.  

31.  

32.  

33. МЕТОД МНОЖИТЕЛЕЙ ЛАГРАНЖА

34.  

35.  

36.  

37. исключить ,выразив из первых двух уравнений и приравняв результаты; ВЫРАЗИТЬ из первого уравнения X,из второго –Y и подставить в третье ур

исключить ,выразив из
первых двух уравнений и
приравняв результаты;
ВЫРАЗИТЬ из первого
уравнения X,из второго –Y и
подставить в третье уравнение
,которое будет зависеть только
от

38. Составить достаточные условия экстремума