Закон Ампера. Сила взаимодействия параллельных токов

1.

Кафедра физики
ЛЕКЦИЯ 3.
ПЛАН ЛЕКЦИИ
1. Закон Ампера. Сила взаимодействия параллельных токов.
2. Контур с током в магнитном поле.
3. Эффект Холла (самостоятельно).
4. Движение заряженных частиц в постоянном магнитном
поле (самостоятельно).
Общая физика. «Магнитостатика»

2.

Кафедра физики
ЗАКОН АМПЕРА
Электрические токи создают магнитное поле. В свою очередь
каждый носитель тока испытывает действие магнитной силы.
Действие этой силы передается проводнику, по которому заряды
движутся. В результате магнитное поле действует с определенной
силой на сам проводник с током. Определим эту силу.
Воспользуемся моделью единичных элементов тока.
Задача: определить силу dF, действующую на единичный элемент
B
тока dсо
другим элементом
l стороны магнитного поля , созданного
тока .
dl
Общая физика. «Магнитостатика»

3.

Кафедра физики
ЗАКОН АМПЕРА
v заряд q действует магнитная сила
Fм q v , B
На движущийся со скоростью
Если провод, по которому течет ток, поместить в магнитное поле,
эта сила действует на каждый из носителей тока.
Пусть n - число носителей тока, содержащихся в единице объема
проводника.
Тогда в элементе провода dl содержится n S dl носителей заряда
( S - площадь поперечного сечения проводника в том месте, где
располагается элемент тока).
На каждый из носителей тока будет действовать магнитная сила
.
, F
на все
носители
dl
e u , B в пределах
dF F nSdl ne u , B Sdl
u - средняя скорость упорядоченного движения носителей тока.
Общая физика. «Магнитостатика»

4.

Кафедра физики
ЗАКОН АМПЕРА
dF ne u , B Sdl
Внесем постоянные
ne под знак векторного произведения
величины
и, учтя, что ne u j, получим
dF j , B dV
dV Sdl - объем элемента провода.
Для тонкого проводника j dV Idl. Следовательно:
dF I dl , B
Общая физика. «Магнитостатика»
Выделенные формулы – это различные
формы записи закона Ампера. Силы,
действующие на токи в магнитном поле, силы Ампера.

5.

Кафедра физики
ЗАКОН АМПЕРА
dF j , B dV
dF I dl , B
j dV - объемные элементы тока.
Интегрирование выражений по объемным
или линейным элементам тока даст
магнитную силу, действующую на объем проводника или его
линейный участок.
Направление силы Ампера:
векторы dl , B и dF образуют правовинтовую ортогональную
тройку векторов.
dF IB dl sin
- угол между векторами dl и B .
Модуль силы Ампера:
Общая физика. «Магнитостатика»

6.

Кафедра физики
ЗАКОН АМПЕРА
Сила взаимодействия двух параллельных токов
Рассмотрим два бесконечных прямолинейных проводника с токами
и
, расстояние
R
I 1 I 2 между которыми равно .
Пусть токи в проводниках текут в одном направлении, «к нам».
I1
R
I2
Каждый из проводников создает магнитное
поле, которое действует в соответствии с
законом Ампера на другой проводник с
током.
Определим
силу, с которой действует магнитное поле тока I 1на
элемент dl второго проводника с током I 2.
Общая физика. «Магнитостатика»

7.

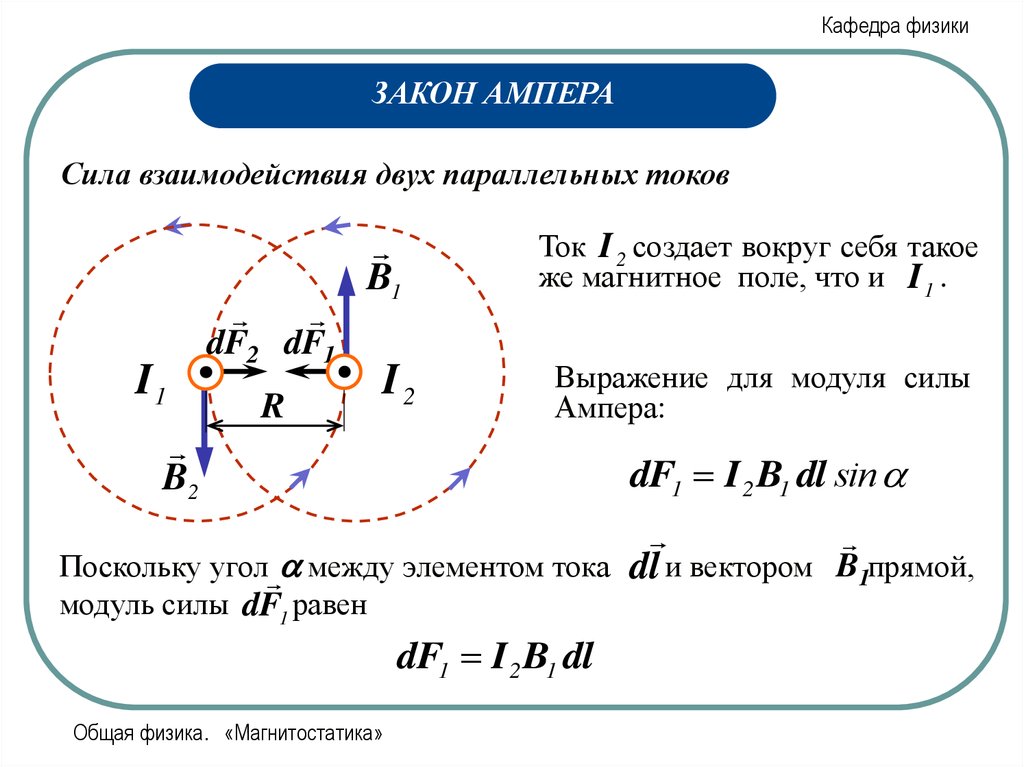
Кафедра физики
ЗАКОН АМПЕРА
Сила взаимодействия двух параллельных токов
Ток I 1 создает вокруг себя
магнитное
поле,
линии
магнитной индукции которого B1
концентрические окружности.
I1
dF1
R
I2
Направление линий магнитной
индукции .
определяется
правилом
правого
винта,
модуль вектора B1 равен
0 I 1
B1
2 R
Направление силы dF1 , с которой поле B1 действует на элемент dl .
тока I 2 , определяется из закона Ампера dF I dl , B .
Общая физика. «Магнитостатика»

8.

Кафедра физики
ЗАКОН АМПЕРА
Сила взаимодействия двух параллельных токов
I1
dF2 dF1
R
B1
I2
Ток I 2 создает вокруг себя такое
же магнитное поле, что и I 1 .
Выражение для модуля силы
Ампера:
B2
dF1 I 2 B1 dl sin
Поскольку угол между элементом тока
модуль силы dF1 равен
dF1 I 2 B1 dl
Общая физика. «Магнитостатика»
dl и вектором B1прямой,

9.

Кафедра физики
ЗАКОН АМПЕРА
Сила взаимодействия двух параллельных токов
I1
B2
dF2 dF1
R
B1
I2
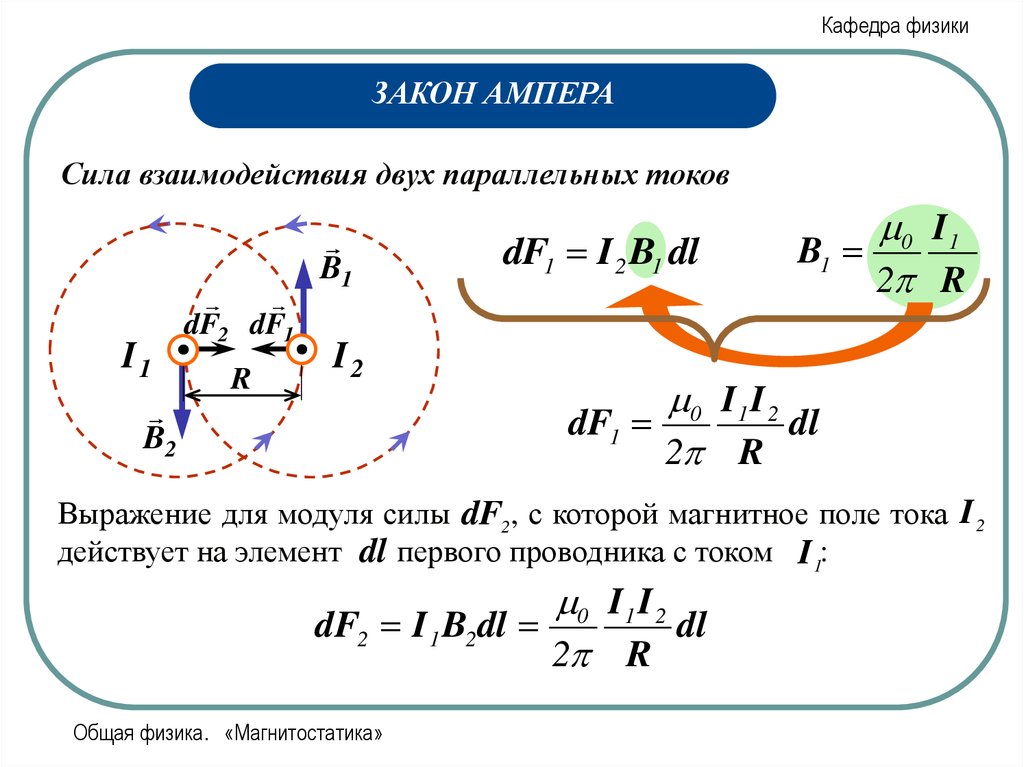
dF1 I 2 B1 dl
0 I 1
B1
2 R
0 I1 I 2
dF1
dl
2 R
Выражение для модуля силы dF2, с которой магнитное поле тока I.2
действует на элемент dl. первого проводника с током I1:
0 I1 I 2
dF2 I 1 B2dl
dl
2 R
Общая физика. «Магнитостатика»

10.

Кафедра физики
ЗАКОН АМПЕРА
Сила взаимодействия двух параллельных токов
I1
B2
dF2 dF1
R
B1
I2
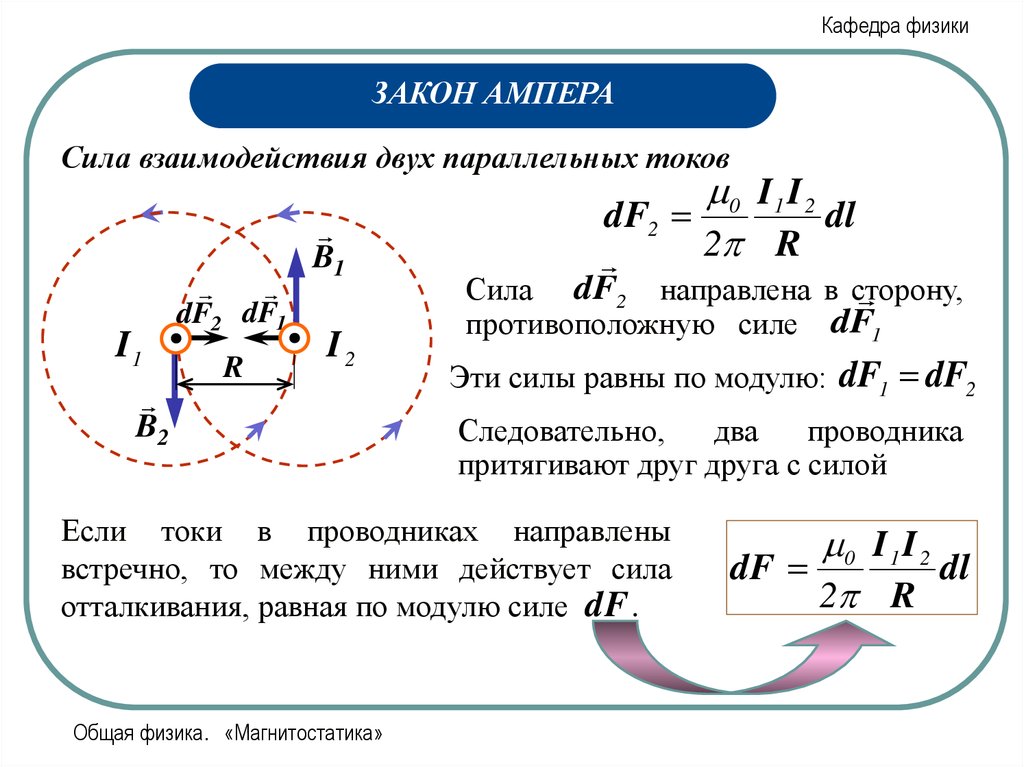
0 I 1 I 2
dF2
dl
2 R
Сила dF2 направлена в сторону,
противоположную силе dF1
Эти силы равны по модулю:
Следовательно,
два
проводника
притягивают друг друга с силой
Если токи в проводниках направлены
встречно, то между ними действует сила
отталкивания, равная по модулю силе dF .
Общая физика. «Магнитостатика»
dF1 dF2
0 I 1 I 2
dF
dl
2 R

11.

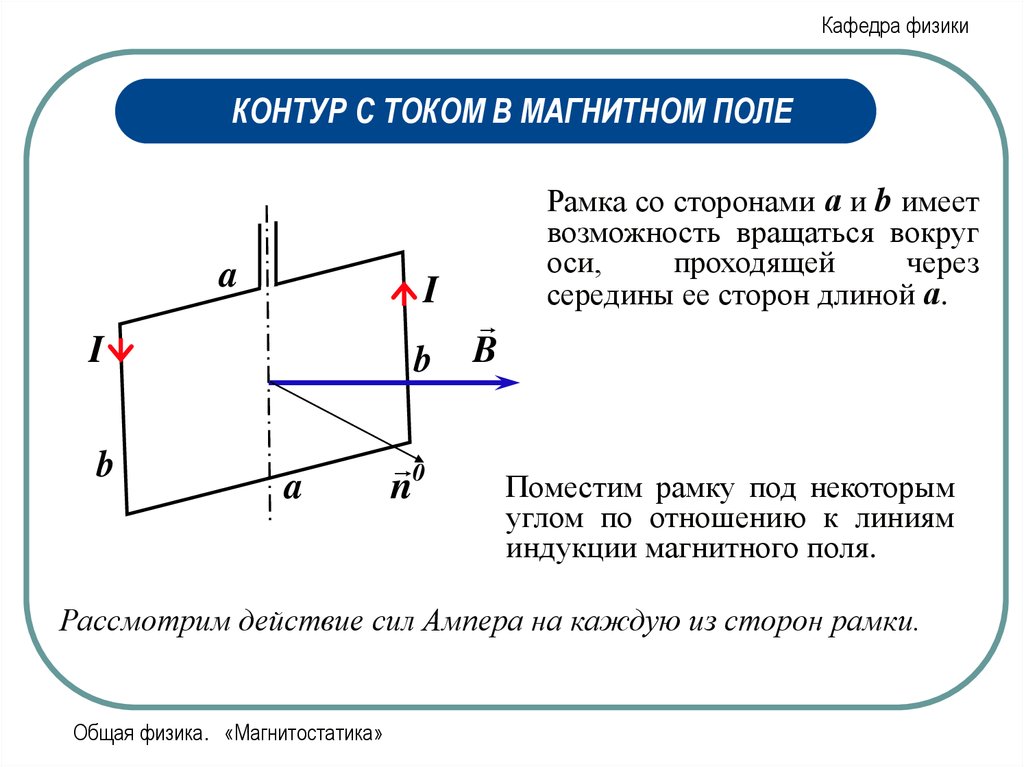
Кафедра физики
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
a
I
I
b
b
0
n
a
B
Рамка со сторонами а и b имеет
возможность вращаться вокруг
оси,
проходящей
через
середины ее сторон длиной а.
Поместим рамку под некоторым
углом по отношению к линиям
индукции магнитного поля.
Рассмотрим действие сил Ампера на каждую из сторон рамки.
Общая физика. «Магнитостатика»

12.

Кафедра физики
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
a
F
I
b
F
a
I
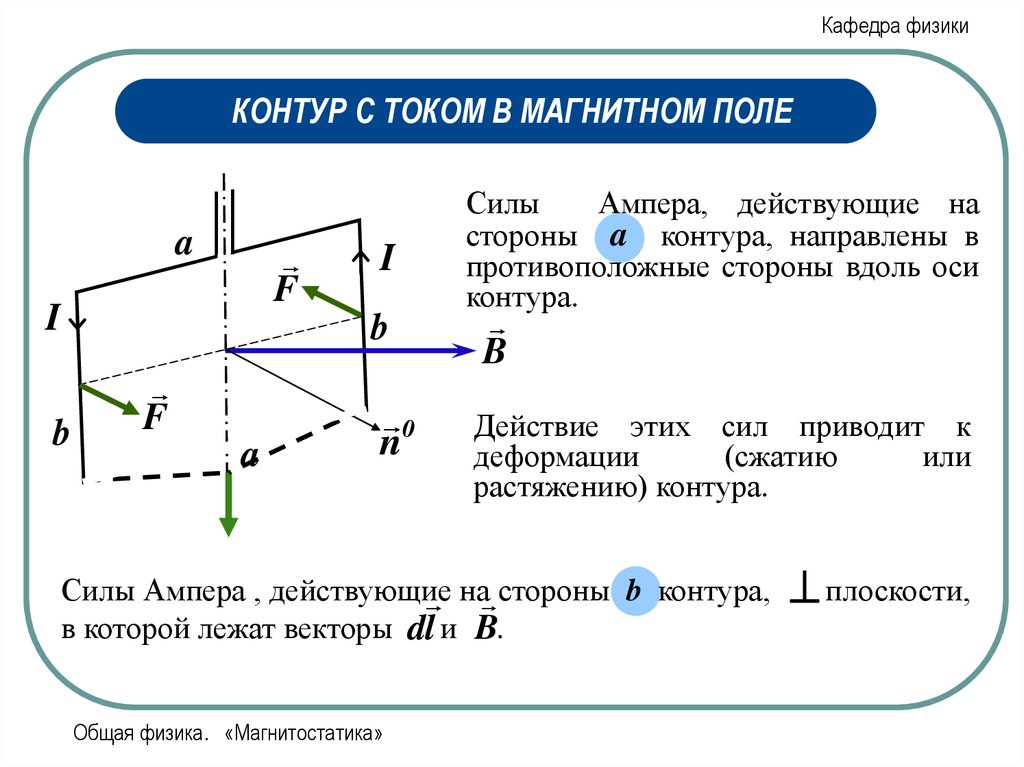
Силы
Ампера, действующие на
стороны a контура, направлены в
противоположные стороны вдоль оси
контура.
b
B
0
n
Действие этих сил приводит к
деформации
(сжатию
или
растяжению) контура.
Силы Ампера , действующие
на стороны b контура,
в которой лежат векторы dl и B.
Общая физика. «Магнитостатика»
плоскости,

13.

Кафедра физики
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
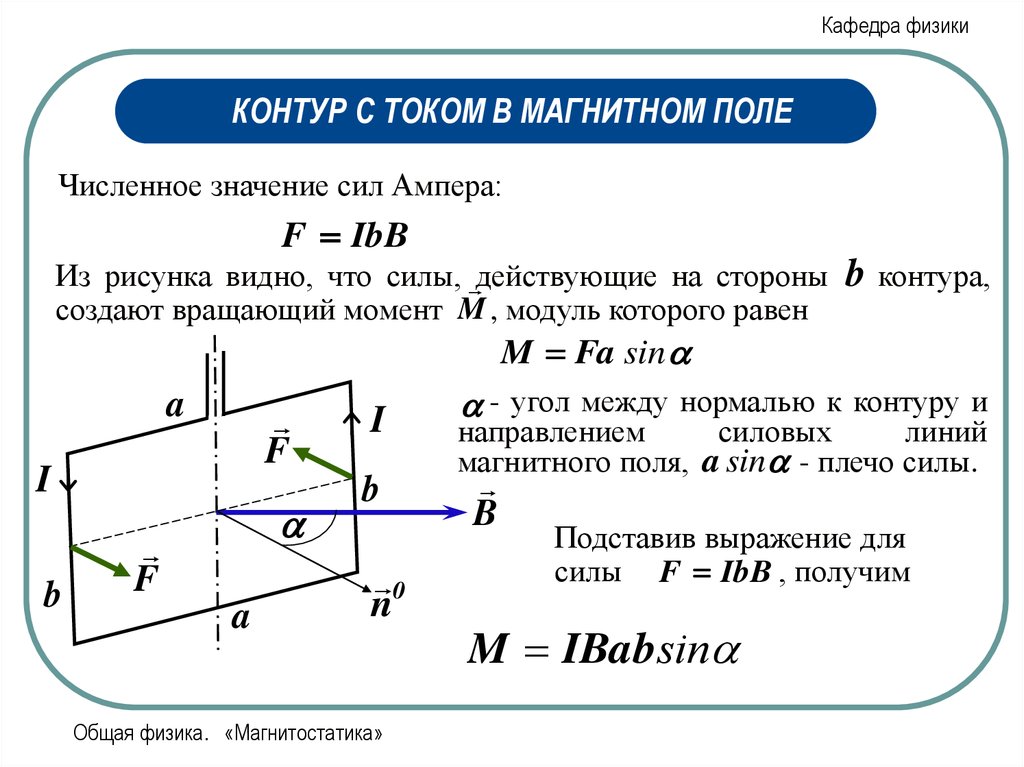
Численное значение сил Ампера:
F IbB
Из рисунка видно, что силы, действующие на стороны .b контура,
создают вращающий момент M , модуль которого равен
M Fa sin
a
F
I
b
F
a
I
b
0
n
Общая физика. «Магнитостатика»
- угол между нормалью к контуру и
направлением
силовых
линий
магнитного поля, a sin - плечо силы.
B
Подставив выражение для
силы F IbB , получим
M IBabsin

14.

Кафедра физики
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
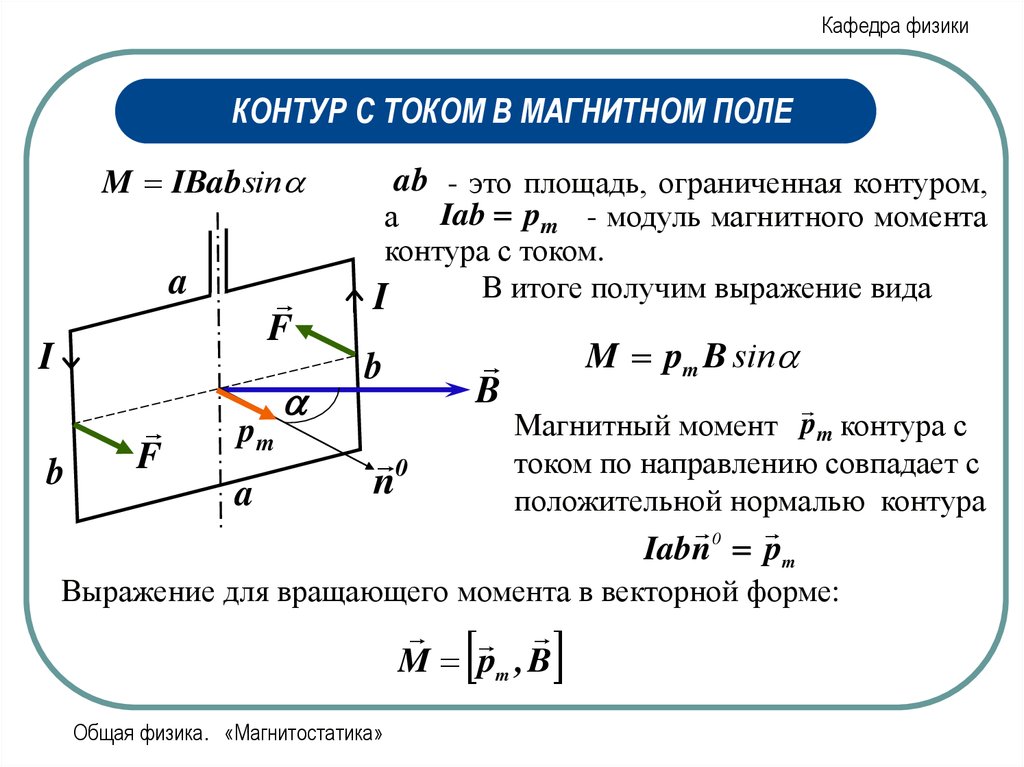
M IBabsin
a
F
I
b
F
pm
a
ab - это площадь, ограниченная контуром,
а Iab pm - модуль магнитного момента
контура с током.
В итоге получим выражение вида
I
B
b
0
n
M pm B sin
Магнитный момент pm контура с
током по направлению совпадает с
положительной нормалью контура
0
Iabn pm
Выражение для вращающего момента в векторной форме:
M pm , B
Общая физика. «Магнитостатика»

15.

Кафедра физики
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
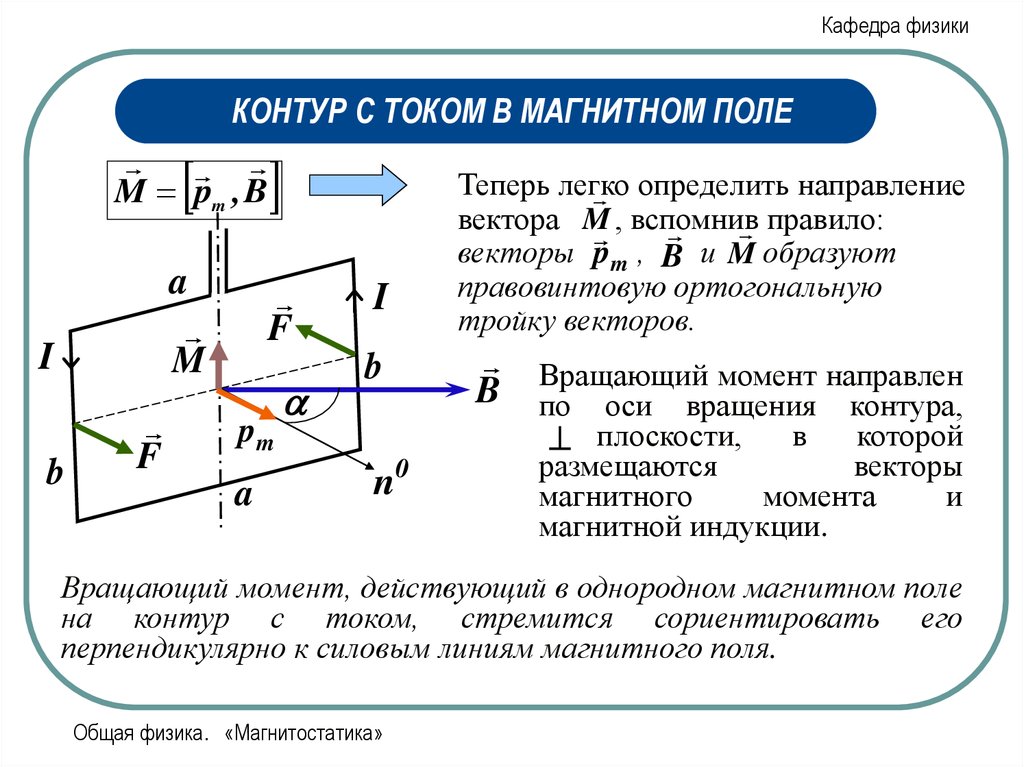
Теперь легко
M pm , B
определить направление
вектора M
правило:
, вспомнив
векторы pm , B и M образуют
I
b
F
a
M
F
pm
a
I
b
n0
правовинтовую ортогональную
тройку векторов.
Вращающий момент направлен
B по оси вращения контура,
. плоскости,
в
которой
размещаются
векторы
магнитного
момента
и
магнитной индукции.
Вращающий момент, действующий в однородном магнитном поле
на контур с током, стремится сориентировать его
перпендикулярно к силовым линиям магнитного поля.
Общая физика. «Магнитостатика»

16.

Кафедра физики
КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ
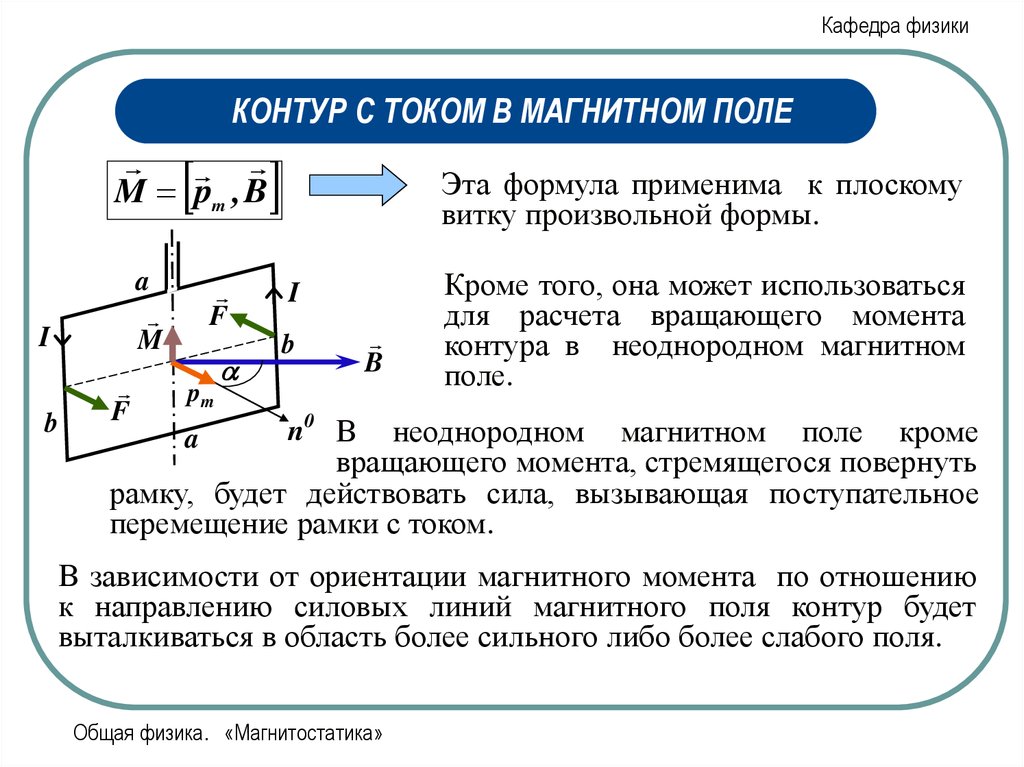
Эта формула применима к плоскому
M pm , B
a
M
I
b
F
F
pm
витку произвольной формы.
I
b
B
Кроме того, она может использоваться
для расчета вращающего момента
контура в неоднородном магнитном
поле.
неоднородном магнитном поле кроме
вращающего момента, стремящегося повернуть
рамку, будет действовать сила, вызывающая поступательное
перемещение рамки с током.
a
n0 В
В зависимости от ориентации магнитного момента по отношению
к направлению силовых линий магнитного поля контур будет
выталкиваться в область более сильного либо более слабого поля.
Общая физика. «Магнитостатика»

17.

Кафедра физики
ЭФФЕКТ ХОЛЛА
ИЗУЧИТЬ САМОСТОЯТЕЛЬНО.
Общая физика. «Магнитостатика»

18.

Кафедра физики
ЭФФЕКТ ХОЛЛА
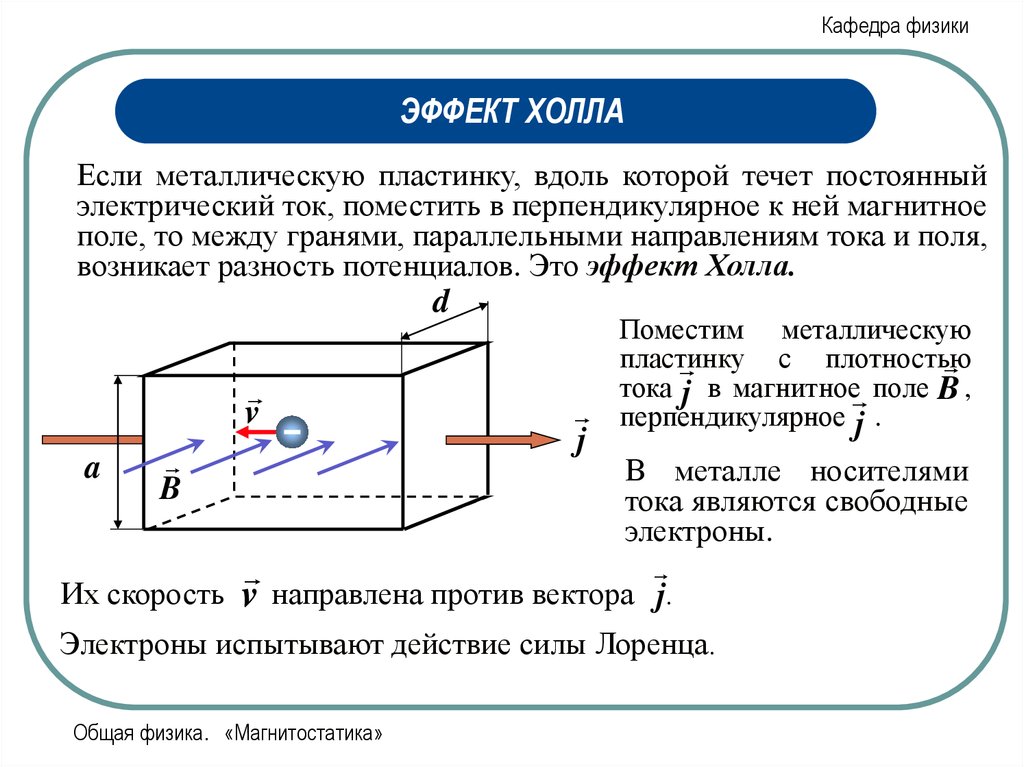
Если металлическую пластинку, вдоль которой течет постоянный
электрический ток, поместить в перпендикулярное к ней магнитное
поле, то между гранями, параллельными направлениям тока и поля,
возникает разность потенциалов. Это эффект Холла.
d
v
a
B
j
Поместим металлическую
пластинку
с плотностью
тока j в магнитное поле B ,
перпендикулярное j .
В металле носителями
тока являются свободные
электроны.
Их скорость v направлена против вектора j.
Электроны испытывают действие силы Лоренца.
Общая физика. «Магнитостатика»

19.

Кафедра физики
ЭФФЕКТ ХОЛЛА
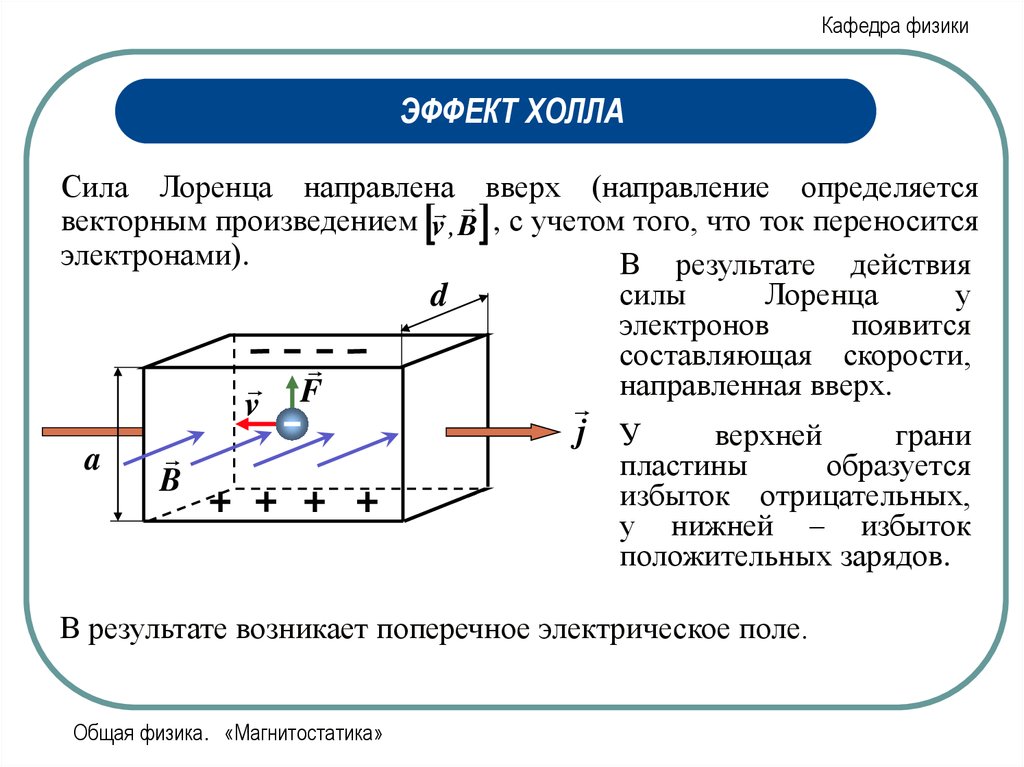
Сила Лоренца направлена вверх (направление определяется
векторным произведением v , B , с учетом того, что ток переносится
электронами).
В результате действия
силы
Лоренца
у
d
электронов
появится
составляющая скорости,
F
направленная вверх.
v
a
B
j У
верхней
грани
пластины
образуется
избыток отрицательных,
у нижней – избыток
положительных зарядов.
В результате возникает поперечное электрическое поле.
Общая физика. «Магнитостатика»

20.

Кафедра физики
ЭФФЕКТ ХОЛЛА
d
v
a
F
B
j
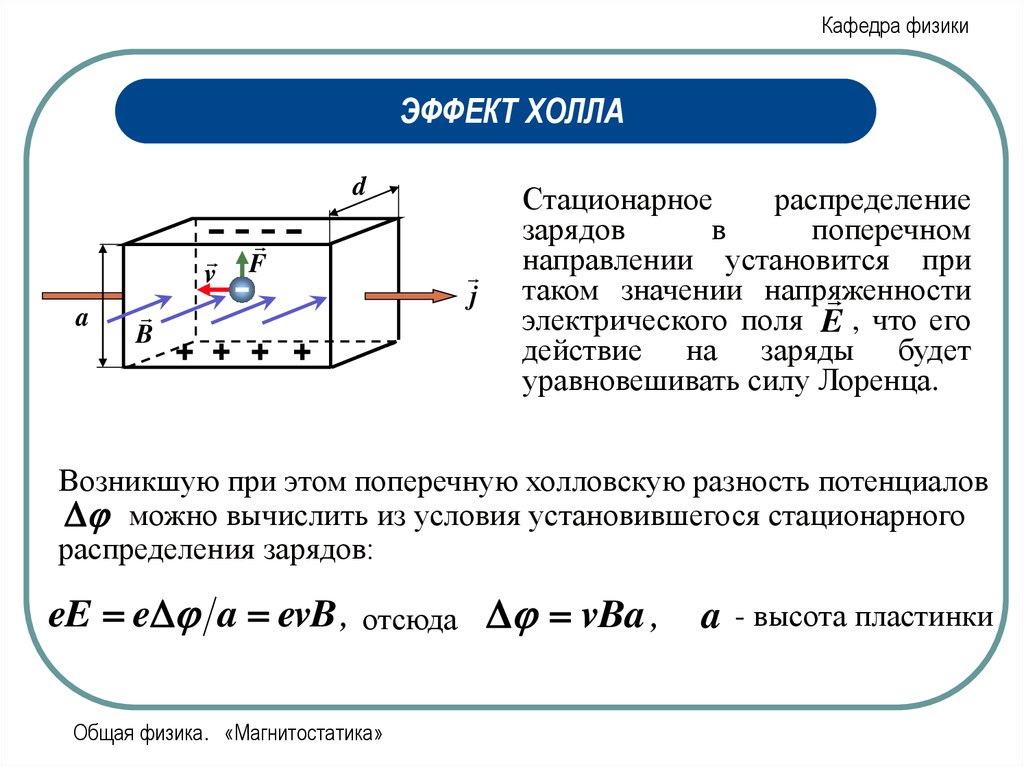
Стационарное
распределение
зарядов
в
поперечном
направлении установится при
таком значении напряженности
электрического поля E , что его
действие на заряды будет
уравновешивать силу Лоренца.
Возникшую при этом поперечную холловскую разность потенциалов
. можно вычислить из условия установившегося стационарного
распределения зарядов:
eE e a evB , отсюда vBa ,
Общая физика. «Магнитостатика»
a
- высота пластинки

21.

Кафедра физики
ЭФФЕКТ ХОЛЛА
d
v
a
F
B
vBa
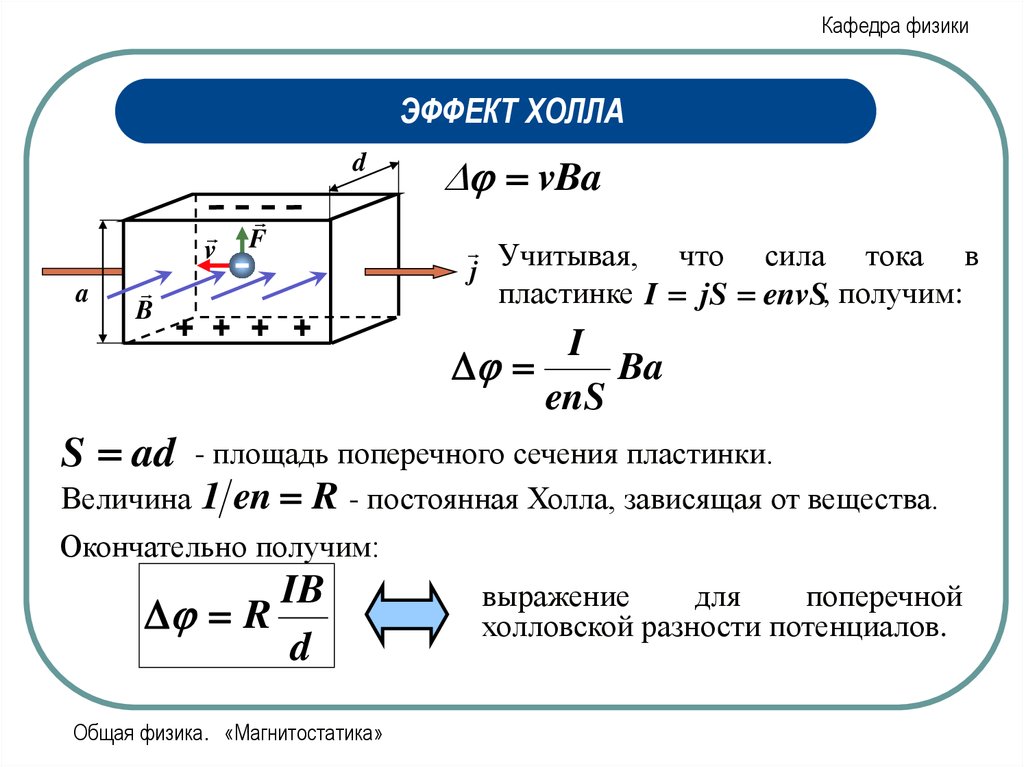
Учитывая,
j
что сила тока в
пластинке I jS envS, получим:
I
1 IBa 1 IB
Ba
enS
en ad
en d
S ad
- площадь поперечного сечения пластинки.
Величина 1 en R - постоянная Холла, зависящая от вещества.
Окончательно получим:
IB
R
d
Общая физика. «Магнитостатика»
выражение
для
поперечной
холловской разности потенциалов.

22.

Кафедра физики
ЭФФЕКТ ХОЛЛА
d
v
a
F
B
j
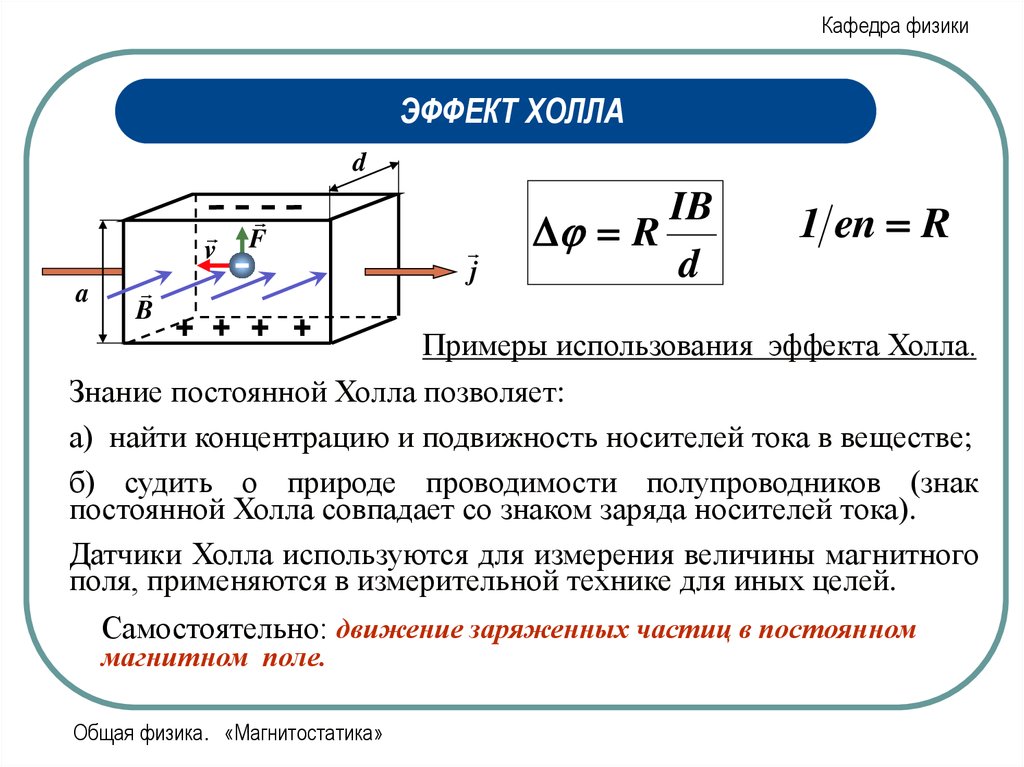
IB
R
d
1 en R
Примеры использования эффекта Холла.
Знание постоянной Холла позволяет:
а) найти концентрацию и подвижность носителей тока в веществе;
б) судить о природе проводимости полупроводников (знак
постоянной Холла совпадает со знаком заряда носителей тока).
Датчики Холла используются для измерения величины магнитного
поля, применяются в измерительной технике для иных целей.
Самостоятельно: движение заряженных частиц в постоянном
магнитном поле.
Общая физика. «Магнитостатика»