Похожие презентации:
Замена переменной в двойном интеграле
1.
Пусть функция f(x,y) непрерывна в некоторойзамкнутой ограниченной области D, и существует
f ( x, y)dxdy
D
Предположим, что возможен переход к новым
переменным:
( x, y ) (u, v)
2.
x x (u , v )y y (u , v )
u u ( x, y )
v v ( x, y )
3.
Пусть преобразование x=x(u,v), y=y(u,v)переводит замкнутую ограниченную
область
D
в
замкнутую
ограниченную область D* и является
взаимно однозначным.
Если функции x(u,v), y(u,v) имеют в D*
непрерывные частные производные,
и выражение
4.
x( xy)
u
y
(uv )
u
x
v 0
y
v
то имеет место
5.
f ( x, y)dxdyD
D
( xy)
f x(u, v), y (u, v)
dudv
(uv)
6.
x( xy)
u
y
(uv )
u
x
v
y
v
7.
1Вычислить двойной интеграл
sin( x y) dxdy
D
где область D ограничена линиями
x y,
x y
2
,
y 0
8.
Введем новые переменные:x y u
x y v
u v
x
2
u v
y
2
9.
Тогда прямая x y2
u
переходит в прямую
2
Прямая
x y
переходит в прямую
v 0
Прямая
y 0
переходит в прямую
v u
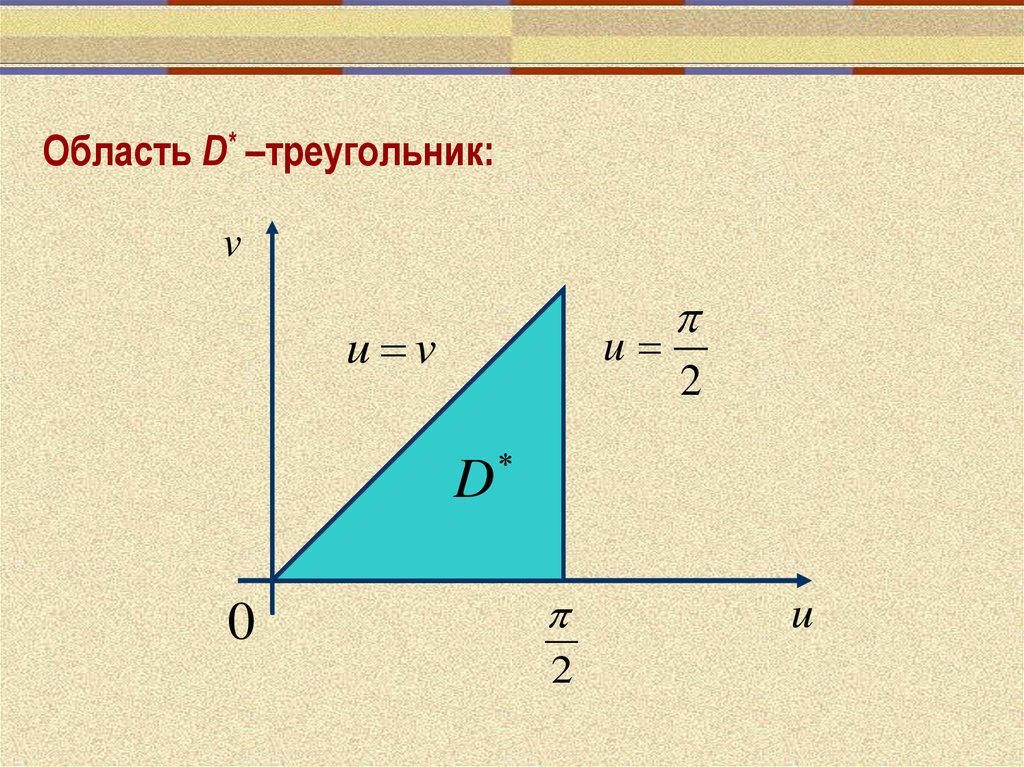
10.
Область D* –треугольник:v
u
u v
D
0
2
2
u
11.
Найдем якобиан:x 1
u 2
x 1
v 2
1
( xy)
2
1
(uv )
2
y 1
u 2
1
2 1
1
2
2
( xy) 1
(uv) 2
y
1
v
2
12.
11
D sin( x y) dxdy 2 sin ududv 2
D
1
2
2
1
0 du sin u v 0 2
u
2
u
du sin udv
0
0
2
du sin u u
0
2
1
1
1
1
2
2
u cos u 0 cos udu sin u 0
2
2 0
2
2
0
13.
2Вычислить двойной интеграл
e
x2 y2
dxdy
D
где область D ограничена осью х и
верхней полуокружностью
x y 1
2
2
14.
Область D –полуокружность:y
1
D
1
0
1
x
15.
Введем новые переменные:x cos
y sin
0
Прямая
y 0
переходит в прямую
Полуокружность
переходит в прямую
x y 1
2
2
1
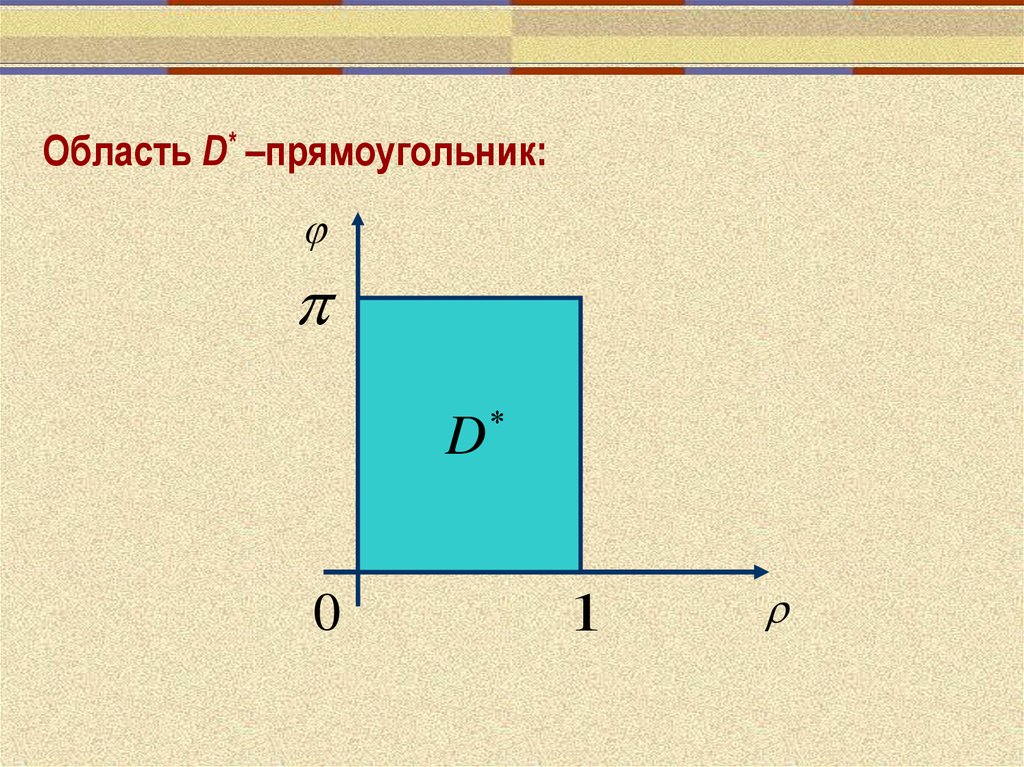
16.
Область D* –прямоугольник:D
0
1
17.
Найдем якобиан:x
cos
x
sin
y
cos
y
sin
(xy) cos sin
2
2
cos sin
( ) sin cos
(xy)
( )
18.
ex2 y2
1
0
0
dxdy e d d d e d
2
D
D
1
2
1
1 2
1
d e d e (e 1)
2 2
2
0 0
2
0










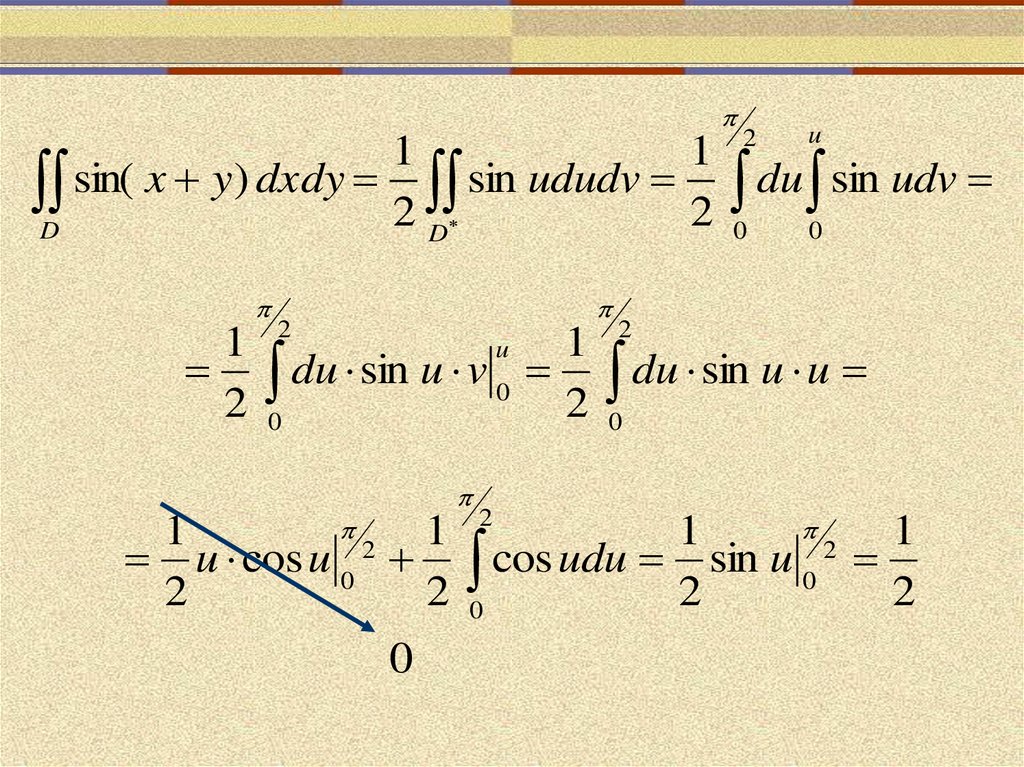





 Математика
Математика








