Классическая электродинамика вакуума

1. Классическая электродинамика вакуума -2

1 H
rot E
c t
div H 0
1 E
rot H
c t
div E 0

2. Плоские волны. Векторная структура поля излучения

Для плоских волн напряженности зависят только от одной
декартовой координаты и времени. Свойство поперечности
плоских волн
Ez
0 E z E z (t ),
z
1 H
dEz
rot
E
c (rot H ) z 0,
H z
c
t
dt
div H 0
0 H z H z (t ).
z
1 E
dH z
div E 0
rot H
c t
dt
c (rot E) z 0.
Опуская не интересующие нас однородные статические поля
Ez H z 0
(E,e z ) (H,e z ) 0
(E, m) (H, m) 0.
m – (единичный) вектор вдоль направления распространения
волны. При этом автоматически выполняются уравнения
Максвелла
div H 0
div E 0

3. Плоские волны. Векторная структура поля излучения*

ex
ey
rot E 0
0
Ex
Ey
ex
ey
rot H 0
0
Hx
Hy
ez
E y
E x
ex
e y [e z E],
z
z
z
z
0
ez
[e z H ].
z z
0
1 H
[e z E]
,
z
c t
1 H
rot E
c t
1 E
rot H
c t
1 E
[e z H ]
.
z
c t

4. Плоские волны. Векторная структура поля излучения*

Из двух встречных волн (см. решение Даламбера) рассмотрим
одну, бегущую в положительном направлении оси z. Для нее
E E( ), H H( ), z ct.
1 H
1 E
[e z E]
,
[e z H]
z
c t
z
c t
d
d
[e z E] H 0,
[e z H] E 0.
d
d
Опускаем несущественную постоянную составляющую
(статическое однородное поле)
H [e z E], E [e z H].
H [m E], E [m H].

5. Плоские волны. Векторная структура поля излучения*

H [m E], E [m H].
В (однонаправленной) плоской волне векторы E, H и m
образуют ортогональную тройку.
Инвариант E2 H2 0 - модули напряженностей
электрического и магнитного полей совпадают.
Инвариант (E, H ) 0 - векторы Е и Н ортогональны.
Задание. Вычислить инварианты стоячей плоской
волны с линейной поляризацией.

6. Плоская однонаправленная волна. Тензор энергии-импульса

1
( E 2 H 2 ),
8
1
U 0i
[ E H ]i ,
4
1
1
U ik
( Ei E k H i H k )
ik ( E 2 H 2 ) , i, k 1, 2, 3.
4
8
U 00 U 00
U 0i
U ik
1
E2
2
2
U W
(E H )
,
8
4
c
c
c 2
c 2
{U 0i } S
[E H ]
[E [m E]]
E m
H m cWm,
4
4
4
4
00
U ik ? i, k 1, 2,3. - дома

7. Монохроматические волны

Для монохроматических волн с круговой частотой ω
2 f
2 f .
2
t
Поэтому волновое уравнение превращается в уравнение Гельмгольца
f k 2 f 0.
k 2 ( / c) 2
Элементарное решение –
f f 0 exp[ i(k, r)].
k 2 k 2 ( / c) 2
плоская волна
Это сокращенная комплексная запись. Подразумевается Re (физические
величины вещественны). Знак Re можно опускать для линейных операций.
В общем случае k k ik
Однородные плоские волны: k – вещественный вектор, k = km.
Неоднородные плоские волны: k 0
f f 0 exp[ i(k , r)] exp[ (k , r)].
Вектор k определяет направление изменения амплитуды f, а вектор k направление нормали к (плоскому) волновому фронту. Взаимная ориентация
этих векторов: k 2 k 2 k 2 2i(k , k ) k 2 .
Произвольное начальное распределение поля может быть разложено в спектр (интеграл)
плоских волн. В общем случае возникают однородные и неоднородные плоские волны. Доля
неоднородных волн возрастает для мелкомасштабных распределений (с размерами,
сравнимыми или меньшими длины волны излучения).

8. Поляризация монохроматического излучения

Произвольное монохроматическое электромагнитное поле
локально обладает определенной поляризацией. В точке с
фиксированными координатами (коэф. не зависят от времени)
Ex A cos( t ), E y B cos( t ), Ez C cos( t )
(*)
При изменении времени конец вектора Е прочерчивает
некоторую фигуру в пространстве {Ex , E y , Ez }. Покажем, что эта
фигура плоская и лежит в плоскости, проходящей через начало
координат – точку М0 с координатами {Ex 0, E y 0, Ez 0}
Для этого покажем, что точка М с координатами (*) для
произвольного t, точка М0, точка М1 с координатами (*) при
ωt=0 и точка М2 с координатами (*) при ωt=π/2 лежат в одной
плоскости.

9. Поляризация монохроматического излучения*

(аналитич.
Ex
Det Ex E x(1)
E E (2)
x
x
Ey
Ey E
Ey E
E z E z(1) 0
E z E z(2)
Ez
(1)
y
(2)
y
геометрия)
Ex
(1)
Det E x
E (2)
x
Ey
E y(1)
E y(2)
Ez
(1)
Ez 0
E z(2)
Ex A cos( t ), E y B cos( t ), Ez C cos( t )
Ex(1) A cos , Ey(1) B cos , Ez(1) C cos
Ex(2) A sin , Ey(2) B sin , Ez(2) C sin
1
1
cos x sin y [sin( x y ) sin( x y )], sin x sin y [cos( x y ) cos( x y )]
2
2

10. Поляризация монохроматического излучения*

Направляем ось z вдоль нормали к этой плоскости
E x a1 cos( t 1 ), E y a 2 cos( t 2 ), E z 0.
Исключаем отсюда время
2 1
Ex
a1
2
Ey
a2
2
Ex E y
2
cos sin 2 ,
a1 a 2
Это соотношение относительно Ex и Ey в общем случае описывает
эллипс. С течением времени траектория, описываемая концом вектора E,
является эллипсом. Эллипс вписан в прямоугольник со сторонами,
параллельными осям x и y с длиной, соответственно, 2a1 и 2a2. Общий
случай отвечает эллиптической поляризации волны. В частных случаях
эллипс вырождается в прямую (линейная поляризация) или в круг
(круговая поляризация).

11. Параметры Стокса

Для монохроматического излучения
s0 a12 a22 , s1 a12 a22 , s2 2a1a2 cos , s3 2a1a2 sin
s02 s12 s22 s32
3 независимых параметра. s0 ~ интенсивности излучения.
Параметры Стокса удобно рассматривать как декартовы
координаты точки на сфере радиуса s0. Линейная
поляризация отвечает точкам на экваторе, а две чисто
круговые – «северному» и «южному» полюсам.
Частично поляризованное излучение
немонохроматично. Связь с частичной
когерентностью излучения. [М. Борн, Э. Вольф.
Основы оптики. Глава 10] – тема презентации

12. Интенсивность излучения

для монохроматического излучения – среднее за оптический
период значение потока энергии (вектора Пойнтинга). Для
плоской монохроматической волны
c
S
E2 m
4
Комплексная запись E Re{E0 exp(ik 0r i 0t )}
c
{E0 exp(ik 0r i 0t ) E*0 exp( ik 0r i 0t )}2 m
16
c
| E0 |2 m
8
Для немонохроматического излучения вычисляется среднее
значение за время, значительно превышающее характерный
оптический период.
S

13. Интенсивность излучения*

Несколько волн с различающимися частотами и
направлениями распространения
N
E Re En exp(ik nr i nt )
n 1
Для монохроматического излучения ( m )
N
N
1
E2 {exp( i t ) E n exp(ik nr ) exp(i t ) E*n exp( ik nr )}2
4
n 1
n 1
1 N
| En exp(ik nr ) |2
2 n 1

14. Интенсивность излучения*

Результат зависит от поляризации волн. Для двух волн (N = 2)
интерференционные члены исчезают при ортогональных
поляризациях волн. При совпадающих поляризациях –
интерференционные полосы. При большем числе волн
возможны «оптические вихри», или винтовые дислокации
волнового фронта. Тогда в поперечном сечении имеются точки,
в которых интенсивность обращается в 0, а фаза поля при
обходе вокруг таких точек получает приращение, кратное 2π.

15. Задания

1. В вакууме распространяются две волны с эл. напряженностями
E1,2 e y A exp(ik1,2r i t ), k1,2 kxe x kze z , kx2 kz2 2 / c2 .
Найти интенсивность и компоненты вектора Пойнтинга в
плоскости z = 0.
2. В вакууме магн. напряженность H = [r x h]cos(ωt). Найти Е.
Имеются ли ограничения на постоянные параметры задачи?
3. В вакууме распространяются три плоских монохроматических
волны с компланарными (лежащими в одной плоскости)
волновыми векторами, совпадающими частотами и
поляризациями и вещественными амплитудами А1, А2 и А3.
При каких условиях существуют точки, в которых
- дома
интенсивность = 0 ?
Ответ: Амплитуды волн должны удовлетворять «правилу
треугольника»: | Am An | Al Am An

16. Реализуемы ли плоские волны?

Ввиду независимости напряженностей поля плоской волны
от поперечных координат полная мощность, переносимая
такой волной, бесконечна. Поэтому одиночная плоская волна
и сумма нескольких плоских волн не отвечают физически
реализуемому излучению.
Однако в линейной электродинамике справедлив принцип
суперпозиции. Можно разложить в интеграл по плоским
монохроматическим волнам практически любое
распределение поля, обладающее конечной энергией
(мощностью). Тем самым, знание плосковолновых решений
дает принципиальную возможность решить аналогичные
задачи с реальными пучками и импульсами э-м излучения.

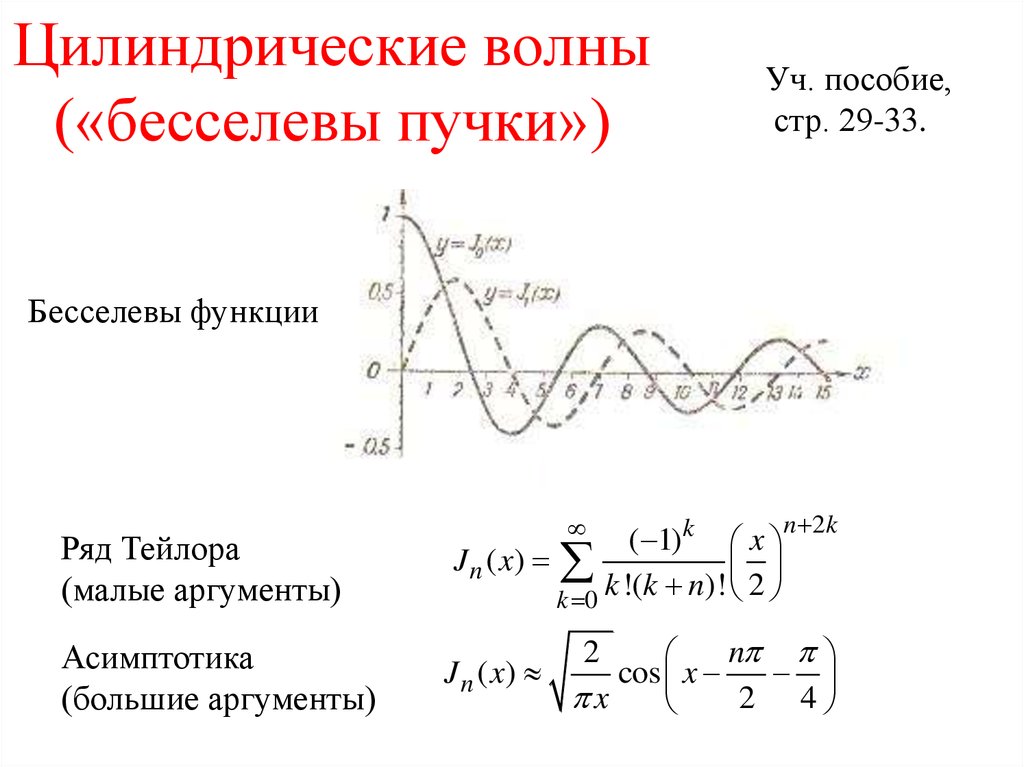
17. Цилиндрические волны («бесселевы пучки»)

Уч. пособие,
стр. 29-33.
Бесселевы функции
Ряд Тейлора
(малые аргументы)
( 1)k x
J n ( x)
k
!(
k
n
)!
2
k 0
Асимптотика
(большие аргументы)
J n ( x)
n 2 k
2
n
cos x
x
2 4

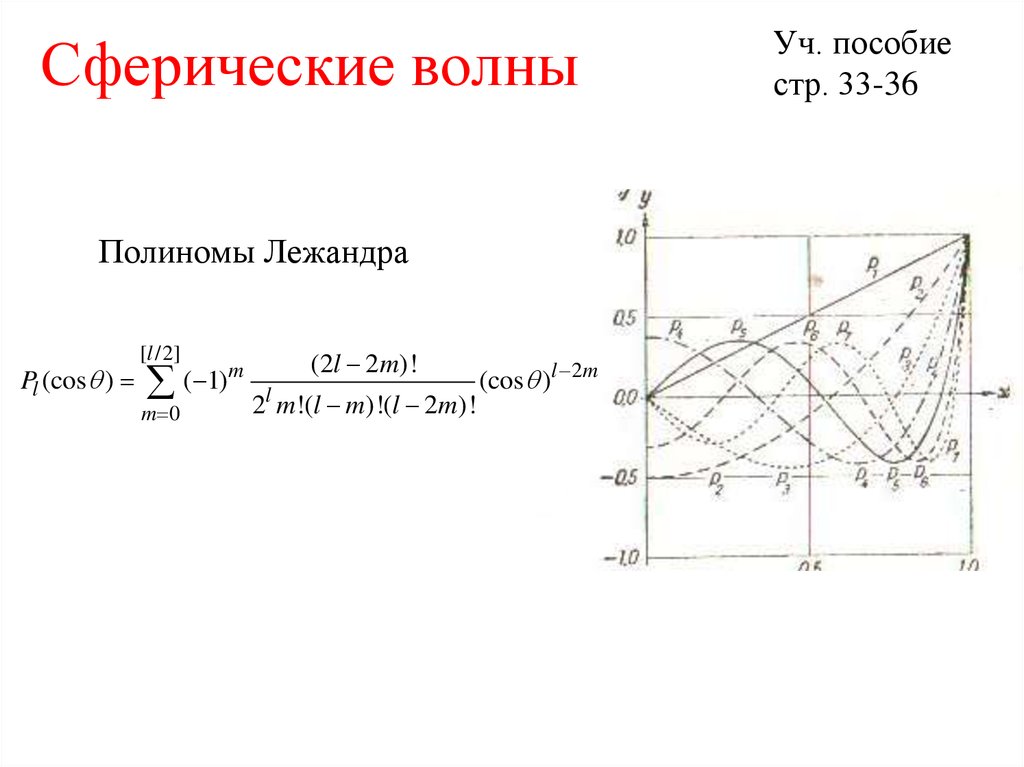
18. Сферические волны

Полиномы Лежандра
Pl (cos )
[l /2]
m 0
( 1) m
(2l 2m)!
2l m !(l m)!(l 2m)!
(cos )l 2m
Уч. пособие
стр. 33-36

19. Высокочастотная асимптотика

• Уч. пособие, стр. 36-42 (последнее
уравнение (12.20))