Системы линейных алгебраических уравнений

1. Системы линейных алгебраических уравнений:

совместность( теорема Кронекера –
Каппели), число решений, решение
методом Гаусса
1

2. Системы любого числа линейных алгебраических уравнений

О п р е д е л е н и е 1. Системой линейных алгебраических
уравнений, состоящей из m уравнений с n неизвестными
х1,…,хn, называется система вида:
a11 x1 a1n x n b1
a x a x b
21 1
2n n
2
a m1 x1 a mn x n bm ,
(1)
2

3. Системы любого числа линейных алгебраических уравнений

где a11,…,amn, b1,…,bm некоторые числа. Если b1=0,….,bm=0,
то система называется линейной однородной. В противном
случае система (1) называется линейной неоднородной
системой.
З а м е ч а н и е 1. Система (1) может быть записана в
векторной форме:
А x b ,
(2)
3

4. Системы любого числа линейных алгебраических уравнений

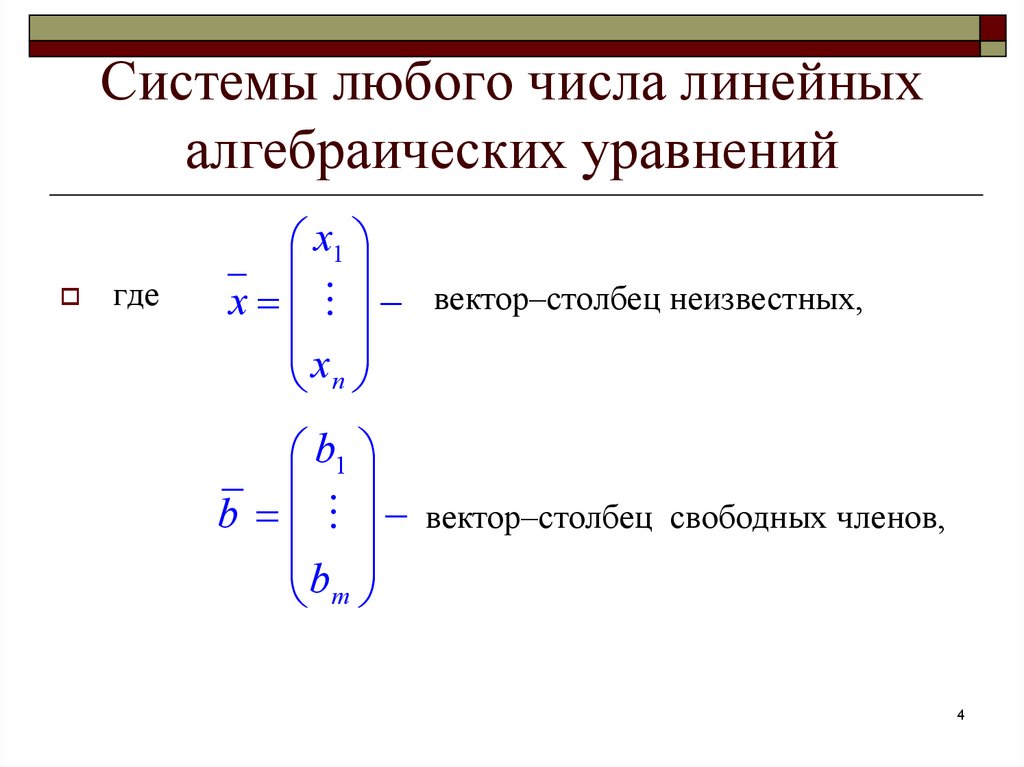
где
x1
x вектор–столбец неизвестных,
x
n
b1
b
b
m
вектор–столбец свободных членов,
4

5. Системы любого числа линейных алгебраических уравнений

a11
a 21
A
a
m1
a1n
a2n
матрица системы.
a mn
О п р е д е л е н и е 2. Расширенной матрицей системы
(1) называется матрица, обозначаемая A b и
полученная приписыванием к матрице А справа после
вертикальной черты столбца b .
5

6. Системы любого числа линейных алгебраических уравнений

a11
a21
(A| b )
am1
a1n b1
a2 n b2
...
amn bn
О п р е д е л е н и е 3. Решением системы (2) называется
любой n- мерный вектор x подстановка которого в (2)
дает тождество.
6

7. Системы любого числа линейных алгебраических уравнений

О п р е д е л е н и е 4. Система называется совместной,
если она имеет хотя бы одно решение. В противном
случае система называется несовместной.
Т е о р е м а 1. (Кронекера – Капелли). Система (1)
совместна тогда и только тогда, когда ранг матрицы
системы равен рангу расширенной матрицы, то есть:
r A r A b .
При этом если r A n, то система имеет единственное
решение; если r A n, то система имеет бесконечное
множество решений (n –число неизвестных).
7

8. Системы любого числа линейных алгебраических уравнений

Т е о р е м а 2. Решение системы А x b (2) имеет вид:
x x 0 c1 l1 c k l k ,
(3)
где x 0 частное решение линейной неоднородной
системы (2); число k, называемое числом свободных
неизвестных системы (2), вычисляется по формуле k n r A
с1 , , c k произвольные постоянные числа; l1 , , l k
постоянные n- мерные векторы, являющиеся линейно
независимыми решениями соответствующей линейной
однородной системы А x 0 .
8

9. Системы любого числа линейных алгебраических уравнений

Метод Гаусса
Для решения системы (2) с матрицей А размерности mxn и
столбцом свободных членов b нужно выполнить
следующие действия:
1) Составить расширенную матрицу А b
и привести ее
к ступенчатому виду с помощью элементарных
преобразований строк;
2) Если r A r A b , записать ответ: система несовместна.
Если r A
r A b , сделать выводы:
9

10. Системы любого числа линейных алгебраических уравнений

- система совместна,
базисными неизвестными объявить те, номера
которых совпадут с номерами базисных столбцов
ступенчатого вида матрицы А, содержащих
опорные элементы этой матрицы; остальные
неизвестные объявить свободными,
- число свободных неизвестных равно k n r A ,
- перейти к выполнению следующего шага;
-
10

11. Системы любого числа линейных алгебраических уравнений

3) Привести ступенчатую матрицу, полученную при
выполнении шага 1), к виду Гаусса;
4) Написать систему линейных уравнений,
соответствующую матрице, построенной на шаге 3),
обозначив свободные неизвестные с1 , , с k ;
5) Выразить из полученной системы базисные
неизвестные через свободные неизвестные;
6) Записать ответ, воспользовавшись или векторной
формой записи (5), или координатной формой:
x j f j c1 , c k ,
j 1, n.
11

12. Системы любого числа линейных алгебраических уравнений

З а м е ч а н и е 2. Применение метода Гаусса
не требует, чтобы матрица системы А была
квадратной и предварительного вычисления ее
определителя.
12

13. ПРИМЕРЫ

П р и м е р 1. Для системы:
2 x 3 y z 5
x y 5z 3
4 x 7 z 7
указать матрицу системы А и столбец свободных членов
Записать систему в векторной форме.
b
Р е ш е н и е. Обозначим столбец неизвестных :
13

14. ПРИМЕРЫ

x
x y
z
Тогда матрица А рассматриваемой системы составляется
из числовых коэффициентов, стоящих в системе при
неизвестных:
2 3 1
A 1 1 5
4 0 7
14

15. ПРИМЕРЫ

Столбец
b
составляется из свободных членов системы:
5
b 3
7
Поэтому систему можно переписать в векторной форме:
A x b
О т в е т:
2 3 1
5
A 1 1 5 b 3
4 0 7
7
A x b
15

16. ПРИМЕРЫ

П р и м е р 2. Исследовать на совместность систему:
x 2z 1
3 x y 1
4 x y 2 z 1.
Р е ш е н и е.
x
x y
z
1 0 2
1
А 3 1 0 , b 1
4 1 2
1
16

17. ПРИМЕРЫ

Выполним шаг 1) метода Гаусса:
1
1 0 2 1 3 4 1 0 2
A b 3 1 0 1
0 1 6 2 1
4 1 2 1
0 1 6 3
1
1 0 2
0 1 6 2 .
0 0 0 1
Следовательно:
r A 2, r A b 3
и r A
О т в е т: система несовместна.
rA b .
17

18. ПРИМЕРЫ

П р и м е р 3. Решить систему:
x 2z 1
3 x y 1
4 x y 3 z 1.
Р е ш е н и е. В данном случае имеем:
1
1 0 2
x
b 1
x y A 3 1 0
1
4 1 3
z
столбец свободных
членов.
18

19. ПРИМЕРЫ

2
1
1 0 2 1 3 4 1 0
A b 3 1 0 1
0 1 6 2 1
4 1 3 1
0 1 5 3
r A r A b 3,
2
1
1 0
n
3
,
0 1 6 2
система совместна,
0 0
1 1 6 2 решение единственн ое
19

20. ПРИМЕРЫ

1 0 0 3
1 0 0 3
0 1 0 8 1 0 1 0 8
0 0 1 1
0 0 1 1
О т в е т:
x 3;
x 3,
y 8,
z 1.
y 8; z 1.
20

21. ПРИМЕРЫ

П р и м е р 4. Исследовать на совместность и решить
систему:
x1 3x2 5 x3 7 x4 1
x 2 x 3x 2 x 4 x 0
1
2
3
4
5
x
7
x
11
x
3
x
8
x
1
1
2
3
4
5
2 x1 4 x2 6 x3 4 x4 x5 0.
21

22. ПРИМЕРЫ

1
1
1
2
Р е ш е н и е. Воспользуемся методом Гаусса: составим
матрицу А рассматриваемой системы, столбец
свободных членов b и преобразуем расширенную
матрицу ( А b ) к виду Гаусса:
0 1 1 2 1
2 3 2 4 0
0
7 11 3 8 1
0
0
4 6 4 1 0
3 5
7
7 0 1
5 8 5 4 1 2
10 16 10 8 2
10 16 10 1 2
3
5
22

23. ПРИМЕРЫ

1
0
0
0
1
1
5 8 5 4 1
0
0 0 0 0 0
0
0 0 0 7 0 1 7 0
3 5 7
0
1
0
0
0
3 5 7
0
5 8 5
4
0 0 0 1
0 0 0 0
3 5 7 0 1
5 8 5 4 1
0 0 0 0 0
0 0 0 1 0
r A r A b 3 , п 5
система имеет бесконечное
1
множество решений;
1
n r 2 число свободных
0 4
неизвестны
х;
0
х1 , х 2 , х5 базисные неизвестны е;
х , х свободные неизвестны е 23
3 4

24. ПРИМЕРЫ

1 3 5 7 0 1
1 3 5 7 0 1
1
0 5 8 5 0 1 0 1 8 5 1 0 1 5 3
0 0 0 0 1 0 5
0 0 0 0 1 0
1 0 1 5 4 0 2 5
0 1 85 1 0 15 .
0 0 0 0 1 0
24

25. ПРИМЕРЫ

О т в е т:
2 1
х1 5 5 с1 4с2
2 5
1 5
4
х 1 8 с с
1 5
8 5
1
2
1
2
5 5
или х 0 с1 1 с 2 0 .
х3 с1
0
0
1
х
с
4
2
0
0
0
х 0
5
с1 , с2 произв. пост.
25