Шеңберге байланысты теоремалар (центрлік және іштей сызылған бұрыштарды есептеу)

1.

Шеңберге байланысты
теоремалар (центрлік және іштей
сызылған бұрыштарды есептеу)

2.

Сабақтың мақсаты :
ГВ 9.2 Шеңбер хордасының қасиеттерін
дәлелдейді және қолданады (қиылысатын
хордалардың кесінділерінің көбейтіндісі туралы;
шеңбер центрінен бірдей қашықтықта жатқан
хордалар туралы), Қиылысатын хордалар туралы
теореманы біледі
ГВ 9.3
Бірдей шеңберлердің хордалары тең болады
сонда тек сонда, егер олардың
перпендикулярлары тең болса;

3.

Сабақтың мақсаттары:
«Центрлік және іштей сызылған бұрыштар»
тақырыбы бойынша теориялық білімдерді жүйелеу;
Есеп шығару дағдыларын дамыту.
Lesson objectives:
• • To systematize the theoretical knowledge on the topic
"The central and inscribed angles."
• • Improve problem solving skills

4.

Еңбек етсең ерінбей,
Тояды қарның тілебей!
Repetition is the mother of learning
Повторение – мать учения!

5. Төбесі шеңбердің ішкі нүктесінде орналасқан вертикаль бұрыштар жұбының әрқайсысы шеңбердің осы бұрыштар қабырғаларымен

шектелген доғаларының
жарым қосындысымен өлшенеді
BC B / C /
2

6. Шеңберден тысқары қиылысатын екі қиюшының арасындағы бұрыш осы бұрыш қабырғаларының арасындағы доғалардың жарым айырмасының

абсолют шамасымен
өлшенеді
1
А BC B C
2

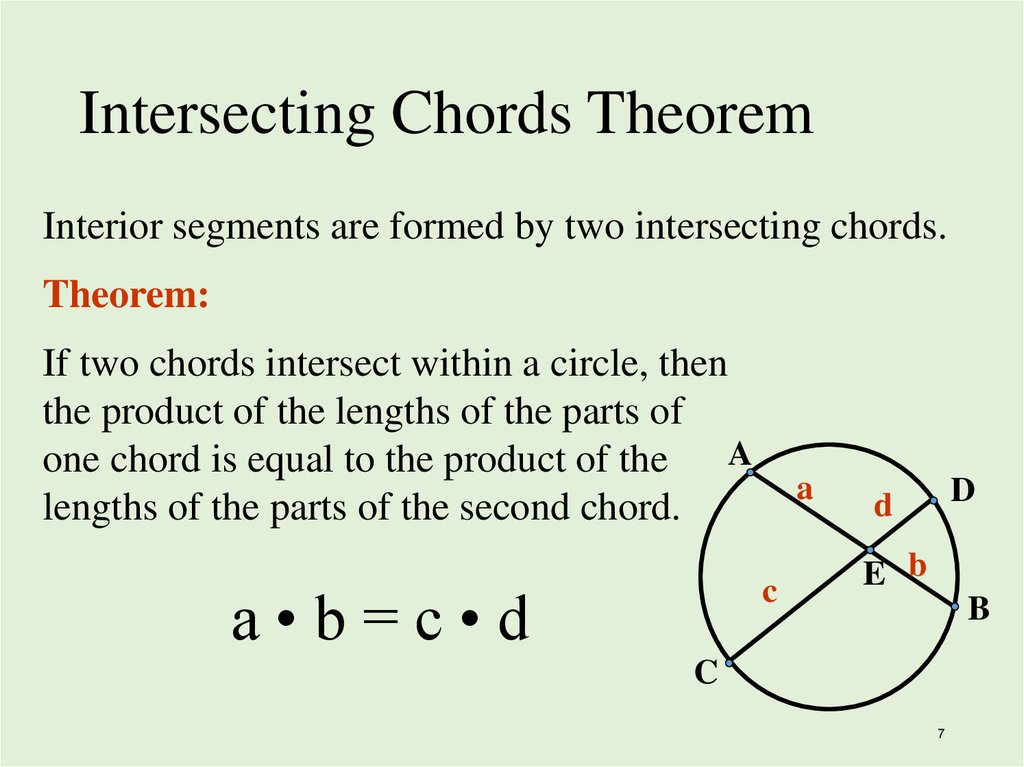
7. Intersecting Chords Theorem

Interior segments are formed by two intersecting chords.
Theorem:
If two chords intersect within a circle, then
the product of the lengths of the parts of
A
one chord is equal to the product of the
lengths of the parts of the second chord.
a
c
a•b=c•d
D
d
E b
B
C
7

8. Intersecting Secants/Tangents

Exterior segments are formed by two secants, or a secant
and a tangent.
B
A
B
C
D
A
C
D
E
Two Secants
Secant and a Tangent
8

9. Intersecting Secants Theorem

If two secant segments are drawn to a circle from an
external point, then the products of the lengths of the
secant and their exterior parts are equal.
e
A
a
B
c
b
D
C
d
a•e=c•f
f
E
9

10. Example:

In the figure; if BC 6cm, AD 2cm, AB 4cm . Find x .
A
B
C
AB AC = AD AE
4 10 = 2 (2+x)
D
40 = 4 + 2x
36 = 2x
E
X = 18 cm
10

11. Secant and Tangent Theorem:

The square of the length of the tangent equals the product
of the length of the secant and its exterior segment.
B
a2 = b • d
a
b
c
A
D
C
d
11

12. Example:

In the figure if AD 9 cm, and AC 25 cm. Find x.
AB AD AC
2
B
x 9 25
x
C
D
9 cm
2
A
x 225 15 cm
25 cm
12

13.

ЕСЕПТЕР ШЫҒАРУ
РЕШЕНИЕ ЗАДАЧ
TASKS

14.

15.

Kahoot

16. Рефлексия:

• нені білдім, нені үйрендім
• - нені толық түсінбедім
• - немен жұмысты жалғастыру қажет