Похожие презентации:
Үшбұрыштар теңдігінің белгілері
1. Үшбұрыштар теңдігінің белгілері
Сабақтың тақырыбы:Үшбұрыштар теңдігінің
белгілері
2.
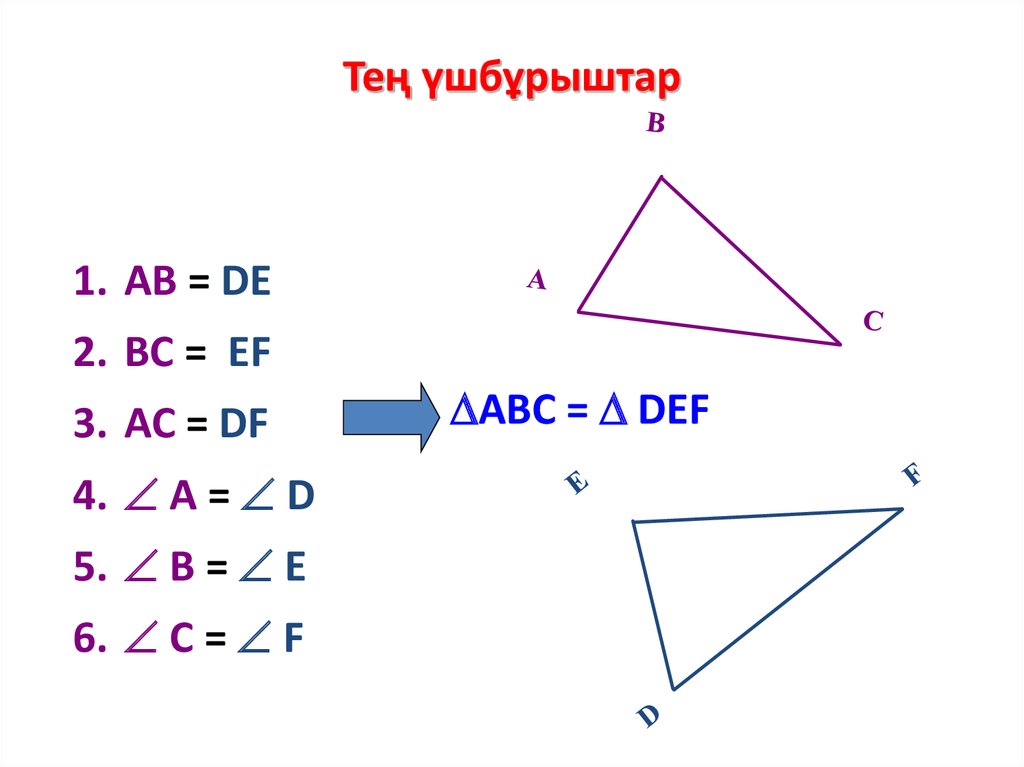
Тең үшбұрыштар1. AB = DE
2. BC = EF
3. AC = DF
4. A = D
5. B = E
6. C = F
ABC = DEF
3.
Екі үшбұрыштардың теңдігіндәлелдеу үшін барлық алты
элементтері тең болу қажет па ?
ЖОҚ!
4.
Екі үшбұрыштың теңдігінкөрсету үшін. . .
. . . кем дегенде қанша
элементтері тең болу
қажет??
5. Сабақтың мақсаты:
ГВ 8.5 үшбұрыштардың теңдік белгілеріарасындағы айырмашылықты біледі,
оларды көрсетеді және дәлелдейді
Дағдылар
Жетістік критерийлері
Білу және
түсіну
Анализ
Үшбұрыш теңдігі белгілері
арасындағы айырмашылықты көреді
Үшбұрыш теңдігі белгілері
арасындағы айырмашылықты
көрсетеді
Үшбұрыштар теңдігінің белгілерін
дәлелдейді
Синтез
6. GLOSSARY
• Congruent triangles – равные треугольники- теңүшбұрыштар
• Test of triangles equality – признаки равенства
треугольников – үшбұрыш теңдігінің белгілері
• SSS (Side Side Side) – признак равенства треугольников
по трем сторонам– үш қабырғасы бойынша (ІІІ)
үшбұрыштар теңдігінің белгісі
• SAS (Side Angle Side) – признак равенства
треугольников по двум сторонам и углу между ними–
екі қабырғасы мен арасындағы бұрышы бойынша
үшбұрыштар теңдігінің белгісі (І)
• ASA (Angle Side Angle) – признак равенства
треугольников по стороне и двум прилежащим углам–
бір қабырғасы мен іргелес екі бұрышы бойынша
үшбұрыштар теңдігінің белгісі (ІІ)
7.
Үшбұрыш теңдігінің белгілеріB1
B
І белгі Егер бір үшбұрыштың екі қабырғасы
мен олардың арасындағы бұрышы сәйкес
екінші үшбұрыштың екі қабырғасы мен
олардың арасындағы бұрышына тең болса,
онда мұндай үшбұрыштар тең болады.
ІІ белгі Егер бір үшбұрыштың бір қабырғасы
мен оған іргелес бұрыштары сәйкес екінші
үшбұрыштың бір қабырғасы мен оған іргелес
бұрыштарына тең болса, онда мұндай
A
үшбұрыштар тең болады.
A
C1
A1
B1
B
C
A1
C1
B1
B
ІІІ белгі Егер бір үшбұрыштың үш
қабырғасы екінші үшбұрыштың сәйкесінше
үш қабырғасына тең болса, онда мұндай
үшбұрыштар тең болады.
.
C
A
C
C1
A1
8.
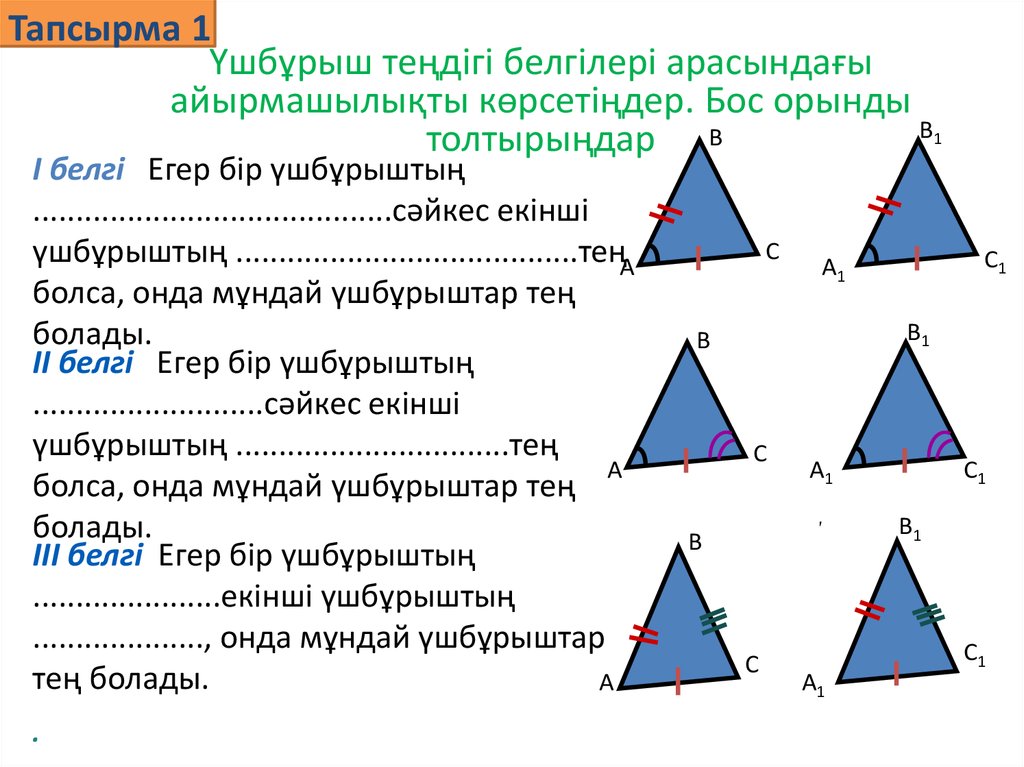
Тапсырма 1Үшбұрыш теңдігі белгілері арасындағы
айырмашылықты көрсетіңдер. Бос орынды
B1
толтырыңдар B
І белгі Егер бір үшбұрыштың
..........................................сәйкес екінші
үшбұрыштың ........................................теңA
болса, онда мұндай үшбұрыштар тең
болады.
ІІ белгі Егер бір үшбұрыштың
...........................сәйкес екінші
үшбұрыштың ................................тең
A
болса, онда мұндай үшбұрыштар тең
болады.
ІІІ белгі Егер бір үшбұрыштың
......................екінші үшбұрыштың
...................., онда мұндай үшбұрыштар
тең болады.
A
.
C
C1
A1
B1
B
C
A1
C1
B1
B
C
C1
A1
9.
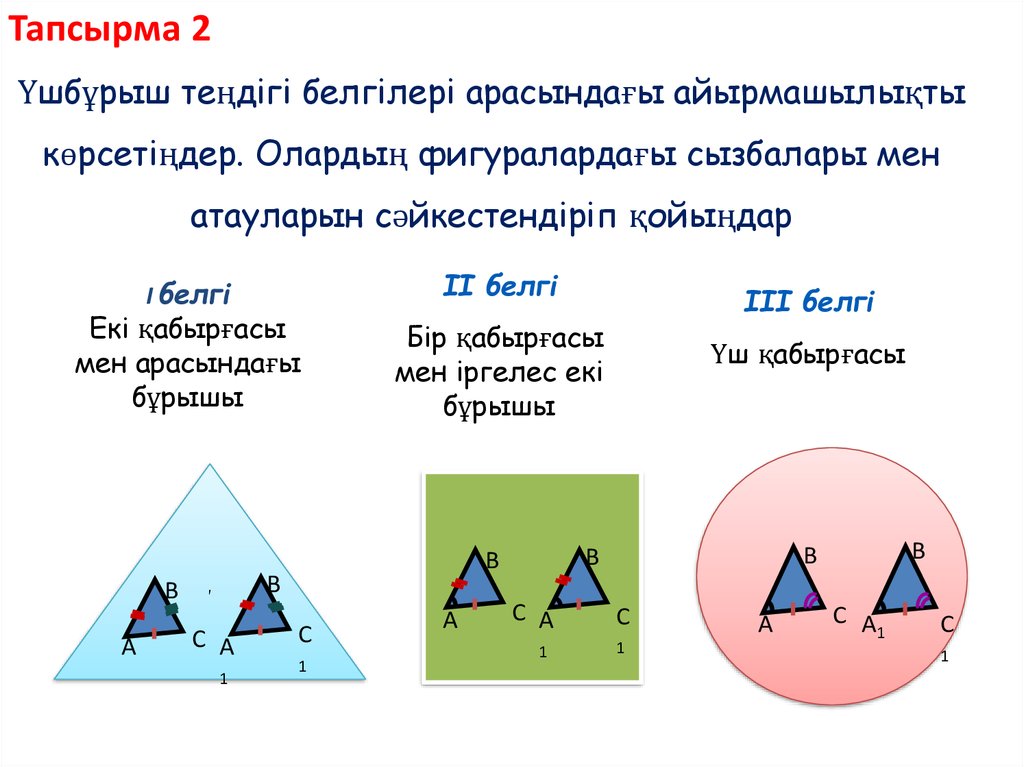
Тапсырма 2Үшбұрыш теңдігі белгілері арасындағы айырмашылықты
көрсетіңдер. Олардың фигуралардағы сызбалары мен
атауларын сәйкестендіріп қойыңдар
ІІ белгі
І белгі
Екі қабырғасы
мен арасындағы
бұрышы
1
A
Бір қабырғасы
мен іргелес екі
бұрышы
C A
1
Үш қабырғасы
B
B
B
B
B
B
ІІІ белгі
1
1
C
1
A
C A
1
C
1
A
C A
1
C
1
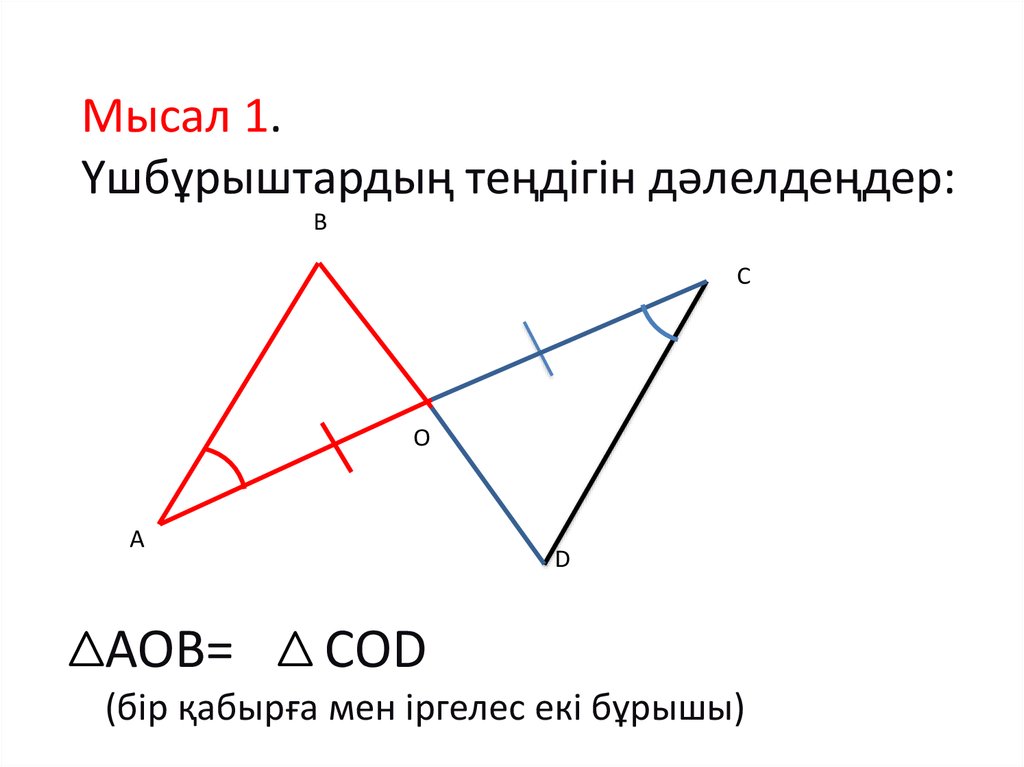
10.
Мысал 1.Үшбұрыштардың теңдігін дәлелдеңдер:
В
С
О
А
AOB=
D
COD
(бір қабырға мен іргелес екі бұрышы)
11.
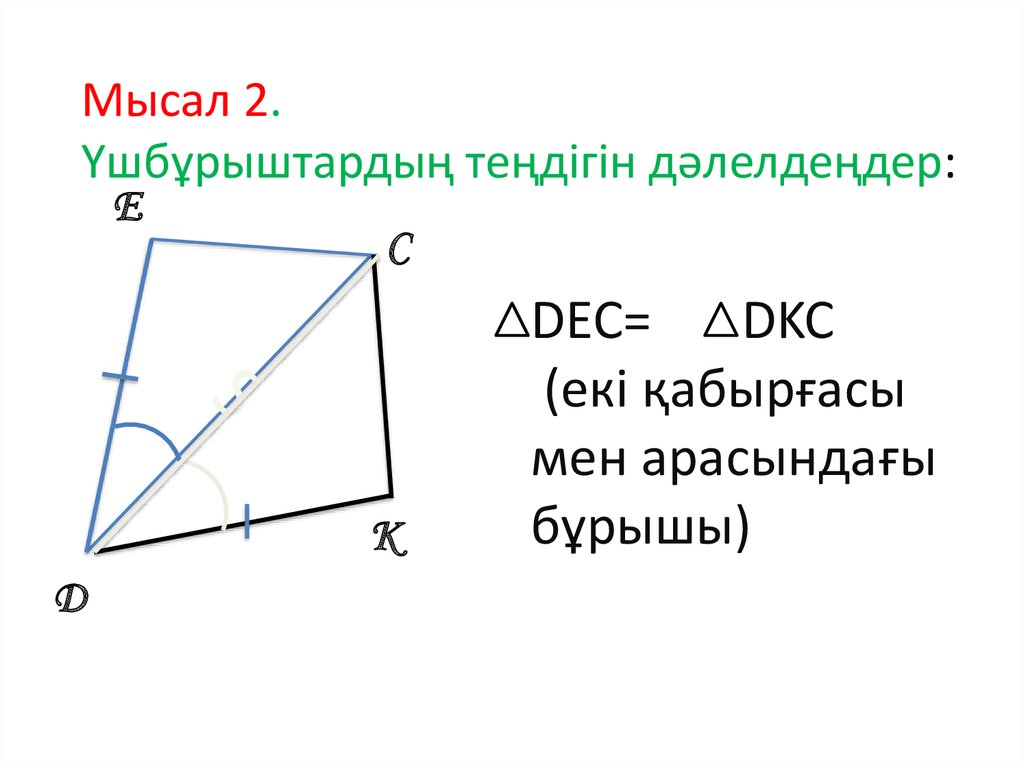
Мысал 2.Үшбұрыштардың теңдігін дәлелдеңдер:
E
C
K
D
DEC=
DKC
(екі қабырғасы
мен арасындағы
бұрышы)
12.
Мысал 3.Үшбұрыштардың теңдігін дәлелдеңдер:
ADB=
ADC
(екі қабырғасы мен арасындағы
бұрышы)
В
А
1
D
2
С
13.
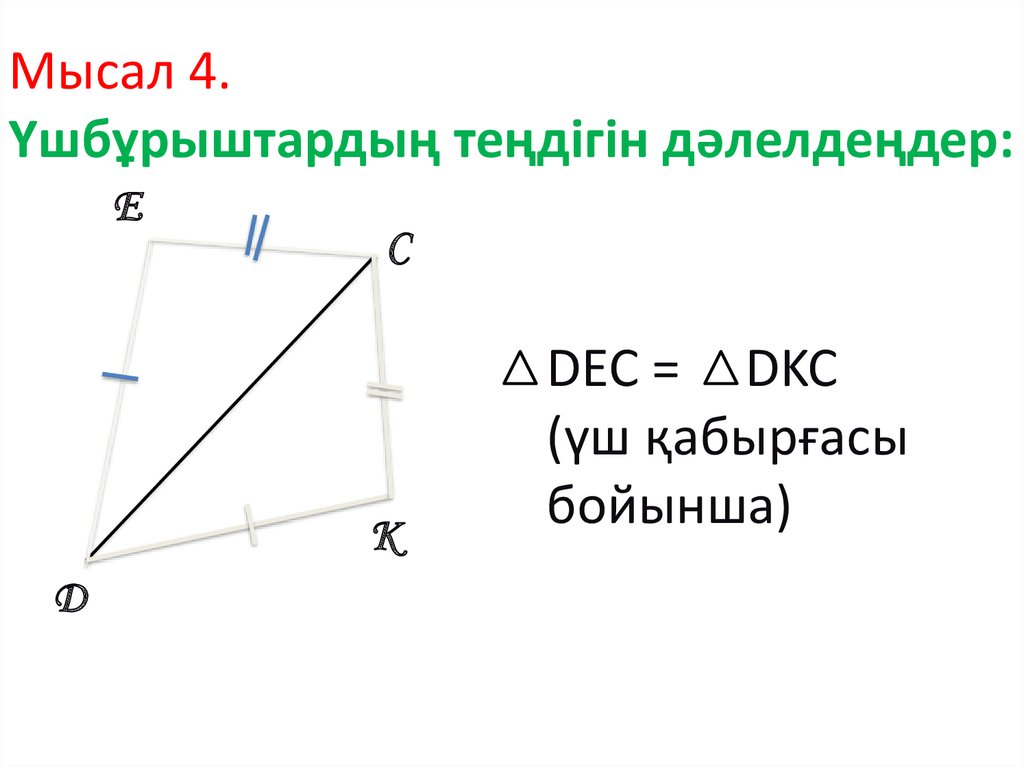
Мысал 4.Үшбұрыштардың теңдігін дәлелдеңдер:
E
C
K
D
DEC = DKC
(үш қабырғасы
бойынша)
14.
Топтық жұмыс15.
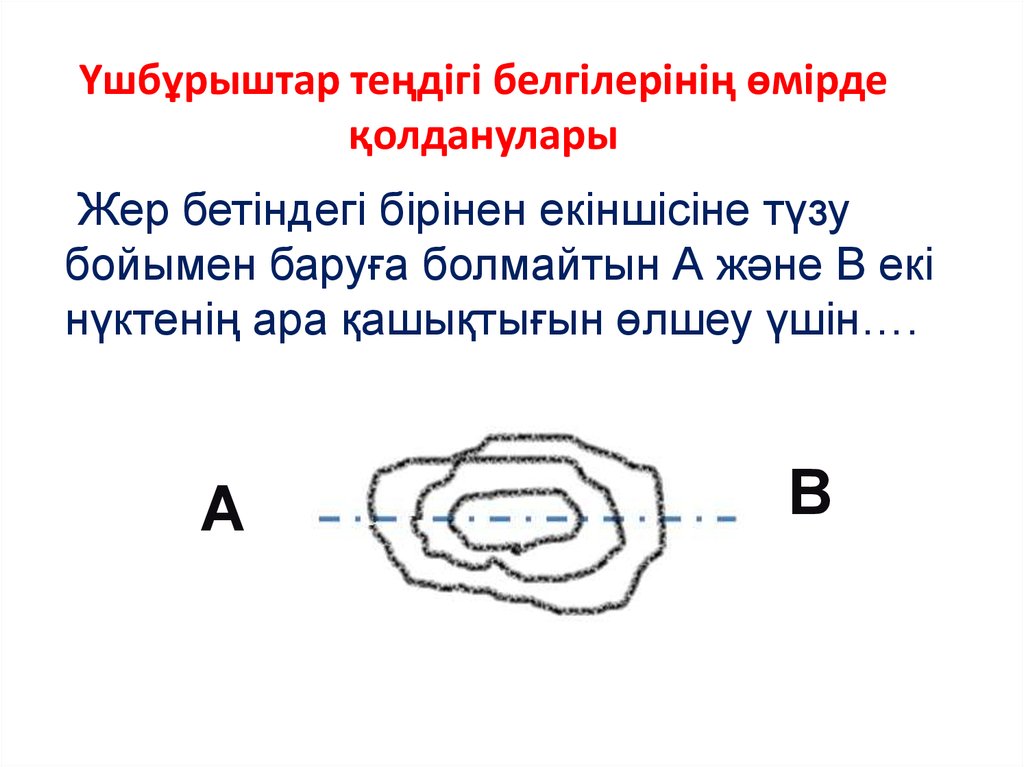
Үшбұрыштар теңдігі белгілерінің өмірдеқолданулары
Жер бетіндегі бірінен екіншісіне түзу
бойымен баруға болмайтын А және В екі
нүктенің ара қашықтығын өлшеу үшін….
А
B
16.
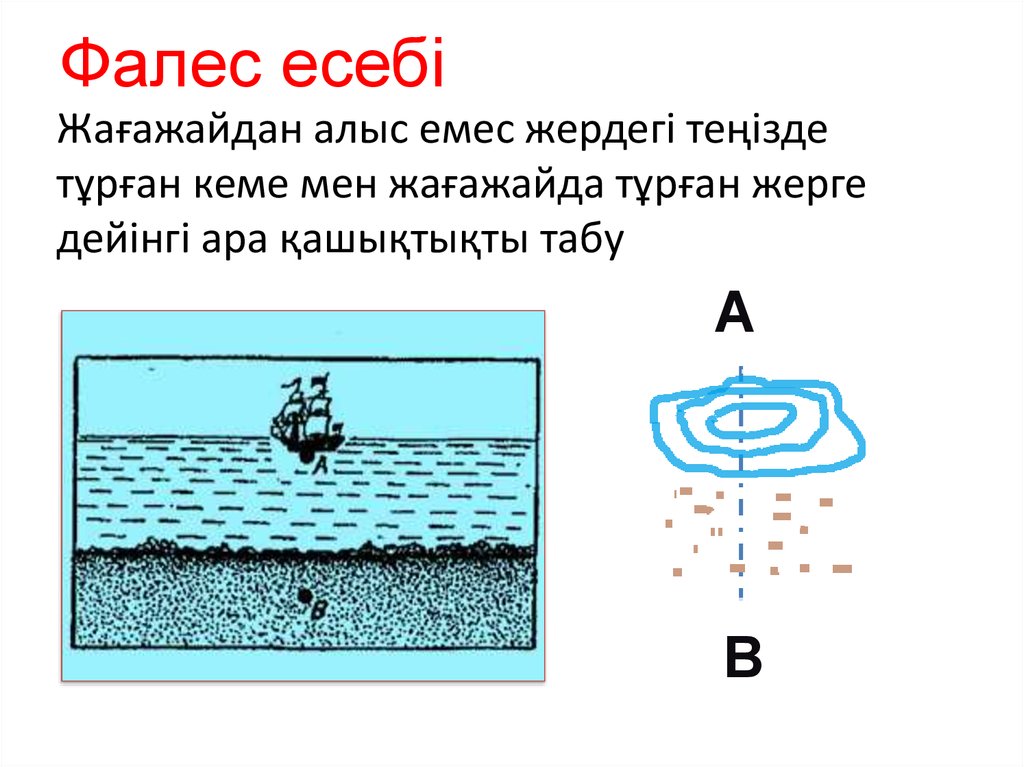
Фалес есебіЖағажайдан алыс емес жердегі теңізде
тұрған кеме мен жағажайда тұрған жерге
дейінгі ара қашықтықты табу
А
B
17.
АС
D
B
Е
Кеме A нүктесінде, ал бақылаушы B нүктесінде тұрсын
делік.
Жағажайда AB кесіндісіне перпендикуляр кез-келген
ұзындықпен BC кесіндісін саламыз, оның ортасын
табамыз (D нүктесі). E, D және A нүктелері көз
мөлшерімен қарағанда бір түзудің бойында
жататындай етіп CB кесіндісіне перпендикуляр CE
кесіндісін тұрғызамыз. Сонда AB = CE. Дәлелдеңіздер .
18. Практикалық мағынасы бар есептер
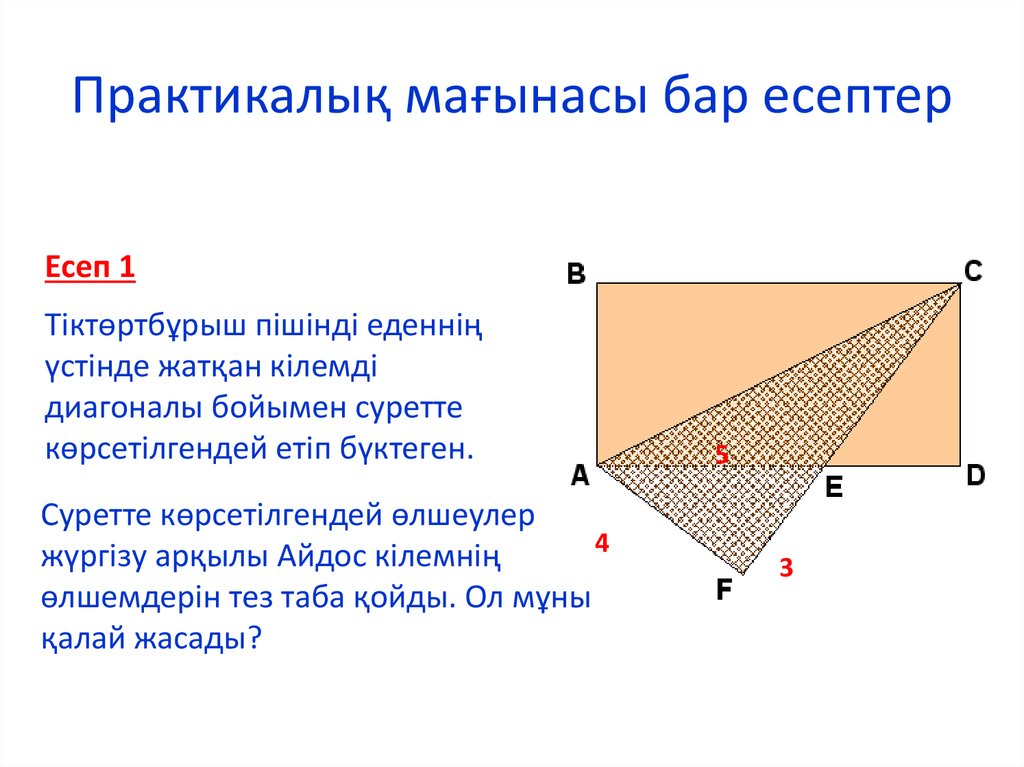
Есеп 1Тіктөртбұрыш пішінді еденнің
үстінде жатқан кілемді
диагоналы бойымен суретте
көрсетілгендей етіп бүктеген.
Суретте көрсетілгендей өлшеулер
4
жүргізу арқылы Айдос кілемнің
өлшемдерін тез таба қойды. Ол мұны
қалай жасады?
5
3
19. Есепті шешуге нұсқаулық
CB
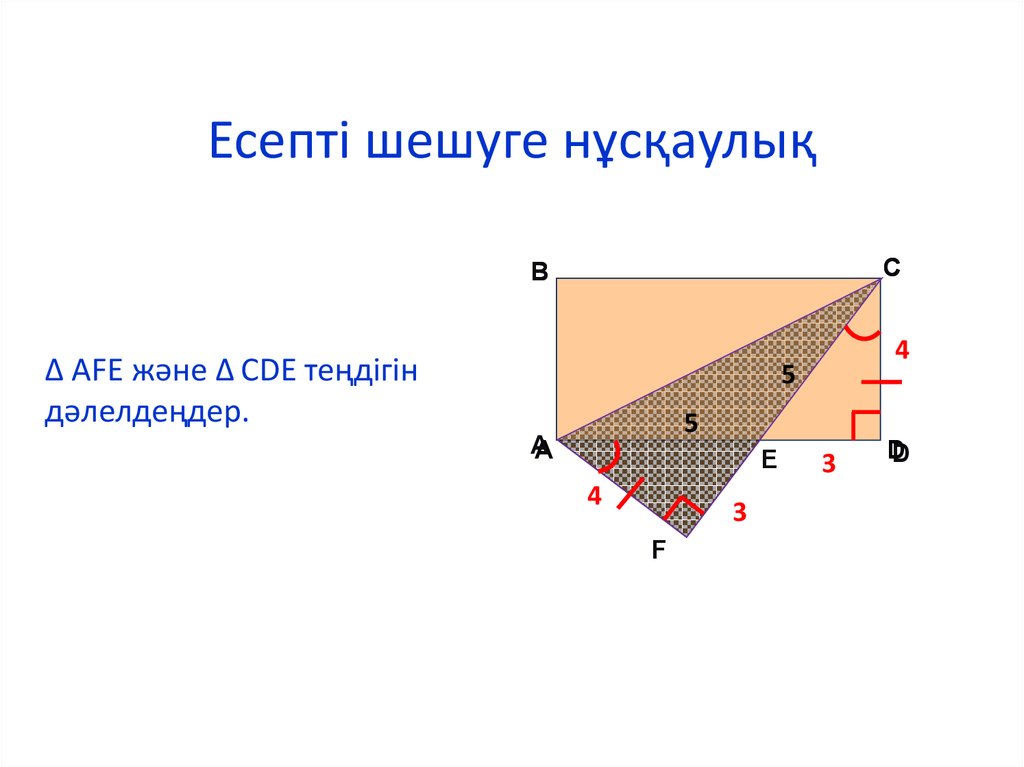
∆ AFE және ∆ CDE теңдігін
дәлелдеңдер.
4
5
5
A
A
E
4
3
F
3
D
D
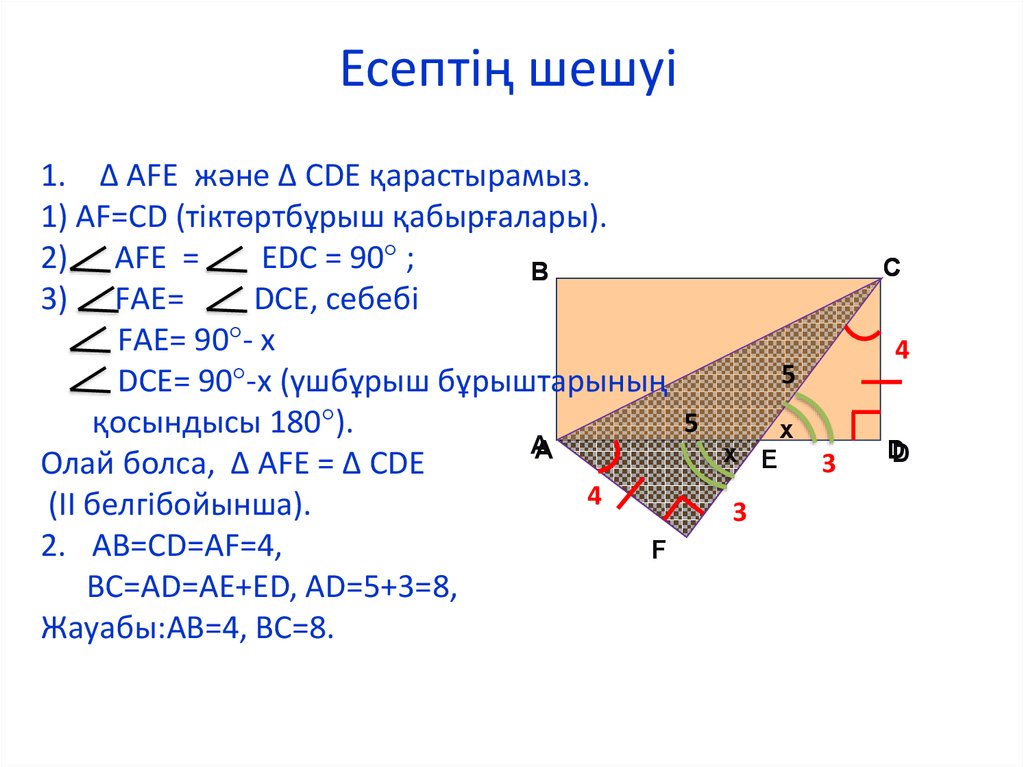
20. Есептің шешуі
1. ∆ АFЕ және ∆ СDE қарастырамыз.1) АF=СD (тіктөртбұрыш қабырғалары).
2) АFЕ =
ЕDС = 90° ;
B
3) FАЕ=
DСЕ, себебі
FАЕ= 90°- х
5
DСЕ= 90°-х (үшбұрыш бұрыштарының
5
қосындысы 180°).
х
A
A
х E
3
Олай болса, ∆ АFЕ = ∆ СDE
4
(ІІ белгібойынша).
3
2. АВ=CD=АF=4,
F
ВС=AD=AЕ+ED, AD=5+3=8,
Жауабы:АВ=4, ВС=8.
C
4
D
D
21. Практикалық мағынасы бар есептер
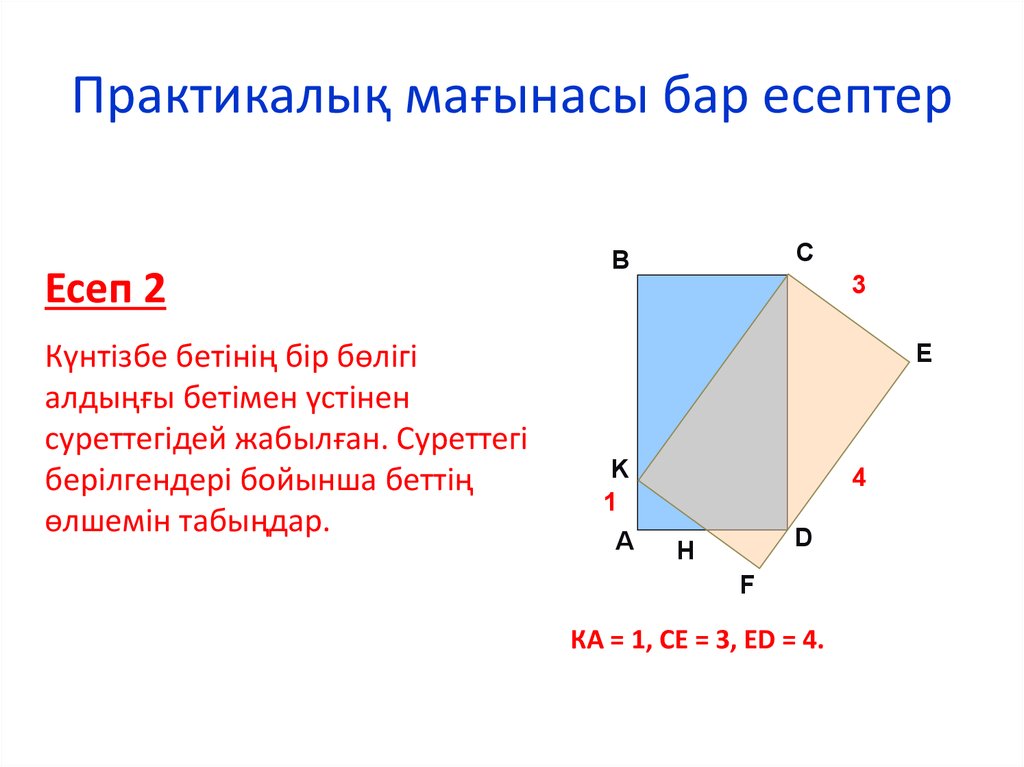
Есеп 2Күнтізбе бетінің бір бөлігі
алдыңғы бетімен үстінен
суреттегідей жабылған. Суреттегі
берілгендері бойынша беттің
өлшемін табыңдар.
C
B
3
E
K
1
A
4
D
Н
F
КА = 1, СЕ = 3, ED = 4.









 Математика
Математика








