Matem_AG_v_R3_chast1

1. Аналитическая геометрия

Тема 1
Плоскость и прямая в пространстве

2.

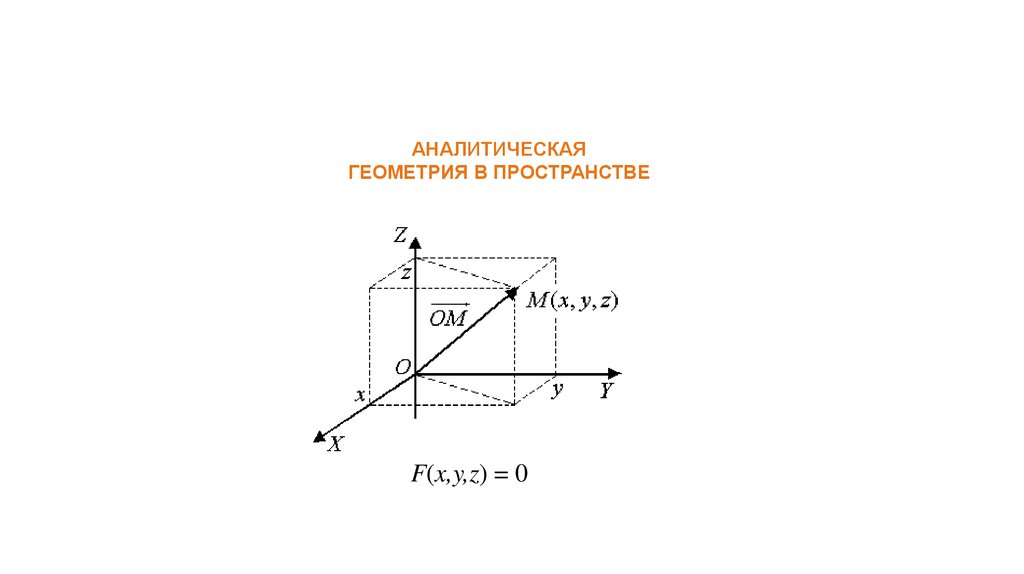
АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
F(x,y,z) = 0

3.

• Расстояние между двумя точками.
M 1 M 2 ( x2 x1 ) 2 ( y 2 y1 ) 2 ( z2 z1 ) 2
• Деление отрезка в данном отношении
y1 y 2
y
1
x1 x2
x
1
z1 z 2
z
1
Координаты середины отрезка
x
x1 x 2
2
y
y1 y 2
2
z
z1 z 2
2

4. 1. Плоскость в пространстве

5.

Плоскость в пространстве и ее уравнения
1) Уравнение плоскости, проходящей через данную точку
перпендикулярно данному вектору
M(x, y, z) – произвольная точка на плоскости P;
M0(x0, y0, z0) – данная точка на плоскости P.
M 0 M {x x0 , y y0 , z z0 }
N { A; B; C} – вектор, перпендикулярный плоскости.
Вектор N принято называть нормальным вектором плоскости.
Точка M(x, y, z) будет лежать на плоскости, если M 0 M n . Уравнение плоскости определяется
условием ( M 0 M n ) 0
A( x x0 ) B( y y 0 ) C ( z z 0 ) 0
2) Общее уравнение плоскости
Ax By Cz D 0

6.

Пример.
Составьте уравнение плоскости, проходящей
M(1;1;1) перпендикулярно к вектору N={2;2;3}.
Решение:
2 x 1 2 y 1 3 z 1 0
2 x 2 y 3z 7 0
через
точку

7.

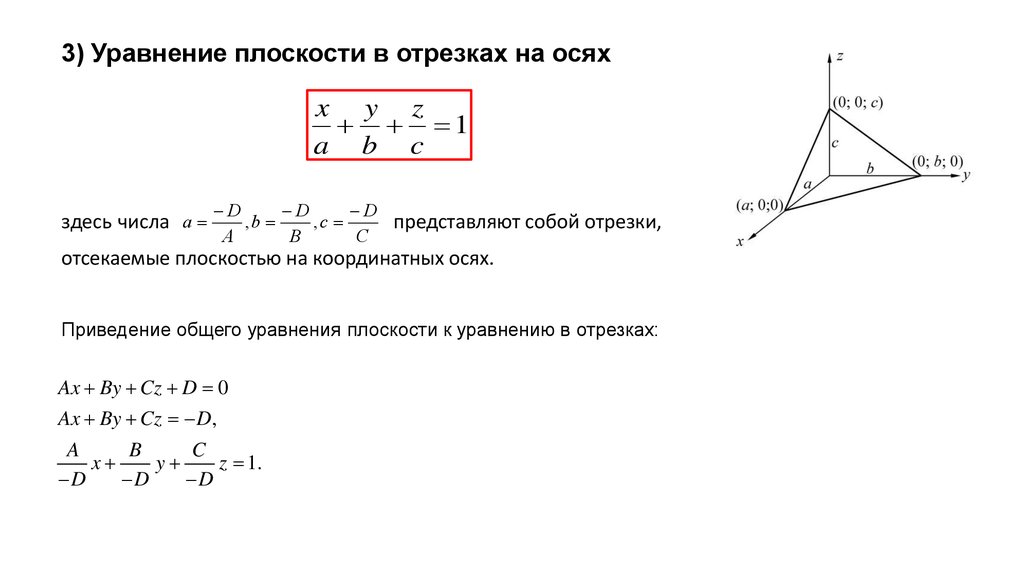
3) Уравнение плоскости в отрезках на осях
x y z
1
a b c
здесь числа a
D
D
D
,b
,c
представляют собой отрезки,
A
B
C
отсекаемые плоскостью на координатных осях.
Приведение общего уравнения плоскости к уравнению в отрезках:
Ax By Cz D 0
Ax By Cz D,
A
B
C
x
y
z 1.
D
D
D

8.

Задача.
Какие отрезки отсекает на осях координат плоскость
2x – 4y + 6z –12 = 0 ?
Решение: Приведем общее уравнение плоскости к виду
уравнения «в отрезках»:
2x 4 y 6z
x y z
1
1
12 12 12
6 3 2
Ответ: отрезки, отсекаемые на осях: a = 6, b = –3, c = 2.

9.

4) Уравнение плоскости, проходящей через три данные точки
М
x x1
y y1
x 2 x1
y 2 y1 z 2 z1 0
x3 x1
y 3 y1
Даны три точки: M 1 ( x1 ; y1 ; z1 ),
z z1
z 3 z1
M 2 ( x2 ; y2 ; z2 ), M 3 ( x3 ; y3 ; z3 ).
М1
М2
М3
M x, y,z – произвольная точка плоскости.
Точка М принадлежит плоскости M 1 M 2 M 3
в том и только в том случае, если компланарны векторы:
M 1M ( x x1 ; y y1 ; z z1 ),
M 1M 2 ( x2 x1 ; y2 y1 ; z2 z1 ),
M 1M 3 ( x3 x1 ; y3 y1 ; z3 z1 ).
Условие компланарности
M M , M M
1
1
2 , M 1M 3
0 в координатной форме и дает искомое уравнение.

10.

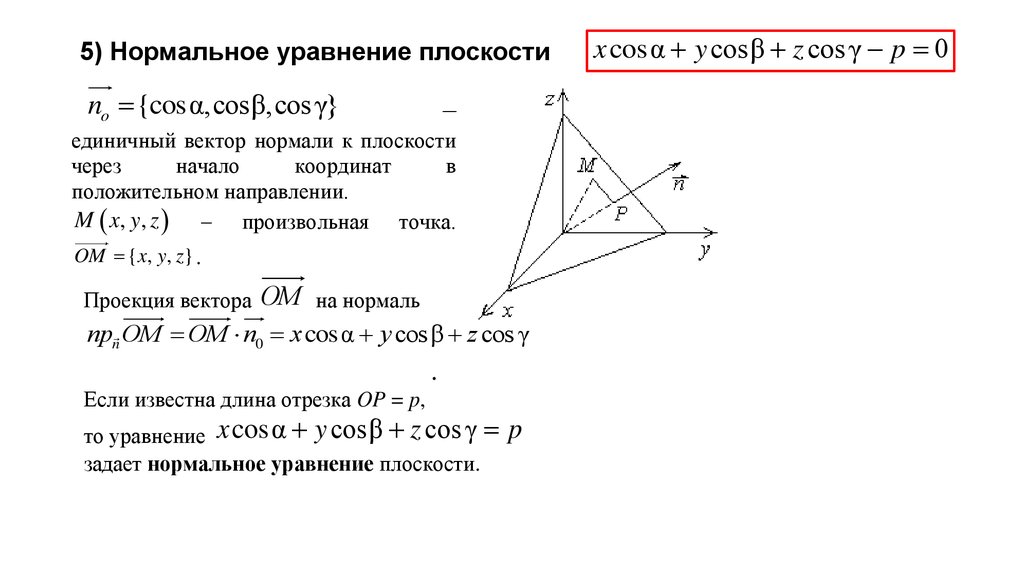
5) Нормальное уравнение плоскости
no {cosα,cosβ,cos γ}
–
единичный вектор нормали к плоскости
в
координат
начало
через
положительном направлении.
M x, y, z – произвольная точка.
OM {x, y, z} .
Проекция вектора
OM на нормаль
прn OM OM n0 x cos α y cosβ z cos γ
.
Если известна длина отрезка OP = p,
то уравнение x cosα y cosβ z cos γ
задает нормальное уравнение плоскости.
p
x cosα y cosβ z cos γ p 0

11.

Приведение общего уравнения плоскости к нормальному уравнению
μ
1
A2 B 2 C 2 – нормирующий множитель,
знак которого должен быть противоположен знаку D.
Общее уравнение плоскости приводится к нормальному
виду домножением на нормирующий множитель:
μAx μBy μCz μD 0.

12.

А=0: By + Cz + D = 0 (отсутствует переменная х) – плоскость параллельна оси Ох;
В=0: Ax + Cz + D = 0 (отсутствует переменная у) – плоскость параллельна оси Оу;
С=0: Ax + By + D = 0 (отсутствует переменная z) – плоскость параллельна оси Оz;
D=0: Ax + By + Cz = 0 – плоскость проходит через начало координат;
А=В=0: Cz + D = 0 – плоскость параллельна плоскости хОу;
А=С=0: By + D = 0 – плоскость параллельна плоскости хОz;
В=С=0: Ax + D = 0 – плоскость параллельна плоскости yOz;
А=D=0 – плоскость проходит через ось Ох;
В=D=0 – плоскость проходит через ось Оу;
С=D=0 – плоскость проходит через ось Oz;
А=В=D=0: Cz = 0 – плоскость совпадает с плоскостью хОу;
А=С=D=0: By = 0 – плоскость совпадает с плоскостью xOz;
В=С=D=0: Ax = 0 – плоскость совпадает с плоскостью yOz.

13. Условие перпендикулярности и параллельности плоскостей

1 2 , если N1 N2 (Критерий ортогональности: скалярное произведение = 0)
A1 A2 B1 B2 C1C2 0
1 2 , если N1 N2 (Критерий коллинеарности: их координаты пропорциональны или
их векторное произведение равно нулю)
A1 B1 C1
=
=
.
A2 B2 C2

14. Пример.

Составить уравнение плоскости, которая проходит через точку
M(7,-2, 3) параллельно плоскости y – 3z + 5 = 0.
Решение. Из уравнения известной плоскости N={0,1,-3}. По
условию плоскости параллельны. Значит,
A = 0, B = 1, C = – 3.
Уравнение искомой плоскости
0 ( x 7) 1 ( y 2) 3 ( z 3) 0 y 3 z 11 0

15. Пример.

Составить уравнение плоскости, которая проходит через начало
координат перпендикулярно к двум плоскостям:
x – y + 2z – 5 = 0,
2x + y – 3z + 1 = 0.
Решение. Из уравнений заданных плоскостей имеем
N1 (1, 1,2),
N 2 ( 2,1, 3),
требуется найти координаты нормали искомой плоскости:
N ( A, B, C ) ?

16.

1 способ:
N1 N 0 A B 2C 0
A 1, B 7, C 3.
N 2 N 0 2 A B 3C 0
2 способ:
i
j
N N1 N 2 1 1
2
1
k
2 (1,7,3).
3
Подставляя координаты точки (по условию – начало координат (0,0,0)) и координаты
нормального вектора в уравнение плоскости, проходящей через данную точку
перпендикулярно данному вектору, получаем искомое уравнение:
x + 7y + 3z = 0.

17. Условие совпадения (слияния) плоскостей

Если два уравнения
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
определяют одну
пропорциональны
и
ту
же
A1 B1 C1 D1
A2 B2 C2 D2
плоскость,
то
коэффициенты
их

18.

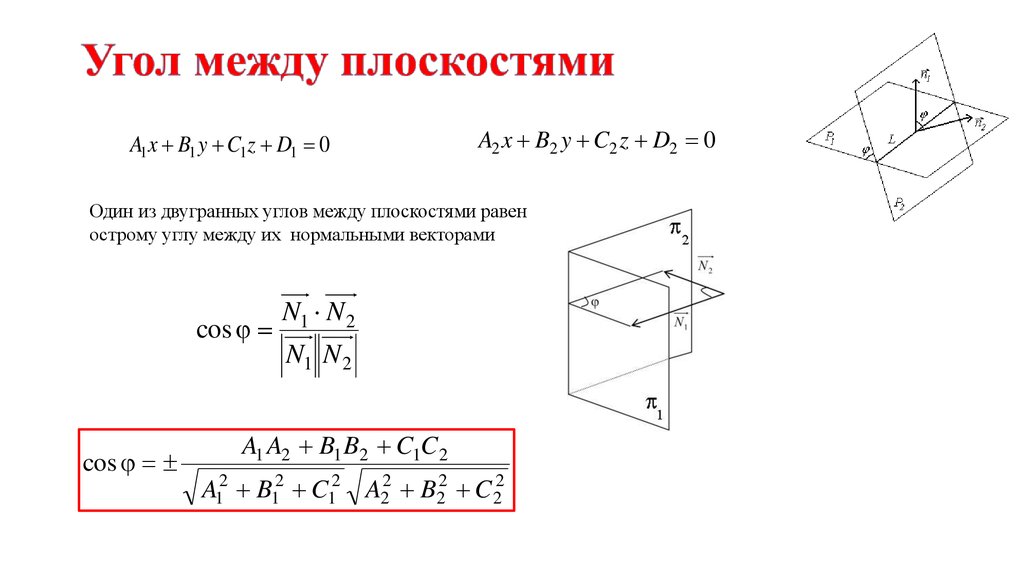
A1x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
Один из двугранных углов между плоскостями равен
острому углу между их нормальными векторами
cos
N1 N 2
N1 N 2
cos
A1 A2 B1 B2 C1C 2
A12 B12 C12 A22 B22 C 22

19.

Пример. Найти угол между плоскостями
x y 2 z 6 0, y 0.
n2 {0,1,0}
n1 {1, 1, 2}
1 0 1 1 2 0
cos
2
1 1 2 02 12 02
2
2
1
60
2

20.

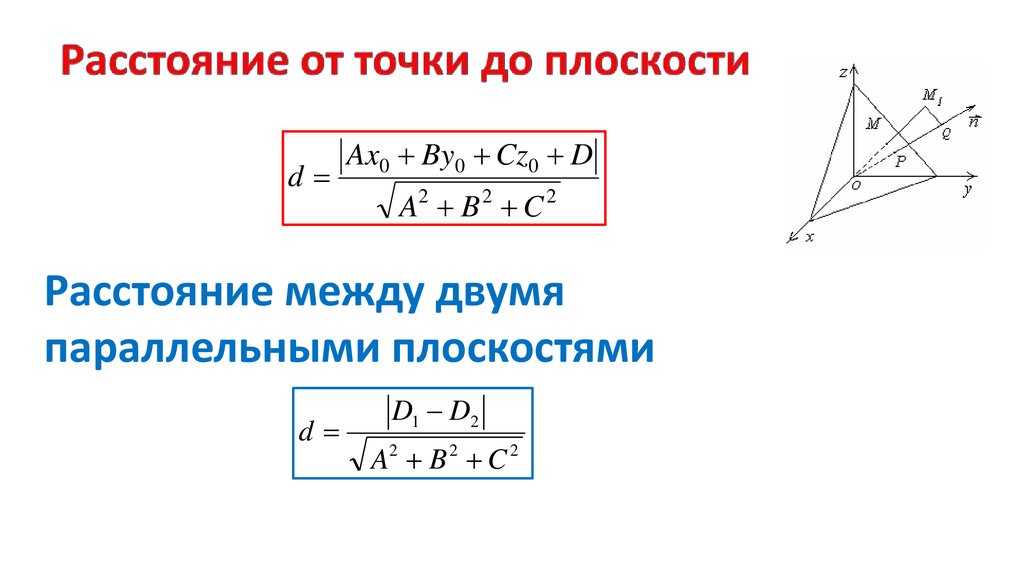
d
Ax0 By0 Cz0 D
A2 B 2 C 2
Расстояние между двумя
параллельными плоскостями
d
D1 D2
A2 B 2 C 2

21.

Пример
Найдите расстояние точки M(4, 3, 1) от плоскости
3x – 4y + 12z + 14 = 0.
d
3 4 4 3 12 1 14
3 4 12
2
2
2
2.

22. Прямая в пространстве

23.

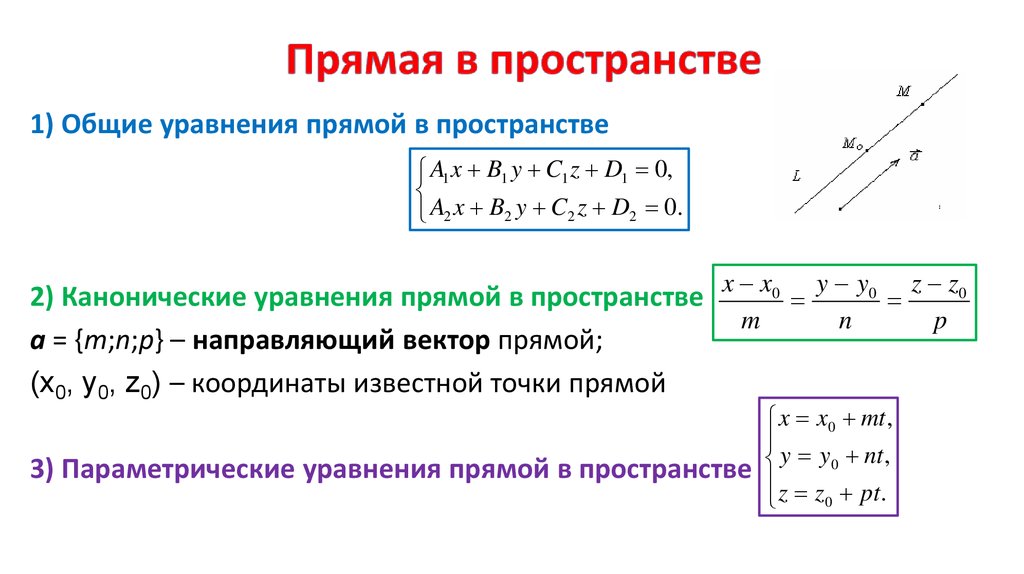
1) Общие уравнения прямой в пространстве
A1 x B1 y C1 z D1 0,
A2 x B2 y C2 z D2 0.
2) Канонические уравнения прямой в пространстве x x0 y y0 z z0
m
n
p
a = {m;n;p} – направляющий вектор прямой;
(x0, y0, z0) – координаты известной точки прямой
3) Параметрические уравнения прямой в пространстве
x x0 mt ,
y y0 nt ,
z z pt.
0

24. Пример.

Составьте канонические и параметрические уравнения прямой
3x 2 y 4 z 11 0,
2 x y 3z 1 0.
Решение. 1) Находим координаты точки, лежащей на прямой. Для этого
положим x0 1 , а две другие координаты найдем из системы:
3 2 y0 4 z0 11 0 y0 2
M 0 (1, 2,1).
2 y0 3z0 1 0
z0 1

25.

2) Находим направляющий вектор прямой:
N1 (3,2,4), N 2 ( 2,1, 3),
i
j
a N1 N 2 3 2
k
4 i
2 1 3
2
4
1 3
j
3
4
2 3
k
3 2
2 1
10i 17 j k ,
a ( 10,17, 1).
3) Канонические уравнения прямой:
x 1 y 2 z 1
10
17
1
x 1 10t ,
Параметрические уравнения прямой: y 2 17t ,
z 1 t.

26.

4) Уравнение прямой в пространстве,
проходящей через две данные точки
x x1
y y1
z z1
x2 x1 y 2 y1 z2 z1
M1 ( x1 , y1 , z1 ) и M 2 ( x2 , y2 , z2 ) - известные точки на прямой;
M ( x, y, z ) - произвольная точка прямой.
M 1M 2 ( x2 x1 ; y2 y1 ; z2 z1 ) ( m; n; p ) – направляющий вектор.
Угол между двумя прямыми в пространстве определяется углом
между их направляющими векторами
L1
L2
l1 l2
m1m2 n1n2 p1 p2
cos
l1 l2
m12 n12 p12 m22 n22 p22

27.

Пример.
Составьте уравнение прямой, проходящей через две точки M1 (1, - 2,1) и
M 2 (3,1, - 1).
Решение
x 1 y 2 z 1
x 1 y 2 z 1
.
3 1 1 2 1 1
2
3
2

28.

Пример.
Определите угол между двумя прямыми:
3 x 4 y 2 z 0,
L1 :
2 x y 2 z 0,
4 x y 6 z 2 0,
L2 :
y 3 z 2 0.

29.

Решение.
Прямые задаются пересечением плоскостей:
L1 : N1 (3, 4, 2), N 2 ( 2,1, 2),
L2 : N 3 ( 4,1, 6), N 4 (0,1, 3).
Направляющие векторы прямых:
i
j
k
2
1
2
i
j
k
a 1 N1 N 2 3 4 2 10i 2 j 11k ,
a 2 N 3 N 4 4 1 6 3i 12 j 4k .
0 1 3

30.

10 3 2 12 11 4
98
cos
;
102 22 112 32 122 42 195
98
arccos
.
195

31.

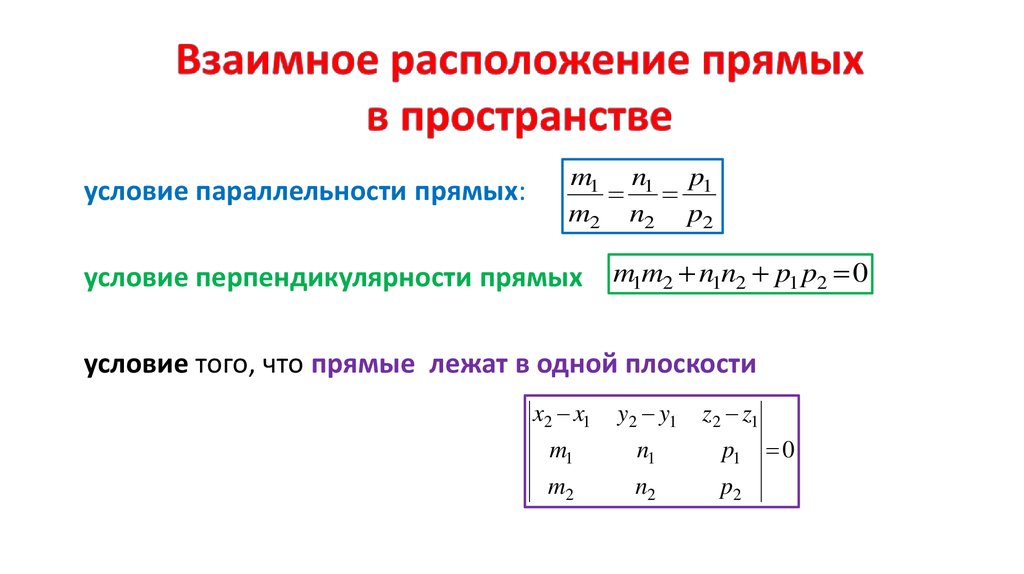
условие параллельности прямых:
m1 n1 p1
m2 n2 p2
условие перпендикулярности прямых
m1m2 n1n2 p1 p2 0
условие того, что прямые лежат в одной плоскости
x2 x1
y2 y1
z2 z1
m1
n1
p1
m2
n2
p2
0

32.

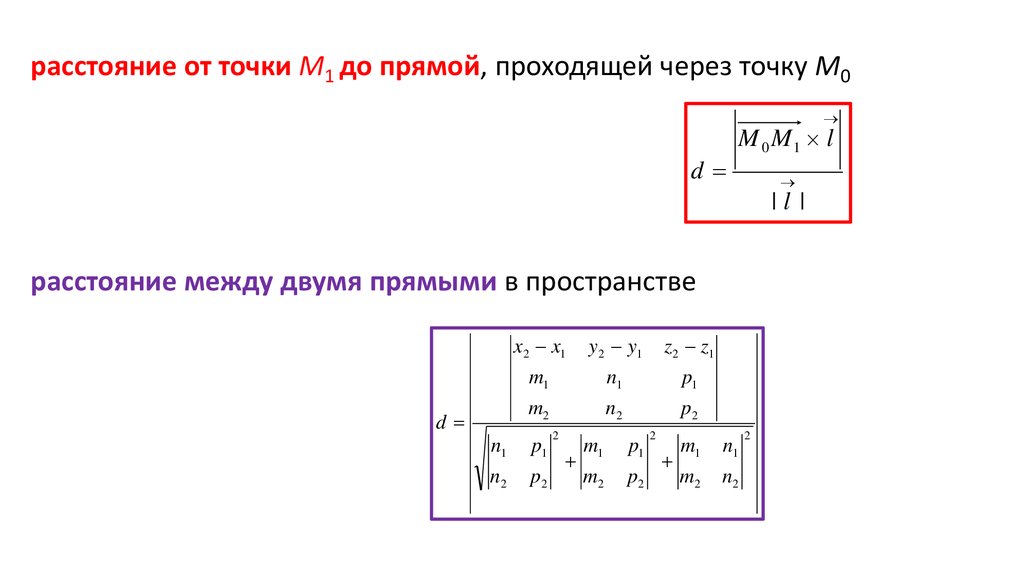
расстояние от точки М1 до прямой, проходящей через точку М0
d
M 0M1 l
|l |
расстояние между двумя прямыми в пространстве
d
x2 x1
y 2 y1
z2 z1
m1
n1
p1
m2
n2
p2
n1
p1
n2
p2
2
m1
p1
m2
p2
2
m1
n1
m2
n2
2

33.

ПРЯМАЯ И ПЛОСКОСТЬ

34.

Точка пересечения прямой и плоскости
Пример.
x 1 y 1 z
Найдите точку пересечения прямой L :
1
2 6
и плоскости
: 2 x 3 y z 1 0.
Решение. 1) Запишем уравнение прямой в параметрическом виде:
x 1 t,
x 1 y 1 z
L:
t y 1 2t ,
1
2
6
z 6t.

35.

2) Подставим выражения для переменных x, y, z в уравнение
плоскости и найдем значение параметра t
: 2 x 3 y z 1 0.
2(t 1) 3( 2t 1) 6t 1 0 t 1,
3) Найденное значение параметра t подставим в параметрические
уравнения прямой и получим искомые координаты точки пересечения:
x 2,
y 3,
z 6.

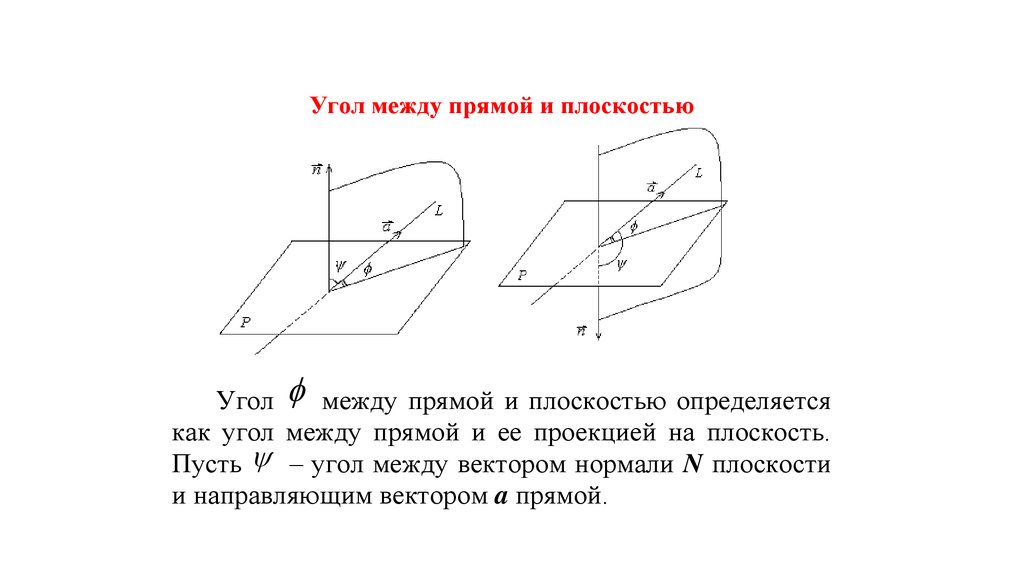
36.

Угол между прямой и плоскостью
Угол между прямой и плоскостью определяется
как угол между прямой и ее проекцией на плоскость.
Пусть – угол между вектором нормали N плоскости
и направляющим вектором a прямой.

37.

Если угол острый, то ; если угол тупой, то ,
2
2
то есть
2
.
sin sin
2
cos
n a
n a

38.

условие параллельности l
Am Bn Cp 0 и Ax0 By0 Cz0 D 0.
условие того, что прямая принадлежит плоскости l
Am Bn Cp 0 и Ax0 By0 Cz0 D 0.
A B C
условие параллельности l
m n p

39.

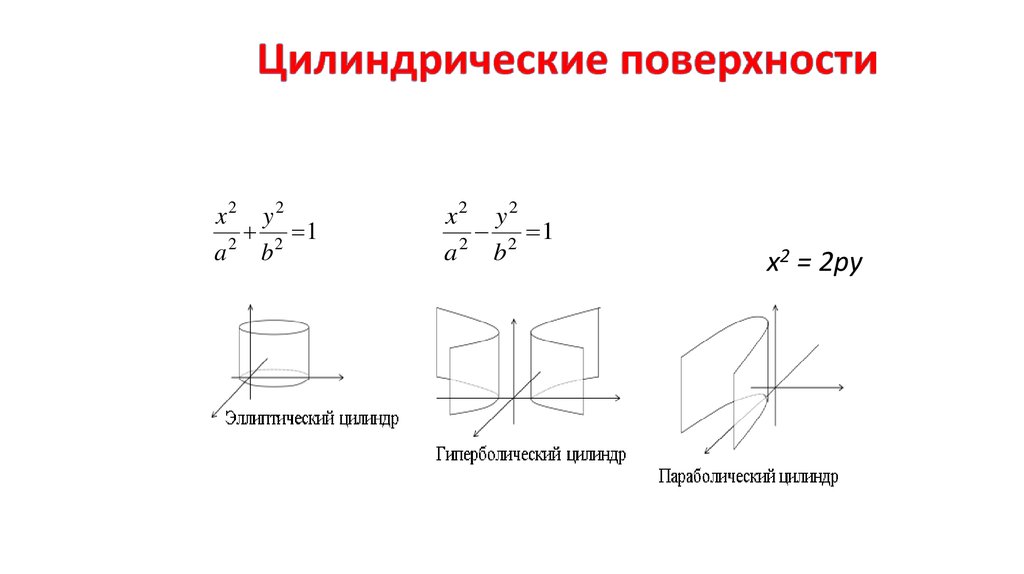
x2 y2
2 1
2
a b
x2 y2
2 1
2
a b
x2 = 2py