Теоретические методы в морской ледотехнике

1.

Федеральное государственное унитарное предприятие
«КРЫЛОВСКИЙ ГОСУДАРСТВЕННЫЙ НАУЧНЫЙ ЦЕНТР»
СОВРЕМЕННЫЕ ПРОБЛЕМЫ
МОРСКОЙ ЛЕДОТЕХНИКИ
ЛЕКЦИЯ 2
ТЕОРЕТИЧЕСКИЕ МЕТОДЫ В МОРСКОЙ
ЛЕДОТЕХНИКЕ
К.Е. Сазонов, д.т.н.
Нижний Новгород 2015

2.

ТЕОРЕТИЧЕСКИЕ МЕТОДЫ
В морской ледотехнике теоритические методы применяются:
для изучения ледовых качеств судов
– Ледового сопротивления
– Ледовой прочности
– Ледовой управляемости
для расчета глобальной и локальной ледовой нагрузки на
морские инженерные сооружения
для расчетов параметров функционирования морских
транспортных систем, эксплуатируемых в ледовых условиях
для описания характеристик ледяного покрова
Лекция 2. Теоретические методы в морской ледотехнике
2

3.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ
Для определения показателей ледовой ходкости судов необходимо
знать величину сопротивления льда движению судна.
Невозможно определить ледовое сопротивление судна для всего
многообразия ледовых условий, поэтому эту характеристику
определяют для эталонных ледовых условий, под которыми обычно
понимают:
- сплошной ровный лед;
- мелкобитый лед, включая лед в канале за ледоколом;
- крупнобитый лед и обломки ледяных полей;
- канал, набитый тертым льдом;
- торосистые образования
Лекция 2. Теоретические методы в морской ледотехнике
3

4.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. КЛАССИФИКАЦИЯ МЕТОДОВ
Теоретические методы расчета ледового сопротивления условно
можно разделить на три группы:
- эмпирические;
- полуэмпирические;
- аналитические
Эмпирические методы
0 2
0.07 cos 0 sin 0
Формула Л.Г.Цоя
3
Pe 6
hlim
D
3
B
L
0
2
2. 6 f 5
sin
90
d
10
B
где 0 - угол наклона форштевня к конструктивной ватерлинии (КВЛ); 0 - угол наклона
носовой ветви ватерлинии к диаметральной плоскости на 0-ом теоретическом шпангоуте;
0 , 2 , 10 - углы развала шпангоутов на 0-ом, 2-ом и 10-ом теоретических шпангоутах
соответственно; L,B - длина и ширина судна по КВЛ; D - весовое водоизмещение судна,
т; Pe - суммарная тяга гребных винтов на режиме, близком к швартовному, т; f d коэффициент динамического трения корпуса о лед.
3
2
Лекция 2. Теоретические методы в морской ледотехнике
4

5. Полуэмпирические методы

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. КЛАССИФИКАЦИЯ МЕТОДОВ
Полуэмпирические методы
Все математические модели, созданные для описания ледового сопротивления судна
содержат решение трех основных задач:
описание процессов, происходящих при движении ледокола во льдах;
определение критериев разрушения ледового покрова и описание картины
его разрушения;
описание формы поверхности корпуса судна в районе его взаимодействия со
льдом.
Уточнение решения указанных задач составляет суть развития методов расчета ледового
сопротивления
RITOT k1 f Bh 0 k2 I gBh 2 0 k3 B x hvs y
1
2
RW , Формула Шиманского - Каштеляна
где f - предел прочности льда на изгиб, I - плотность льда; h - толщина,
преодолеваемого судном льда; В - ширина судна; vs - скорость движения судна; 0 , 2 коэффициенты Шиманского, характеризующие форму корпуса судна; k1 , k2 , k3 , x, y неизвестные коэффициенты, подлежащие определению на основе обработки данных
модельных и натурных экспериментов.
Лекция 2. Теоретические методы в морской ледотехнике
5

6. Полуэмпирические методы

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. КЛАССИФИКАЦИЯ МЕТОДОВ
Полуэмпирические методы
RI 0.011 f h 2 a1 B 2 f d a2 L
Формула Б.П.Ионова
tg
0
a1 sin 0 f d a2 1 cos 0
0.15 W I ghBL
tg B
0
2 L
2
B 2T
tg 0
1
0.7 I ghB 2 FrB 1
fd
W I ghBL
B
cos
B
2
T
0 2tg
0
2 L
здесь L , L - длина носового заострения и цилиндрической вставки соответственно;
V
- число Фруда, вычисленное по ширине
W , I - плотность воды и льда; FrB
gB
корпуса судна; a1 , a2 специальные функции формы корпуса судна, зависящие от
распределения углов наклона шпангоутов по длине носового заострения, определяемые
следующими выражениями:
1 n 0.57
1.6 cos i 0.11 ;
a 1
n i 0 sin i
a 2
1 n
1
,
n i 0 sin i
где n число шпангоутов в пределах носового заострения, которые используются для
определения функций формы; i - текущий номер шпангоута
Лекция 2. Теоретические методы в морской ледотехнике
6

7. Аналитические методы

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. КЛАССИФИКАЦИЯ МЕТОДОВ
Аналитические методы
Первая аналитическая формула была получена Р.И.Рунебергом
где R - упор винтов; - средний угол наклона батоксов; - угол между средним
наклонением сечений, перпендикулярных к батоксам и КВЛ; f - коэффициент трения льда.
Аналитические методы отличаются от полуэмпирических тем, что
эмпирическая информация используется в них при разработке моделей
физических явления, сопровождающих движение судна во льдах, а не
для подгонки конечного результата
Аналитические методы делятся на интегральные и дифференциальные
Лекция 2. Теоретические методы в морской ледотехнике
7

8.

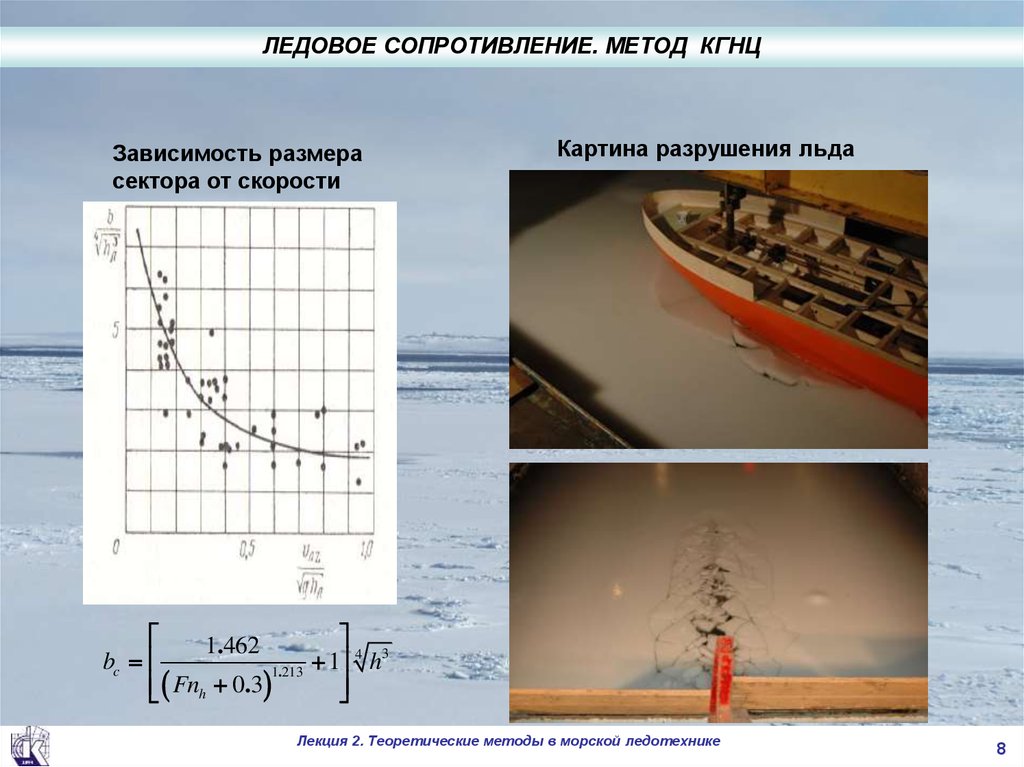
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. МЕТОД КГНЦ
Зависимость размера
сектора от скорости
Картина разрушения льда
1.462
bc
1 4 h3
1.213
Fnh 0.3
Лекция 2. Теоретические методы в морской ледотехнике
8

9.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. МЕТОД КГНЦ
Картина разрушения льда
При
построении
картины
разрушения
льда
ширина
сектора
определяется с учетом влияния на нее скорости движения ледокола,
угла наклона батокса в точке контакта корпуса со льдом, физикомеханических свойств льда и его толщины.
При определении остальных размеров секторов приняты следующие
допущения:
- концентрическая трещина, по которой образуется сектор, является
дугой некоторой окружности, центр которой не обязательно лежит в
диаметральной плоскости ледокола;
- длина сектора параллельна, а ширина сектора перпендикулярна
поверхности корпуса ледокола в районе точки контакта со льдом,
которая предполагается плоской
Лекция 2. Теоретические методы в морской ледотехнике
9

10.

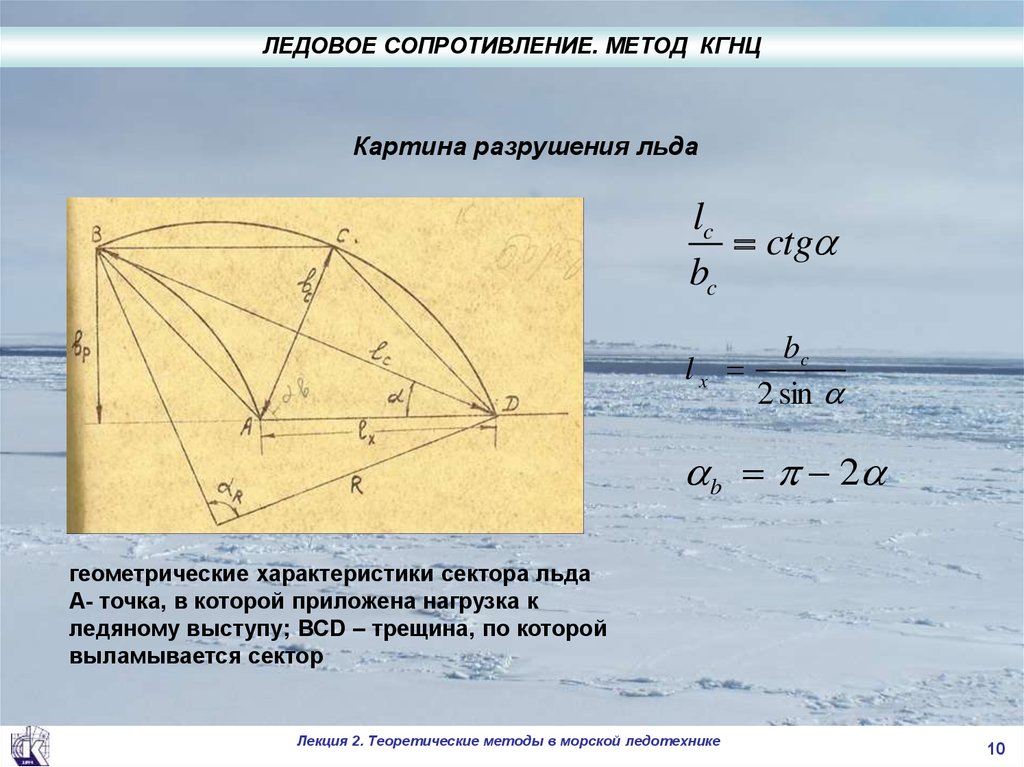
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. МЕТОД КГНЦ
Картина разрушения льда
lc
ctg
bc
lx
bc
2 sin
b 2
геометрические характеристики сектора льда
А- точка, в которой приложена нагрузка к
ледяному выступу; ВСD – трещина, по которой
выламывается сектор
Лекция 2. Теоретические методы в морской ледотехнике
10

11.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. МЕТОД КГНЦ
Алгоритм построения картины разрушения льда
y f x
x f
1
уравнение действующей ватерлинии
(y )
y h
y h b p1
координата первой точки контакта
координата следующей точки контакта
Расчет заканчивается при выполнении условия
n
h b pi
i 1
B
2
Лекция 2. Теоретические методы в морской ледотехнике
11

12.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. МЕТОД КГНЦ
Общий вид картины разрушения льда
Лекция 2. Теоретические методы в морской ледотехнике
12

13.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. МЕТОД КГНЦ
RITOT = RI + Rw =RIB + RIS + RIF + RIV + RW
где RITOT - полное ледовое сопротивление, RI - чистое ледовое сопротивление, RW сопротивление воды движению судна; RIB -сопротивление, связанное с разрушением
ледового поля; RIS - сопротивление, зависящее от поворота и притапливания обломков
разрушенного льда; RIF - сопротивление трения "ледовой рубашки" о корпус ледокола; RIV
- добавочное вязкостное сопротивление воды движению судна, возникающее из-за
влияния "ледовой рубашки" на процесс обтекания водой корпуса.
Лекция 2. Теоретические методы в морской ледотехнике
13

14.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. СОПРОТИВЛЕНИЕ ЛОМКИ ЛЬДА
M 1 k11 xg T N cos(n, x) f ID cos cos ,
M 1 k33 z g T W gS z g b N cos(n, z ) f ID cos sin ,
I 1 k55 T hS a W gS z g b b a DH
N cos(n, x) f ID cos cos fU a z g
N cos(n, z ) f ID cos sin LA xCM xg
N 2 c SCM
Pz QI
fU
z pl
I
2
1
W gD0
Лекция 2. Теоретические методы в морской ледотехнике
14

15.

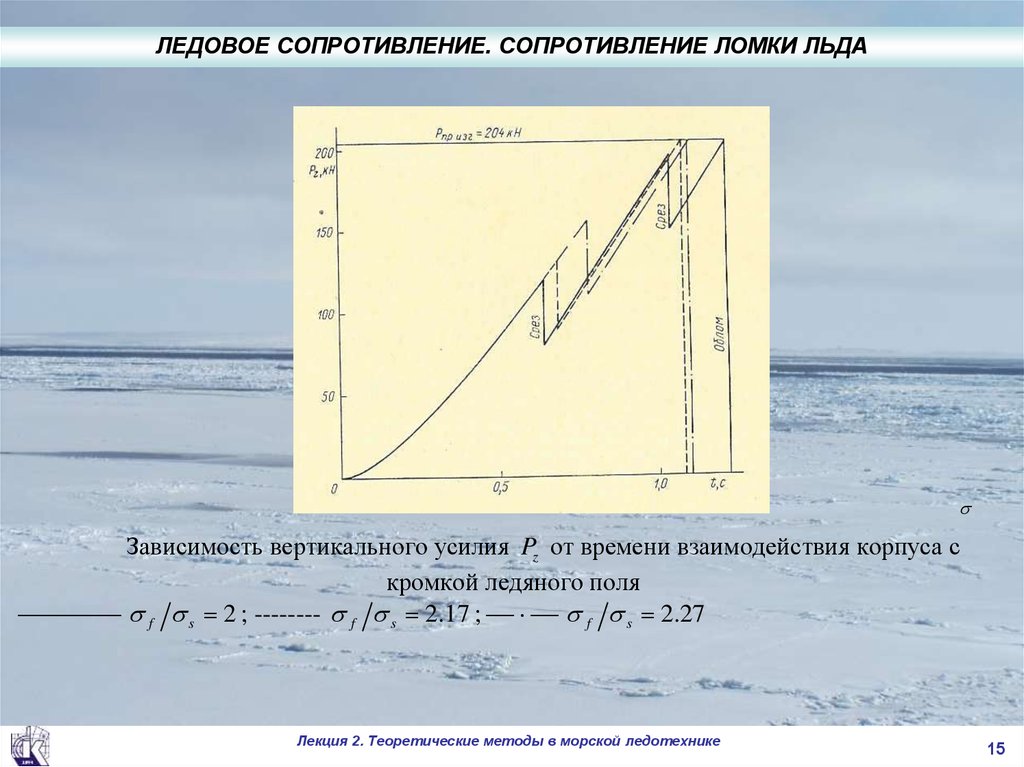
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. СОПРОТИВЛЕНИЕ ЛОМКИ ЛЬДА
Зависимость вертикального усилия Pz от времени взаимодействия корпуса с
кромкой ледяного поля
f s 2 ; -------- f s 2.17 ; f s 2.27
Лекция 2. Теоретические методы в морской ледотехнике
15

16.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. СОПРОТИВЛЕНИЕ ПОВОРОТА ЛЬДА
J M I M P M A M Q MW
где МI - момент контактных сил, действующих на сектор со стороны корпуса; МP - момент
силы веса льдины; МA - момент гидростатических сил; МQ - момент сил, действующих на
сектор со стороны подпирающих его обломков "ледовой рубашки"; МW - момент сил
сопротивления воды; J - момент инерции массы сектора относительно точки поворота с
учетом присоединенных масс; - угол поворота сектора
Зависимость величины работы от времени,
затраченной на поворот одного сектора
Лекция 2. Теоретические методы в морской ледотехнике
16

17.

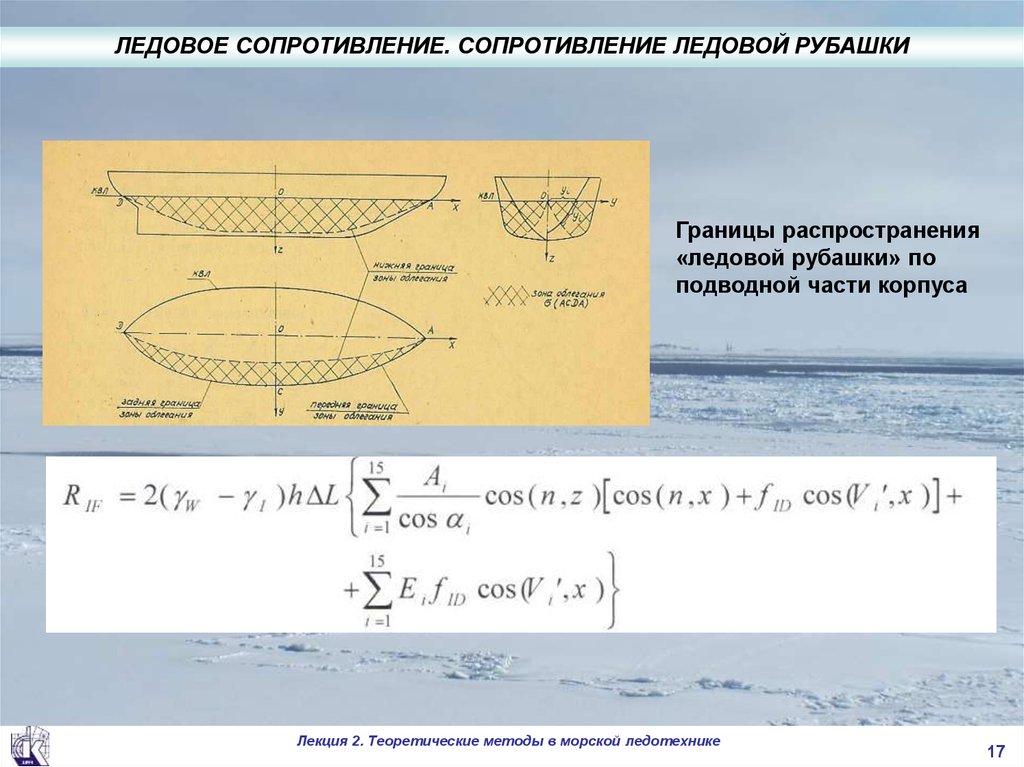
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. СОПРОТИВЛЕНИЕ ЛЕДОВОЙ РУБАШКИ
Границы распространения
«ледовой рубашки» по
подводной части корпуса
Лекция 2. Теоретические методы в морской ледотехнике
17

18.

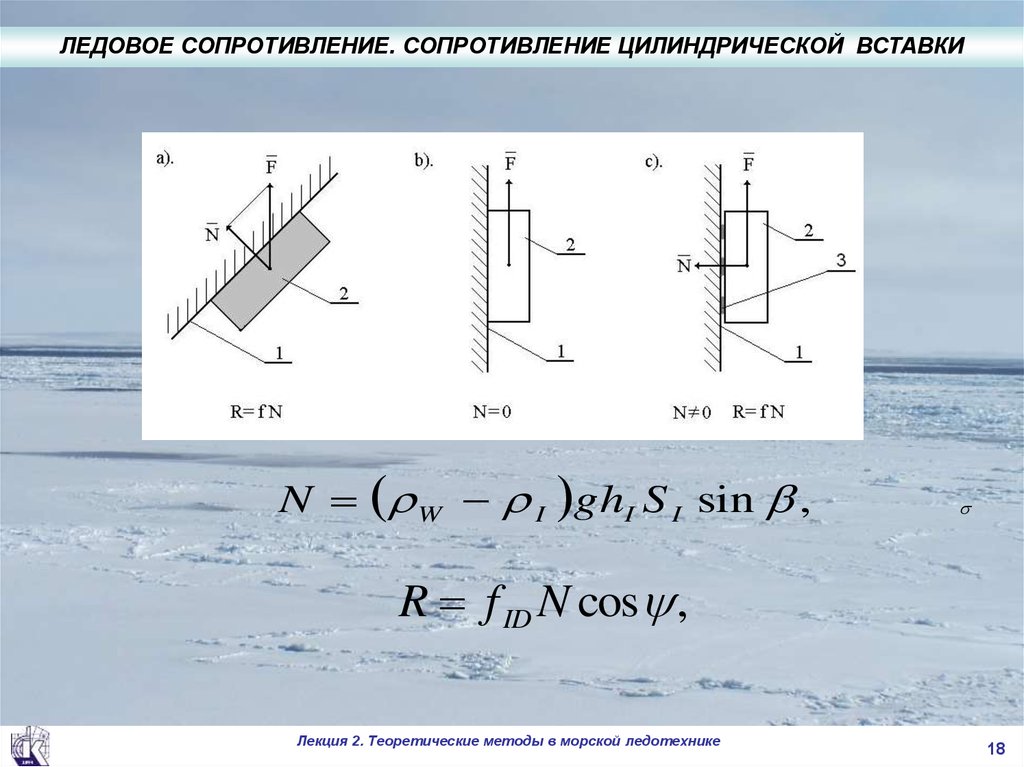
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. СОПРОТИВЛЕНИЕ ЦИЛИНДРИЧЕСКОЙ ВСТАВКИ
N W I ghI S I sin ,
R f ID N cos ,
Лекция 2. Теоретические методы в морской ледотехнике
18

19.

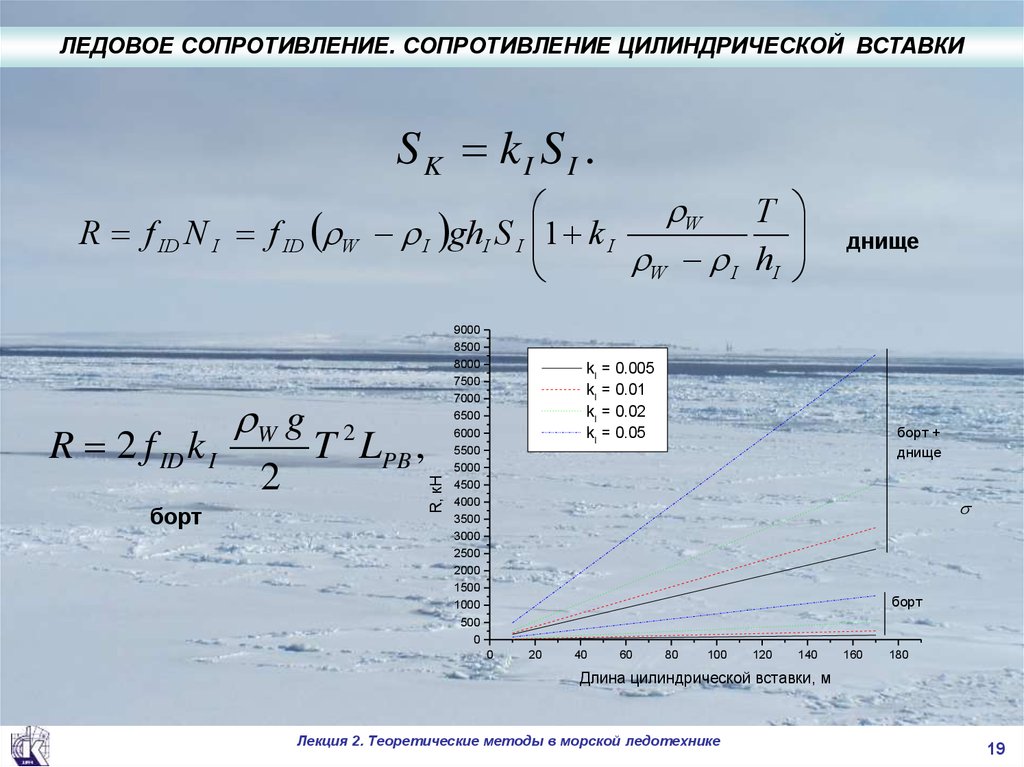
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. СОПРОТИВЛЕНИЕ ЦИЛИНДРИЧЕСКОЙ ВСТАВКИ
SK kI SI .
W
T
R f ID N I f ID W I ghI S I 1 k I
W I hI
борт
2
2
T LPB ,
R, кН
R 2 f ID k I
W g
9000
8500
8000
7500
7000
6500
6000
5500
5000
4500
4000
3500
3000
2500
2000
1500
1000
500
0
днище
kI = 0.005
kI = 0.01
kI = 0.02
kI = 0.05
борт +
днище
борт
0
20
40
60
80
100
120
140
160
180
Длина цилиндрической вставки, м
Лекция 2. Теоретические методы в морской ледотехнике
19

20.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. СОПРОТИВЛЕНИЕ ЦИЛИНДРИЧЕСКОЙ ВСТАВКИ
Подводное нагромождение льда,
формирующееся у вертикальных
бортов цилиндрической вставки
hI = 0.5 м
hI = 1.0 м
hI = 1.5 м
Сопротивление цилиндрической
вставки, кН
1400
1200
Т = 16 м
Т = 13 м
1000
Т = 16 м
Т = 10 м
800
Т = 13 м
600
Т = 10 м
Т = 16 м
Т = 13 м
Т = 13 м
400
200
Rцил 0.22hI TLцил
0
50
100
150
200
250
Длина цилиндрической вставки, м
Лекция 2. Теоретические методы в морской ледотехнике
20

21.

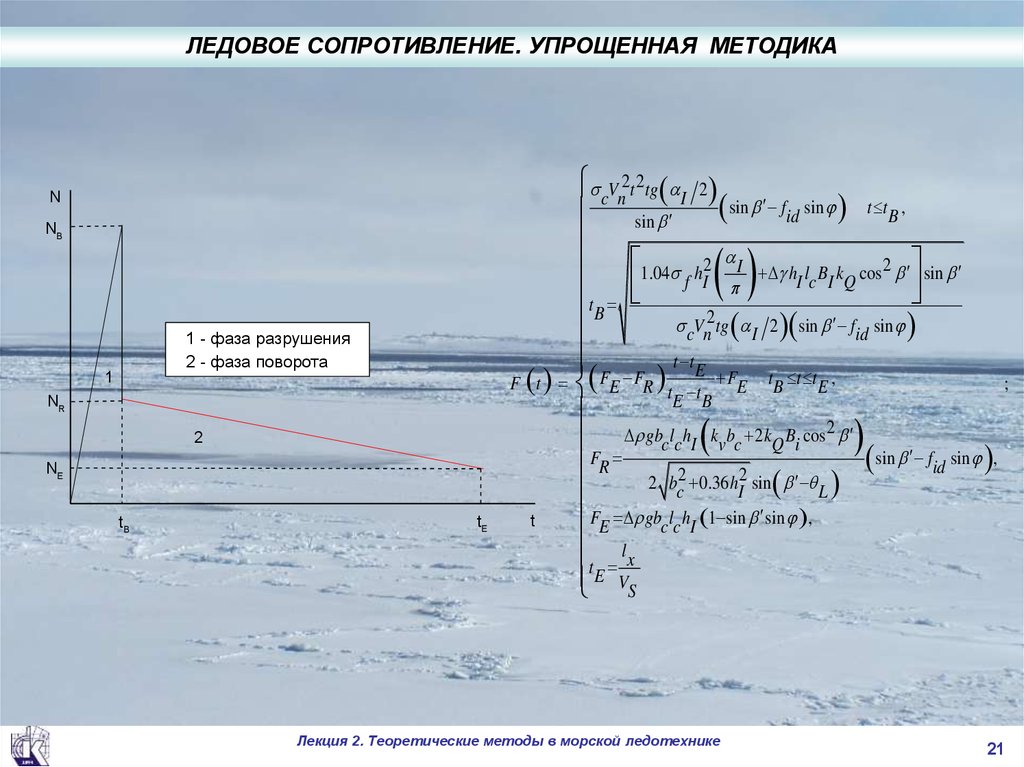
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. УПРОЩЕННАЯ МЕТОДИКА
N
NB
cVn2t 2tg I 2
sin sin fid sin t tB ,
1.04 f hI2 I hI lc BI kQ cos 2 sin
tB
2
cVn tg I 2 sin fid sin
F F t tE F t t t ,
F t E R t t
;
E B
E
E B
gb l h k b 2 k B cos2
sin f sin ,
FR c c I v c Q i
id
2 bc2 0.36 hI2 sin L
FE gbclc hI 1 sin sin ,
t
lx
tE VS
1 - фаза разрушения
2 - фаза поворота
1
NR
2
NE
tB
tE
Лекция 2. Теоретические методы в морской ледотехнике
21

22.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. АСИНХРОННОСТЬ ВЗАИМОДЕЙСТВИЯ
.
f
1
h f
Ti 1
1
n 1
h
b
p
i
i 1
;
Vs
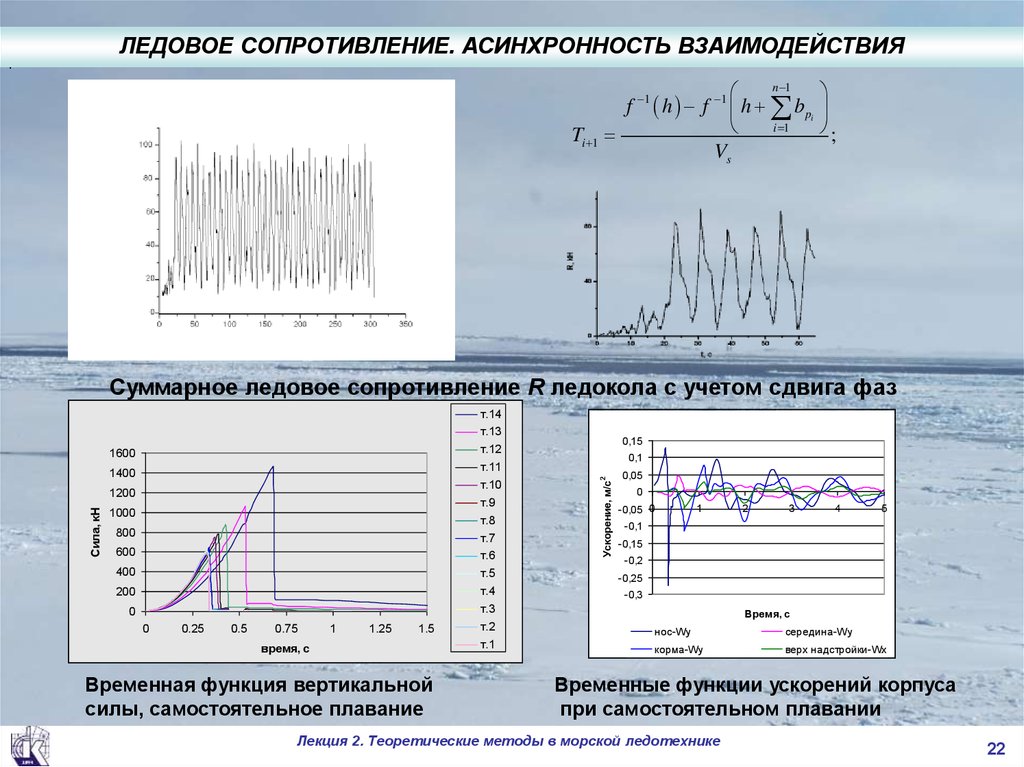
Суммарное ледовое сопротивление R ледокола с учетом сдвига фаз
т.14
Сила, кН
1200
т.11
т.10
0,05
т.9
т.8
1000
800
т.7
т.6
600
400
т.5
т.4
200
0
0
0.25
0.5
0.75
1
1.25
1.5
время, с
Временная функция вертикальной
силы, самостоятельное плавание
т.3
т.2
т.1
0,1
2
1400
0,15
Ускорение, м/c
1600
т.13
т.12
0
-0,05 0
1
2
3
4
5
-0,1
-0,15
-0,2
-0,25
-0,3
Время, с
нос-Wy
середина-Wy
корма-Wy
верх надстройки-Wx
Временные функции ускорений корпуса
при самостоятельном плавании
Лекция 2. Теоретические методы в морской ледотехнике
22

23.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. МЕЛКОБИТЫЙ ЛЕД
.
Формула А.Я.Рывлина
L
B
R I 10 I rhI k1 1 2 f ID B k 2 I rhI B f ID B tg 0 Fn
B
2
2
k 3 I rhI Ltg 2 0 Fn 2
k1 3 2s 0.25s 2 10 2 ; 6 s 10;
k1 0; s 6;
k2 0.46 0.305s 0.1125s .
2
rh 0.0114 0.4543hI 0.5429h
2
I
B
L
,
2tg
L* L L
Лекция 2. Теоретические методы в морской ледотехнике
23

24.

ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. КРУПНОБИТЫЙ ЛЕД
.
RI C 9v1.3 hI1.2
x
b
x
v
(1 k ) M I x F PW PI
t*
RIc
1
R x t dt
* Ic
t 0
*
vt
RI*
RIc
b
Лекция 2. Теоретические методы в морской ледотехнике
24

25.

.
ЛЕДОВОЕ СОПРОТИВЛЕНИЕ. НАБИТЫЕ КАНАЛЫ
R ch C1 H F H M
2 B 1.85H F
2H F
tg
0.15 cos 2 sin sin
3
LT
C 2 L PM H F2 C 3 2 H M A wf Fn 2 ,
B
где 2 – угол наклона батокса в точке, в которой ширина корпуса равна В/4; Awf –
площадь носовой ветви ватерлинии; НМ – толщина набитого льда в канале; HF – увеличение
толщины набитого льда при движении судна H F 0.26 H M B ; С1=0,85 кН/м3; С2=0,04
кН/м3; С3=1,2 кН/м3.
Лекция 2. Теоретические методы в морской ледотехнике
25

26.

ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ОСНОВНЫЕ МАНЕВРЫ
.
Циркуляция
Выход из канала
Разворот методом «елочка»
Выход кормой из канала
Лекция 2. Теоретические методы в морской ледотехнике
26

27.

.
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ДВИЖЕНИЕ С УГЛОМ ДРЕЙФА
b ;
s ;
tg
b arctg
;
(1 tg tg ) cos
cos tg
s arctg
;
1 sin tg
b [ x ytg ] cos ;
s [ y xtg ]sin x / cos ;
b [ x ytg ]sin y / cos ;
s [ y xtg ] cos ;
Лекция 2. Теоретические методы в морской ледотехнике
27

28.

.
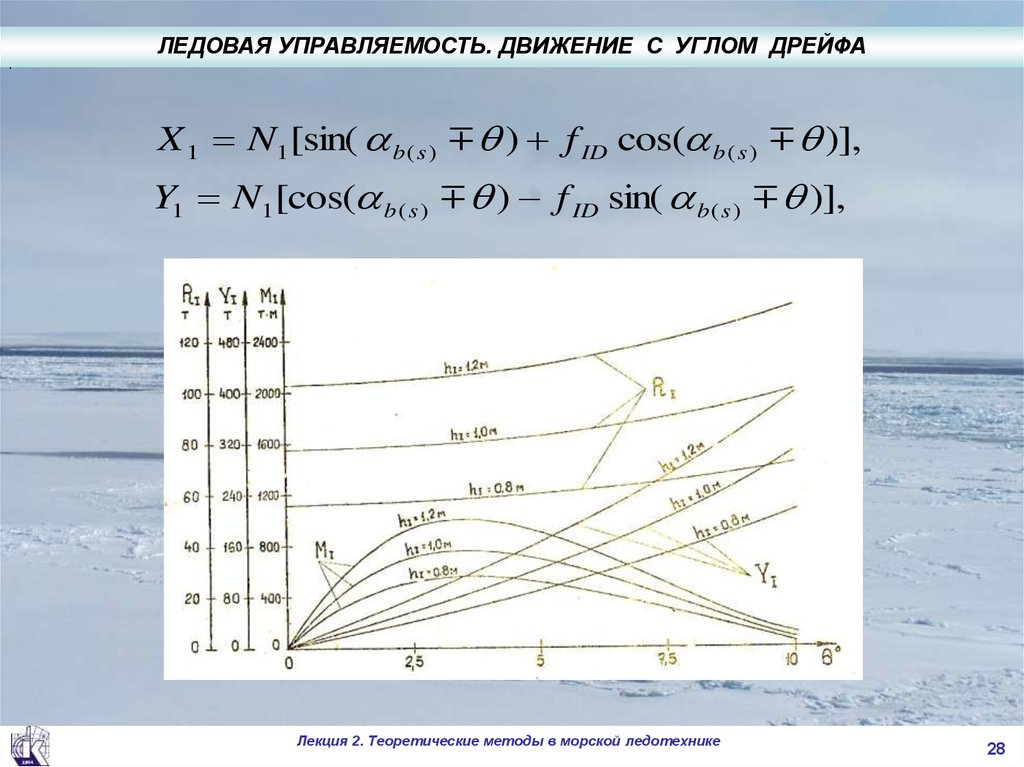
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ДВИЖЕНИЕ С УГЛОМ ДРЕЙФА
X 1 N1[sin( b ( s ) ) f ID cos( b ( s ) )],
Y1 N1[cos( b ( s ) ) f ID sin( b ( s ) )],
Лекция 2. Теоретические методы в морской ледотехнике
28

29.

.
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. МЕТОД РАСЧЕТА
k V
V ex V sin( ) r sign cos( ) q k B
I
s ef
d n
n
s
V in V sin( ) rcos( )
y
L
n
s
Bef
x y tg 1 sin 1 ,
cos 1
2
VS sin r cos
1
VS cos r sin
Лекция 2. Теоретические методы в морской ледотехнике
29

30.

.
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ОПРЕДЕЛЕНИЕ СИЛ
L/2
F (k B k V ex sin )(cos sin f cos cos )dx
X
s ef
d n
Id
x1
R R
AV
I
ST
S
R
IS
k
,
s
L/2
2 y ( x)(cos sin f cos cos )dx
Id
0
A
k
d
L/2
2 sin (cos sin f cos cos )dx
Id
0
L/2
(k B k V in sin )(cos sin f cos cos )dx
s ef
d n
Id
x2
L/2
F (k B k V ex sin )(cos cos f cos sin )dx
Y
s ef
d n
Id
x1
L/2
in
(k s Bef k d Vn sin )(cos cos f Id cos sin )dx
x2
L/2
M (k B k V ex sin )(cos cos f cos sin ) xdx
s ef
d n
Id
x1
L/2
ex
(k s Bef k d Vn sin )(cos sin f Id cos cos ) y dx
x1
L/2
in
(k s Bef k d Vn sin )(cos cos f Id cos sin ) xdx
x2
L/2
in
(k s Bef k d Vn sin )(cos sin f Id cos cos ) y dx
x2
Лекция 2. Теоретические методы в морской ледотехнике
30

31.

ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ДВИЖЕНИЕ НА ЦИРКУЛЯЦИИ
.
руль
ВРК
X X I X R TE 0;
X X I TE cos 0;
Y YI TE sin 0;
Y YI YR 0;
M M I TE sin l AP 0.
M M I M R 0.
V 1 k 22 v S C X 0
2
v S2 AL
C XR v S2 ARE TE
XI
0;
2
T cos
0
E
V 1 k11 v S С c2
C M
2
Y
v AL L C M
2
S
2 v
2
S
AL
YR
YI
0;
TE sin
YR l R
vS AL L M I
0
2
TE sin l AP
2
Лекция 2. Теоретические методы в морской ледотехнике
31

32.

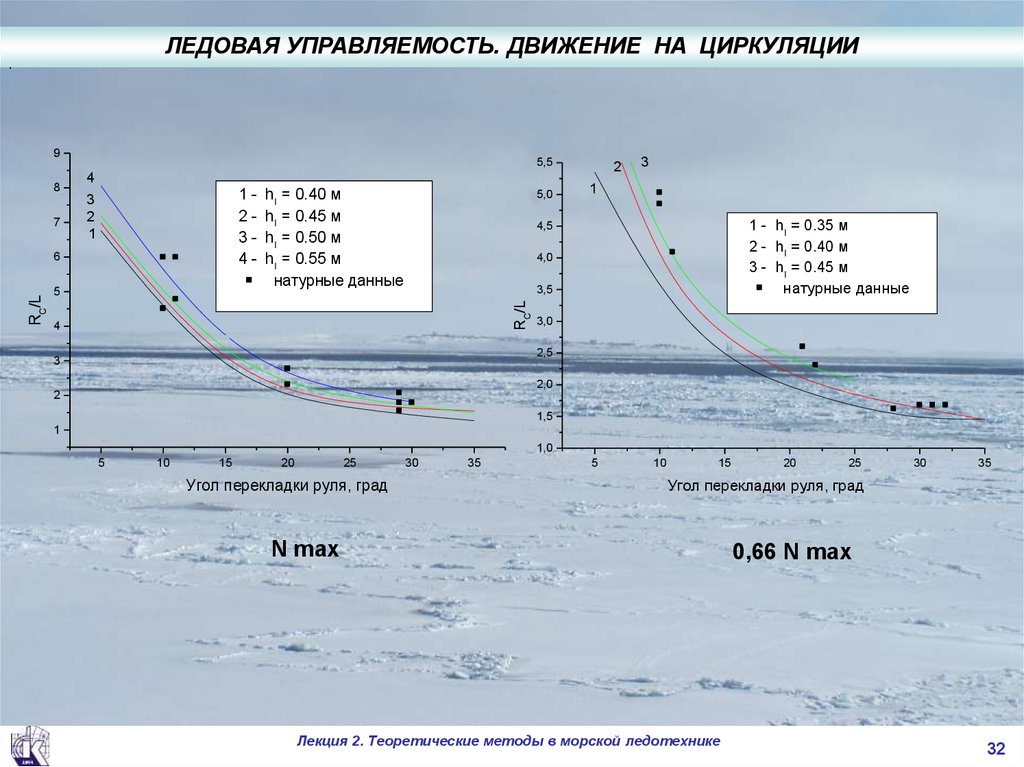
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ДВИЖЕНИЕ НА ЦИРКУЛЯЦИИ
.
9
8
7
5,5
4
1234-
3
2
1
5
5,0
3
1
1 - hI = 0.35 м
2 - hI = 0.40 м
3 - hI = 0.45 м
натурные данные
4,5
4,0
3,5
RC/L
RC/L
6
hI = 0.40 м
hI = 0.45 м
hI = 0.50 м
hI = 0.55 м
натурные данные
2
4
3,0
2,5
3
2,0
2
1,5
1
1,0
5
10
15
20
25
Угол перекладки руля, град
30
35
5
10
15
20
25
30
35
Угол перекладки руля, град
N max
Лекция 2. Теоретические методы в морской ледотехнике
0,66 N max
32

33.

.
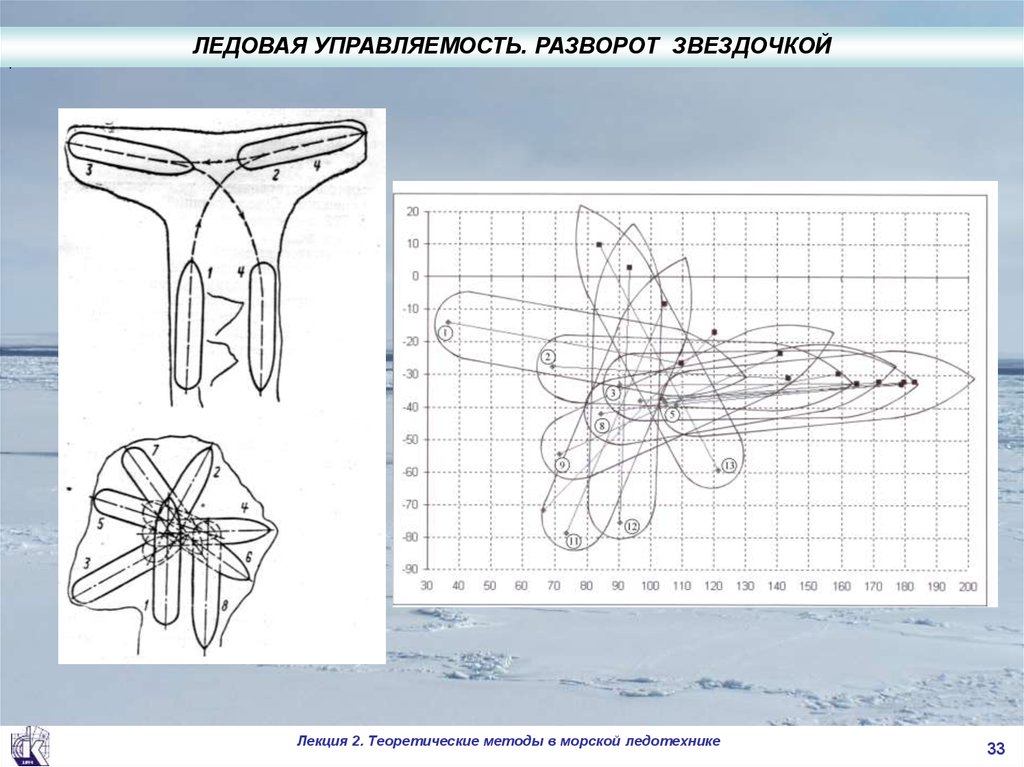
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. РАЗВОРОТ ЗВЕЗДОЧКОЙ
Лекция 2. Теоретические методы в морской ледотехнике
33

34.

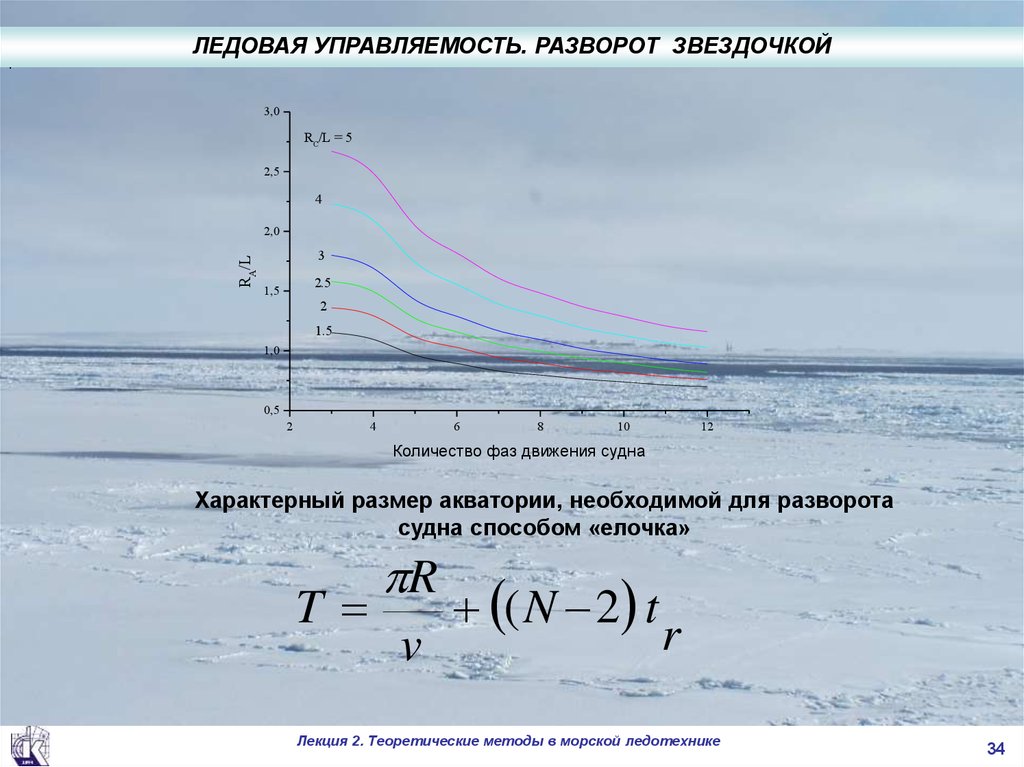
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. РАЗВОРОТ ЗВЕЗДОЧКОЙ
3,0
RC/L = 5
2,5
4
2,0
RA/L
.
3
2.5
1,5
2
1.5
1,0
0,5
2
4
6
8
10
12
Количество фаз движения судна
Характерный размер акватории, необходимой для разворота
судна способом «елочка»
T
R
v
( N 2 t
r
Лекция 2. Теоретические методы в морской ледотехнике
34

35.

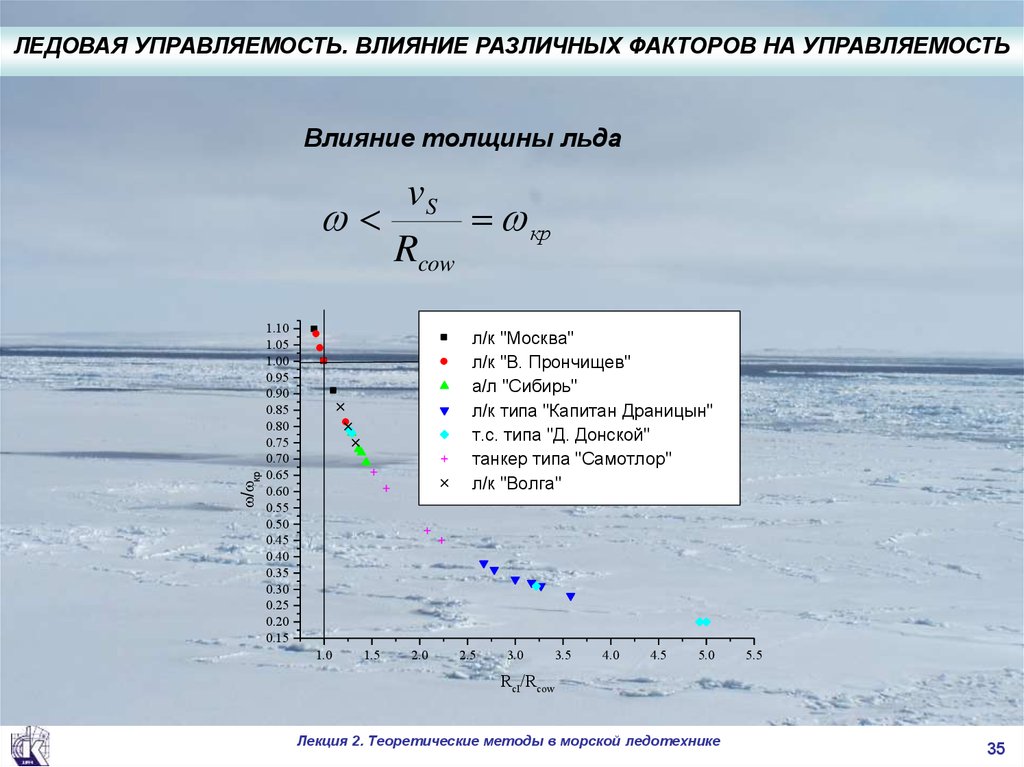
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ВЛИЯНИЕ РАЗЛИЧНЫХ ФАКТОРОВ НА УПРАВЛЯЕМОСТЬ
Влияние толщины льда
vS
кр
Rcow
/ кр
.
1.10
1.05
1.00
0.95
0.90
0.85
0.80
0.75
0.70
0.65
0.60
0.55
0.50
0.45
0.40
0.35
0.30
0.25
0.20
0.15
л/к "Москва"
л/к "В. Прончищев"
а/л "Сибирь"
л/к типа "Капитан Драницын"
т.с. типа "Д. Донской"
танкер типа "Самотлор"
л/к "Волга"
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
RcI/Rcow
Лекция 2. Теоретические методы в морской ледотехнике
35

36.

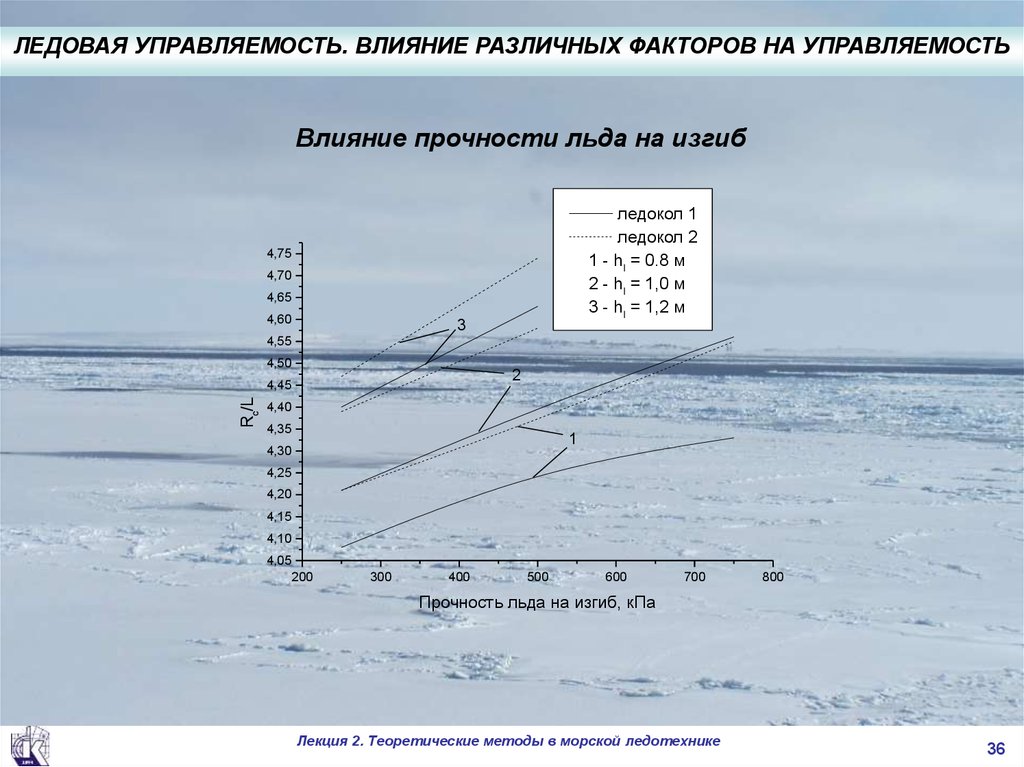
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ВЛИЯНИЕ РАЗЛИЧНЫХ ФАКТОРОВ НА УПРАВЛЯЕМОСТЬ
Влияние прочности льда на изгиб
ледокол 1
ледокол 2
1 - hI = 0.8 м
2 - hI = 1,0 м
3 - hI = 1,2 м
4,75
4,70
4,65
4,60
3
4,55
4,50
2
4,45
Rc/L
.
4,40
4,35
1
4,30
4,25
4,20
4,15
4,10
4,05
200
300
400
500
600
700
800
Прочность льда на изгиб, кПа
Лекция 2. Теоретические методы в морской ледотехнике
36

37.

.
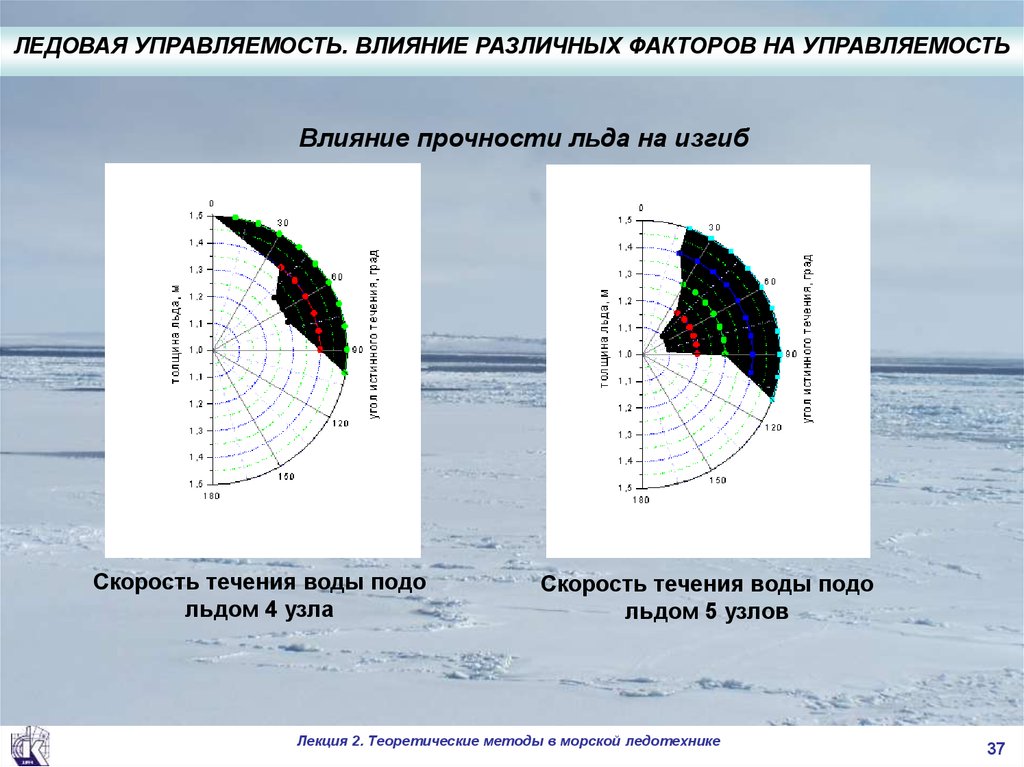
ЛЕДОВАЯ УПРАВЛЯЕМОСТЬ. ВЛИЯНИЕ РАЗЛИЧНЫХ ФАКТОРОВ НА УПРАВЛЯЕМОСТЬ
Влияние прочности льда на изгиб
Скорость течения воды подо
льдом 4 узла
Скорость течения воды подо
льдом 5 узлов
Лекция 2. Теоретические методы в морской ледотехнике
37

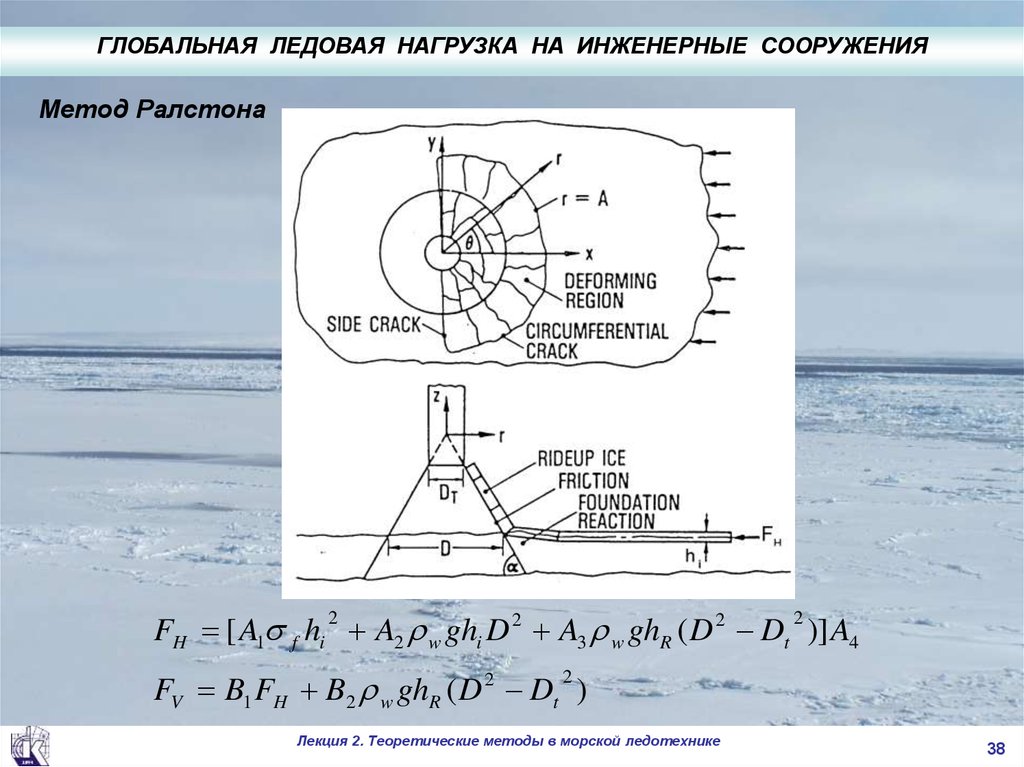
38. Метод Ралстона

.
ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Метод Ралстона
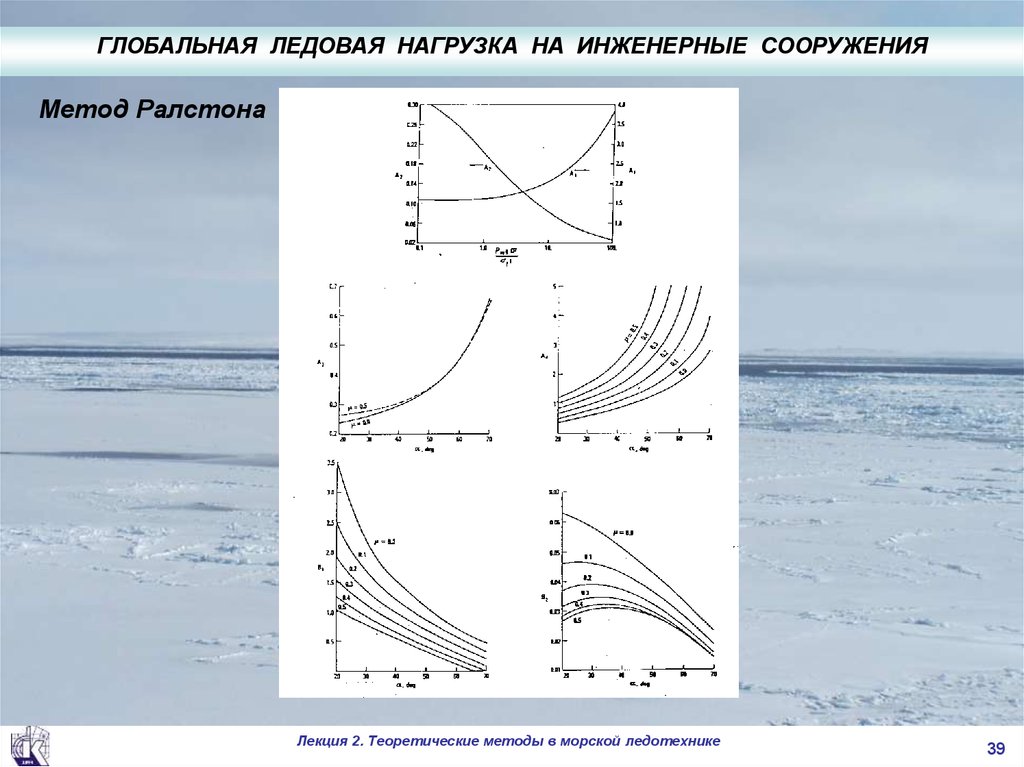
FH [ A1 f hi A2 w ghi D 2 A3 w ghR ( D 2 Dt )] A4
2
2
FV B1 FH B2 w ghR ( D 2 Dt )
2
Лекция 2. Теоретические методы в морской ледотехнике
38

39. Метод Ралстона

.
ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Метод Ралстона
Лекция 2. Теоретические методы в морской ледотехнике
39

40. Метод Кросдайла

.
ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Метод Кросдайла
Лекция 2. Теоретические методы в морской ледотехнике
40

41. Метод Кросдайла

.
ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Метод Кросдайла
H total H b H p H r H l H t
H b 0.68 f ( w gh / E )
5
1/ 4
sin cos
(
)[ D ( 2 / 4)l c ] / D
cos sin
сила, необходимая для ломки ледяного поля изгибом
H p Dhr2 i i g (1 )(1 tan / tan ) 2 (1/ 2 tan )
сила, необходимая для проталкивания ледяного
поля под нагромождением
Лекция 2. Теоретические методы в морской ледотехнике
41

42. Метод Кросдайла

.
ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Метод Кросдайла
Hr
DP
(cos s sin )
сила, необходимая для проталкивания
обломков льда по наклонной поверхности
под нагромождением
P 0.5 i ( i s ) i g (1 )hr2 sin (1 / tan 1 / tan )(1 tan / tan )
0.5( i s ) i g (1 )hr2 cos (1 / tan )(1 tan / tan )
hi hr i g[(sin s cos ) / sin )
Лекция 2. Теоретические методы в морской ледотехнике
42

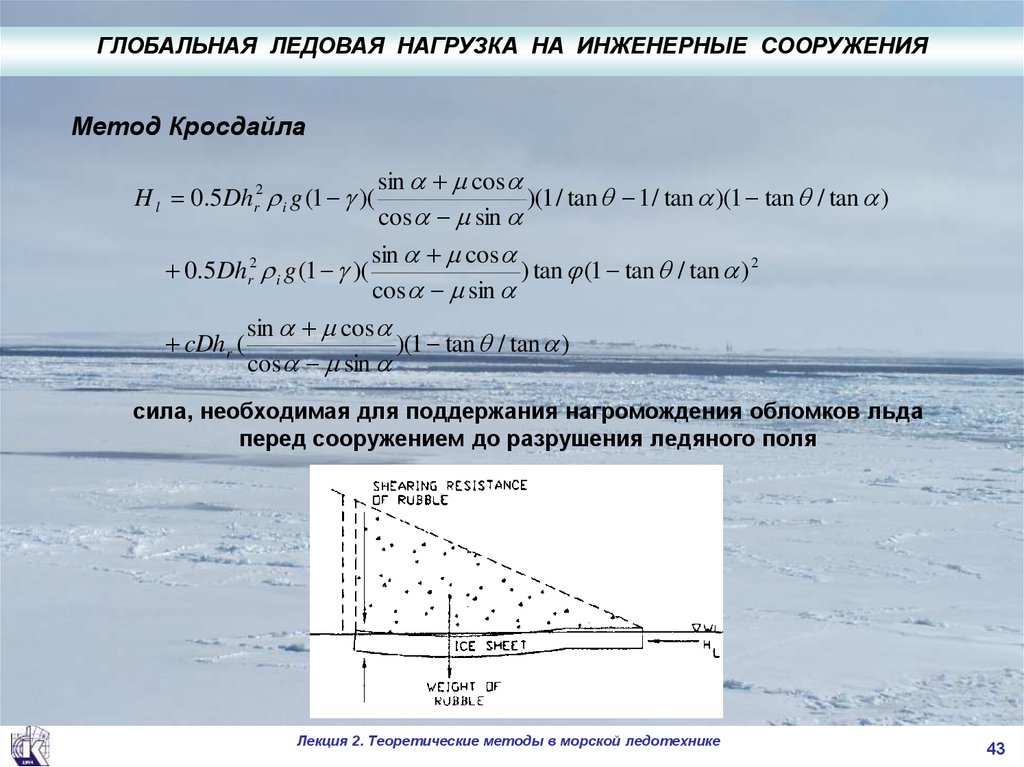
43. Метод Кросдайла

.
ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Метод Кросдайла
sin cos
)(1 / tan 1 / tan )(1 tan / tan )
cos sin
sin cos
0.5 Dhr2 i g (1 )(
) tan (1 tan / tan ) 2
cos sin
sin cos
cDhr (
)(1 tan / tan )
cos sin
H l 0.5 Dhr2 i g (1 )(
сила, необходимая для поддержания нагромождения обломков льда
перед сооружением до разрушения ледяного поля
Лекция 2. Теоретические методы в морской ледотехнике
43

44. Метод Кросдайла

.
ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Метод Кросдайла
H t 1.5Dhi2 i g[cos /(sin s cos )]
сила, необходимая для разворота блоков
льда при переходе наклонной
поверхности сооружения в вертикальную
Лекция 2. Теоретические методы в морской ледотехнике
44

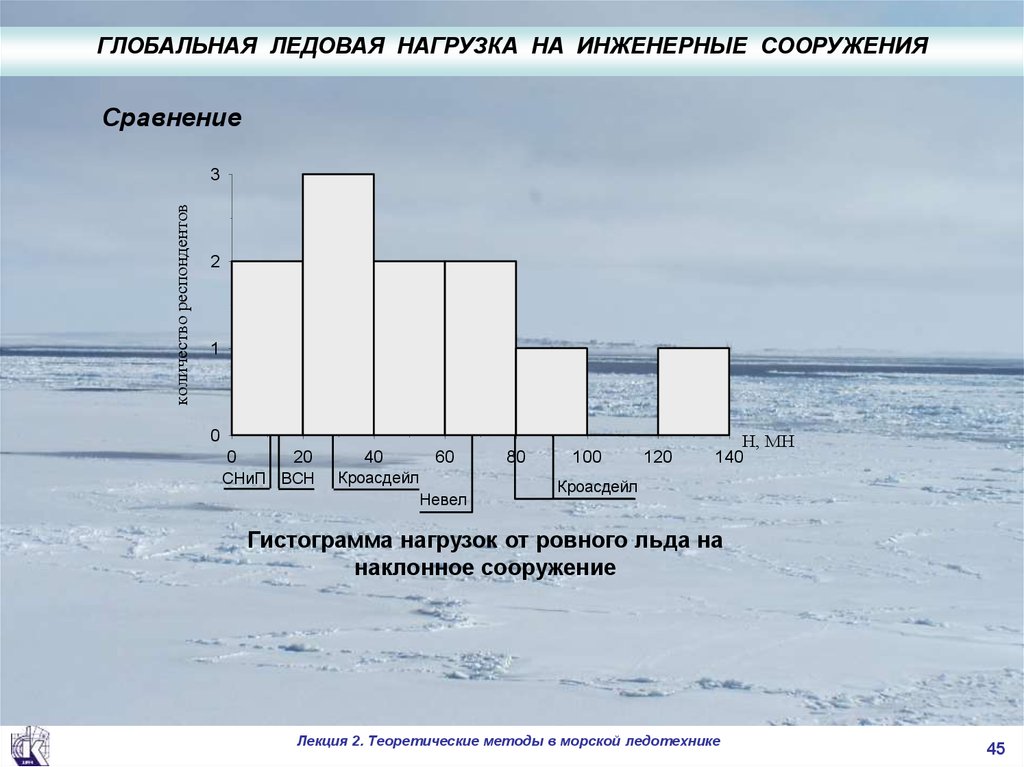
45.

ГЛОБАЛЬНАЯ ЛЕДОВАЯ НАГРУЗКА НА ИНЖЕНЕРНЫЕ СООРУЖЕНИЯ
Сравнение
3
количество респондентов
.
2
1
0
0
20
СНиП ВСН
40
60
Кроасдейл
Невел
80
100
120
H, МН
140
Кроасдейл
Гистограмма нагрузок от ровного льда на
наклонное сооружение
Лекция 2. Теоретические методы в морской ледотехнике
45

46.

Спасибо за внимание!