Начертательная геометрия. Способы преобразования проекций. (Лекция 3)

1. Начертательная геометрия

ЛЕКЦИЯ №3

2.

Способы преобразования
проекций

3.

Положение Способы преобразования проекций
применяют для получения нового изображения объекта или
группы объектов, которое позволяет упростить решение
поставленной задачи.
Как правило, это переход от общего положения к частному.

4.

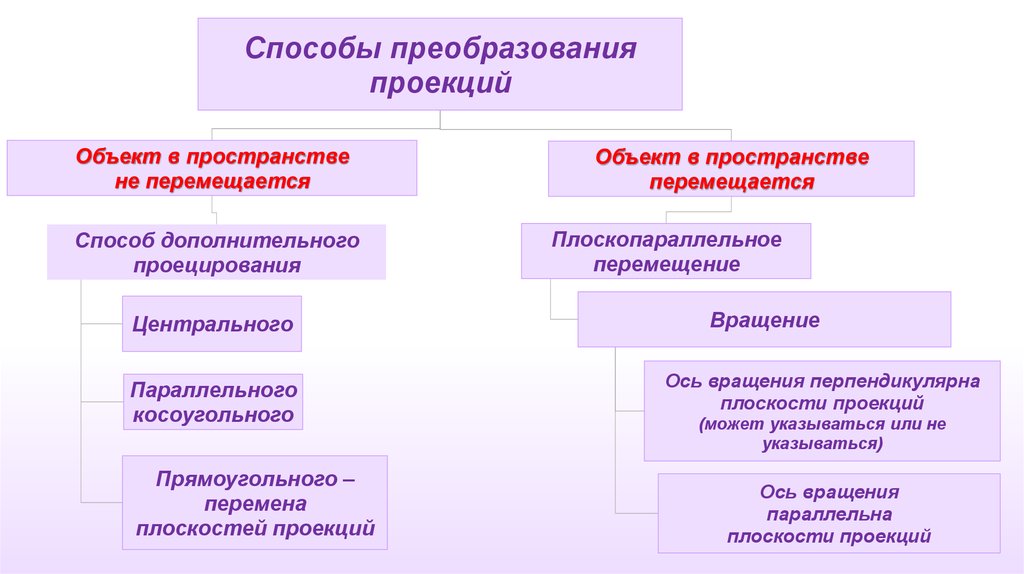
Способы преобразования
проекций
Объект в пространстве
не перемещается
Способ дополнительного
проецирования
Центрального
Параллельного
косоугольного
Прямоугольного –
перемена
плоскостей проекций
Объект в пространстве
перемещается
Плоскопараллельное
перемещение
Вращение
Ось вращения перпендикулярна
плоскости проекций
(может указываться или не
указываться)
Ось вращения
параллельна
плоскости проекций

5.

Дополнительное прямоугольное
проецирование –
перемена плоскостей проекций

6.

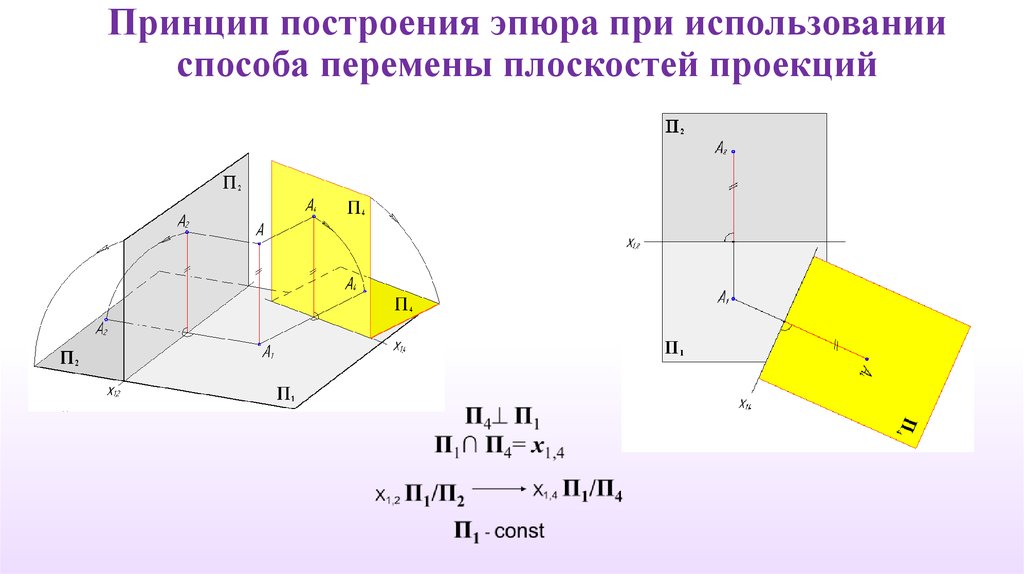
Положение Вновь вводимая плоскость проекций должна быть перпендикулярна
имеющейся.
Тем самым создаётся новая прямоугольная система плоскостей проекций.
П4 П1
П1∩ П4= х14

7.

Положение Расстояние от новой проекции точки до новой оси должно равняться
расстоянию от заменяемой проекции точки до заменяемой оси.
(А,П1) = const (А,А1) = (А2,х1,2) = (А4,х1,4).

8.

Принцип построения эпюра при использовании
способа перемены плоскостей проекций

9.

Вращение

10.

Положение Каждая точка объекта вращается вокруг
выбранной оси, перемещаясь по окружности, лежащей в
плоскости перпендикулярной оси вращения.
Положение Осью вращения может быть только прямая
частного положения – прямой уровня или проецирующей
прямой.

11.

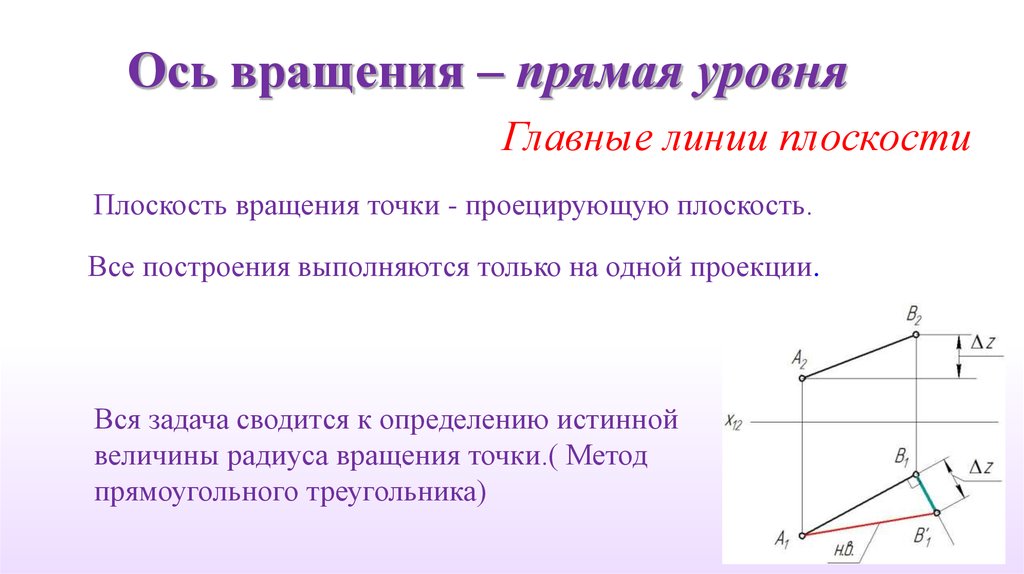
Ось вращения – прямая уровня
Главные линии плоскости
Плоскость вращения точки - проецирующую плоскость.
Все построения выполняются только на одной проекции.
Вся задача сводится к определению истинной
величины радиуса вращения точки.( Метод
прямоугольного треугольника)

12.

Ось вращения i
является
горизонталью

13.

14.

Базовые преобразования
проекций
Поскольку вновь вводимая плоскость проекций должна быть перпендикулярна
имеющейся, преобразования проводят последовательно.

15.

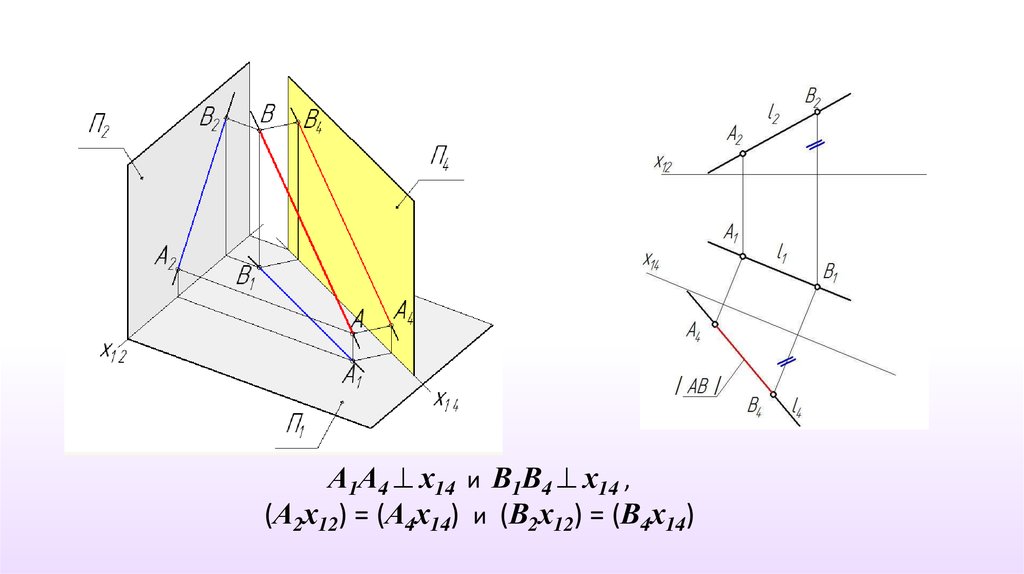
Первая задача: Заменить плоскость проекций так, чтобы
прямая общего положения стала прямой уровня.
(П2 П1)
l (AB) - прямая общего положения

16.

Вводим плоскость П4 П1 , следовательно, х14 || l1

17.

А1А4 х14 и В1В4 х14 ,
(А2х12) = (А4х14) и (В2х12) = (В4х14)

18.

Вторая задача: Заменить плоскость проекций так, чтобы прямая уровня стала проецирующей прямой.
Вводим плоскость П4 П1 , следовательно, х14 l1

19.

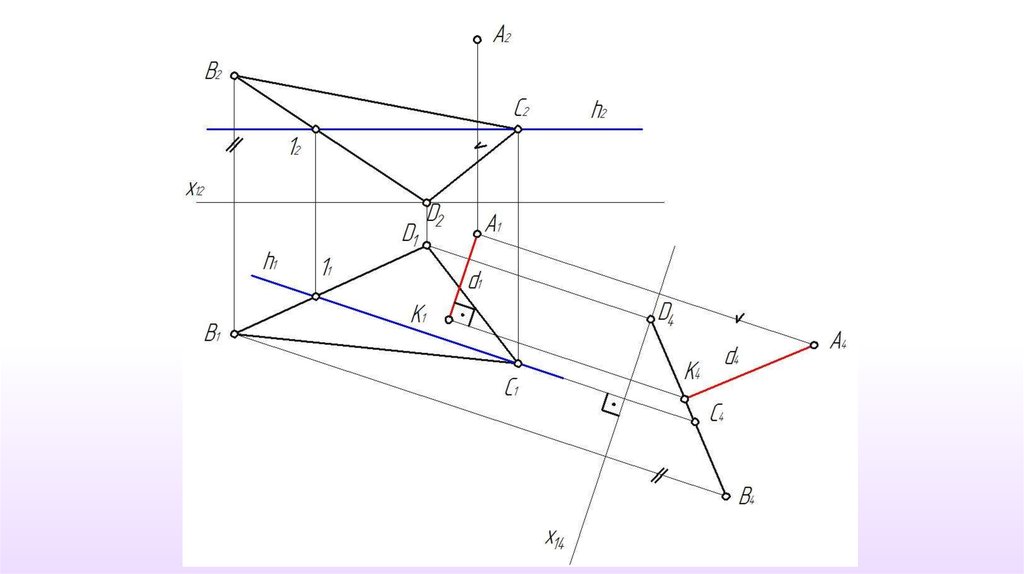
Третья задача: Заменить плоскость проекций так, чтобы плоскость общего положения
стала проецирующей плоскостью.
• Плоскость является проецирующей, если она
перпендикулярна плоскости проекций.
• Следовательно, подбираемая новая плоскость
проекций П4 должна быть перпендикулярна
заданной плоскости.
(П4 ΔABC)

20.

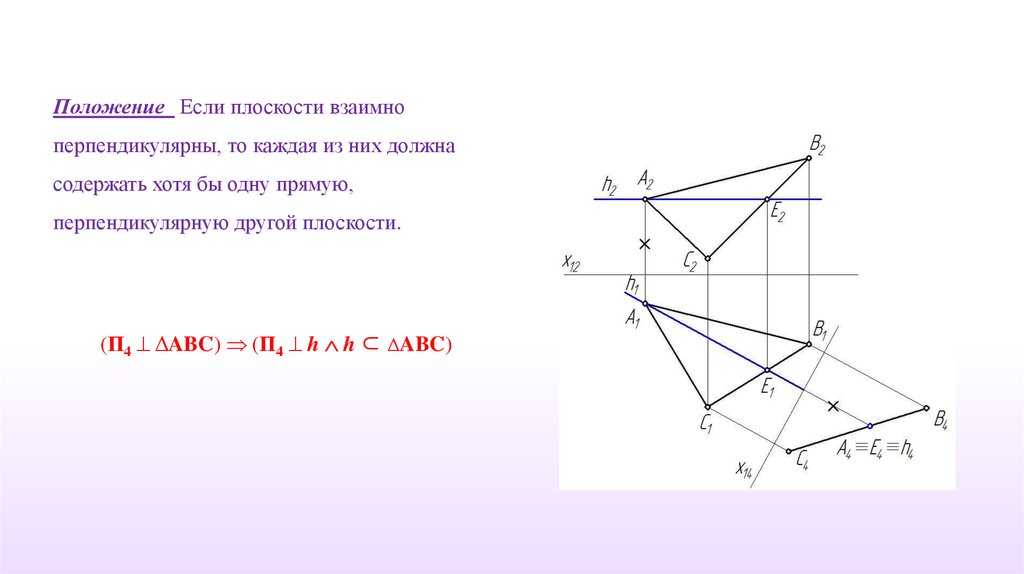
Положение Если плоскости взаимно
перпендикулярны, то каждая из них должна
содержать хотя бы одну прямую,
перпендикулярную другой плоскости.
(П4 ΔABC) (П4 h h ⊂ ΔABC)

21.

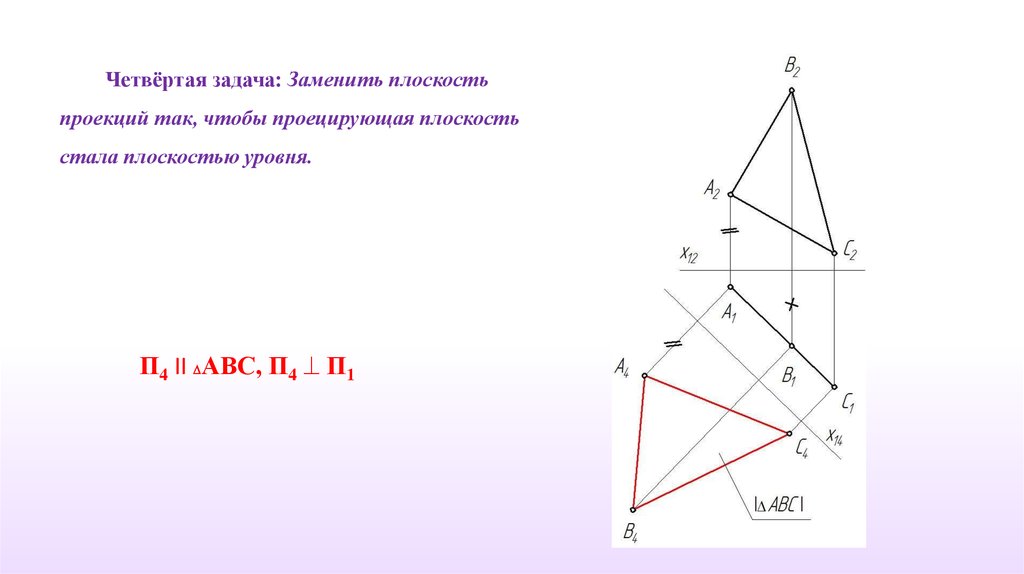
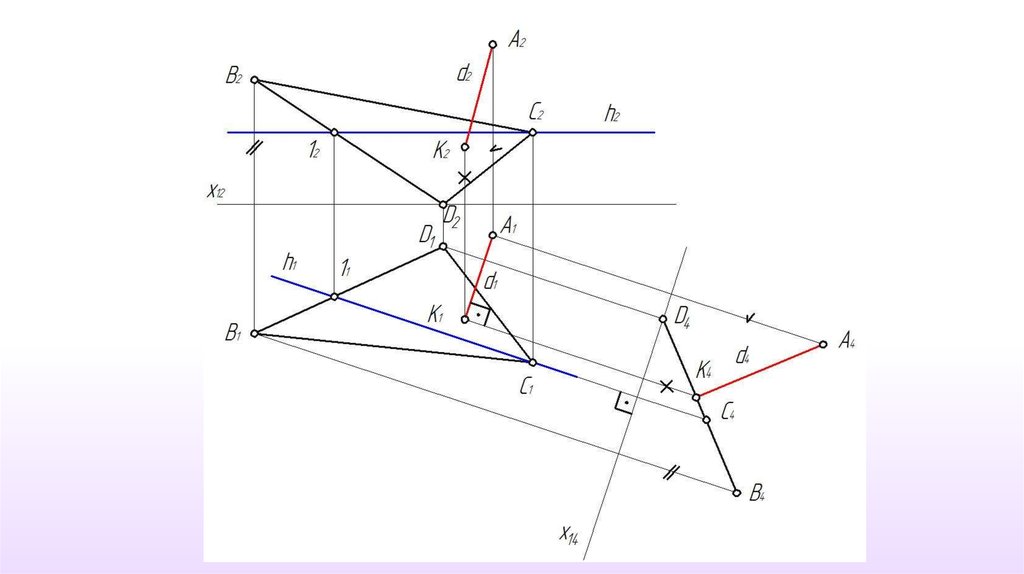
Четвёртая задача: Заменить плоскость
проекций так, чтобы проецирующая плоскость
стала плоскостью уровня.
П4 II АВС, П4 П1

22.

Построение проекции плоской фигуры на
параллельной ей плоскости проекций

23.

Решение задачи способом
замены плоскостей проекций
П′ II АВС
Так как плоскость АВС – плоскость общего положения, то и любая
плоскость ей параллельная, в том числе и проекций П′, также будет
плоскостью общего положения, что противоречит способу замены
плоскостей проекций.
Следовательно,
задача должна решаться в два этапа.

24.

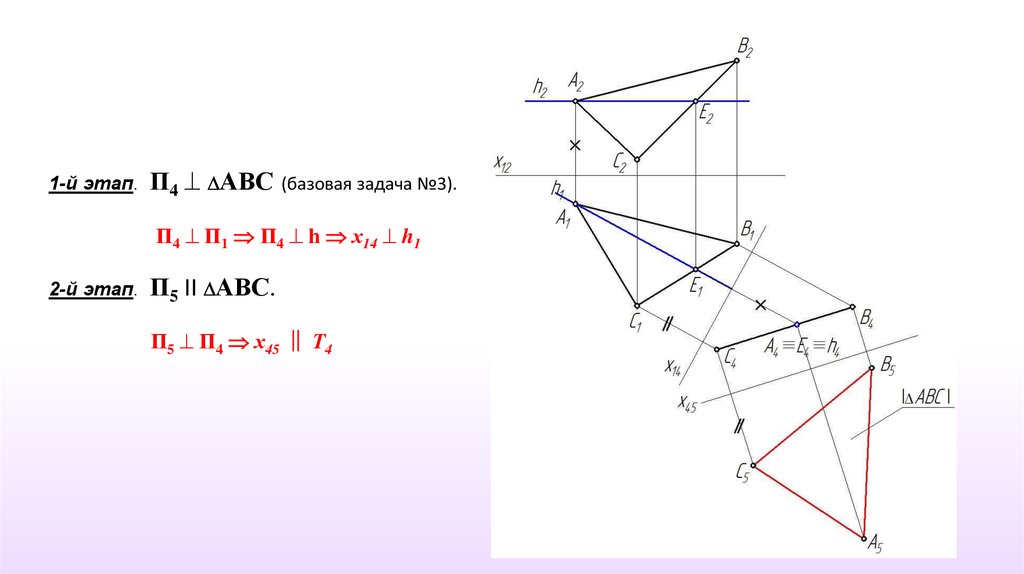
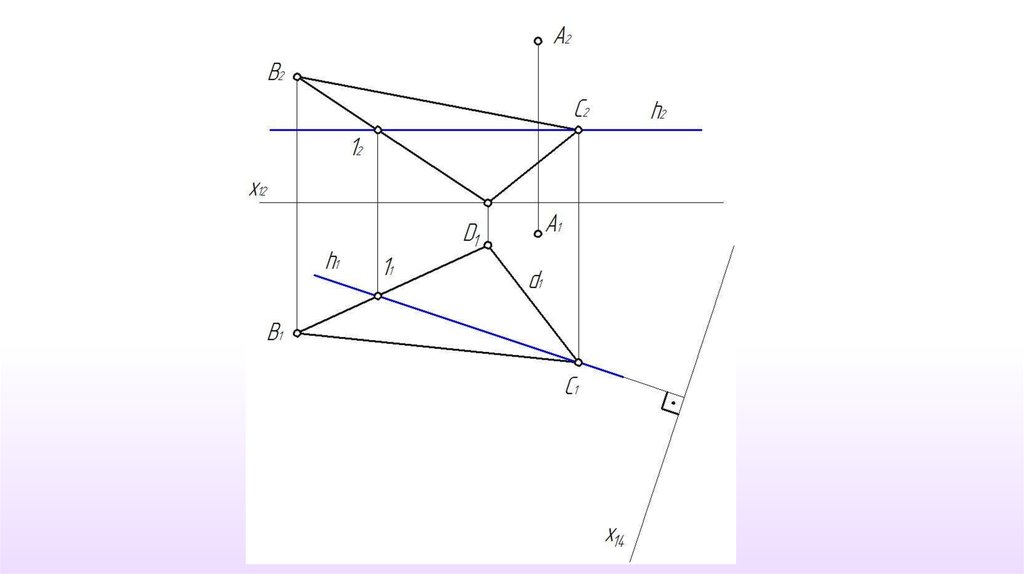
1-й этап.
П4 АВС (базовая задача №3).
П4 П1 П4 h х14 h1
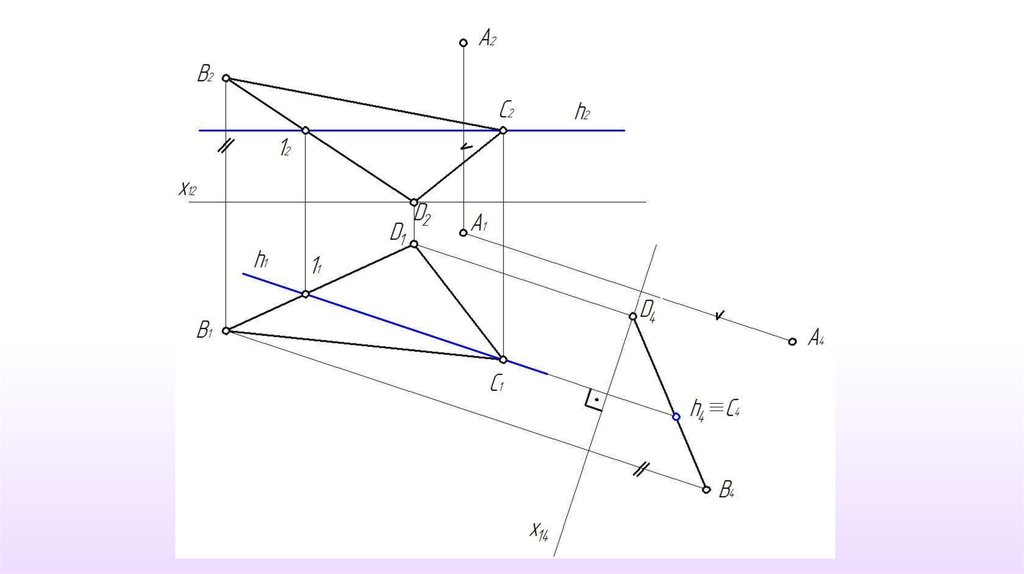
2-й этап.
П5 II АВС.
П5 П4 х45 ‖ Т4

25.

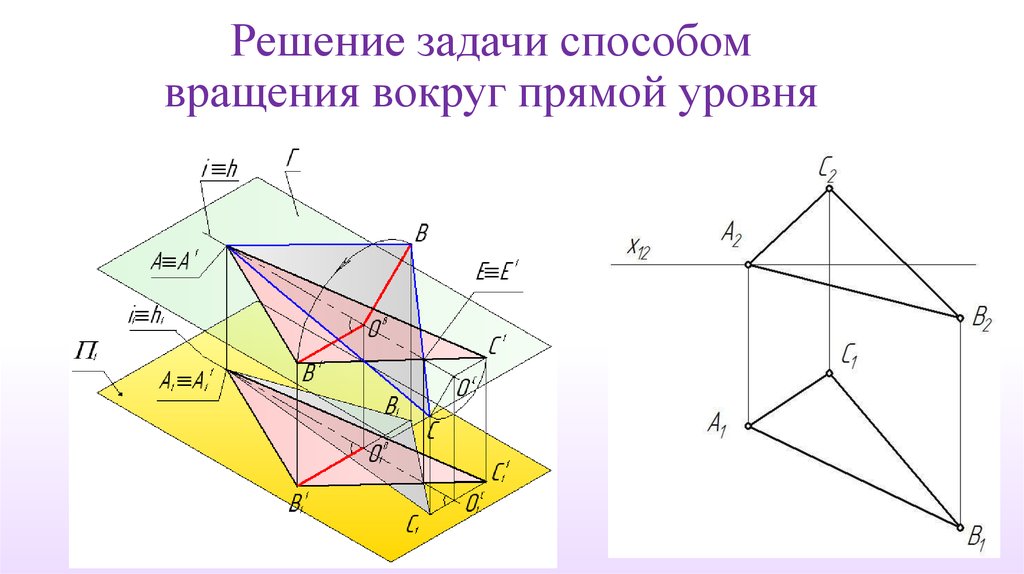
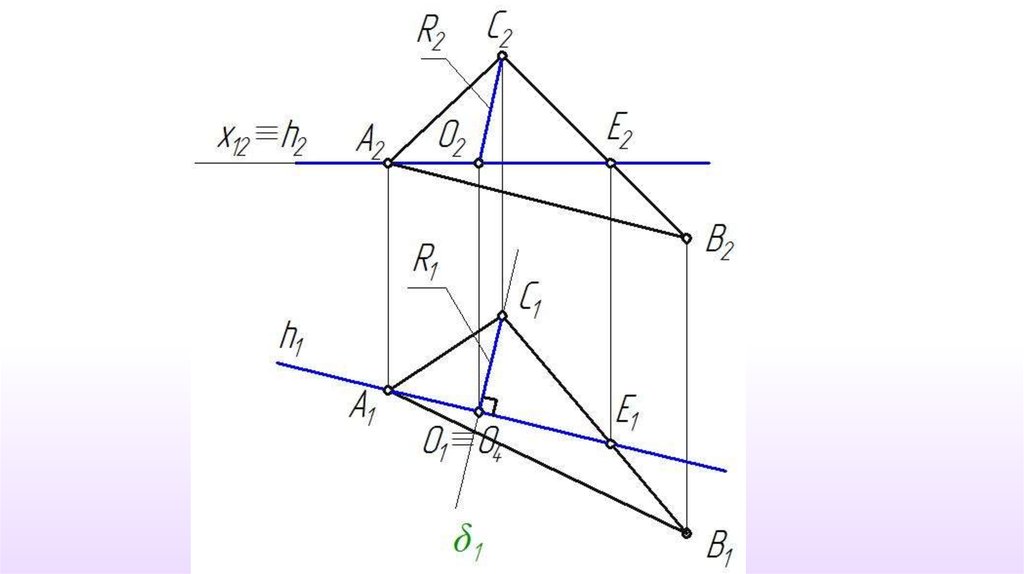
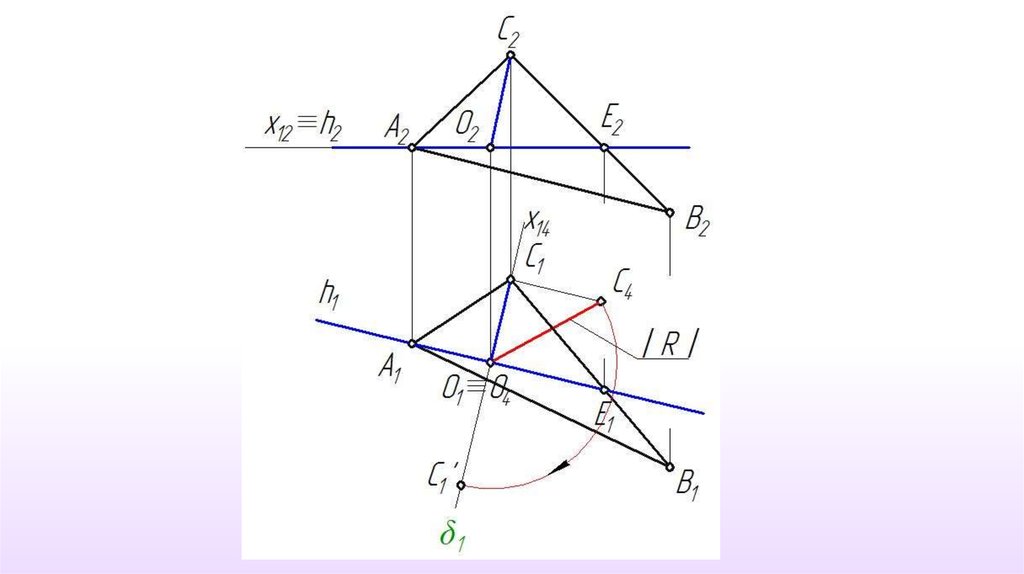
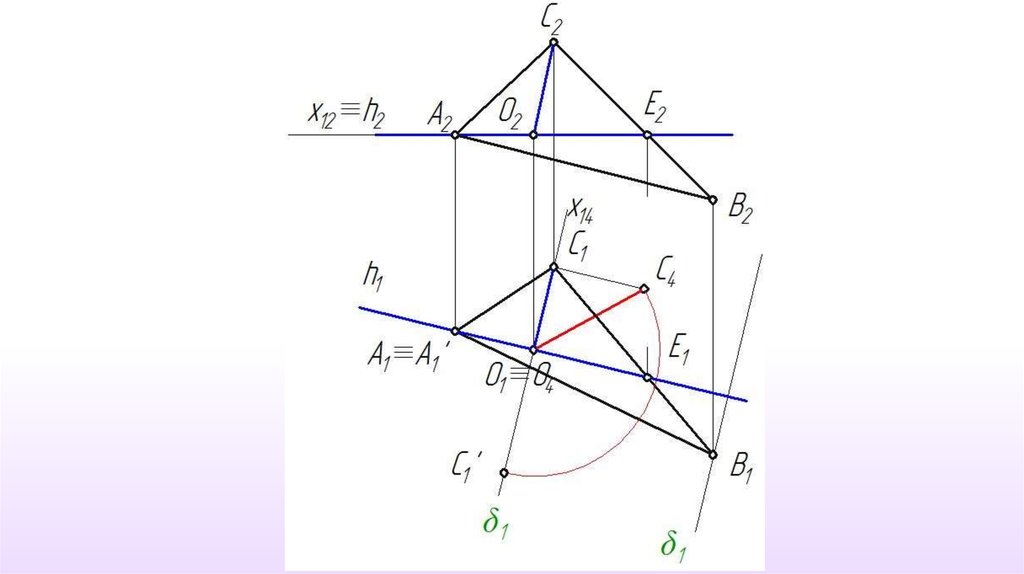
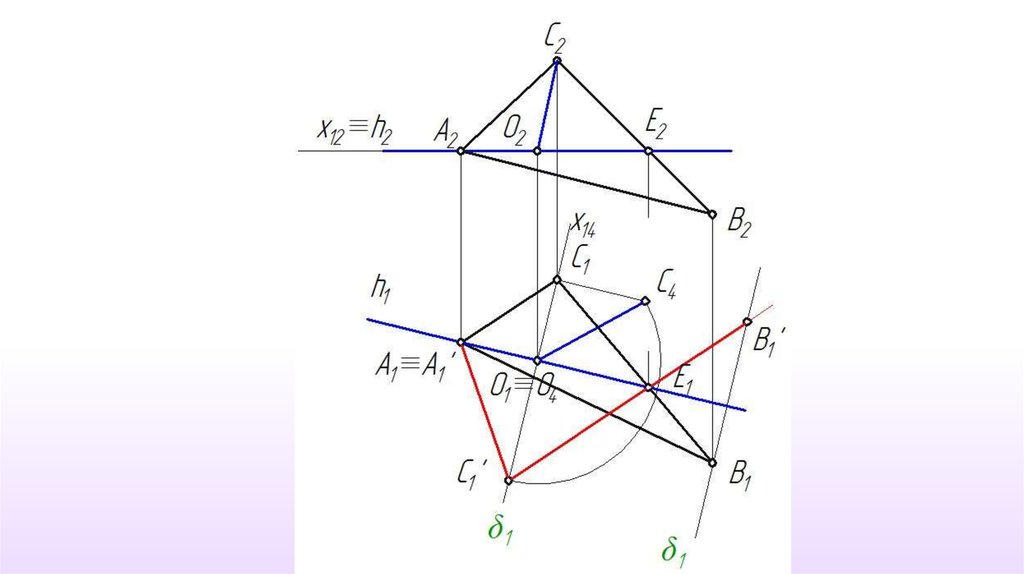
Решение задачи способом
вращения вокруг прямой уровня

26.

27.

28.

29.

30.

31.

32.

33.

34.

МЕТРИЧЕСКИЕ И КОНСТРУКТИВНЫЕ
ЗАДАЧИ

35.

Базовая
задача
Метрическая задача
№1
Определение истинной величины расстояния между двумя точками (длины
отрезка прямой).
Определение истинной величины угла наклона прямой к плоскости проекций.
№2
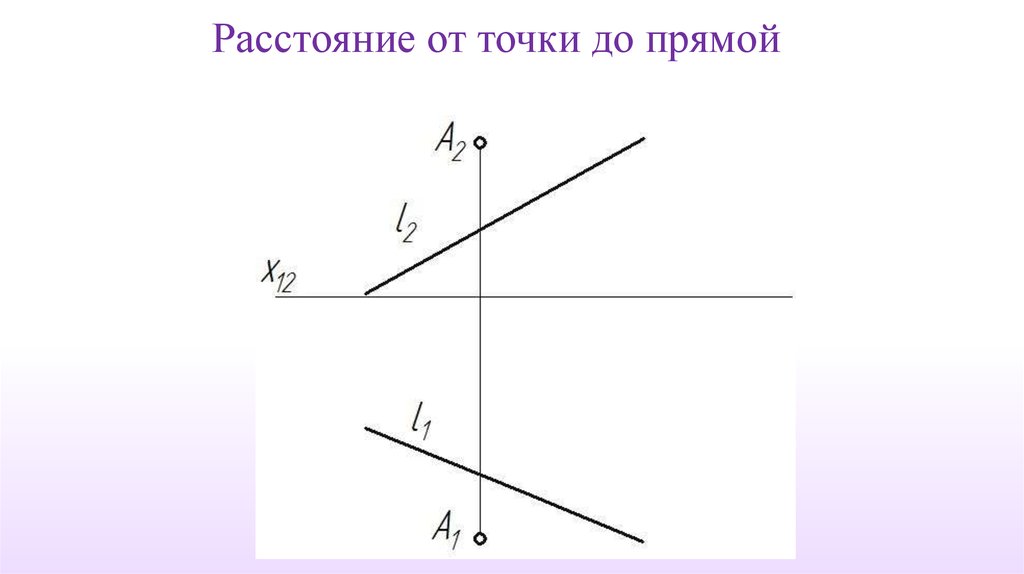
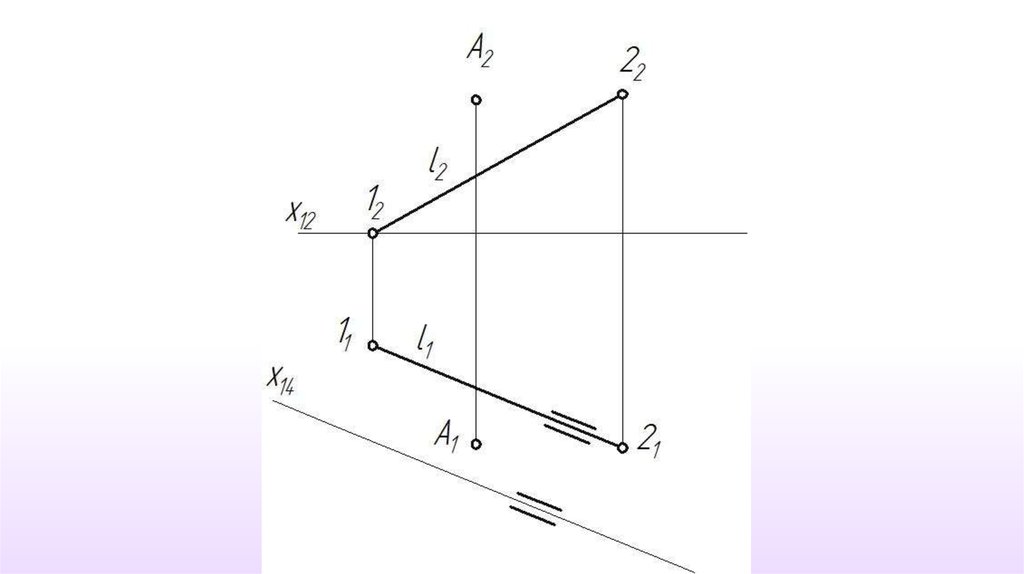
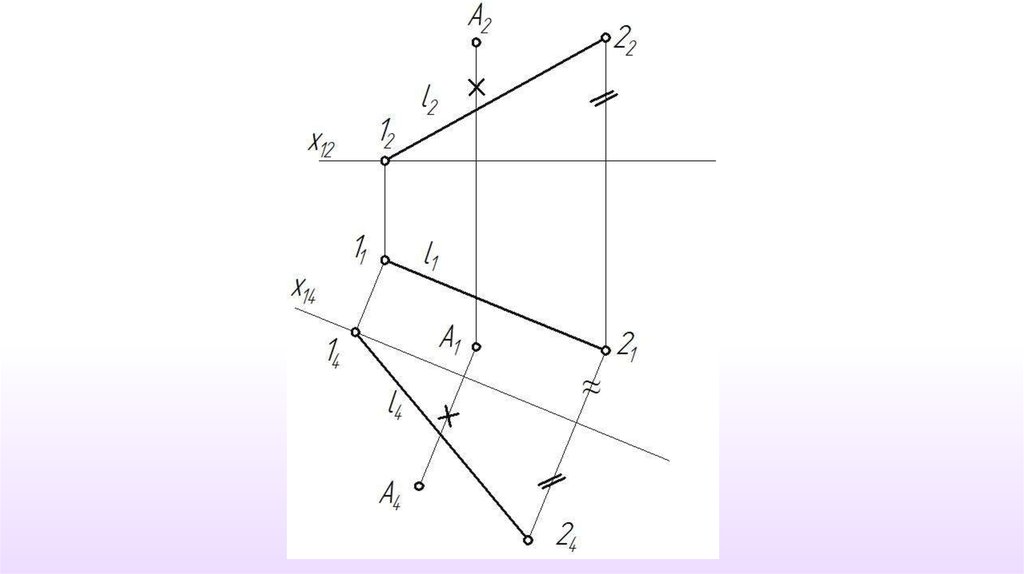
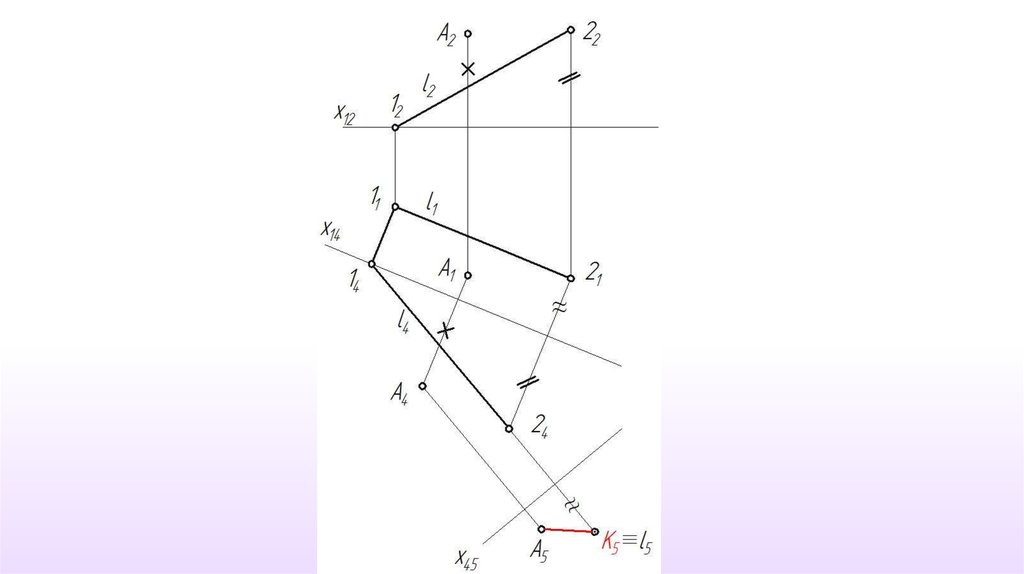
Определение истинной величины расстояния от точки до прямой.
Определение истинной величины расстояния между параллельными прямыми.
Определение истинной величины расстояния между скрещивающимися
прямыми.
Определение истинной величины двугранного угла.
№3
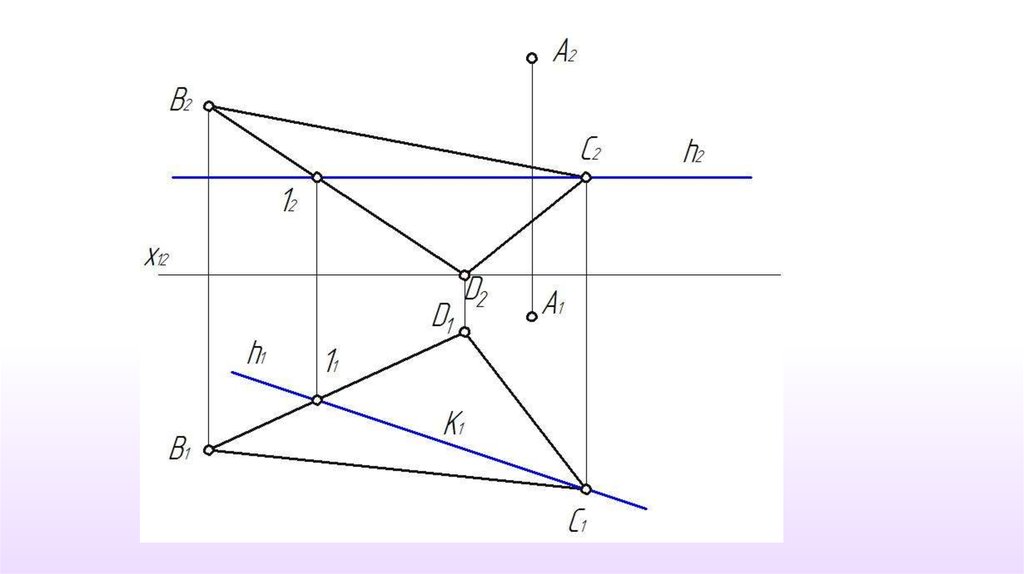
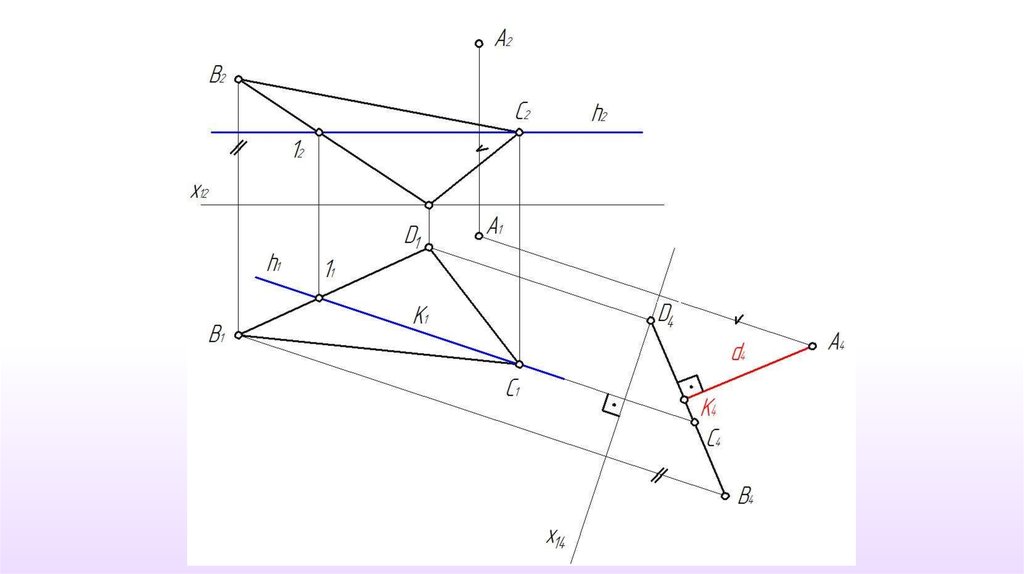
Определение истинной величины расстояния от точки до плоскости.
Определение истинной величины расстояния между параллельными
плоскостями.
Определение истинной величины угла наклона плоскости к плоскости проекций.
№4
Определение истинной величины угла между пересекающимися прямыми или
истинной величины плоской фигуры.
Определение истинной величины угла между скрещивающимися прямыми.
Определение истинной величины угла между прямой и плоскостью.
Определение истинной величины угла между двумя плоскостями.

36.

Расстояние от точки до прямой

37.

38.

39.

40.

41.

42.

43.

44.

Расстояние от точки до плоскости