Равнобедренный треугольник

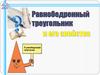
1. С

В
А
С
1
2

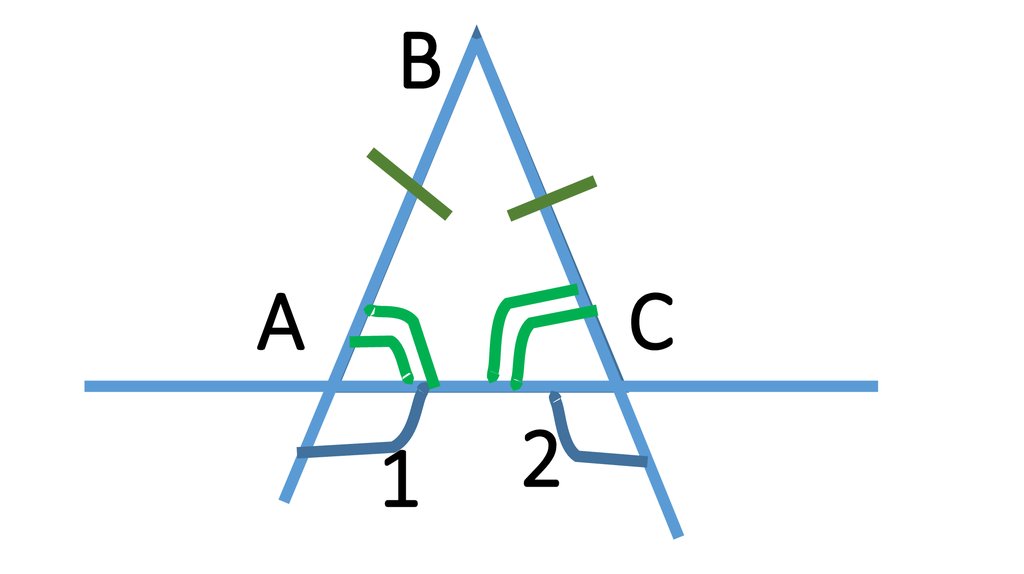
2. E

В
2
D
E

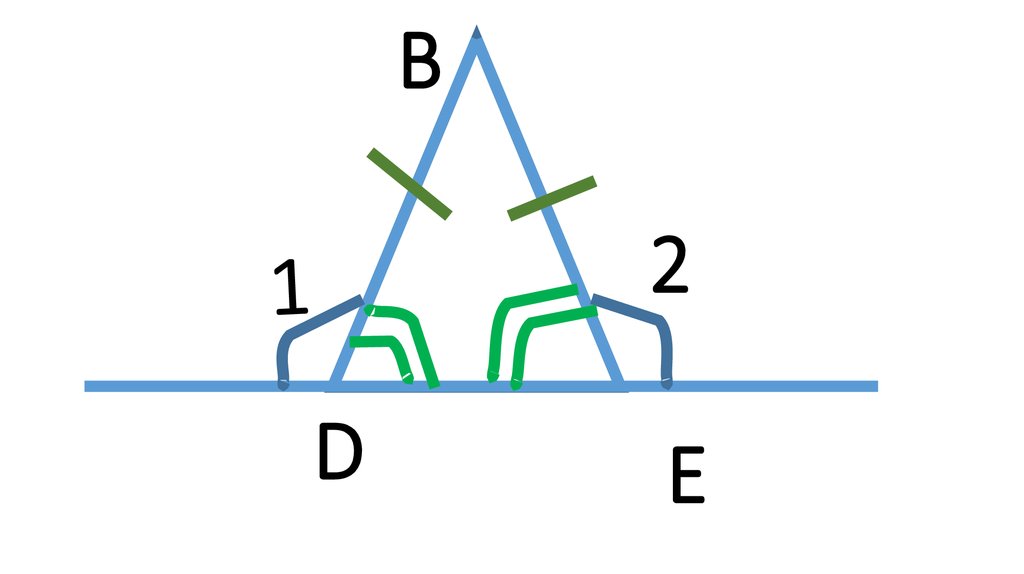
3. F

E
1
F
D
2

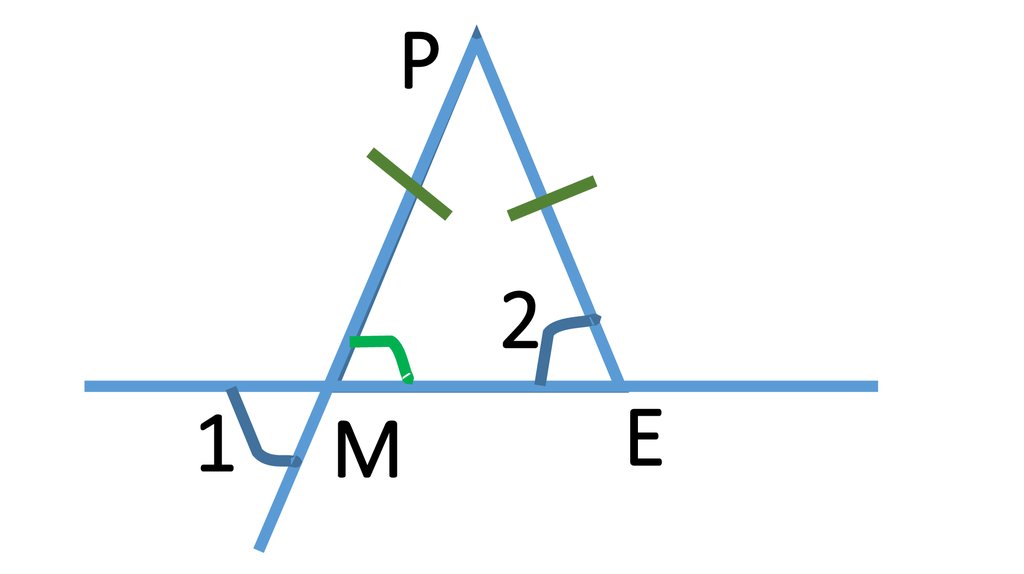
4. E

P
2
1
M
E

5.

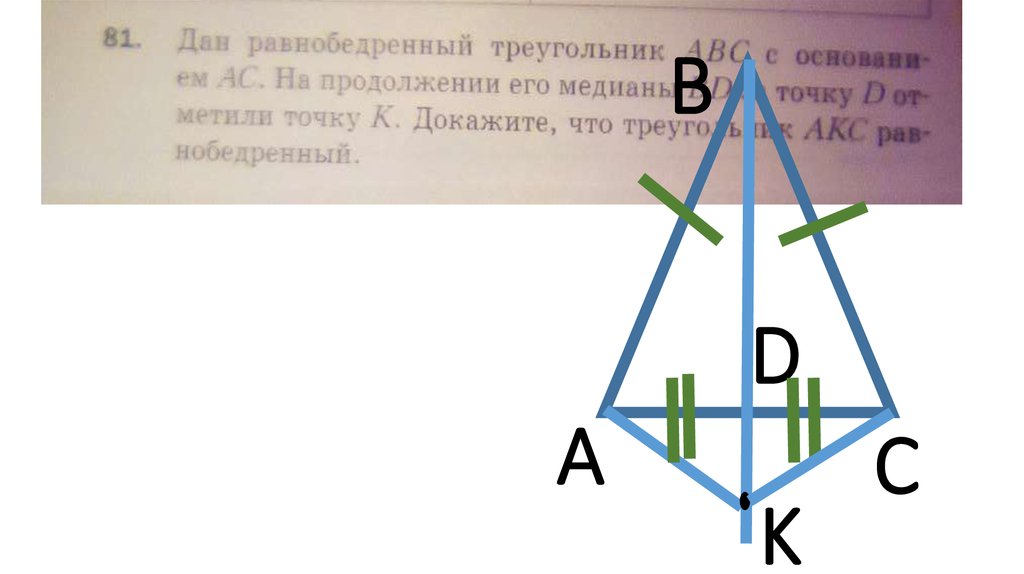
6.

B
D
A
K
C

7.

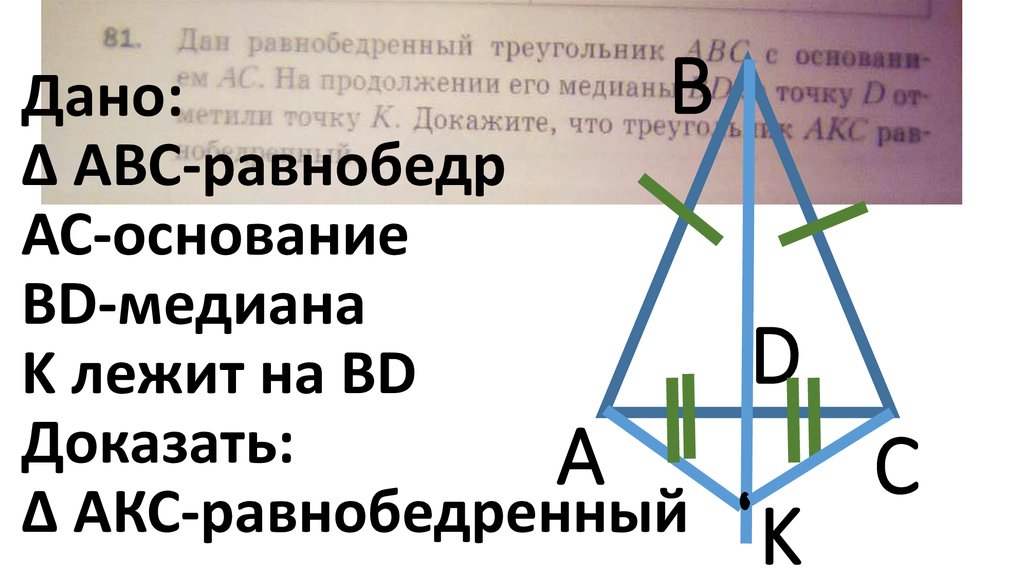
B
Дано:
∆ AВС-равнобедр
АС-основание
ВD-медиана
K лежит на BD
Доказать:
A
∆ АКС-равнобедренный
D
K
C

8.

Решение:
∆ AВС-равнобедр , значит, медиана BD
является высотой, тогда BD
перпендикулярна АС.
Значит, в ∆ АКС КD высота.
Т.к. AD=DC, то DK-медиана в ∆ АКС. Тогда
по признаку равнобедренного
треугольника(медиана является высотой)
имеем, что ∆ АКС-равнобедренный.
Что и требовалось доказать.

9.

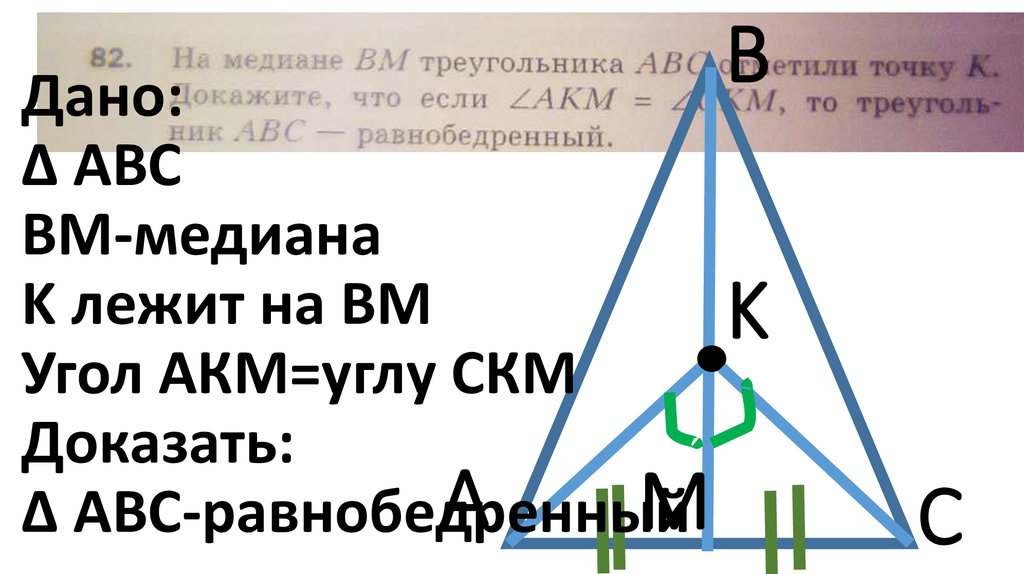
B
Дано:
∆ AВС
ВМ-медиана
K лежит на BМ
K
Угол АКМ=углу СКМ
Доказать:
A
М
∆ АВС-равнобедренный
C

10.

Решение:
ВМ-медиана треугольника
AВС, значит, АМ=МС.
В треугольнике АКС
отрезок КМ будет
медианой, а так как угол
АКМ равен углу СКМ, то
КМ является
A
биссектрисой.
B
K
М
C

11.

А по признаку
равнобедренного
треугольника: если медиана
является биссектрисой, то
треугольник
равнобедренный, т.е.
треугольник АКСравнобедренный.
Следовательно, КМ –высота
треугольника АКС(по св-ву),
а значит, ВМ высота и
треугольника АВС.
A
B
K
М
C

12.

Также ВМ-медиана
треугольника AВС. А по
признаку равнобедренного
треугольника: если медиана
является высотой, то
треугольник
равнобедренный. То есть
треугольник АВС –
равнобедренный, что и
требовалось доказать.
A
B
K
М
C