Похожие презентации:
Расчет параметров полнодоступных систем РИ с ожиданием
1.
ВОЕННАЯ АКАДЕМИЯ СВЯЗИ22 кафедра (сетей связи и систем коммутации)
Дисциплина: Сети связи и системы коммутации
Раздел 1: Теория распределения информации
Тема №3: Расчет полнодоступных систем с
ожиданием
Занятие №14: Расчет параметров полнодоступных
(практич.) систем РИ с ожиданием
2.
Учебные вопросы2
1. Выбор математической модели расчета систем с
ожиданием
2. Оценка параметров систем распределения
информации (практикум по расчету)
Литература
Зотов В.М. Основы теории распределения информации:
Учебное пособие. – СПб.: ВАС, 2013
2. Зотов В.М. Военная техника телефонной связи. Ч. 5.
Сборник задач и упражнений. – СПВВИУС, 1997.
3. Воробьев Л.В., Зотов В,М., Романенко П.Г., Щербина Л.П.
Расчет параметров систем распределения информации
методами теории телетрафика/Под ред. Л.П .Щербины. –
СПб., ВАС, 2010. 152 с.
1.
3.
Практикум по решению задач1. Выбор математической
систем с ожиданием
модели
3
расчета
4.
2-я формула Эрланга:ΕV ( Z )
pt p tож 0 1.
Z
1 (1 ΕV ( Z ))
V
6
5.
Формула Бухмана:p (tож τ) p (tож 0) e
1.
8
β V Z
6.
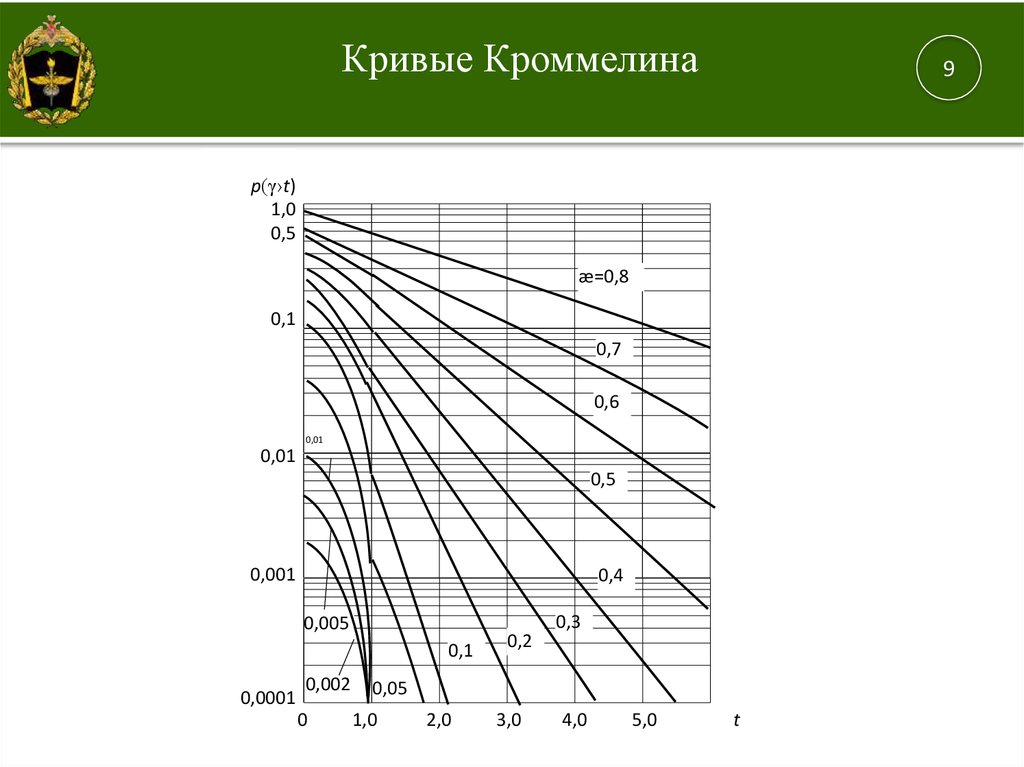
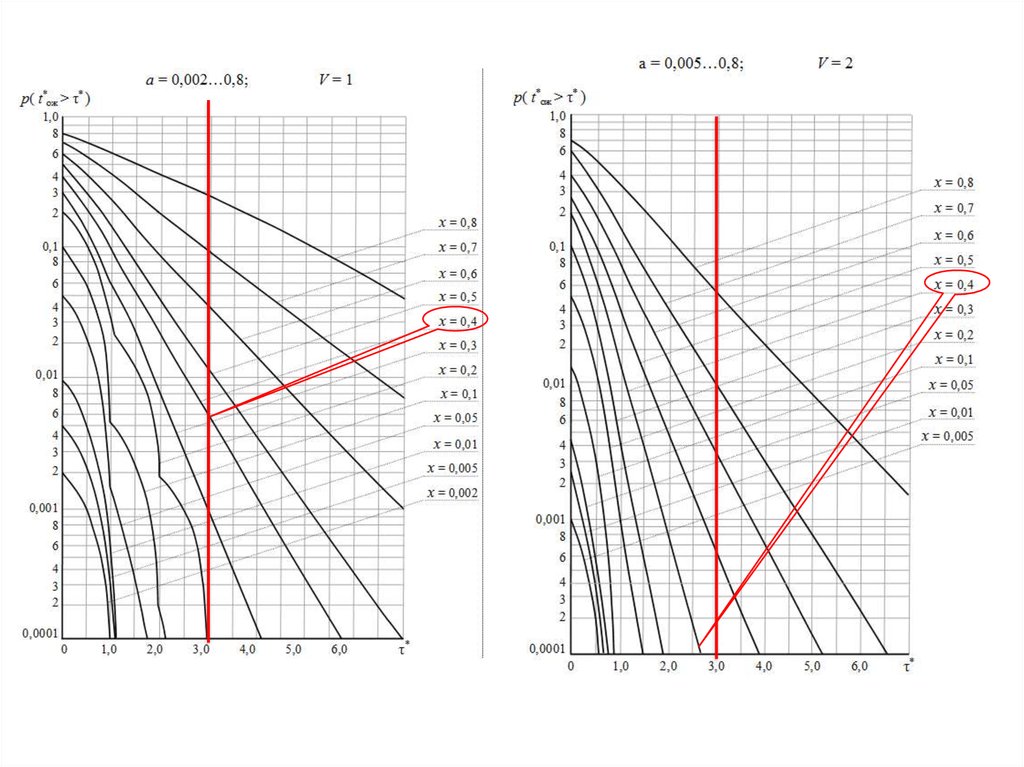
Кривые Кроммелина9
p(γ›t)
1,0
0,5
æ=0,8
0,1
0,7
1.
0,6
0,01
0,01
0,5
0,001
0,4
0,005
0,1
0,0001
0,002
0
0,2
0,3
0,05
1,0
2,0
3,0
4,0
5,0
t
7.
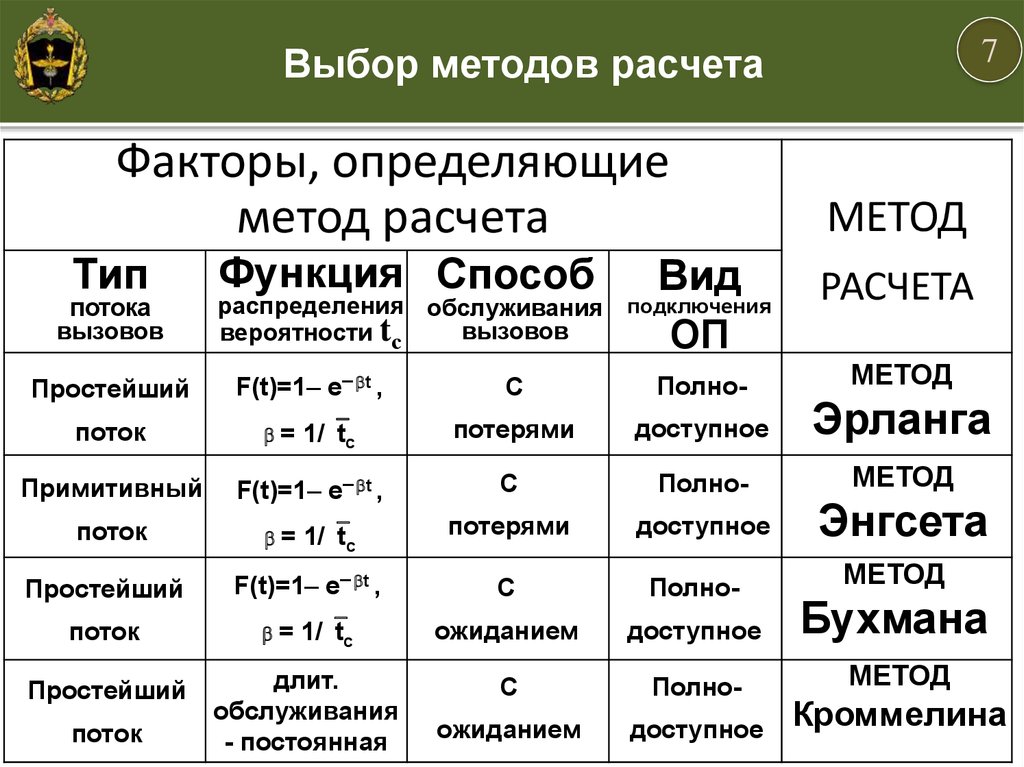
7Выбор методов расчета
Факторы, определяющие
метод расчета
Тип
потока
вызовов
Простейший
поток
Примитивный
поток
Простейший
поток
Простейший
поток
Функция Способ
Вид
распределения обслуживания подключения
вызовов
вероятности tс
МЕТОД
РАСЧЕТА
ОП
F(t)=1– e– t ,
= 1/ tс
F(t)=1– e– t ,
= 1/ tс
F(t)=1– e– t ,
= 1/ tс
длит.
обслуживания
- постоянная
МЕТОД
С
Полно-
потерями
доступное
Эрланга
С
Полно-
МЕТОД
потерями
доступное
Энгсета
МЕТОД
С
Полно-
ожиданием
доступное
Бухмана
С
Полно-
МЕТОД
ожиданием
доступное
Кроммелина
8.
Практикум по решению задач8
2. Оценка параметров систем распределения
информации (практикум по расчету)
9.
Практикум по решению задач9
Задача 1:
Определить качество обслуживания p( t > ) на ветви
из V=12 каналов при поступлении нагрузки Z=7,5 Эрл и
относительном времени ожидания Q=0,5.
Задача 2:
На
станции
имеется
V=18
каналов,
которые
обслуживают нагрузку Z=15 Эрл с качеством р (t > ) =
0,1. Определить допустимое время ожидания, если
средняя длительность занятия канала равна tс=5 мин.
10.
Практикум по решению задач10
Задача 3:
На
телефонной
станции
есть
возможность
ограничивать нагрузку на направление связи,
содержащее V =30 каналов путем лишения абонентов
права выхода на ТС ДС. Определить максимально
допустимое число абонентов, которым можно
предоставить это право чтобы обеспечить
качество обслуживания р(t >4 мин)=0.1, если среднее
числе вызовов в ЧНН от одного абонента са=1.25 и
среднее время занятия канала tс=4 мин.
11.
Практикум по решению задач11
Задача 4:
Однолинейная система с ожиданием обслуживает
поступающую нагрузку Z = 0,7 Эрл при постоянной
длительности занятия tc = 0,3 с. Допустимое время
ожидания в системе = 0,6 с. Определить долю
вызовов, попадающих на ожидание и долю вызовов,
ожидающих
обслуживания
сверх
допустимого
времени ожидания.
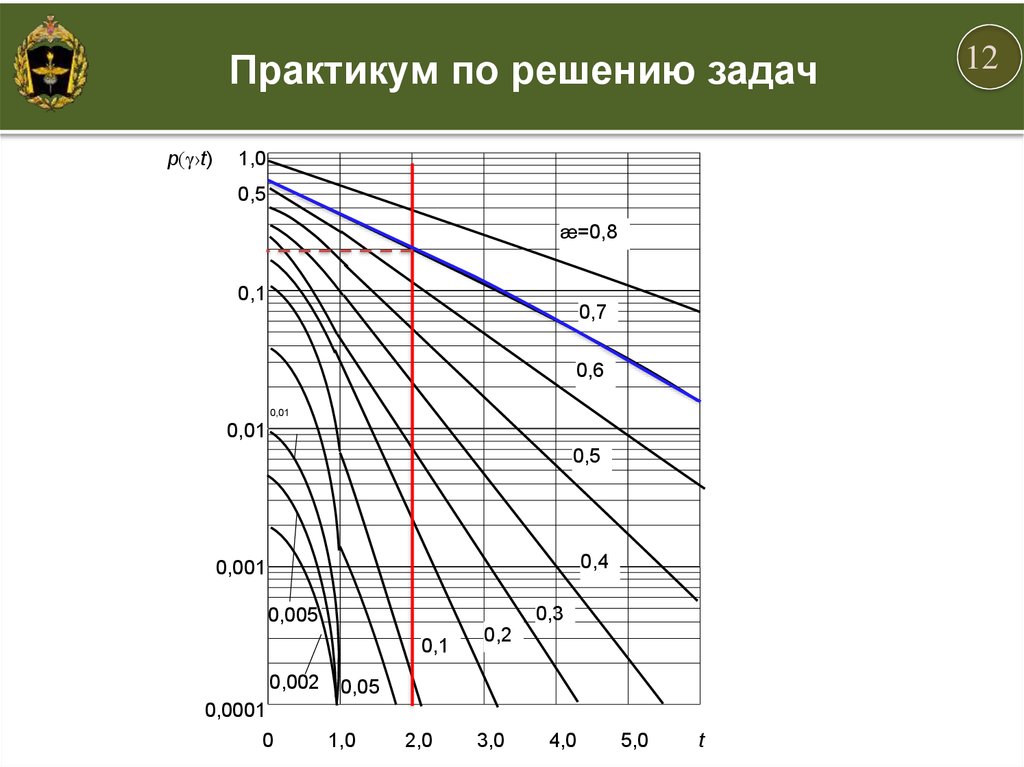
12.
Практикум по решению задачp(γ›t)
1,0
0,5
æ=0,8
0,1
0,7
0,6
0,01
0,01
0,5
0,4
0,001
0,3
0,005
0,1
0,002
0,2
0,05
0,0001
0
1,0
2,0
3,0
4,0
5,0
t
12
13.
Практикум по решению задач13
Задача 5.
Определить требуемое количество устройств
управления АТС при Z=0.4 Эрл, если известны
длительность занятия УУ tс= 20 мс, вероятность
ожидания обслуживания вызова Р( > t) = 0,001 и
допустимое время ожидания начала обслуживания =
60 мс
14.
15.
616.
14ЗАДАЧА 7
Направление связи, включающее 10 каналов и обслуживающее
поступающие вызовы с показателем р (tож >5 мин)=0,1 при
средней длительности занятия, равной 2,5 мин, переводится на
обслуживание с потерями. Определить качество обслуживания
при сохранении прежнего числа каналов в направлении. Какие
меры необходимо предпринять для обеспечения требуемого в
сети дальней связи качества обслуживания ?












 Информатика
Информатика