Плоскость. Определить положение плоскостей к плоскостям

1. Тема 2 Плоскость

2.

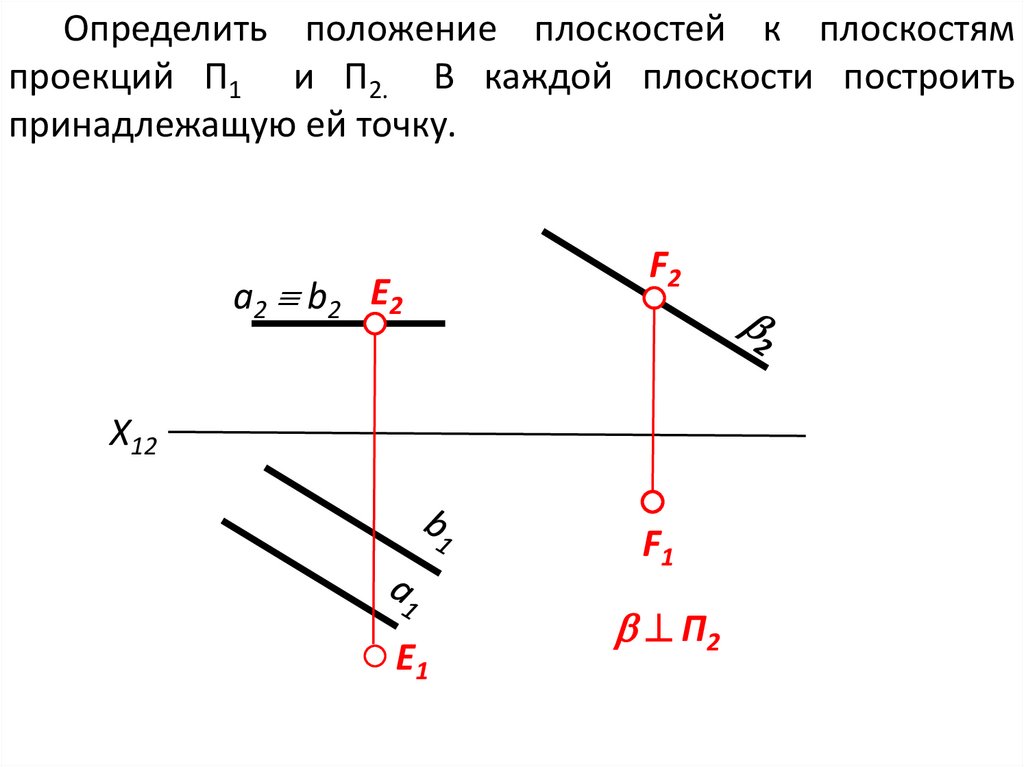
Определить положение плоскостей к плоскостям
проекций П1 и П2. В каждой плоскости построить
принадлежащую ей точку.
a2 b 2 E2
F2
X12
F1
E1
П2

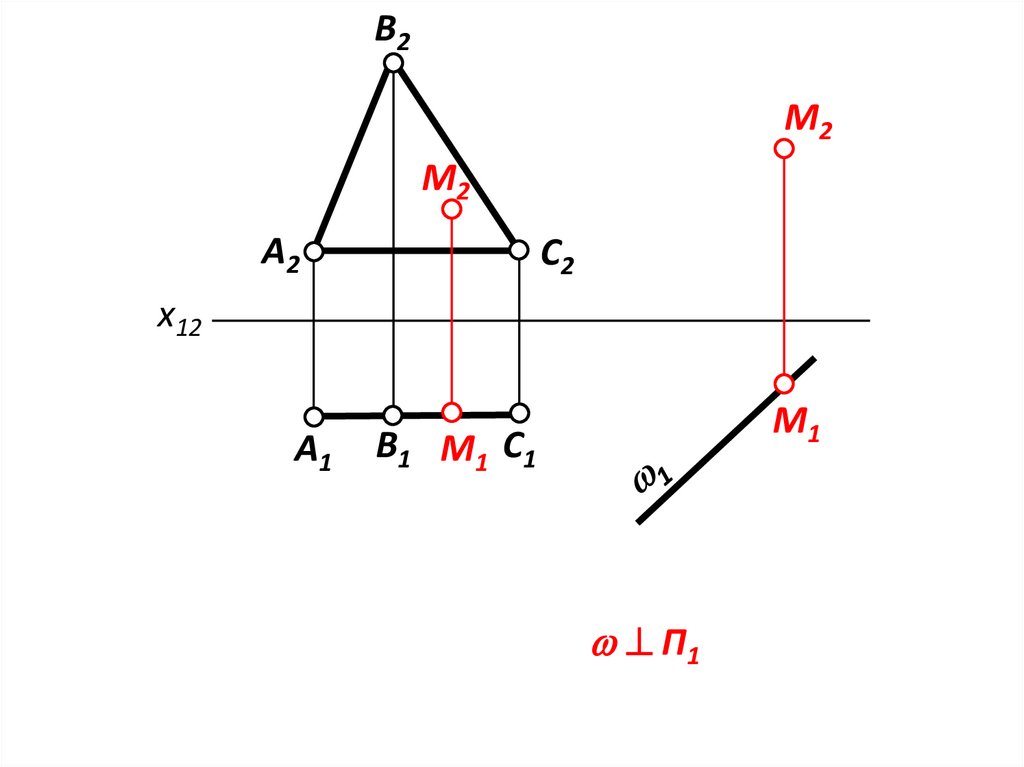
3.

B2
M2
M2
A2
C2
x12
A1
M1
B 1 M 1 C1
П1

4.

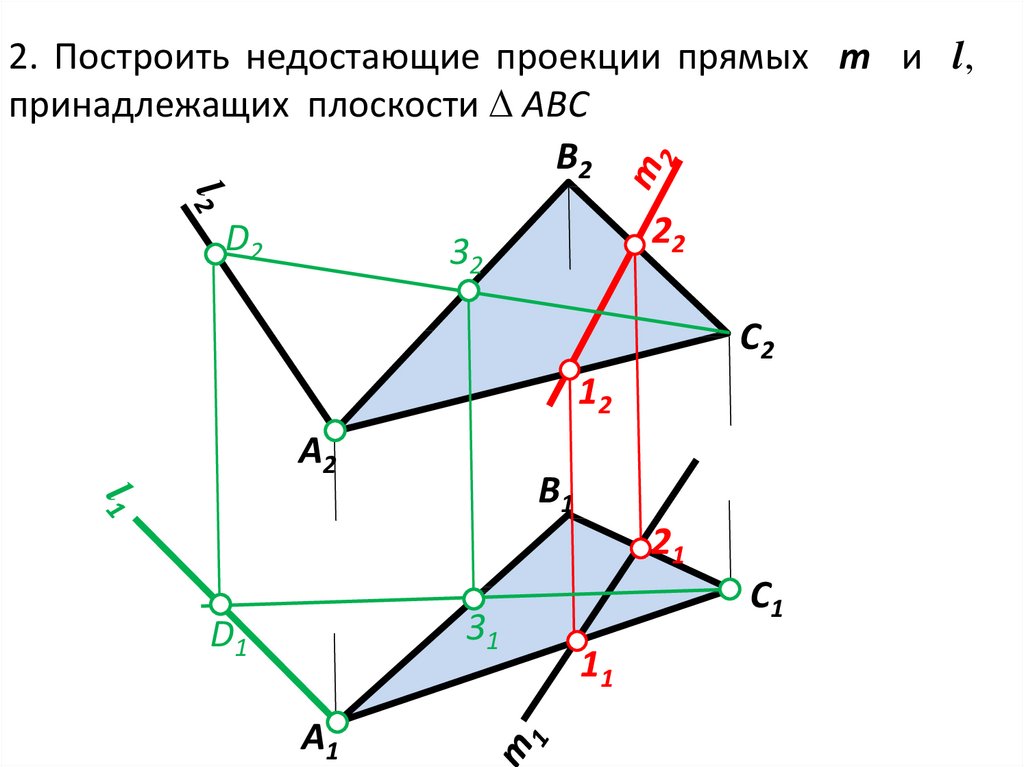
2. Построить недостающие проекции прямых m и l,
принадлежащих плоскости ABC
B2
D2
22
32
C2
12
A2
B1
21
31
D1
A1
C1
11

5.

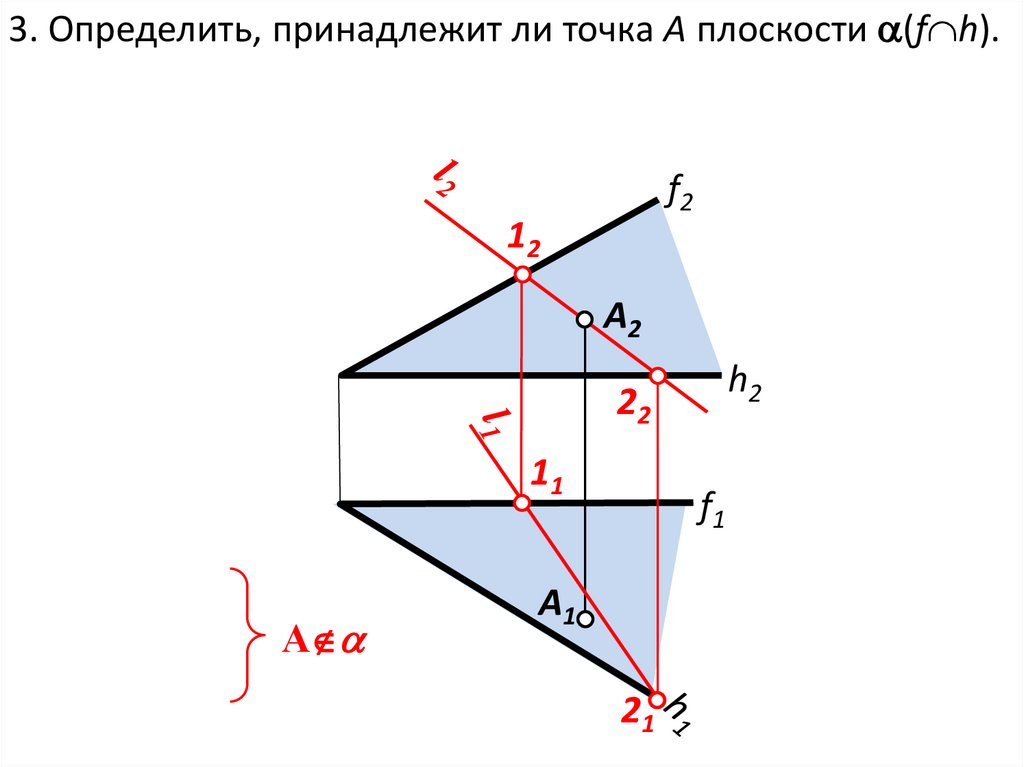
3. Определить, принадлежит ли точка А плоскости (f h).
f2
12
A2
h2
22
11
(f h)
l
А l
А
f1
A1
21

6.

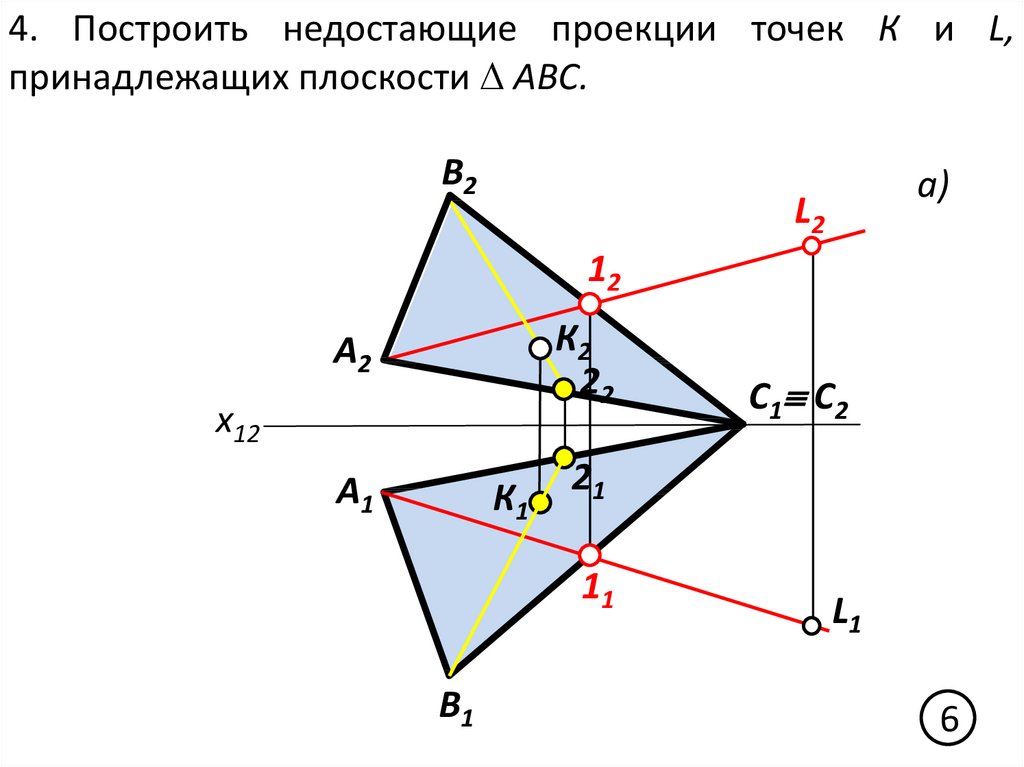
4. Построить недостающие проекции точек К и L,
принадлежащих плоскости АВС.
В2
a)
L2
12
A2
К2
22
A1
21
x12
К1
11
В1
С1 С2
L1
6

7.

5. Построить недостающие проекции точек А и В,
принадлежащих плоскости, заданной пересекающимися
прямыми f и h.
б)
A2
x12
f1 h2
12
B2
A1
B1
11
6

8.

7. Построить недостающую проекцию треугольника,
принадлежащего плоскости (f h).
В2
12
22
x12
а)
A2
f 1 h2
С2
21 11
A1
C1
В1
7

9.

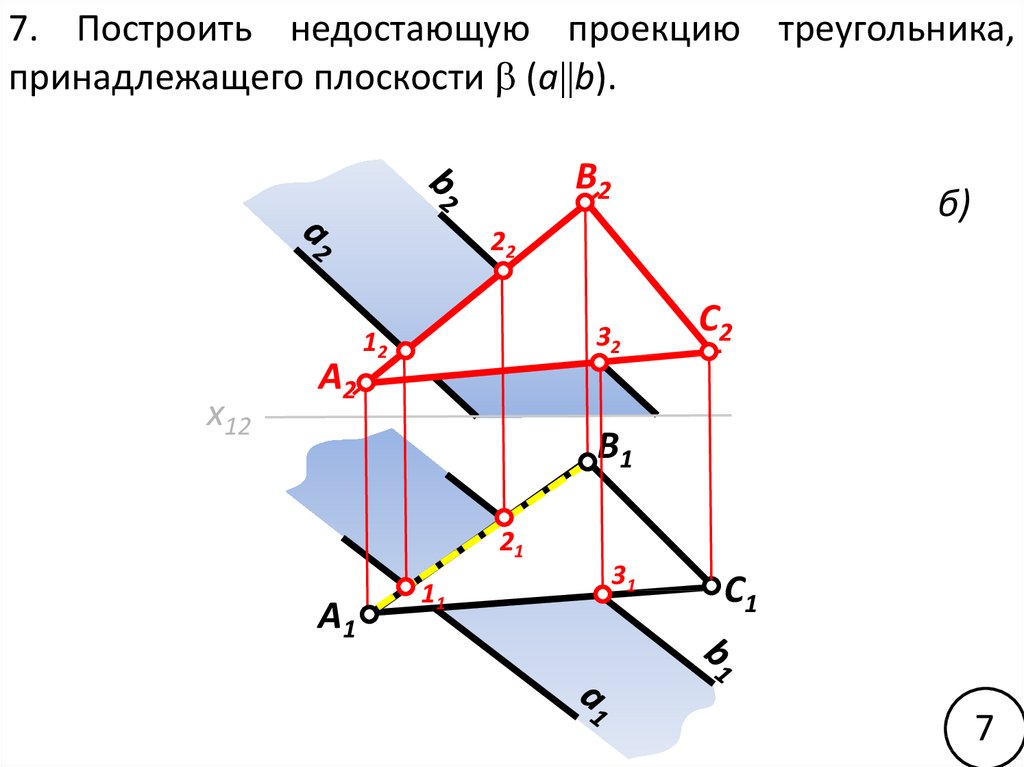
7. Построить недостающую проекцию треугольника,
принадлежащего плоскости (a b).
В2
б)
22
x12
A2
32
12
C2
В1
21
A1
11
31
C1
7

10. Тема 3 Пересечение прямой и плоскости Пересечение плоскостей

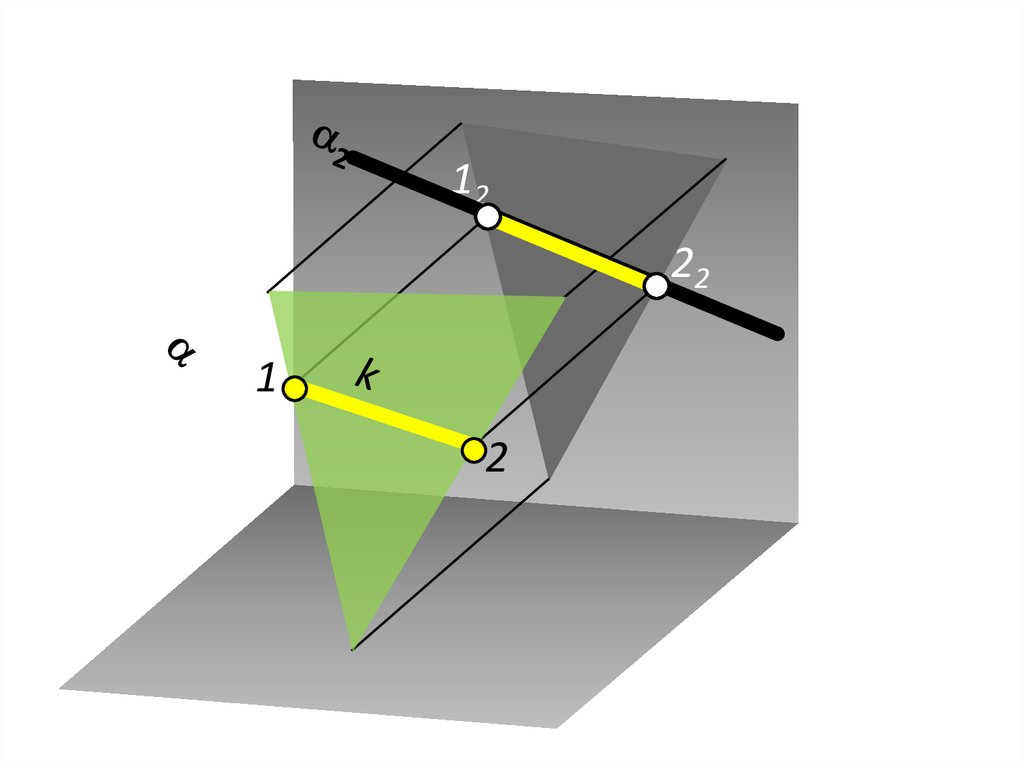
Пересечение плоскости общего
положения проецирующей
плоскостью

11.

12
22
1
2

12.

12
22
Линия пересечения плоскости
ОП с
плоскостью ЧП имеет одну из своих
проекций на одноименном задающем
x12 плоскости ЧП .
следе
A1
11
B1
21
C1

13.

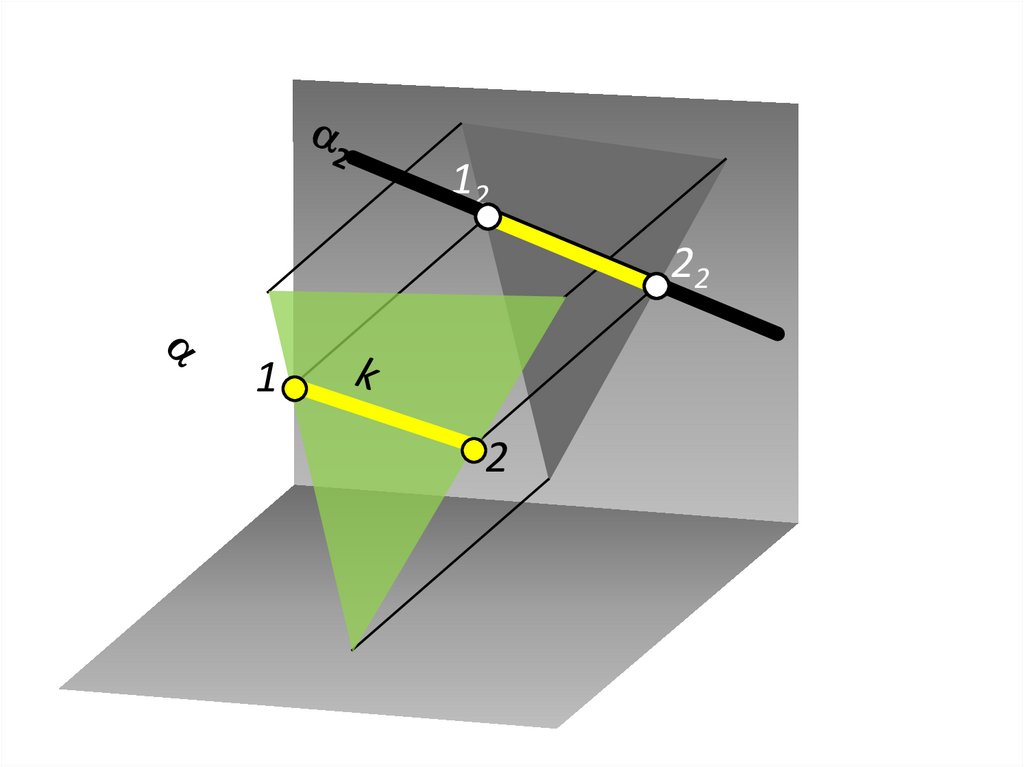
Пересечение прямой и плоскости
общего положения

14.

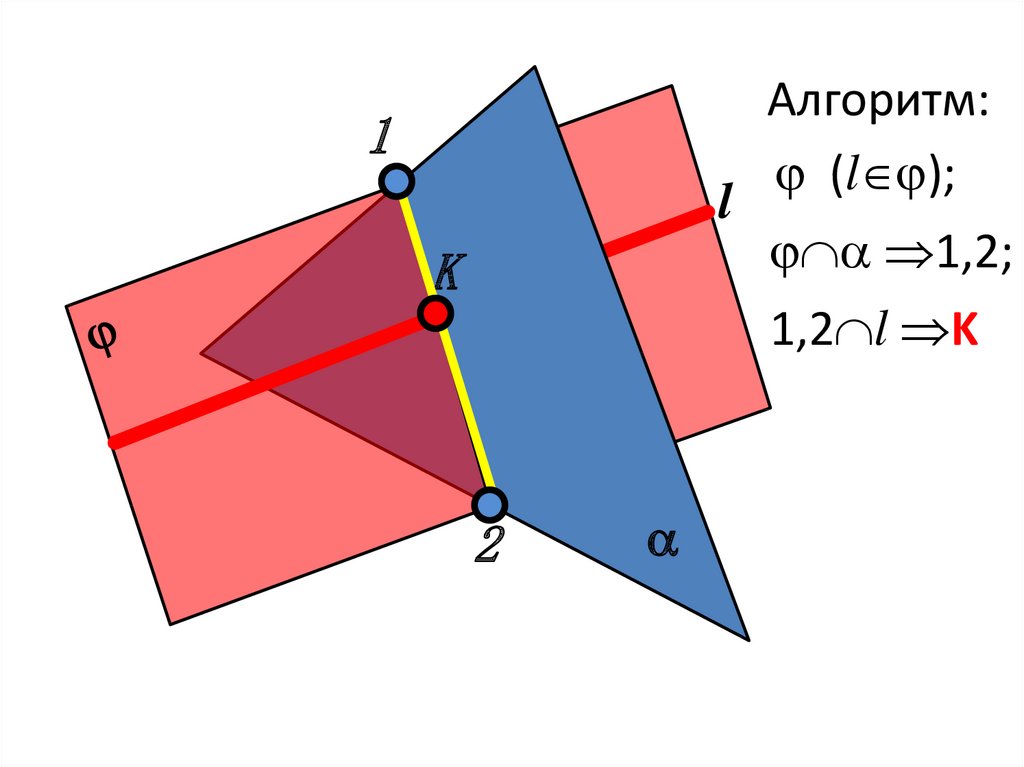
1
l
K
Алгоритм:
(l );
1,2;
1,2 l K
2

15.

1. Построить точку пересечения прямой l с плоскостью.
1
б)
K
12
K2
22
m
x12
l1
11
2
K1
21
1

16.

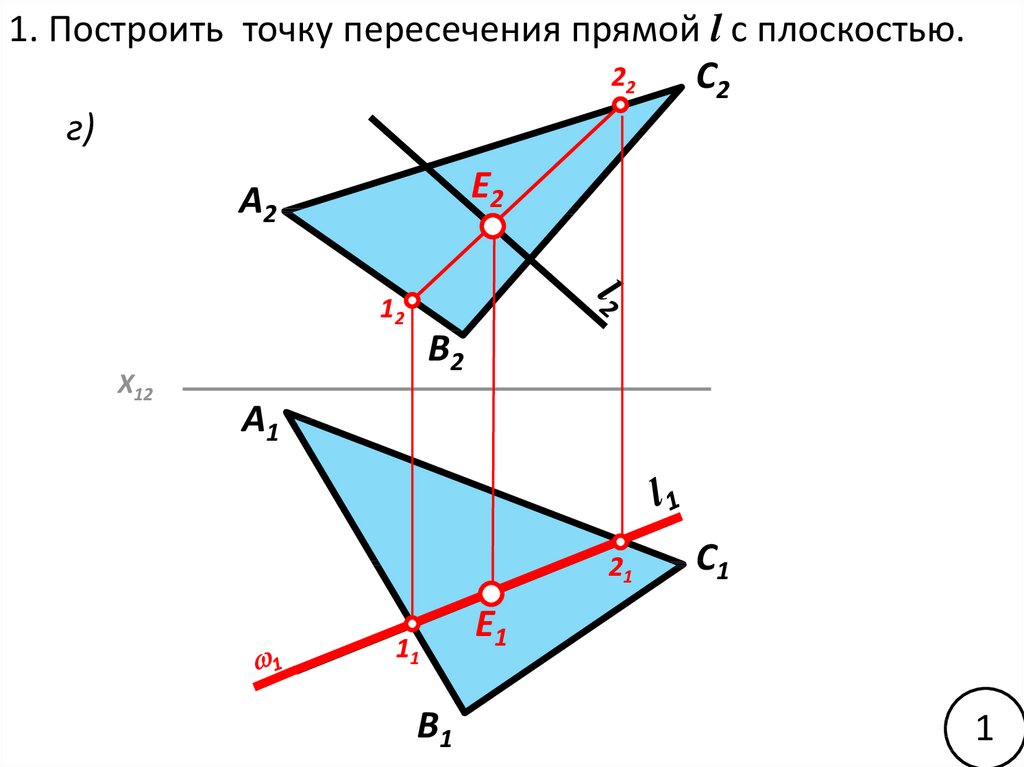
1. Построить точку пересечения прямой l с плоскостью.
22
C2
г)
E2
A
2
12
X12
В2
A1
21
11
В1
С1
E1
1

17.

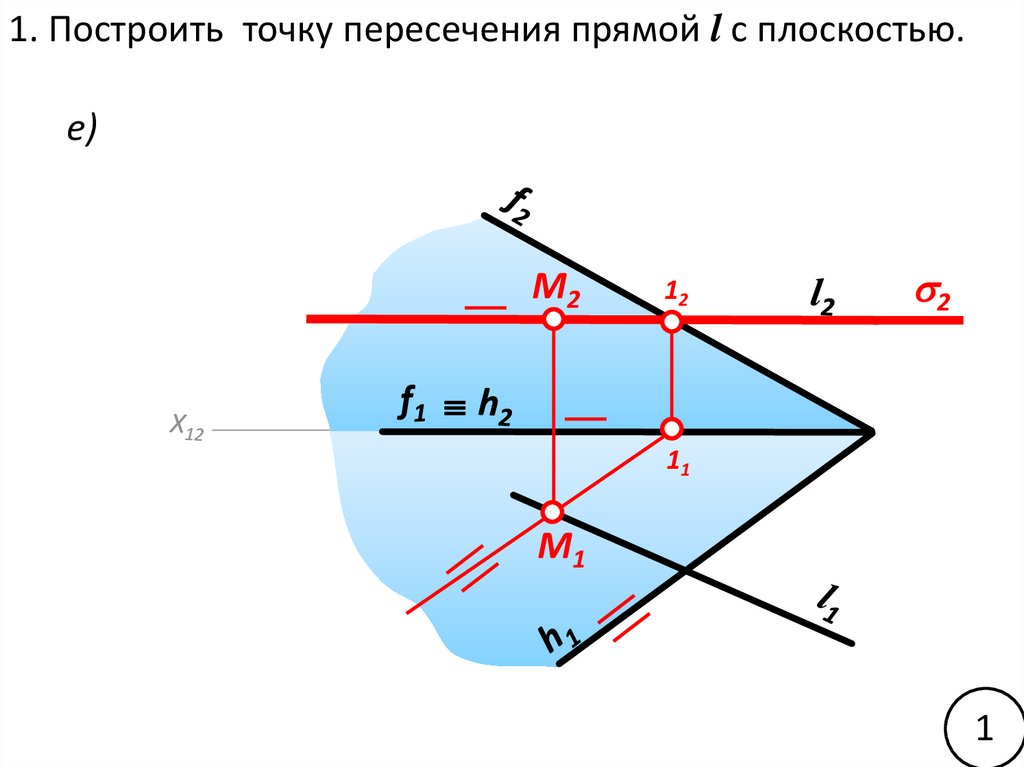
1. Построить точку пересечения прямой l с плоскостью.
е)
M2
12
2
11
M1
1

18.

Пересечение плоскости общего
положения с проецирующей
плоскостью

19.

12
22
1
2

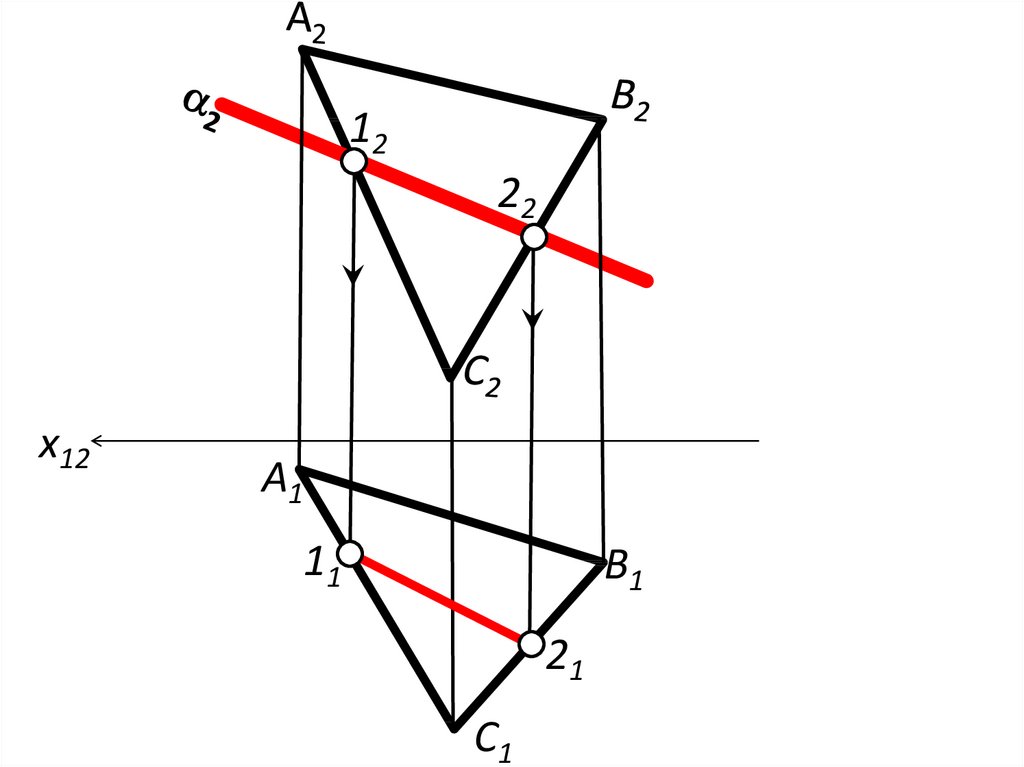
20.

12
22
x12
A1
11
B1
21
C1

21.

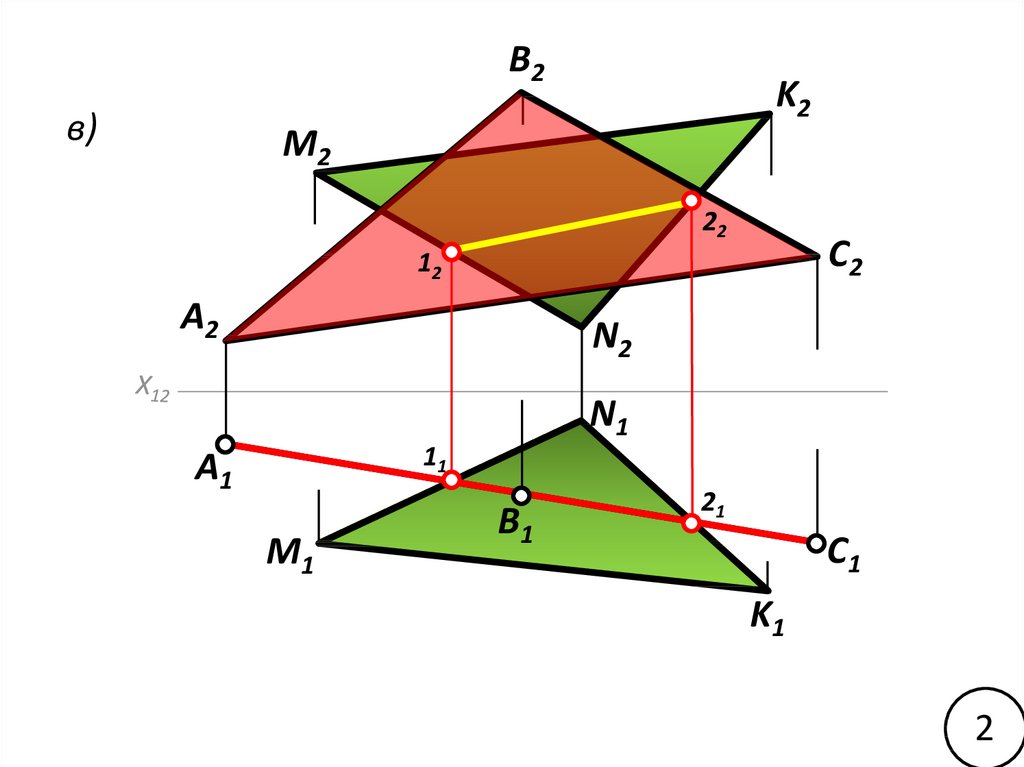
B2
в)
K2
M2
22
C2
12
A2
N2
N1
11
A1
M1
B1
21
C1
K1
2

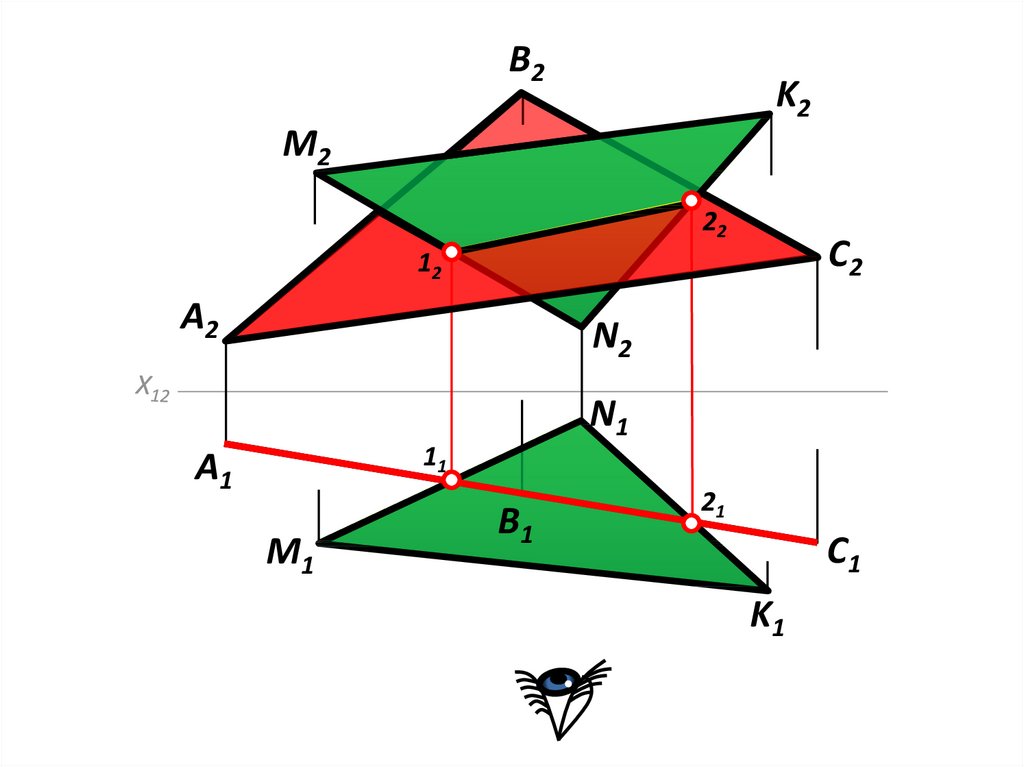
22.

B2
K2
M2
22
C2
12
A2
N2
N1
11
A1
M1
B1
21
C1
K1

23.

Пересечение плоскостей общего
положения

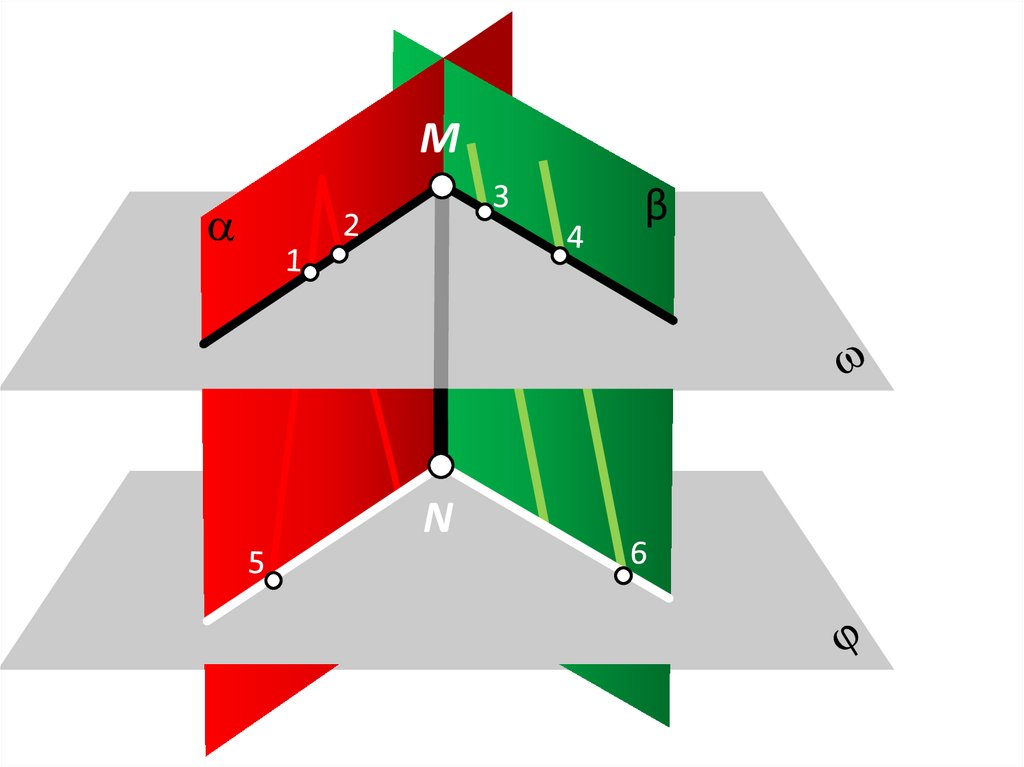
24.

M
β
N

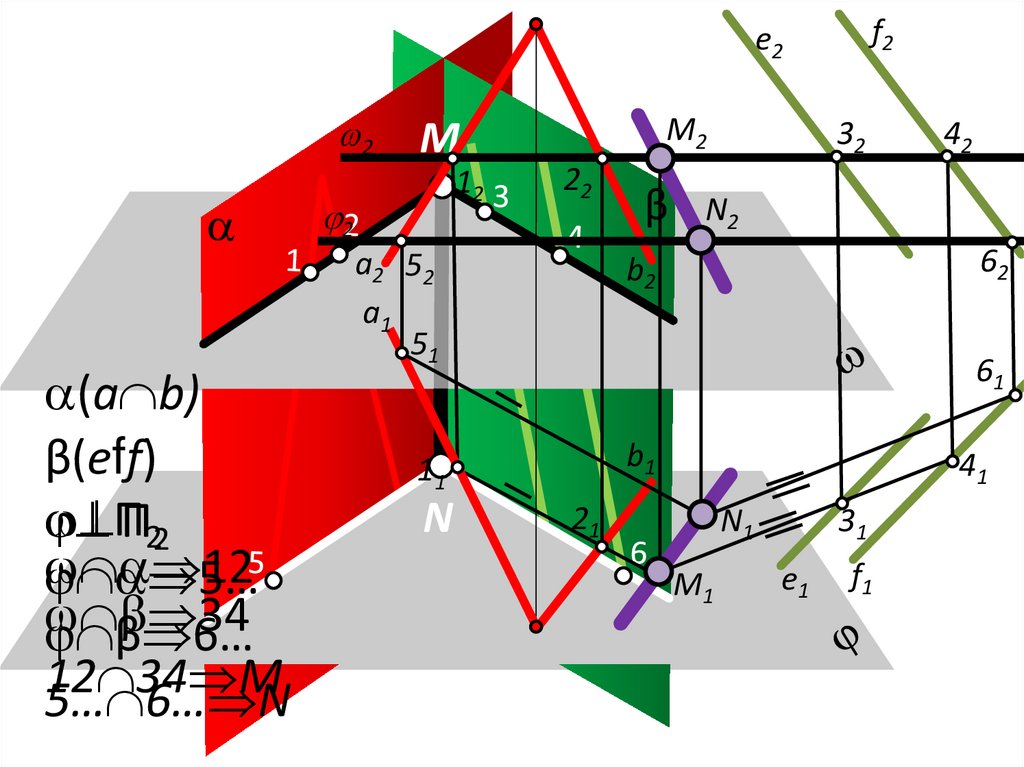
25.

f2
e2
2
12
2
(a b)
β(eff)
ПП22
12
5…
34
β 6…
12 34 M
5… 6… N
M2
M
22
β
a2 52
a1
51
b2
11
b1
N
32
42
N2
62
61
41
21
N1
M1
31
e1
f1

26.

2. Построить линию пересечения плоскостей
д)
A2
2
2
12
22
T2
B2
32
42
R2
41
11
C2
B1
A1
21
T1
31
C1
R1
2